یادآوری مقدماتی نظریه مجموعهها (۱) ویراست ۳.۹- ۱۳۹۴/۰۲/۰۱ - این متن ویرایش نهایی نشده است. بنابراین، میتواند دارای کاستی باشد.
- با توجه به راهنمایی علاقهمندان این متن در معرض ویرایش خواهد بود.
- بسی سپاس اگر خطاها و کاستیها یادآوری شود.ctologic@gmail.com
یادآوری نظریه مجموعهها, Reminder of Set Theory۱ مقدمه مجموعهها و درواقع "نظریه مجموعهها" یک نظریه استنتاجی ➥ [*]- در ادامه یادداشتهای منطق، تئوری استنتاجی و نیز دستگاههای اصل موضوعی مورد ملاحظه قرار خواهند گرفت. است که بهوسیله جرج کانتور بنیاد گردیده. ریاضیدانان با چندین رهیافت این نظریه را بیان میکنند. ازجمله آنها نظریه طبیعی مجموعهها ➥ P. R. Halmos, "Naive Set Theory", Springer, 1974 -1998. است که در آن بهرهوری از زبان طبیعی حداکثری است. اما بیان گوهری آن توسط دستگاههای اصل موضوعی است. ازجمله دستگاههای اصل موضوعی مجموعهها، دستگاه موسوم به زیملو-فرانکل / Zermelo-Fraenkel با کوتاه شده ZF است. این دستگاه به شمول اصلی موسوم به اصل انتخاب / Axiom of Choice (که در ادامه با همین عنوان آن را خواهیم دید) با کوتهسازی ZFC و گاهی ZF+C، بنیاد ریاضیات جاری است. دستگاه دیگر موسوم به Neumann-Bernays-Godel با کوتهسازی NBG است. دستگاه NBG و ZFC بسیار شبیه و همساز هستند. تفاوت عمده در وجود چیزی بنام "کلاس" در دستگاه NBG است که مجموعه بهعنوان گونهای از آن معرفی میگردد. در بند ۲.۱، کلاس و مجموعه، کمی بیشتر در این باره توضیح خواهد آمد. آنچه در پی و قسمتهای بعد خواهد آمد صرفاً معرفی بعضی واژگان این نظریه است که در ادامه نگاه نزدیکتر به منطق (و نیز رایانش) به آنها نیازمندیم. علت این نیاز ازجمله دقت و ژرفی، درعینحال سادگی آنهاست و اگر بتوانیم آنها را بجا به کار ببریم، هر بار از چندین و چند صفحه توضیحات، که خود میتوانند باعث ابهام و چندمعنایی در کلام شود، جلوگیری خواهد شد.
۱.۱ مجموعه و عضویتداستان را از فرد معینی بنام پرویز آغاز کنیم که هرروز صبح فرزند خود را از مسیر مشخص به مدرسه میرساند. وی در راه مدرسه هرروز چیزهای ثابتی، مانند تابلوی یک دندانپزشک، یک کیوسک مطبوعاتی، ماشین پارک شده مدیر مدرسه, خدمتگزار مدرسه، باجه تلفن و مانند آنها را میبیند. وی میتواند برای همه این چیزها یک نام انتخاب و ازآنپس با آن نام از آنها یاد کند. فرض کنیم نام انتخابی وی "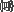 "باشد. اکنون میتوان گفت "باشد. اکنون میتوان گفت 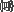 نام یک مجموعه است و تعریف نام یک مجموعه است و تعریف 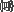 (تعریف مجموعه (تعریف مجموعه 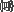 و نه تعریف مجموعه) میتواند "چیزهایی که پرویز در مسیر روزانه رساندن فرزند خود به مدرسه میبیند" باشد. به هر یک از این چیزها گفته که یک عضو و نه تعریف مجموعه) میتواند "چیزهایی که پرویز در مسیر روزانه رساندن فرزند خود به مدرسه میبیند" باشد. به هر یک از این چیزها گفته که یک عضو 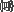 هستند [یا عنصر هستند [یا عنصر 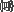 هستند یا در هستند یا در 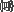 هستند، یا تعلق به هستند، یا تعلق به 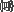 دارند.] دارند.] در متونی که از زبان ریاضی برای گویایی و دقت بهره میبرند، عبارتهایی کموبیش مثل "فرض کنید ∑ یک مجموعه باشد ..." بسیار بکار میرود. در این موارد، اول و مهمترین چیز این است که عناصری قرار است در میدان بحث بیایند که ازجمله عضو ∑ (یعنی عضو یک مجموعه) خواهند بود و بنابراین نقش اول آنها بهعنوان عضو مجموعه نام دادهشدهای خواهد بود. اینکه این عناصر چه هستند یا اصلاً وجود دارند، مسئله بعد است.
۲.۱ کلاس و مجموعهدر بیشتر متون مقدماتی تا متوسط منظور از رده یا کلاس [طبقه / Class] همان مجموعه است؛ با این اشاره ضمنی که اعضای آن خود هریک نام (یا نماینده) مجموعههای از پیش معینی ممکن است باشند، یا اعضای آن اعضای یک مجموعه گستردهتر هستند ولی تأکید بر ویژگی یا ویژگیهای مشخصی از اعضای این مجموعه که ممکن است همه اعضای آن مجموعه گستردهتر دارای این ویژگی(ها) نباشند. اما در سطح فنیتر (برای مثال، در دستگاه NBG که در بند ۱.۱ آمد)، "کلاس" یک چیز ابتدایی (تعریف نشده) است. در این دستگاه علاوه بر کلاس، "∈" نیز یک تعریف نشده دیگر است و فقط هم همین دو تعریف نشده هستند. فرض کنید C۱ و C۲ کلاس باشند، آنگاه مینویسیم: C۱∈C۲و به زبان فارسی میخوانیم: C۱ عضو C۲ است (یا C۱ به C۲ تعلق دارد، یا C۱ در C۲ است و مانند آنها). در این عالم (یعنی عالم کلاسها) که فقط از کلاس ساخته شده، کلاس ها را در دو دسته متمایز جای میدهند: ۱- کلاس سره: کلاسی که عضو هیچ کلاسی نیست. ۲- مجموعه: کلاسی که عضو بعض کلاس است [به چنین کلاس عنصر هم گفته میشود.] بنابراین، هر مجموعه کلاس است ولی همه کلاسها مجموعه نیستد. بهعبارتدیگر، بعضی کلاسها (کلاسهای سره) گستردهتر از آناند تا مجموعه باشند. بهعنوان مثال، کلاس همه مجموعهها یک کلاس سره است. در ادامه در بند ۷.۱ نمایاندن مجموعه (پارادوکس راسل) توضیح بیشتر خواهد آمد. دقیق و مشروح دستگاه NBG را میتوان در: Elliott Mendelson; "Introduction to Mathematical Logic"; Chapman & Hall, 1997; (فصل ۴: نظریه اصل موضوعی مجموعهها) یافت.
۳.۱ تساوی دو مجموعه: دو مجموعه مساوی هستند اگر و فقط اگر عضوی دریکی نباشد که در دیگری باشد. هر مجموعه با خودش مساوی است و بعلاوه اگر مجموعه A مساوی مجموعه B باشد(یعنی، A=B) آنگاه B نیز مساوی A است(یعنی، B=A)؛ همچنین، اگر A مساوی B و A مساوی C باشد آنگاه B مساوی C است.
۴.۱ مجموعه تهی:گاهی صحبت از چیزهایی از طریق وصف آنها میکنیم و از آنها بهعنوان همه اعضای یک گردآورده یاد میکنیم. اگر نشان دهیم جواب به پرسش وجود هر شئ در این گردآورده قطعاً منفی است (یعنی، هیچ شئ مطابق آن وصف وجود ندارد)، آنگاه مجموعهای داریم که خالی/تهی است. برای مثال اگر وصف اعضای گردآوردهای، به فرض ۰، "اعداد صحیح مضرب ۳ بین ۶ و ۹" باشد، آنگاه مقدار ارزش گزاره "هر عنصر ۰ کوچکتر از ۹ و بزرگتر از ۶ است" درست ولی پاسخ پرسش پیشتر گفته منفی است؛ بنابراین ۰ میتواند یک مجموعه و نیز یک مجموعه تهی باشد. بنابراین، چنین نیست که همه مجموعهها عضو داشته باشند. از تساوی مجموعهها میتوان نتیجه گرفت؛ همه مجموعههای تهی مساویاند و میتوان نشان معروف ∅ را به آن داد و از همه آنها با ∅ یادکرد.
۵.۱ زیرمجموعه:فرض کرده A و B دو مجموعه باشند، A را زیرمجموعه B گویند (و مینویسند: A⊂B) اگر و فقط اگر عضوی نباشد که در A باشد ولی در B نباشد. فیالبداهه مجموعه تهی زیرمجموعه هر مجموعهای است و هر مجموعه زیرمجموعه خودش است. بنابراین یک مجموعه تهی چندان هم بیچیز نیست و یک زیرمجموعه دارد. آشکار است که، اگر دو مجموعه زیرمجموعه هم باشند آنگاه آن دو مجموعه مساویاند و نیز وارون آن. بنابراین: (A⊂B) & (B⊂A) ⇔ A=B.
۶.۱ زیرمجموعه سره و ناسره:گیریم؛ A⊂B. به A یک زیرمجموعه سره B میگویند وقتی عضوی در B هست که در A نیست. بنابراین، ∅ زیرمجموعه سره همه مجموعههای ناتهی است و همینطور هر مجموعه زیرمجموعه ناسره خود است. از واژه "سره" در ریاضی کم استفاده نمیشود. برای مثال مقسومعلیه سره یک عدد صحیح باید غیر خود آن عدد باشد و همینطور طبقه/کلاس سره که در بالا دیدیم.
۷.۱ نمایاندن مجموعه معمولاً یک مجموعه خاص با بیان خاصیت/ویژگی/property اعضایش (تعریف مفهومی) یا با قرار دادن عضوها یا نشانه ویژه عضوها درون یک جفت آکولاد تعریف میشود(تعریف مصداقی/نمایشی). [البته نه هر خاصیتی-به پارادوکس راسل که در ادامه است توجه نمایید.] مجموعه تهی را با { } نمایش، همچنین عضویت(تعلق) و زیرمجموعه بودن ر به ترتیب با نمادهای '∈' و '⊂' نشان میدهند. معمولاً بهجای آنکه بگویند: چنین نیست که x(شیئی) متعلق به A است — مینویسند: x∉A. به همین ترتیب '⊄' برای زیرمجموعه نبودن است. بعضی جاها از نماد '⊂' برای زیرمجموعه سره بودن و '⊆' برای زیرمجموعه بودن استفاده میشود. ما از ⊂ برای زیرمجموعه بودن استفاده خواهیم کرد. در زیر چند مثال از مجموعه را میتوان دید: | ۱- | {۰, ۱} | ۲- | {۱, ۰} | ۳- | {{۲, ۳}} | ۴- | {{۱}, {۱, ۲}} | | | | | | | | | | | ۵- | {{۲, ۳}} | ۶- | {۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ...} | ۷- | {۱, ۰, ۱} | | | | | | | | | | | | | ۸. | {شیئی|شئ عدد مثبت باشد و شئ مساوی حاصل جمع مقسومعلیههای سره خود باشد} | | | یا | | | {x|x∈ مجموعه اعداد صحیح مثبت & x=(x حاصل جمع مقسومعلیههای سره)} | | | | | | | | | | | | ☚ نشانه | "به قسمی که" خوانده میشود. | | ۹. | {۱} | ۱۰- | {{۱}} | | | | |
مجموعه ۱ و ۲ یکی هستند، زیر ترتیب نمایش اعضای مجموعه فاقد اهمیت است؛ بهعبارتدیگر : برای هر دو شئ {x, y}={y, x}.
مجموعه ۳ تهی است.
در ۴ باید دقت کرد که ۱ و ۲ عضوهای این مجموعه نیستند بلکه فقط مجموعههای {۲ ،۱} و {۱} عضوهای آن هستند و این مجموعه فقط دو عضو دارد و هر دو عضو خود مجموعهاند.
مجموعه ۵ فقط یک عضو دارد.
در ۶ معنی سهنقطه آخر "و مانند آنها" است، یعنی انتظار میرود که ما بقیه عضوها را خواهیم شناخت. اگر ۶ را بهصورت: {...، ۳، ۲، ۱۳، ۲۱، ۵، ۱، ۸} بنویسند آنگاه انتظار نویسنده حداقل از من زیادی است.
و ۷ که همان ۱ است، یعنی تکرار نمایش اعضای مجموعه فاقد اهمیت است، بهعبارتدیگر برای هر شئ داریم: {x, x}={x}.
مجموعه ۸ مجموعه اعداد کامل است؛ مانند ۶ که برابر است با ۱+۲+۳ و همینطور ۲۸، ۸۱۲۸ و مانند آنها. دو مجموعه ۹، ۱۰ هردو تک عضو و با اعضای متمایز هستند، یعنی ۱ و {۱} دو شئ متمایز هستند. یکسان فرض کردن آنها مثل این است که بگوییم هر دارنده یک شئ خودش همان شئ است[جعبه دارای یک سیب خودش سیب است.]
Russell’s Paradox-پارادوکس راسل۱.۷.۱ پارادوکس راسل:آنطور که دیدیم (در مثال ۸ بالا) ممکن است بتوان یک مجموعه را بابیان خاصیت اعضای آن مطابق یکی از قالبهای زیر تعریف کرد: ۱- Δ ={x∈A| Px}
مجموعهای که شامل آن عضوهای A است که دارای خاصیت P هستند. ۲- Δ ={x|x∈A, Px}
مجموعهای که اعضای آن عضو A و دارای خاصیت P هستند. ۳- Δ = {x|Px}
مجموعهای که اعضای آن دارای خاصیت P هستند. در ۱ و ۲ بالا مجموعه Δ بهعنوان زیرمجموعه A تعریف شده و میتوان نوشت: Δ⊂A.
اما تعریف مجموعهای به قالب ۳ قدرتمندتر[فراگیرتر] ازآنچه میتواند باشد است. در پاراگراف بعد خواهیم دید چرا اینگونه قدرتمندی نابودی خود را در خود دارد. برای مثال، مجموعه F را مجموعه همه مجموعههایی بگیرید که خود عضو خود نیستند. بهعبارتدیگر P را x∉xگرفته و مینویسیم: F={x|x∉x}. اگر F وجود داشته باشد آنگاه تهی نخواهد بود. زیرا، برای مثال، مجموعه مادران تکفرزند عضو F است و آشکار است که مجموعه مادران تکفرزند خود یک مادر تکفرزند نیست. در پاراگراف بعد به این میپردازیم که فرض وجود این مجموعه و بنیاد ریاضیات بر اینچنین نظریه مجموعهای موجب میشود تا هر حکم ریاضی اثبات پذیر باشد. یعنی، هر گزاره ریاضی درعینحال که درست، درعینحال نادرست هم باشد. [برای توضیح درباره این نتیجه به بحث ناسازگاری - فصل دهم کتاب را ببینید.] اکنون میپرسیم آیا F عضو خود است؟ اگر F∈F، آنگاه بهموجب P داریم F∉F. اگر F∉F، آنگاه بهموجب P داریم F∈F. آشکارا این یک تناقض است و برخاسته از قالب ۳ (وصف بیحدومرز) در بالا برای تعریف یک مجموعه است. بنابراین (در نظریه طبیعی مجموعهها) چنین نیست که هر وصفی از اشیاء مولد یک مجموعه شود. این به پارادوکس راسل معروف است.به پارادوکس کانتور در همین رابطه که در بحث اعداد کاردینال آمده نیز نگاه کنید. ☚ تعریف یک مجموعه بهصورت {x|x∈A, x∉x} بدون مشکل است و مشمول پارادوکس راسل نیست. تعریف این مجموعه مطابق قالب ۲ است. گوتلوب فرگه واضع اصلی منطق جدید کلاسیک در کتابی که برای نظم و نسق منطقی ریاضیان منتشر نمود قالب ۳ را بهعنوان مولد مجموعه پذیرفته بود. برتراند راسل بعد از خواندن کتاب پی به این پارادوکس برد (ازاینجا این پارادوکس بنام راسل مشهور است) و از طریق نامه به اطلاع فرگه رساند. این باعث شد به استحکام بنای در حال ساخت ریاضیات که در آن زمان بسیار مورد اهتمام ریاضیدانان بود موقتاً خلل وارد شود. درواقع حذف این اصل (قالب ۳) از دستگاه فرگه موجب ناکارایی دستگاه میگردید (آن را بیشازاندازه ضعیف میکرد). چندان طول نکشید که برتراند راسل با ارائه نظریه گونهها /Russell's theory of types این مشکل را از سر راه نظریه مجموعهها برداشت و سپس نیز دستگاه موسوم به دستگاه زیملو-فرانکل/Zermelo–Fraenkel معروف به ZF+C برای مجموعهها [بنیاد قویترین دستگاه ریاضیات جاری] ارائه گردید. ناگفته نماند که از دستگاه فرگه فقط همین یک اصل(قالب ۳) مشکلآفرین بود. همه اصول دیگر فرگه باقوت در دستگاههای بعدی نقش بنیادی خود را دارند.
۸.۱ مجموعه توانی به مجموعهای که اعضای آن همهی زیرمجموعههای یک مجموعه باشند مجموعه توانی آن مجموعه میگویند. فرض کنید؛ {۱ ,۰}=B آنگاه: {{۱ ,۰} ,{۱} ,{۰} ,{ }} که آن را با Ƥ(B) نشانگذاری میکنند، مجموعه توانی B است. اگر تعداد اعضای یک مجموعه n باشد، تعداد اعضای مجموعه توانی آن 2n است و از اینجاست که نام "توان" آمده است. بهعبارتدیگر درازای رشد خطی تعداد اعضای مجموعه، تعداد اعضای مجموعه توانی آن بهطور نمایی/توانی رشد میکند. در زیر چند مثال آمده است: Ƥ(ø)={ø} مجموعه توانی تهی، تهی نیست
Ƥ({۱}) = {ø, {۱}}
Ƥ({۱,۲}) = {ø, {۱}, {۲}, {۱, ۲}}
Ƥ({۱,۲,۳})={ø, {۱}, {۲}, {۳}, {۱, ۲}, {۱, ۳}, {۲, ۳}, {۱, ۲, ۳}}
در مثالهای بالا تعداد اعضای مجموعه توانی یک مجموعه همیشه بیشتر از خود آن مجموعه است. مثال: (روش مکانیکی برای یافتن اعضای مجموعه توانی): مجموعه توانی {T={p, q, r را بیابید: فرض کنید اعضای T گزارههای ساده یک صورت گزارهای باشند. اعداد ۱ تا ۳ را بهدلخواه به آنه گمارده(منتسب میکنیم). فرض کنید این گماردن بهقرار: ۱↔p و ۲↔q و ۳↔r باشد. سپس سه ستون راهنمای جدول-ارزش این صورت گزارهای فرضی را تشکیل میدهیم. از روی آن به شیوه زیر میتوان اعضای مجموعه توانی را حساب کرد. | pqr | ۱ ۲ ۳ | | 111 | {p, q, r} | | 110 | {p, q } | | 101 | {p, r} | | 100 | {p } | | 011 | { q, r} | | 010 | { q } | | 001 | { r} | | 000 | { } |
۹.۱ مشاهیر مجموعهها از مشاهیر یکی مجموعه تهی است که معرفی شد و دیگری مجموعه اعداد طبیعی است که معرف حضور است و آدمیزاد میخواهد هر چیزی را فقط با آن حساب کند. یکی از سیارات نیز همین سیاره شمارش است(اخترک چهارم/شازده کوچولو). مجموعه اعداد طبیعی یعنی {.... ,۳ ,۲, ۱} نیز مثل ∅ نشان مخصوص خود، یعنی  را دارد ➥. [*]--بعضی متون صفر را جزو اعداد طبیعی آورده و بعضی نمیآورند. اعضای این مجموعه ازجمله مهمترینهای دنیا و همینطور پر سابقهترین هستند. مجموعه  [از مجموعههای با سر بی ته است.] مجموعه بعدی همه اعضای  را دارد [ولی بیسر و بی ته است.] این مجموعه که اعداد صحیح نام و را دارد [ولی بیسر و بی ته است.] این مجموعه که اعداد صحیح نام و 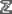 را نشان دارد بهقرار {. . . ،۲ ، ۱، ۰، ۱-، ۲-، .. . .} است. را نشان دارد بهقرار {. . . ،۲ ، ۱، ۰، ۱-، ۲-، .. . .} است. مجموعه بعدی اعداد گویا/rational نام و 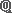 را نشان دارد. این مجموعه همه عضوهای را نشان دارد. این مجموعه همه عضوهای 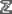 را دارد بعلاوه اعداد با حداقل یک رقم اعشاری غیر صفر. تعداد ارقام اعشاری میتوانند (نامتناهی) باشند و البته باید از جای معینی به بعد رشته متناهی از آنها تکرار شود. اعداد گویا همان اعداد کسری (دارای صورت و مخرج) هستند(قدیمتر تبدیل این دو را به هم رفع و تجنیس میگفتند.) را دارد بعلاوه اعداد با حداقل یک رقم اعشاری غیر صفر. تعداد ارقام اعشاری میتوانند (نامتناهی) باشند و البته باید از جای معینی به بعد رشته متناهی از آنها تکرار شود. اعداد گویا همان اعداد کسری (دارای صورت و مخرج) هستند(قدیمتر تبدیل این دو را به هم رفع و تجنیس میگفتند.) در عالم اعداد گویا، عدد ۲/۱، یعنی همان تقسیم دو بر یک، جذر ندارد(ثابت کردن آن آسان است). 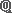 برای بقای گویایی باید چنین حفرهای را ندیده بگیرد. و البته این حفرهها یکی دوتا هم نیستند. ازجمله عدد معروف پی، یعنی اندازه نسبت محیط دایره به قطر خود که برای هر دایره ثابت است. داستان فیثاغورثیان و اندازه وتر مثلث قائمالزاویه متساویالساقین با ساقهای بهاندازه ۱، خود بهاندازه اعداد گویا مشهور است. نگاه نزدیکتر را میتوان معمولاً در فصلهای یکم و دوم کتابهای آنالیز ریاضی جست. برای بقای گویایی باید چنین حفرهای را ندیده بگیرد. و البته این حفرهها یکی دوتا هم نیستند. ازجمله عدد معروف پی، یعنی اندازه نسبت محیط دایره به قطر خود که برای هر دایره ثابت است. داستان فیثاغورثیان و اندازه وتر مثلث قائمالزاویه متساویالساقین با ساقهای بهاندازه ۱، خود بهاندازه اعداد گویا مشهور است. نگاه نزدیکتر را میتوان معمولاً در فصلهای یکم و دوم کتابهای آنالیز ریاضی جست. مجموعهای که علاوه بر اعداد گویا حفرهها را که به آنها اعداد گنگ/irrational میگوییم داشته باشد، معروف به مجموعه اعداد حقیقی/Real و به  نشانهدار است. نشانهدار است. در انتهای مراسم معرفی: +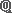 مجموعه اعداد گویای مثبت،* مجموعه اعداد گویای مثبت،*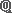 مجموعه اعداد گویای غیر صفر هستند و مانند آنها نیز برای مجموعه اعداد گویای غیر صفر هستند و مانند آنها نیز برای 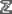 و و  . .
۱۰.۱ اعمال روی مجموعهها مجموعه C را اشتراک دو مجموعه A و B گویند اگر و فقط اگر عضوی در C نباشد که در A و B نباشد, و مینویسند C=A ∩ B. دو مجموعه ازهمجدا هستند اگر اشتراک آنها تهی باشد. مجموعه U را اجتماع دو مجموعه A و B میگویند اگر و فقط اگر عضوی در U نباشد که در A یا در B (یا در هردو) نباشد, و مینویسند U=A∪B. ☚ اشتراک تهی با خود تهی است و اجتماع تهی با هر مجموعه خود آن مجموعه است. تفاضل مجموعهها: مجموعه D را تفاضل مجموعه B از A گویند و نوشتهD=A - B ، [همچنینD=A/B ] اگر و فقط اگر عضوهای D همه عضوهایی باشد که در A هست و در B نیست. اگر D=A/B آنگاه به D متمم مجموعه A نسبت به B میگویند. اگر A و B از هم جدا باشند آنگاه: A=A-B و B=B-A . اگر درزمینهی بحث چنین پیشفرض باشد که همه مجموعهها زیرمجموعه یک مجموعه تثبیتشده مانند M هستند(برای مثال بحث درباره اعداد)، آنگاه به M-A متمم A گفته و آن را با 'A نشان میدهند.
۱۱.۱ دوتایی مرتب گاه نیازمندیم برای اعضای مجموعهای مانند A={a, b} به نحوی ترتیب قائل شویم و برای مثال a را عضو اول و b را عضو دوم بنامیم. در این مواقع این ترتیب را با یک الحاقی، بهصورت <a, b>، منظور میکنیم و میگوییم بنا به این الحاقی، یعنی <a, b>، و فارغ از ترتیب حضور اعضا در a ،A عضو نخست و b عضو بعدی A است. به <a, b> یک دوتایی مرتب گفته میشود. بنابراین وقتی a و b یکی نیستند <a, b> و <b, a> دو ترتیب متمایز را در {a, b} برای a و b مشخص میکنند. به همین نحو میتوان از سهتاییهای مرتب مانند <b, a, c> و بهطورکلی از nتاییهای مرتب مانند:
<a۱, a۲, ...,an> صحبت کرد. بهجا است پرسیده شود سرشت ریاضی این "الحاقی ترتیبی" چیست؟ جواب این است که یک دوتایی و بهطورکلی nتایی مرتب یک مجموعه است. در مورد دوتایی مرتب داریم؛ <a, b>={{a}, {a, b}} بنابراین: دوتایی مرتب <a, b> فارغ از مجموعه A (در بالا) خود بیان شدنی است. ◀ دوتایی مرتب <x, y> بهصورت (x, y) نیز نوشته میشود. ◀ برای هر دوتایی مرتب <x, y> داریم: <x, y>= <a, b> ⇔ x=a & y=b.
۱۲.۱ ضرب دکارتی مجموعهها: اگر X و Y مجموعه باشند آنگاه ضرب دکارتی X در Y مجموعه همه دوتاییهای مرتب است به قسمی که عنصر اول آنها در X و عنصر دوم آنها در Y باشد. بهعبارتدیگر: ضرب دکارتی دو مجموعه X و Y: X×Y={(x,y)| x∈X & y∈Y}. مثال: فرض کنید A و B به ترتیب {a ،b ،c} و {۱ ،۰} باشند، آنگاه A×B={(a, ۰), ( b, ۰), (c, ۰), (a, ۱), (b, ۱), (c, ۱)};
B×A={(۰, a), (0, ۰), (۰, c), (۱, a), (۱, b), (۱, c)}. | | | | B×A | | | | | | | A×B | | | | | / | | \ | | | / | | | | | \ | | | ۰ | | | | ۱ | | a | | b | | c | | / | | | \ | | / | | | \ | /\ | | /\ | | /\ | | a | b | b | | a | b | b | ۰ ۱ | | ۰ ۱ | | ۰ ۱ | | | | | | | | | | | | | |
◀ ضرب دکارتی دو مجموعه خاصیت جابجایی ندارد. مثال: خط، صفحه و فضای اقلیدسی نمایش هندسی(اقلیدسی) مجموعههای زیر هستند( به ترتیب از چپ به راست):  1= 1= ; ;  2 = 2 =  × × ; ;  3= 3= × × × × . .
☚ اگر مجموعه A دارای n عضو و مجموعه B دارای m عضو باشد، آنگاه A×B دارای n×m عضو خواهد بود.
Relation-رابطه۱۳.۱ رابطه: به مجموعهای از nگانههای مرتب یک رابطه nتایی میگویند. بهعبارتدیگر، هر مجموعه nگانه مرتب یک رابطه را تعریف میکند. برای مثال، مجموعه سهگانههای مرتب: (x, y, z)∈ × × × × به قسمی که xبین y و z باشد، به قسمی که xبین y و z باشد، یک رابطه را در  تعریف میکند. ازآنجاکه یک رابطه یک مجموعه است همه اعمال مجموعهها برای آن نیز جاری خواهد بود. اگر نام رابطه اخیر را R بنامیم، آنگاه: تعریف میکند. ازآنجاکه یک رابطه یک مجموعه است همه اعمال مجموعهها برای آن نیز جاری خواهد بود. اگر نام رابطه اخیر را R بنامیم، آنگاه: R={(x, y, z)|x, y, z ∈ & y<x<z} & y<x<z} و مینوان نوشت: (۱۳, ۱۱, ۲۱)∈R ; (۱۳, ۱۱, ۱۱)∉R مثال: دو مجموعه A و B بالا، ۱۲.۱، را در نظر بگیرید. هریک از دو مجموعه زیر: R۱ = {(۰, a), (۰, b), (۰, c)}⊂A ×B ; R۲ = {(۰, ۱), (۱,۰)}⊂A ×A=A۲ دو رابطه متمایز را تعریف میکنند. مینویسیم: (۱, b)∈R۱ و میگوییم: ۱ در رابطه R۱ با b است. همچنین مینویسیم: (۱, b)∉R۲ و میگوییم: ۱ در رابطه R۲با b نیست. | ☚ | علاوه به نوشتن (x, y)∈R برای نشان دادن در رابطه R بودن x با y، آن را بهصورت xRy نیز نشان میدهند. بنابراین میتوان نوشت: ۱R۱ b و ۱R۱ a. |
۱.۱۳.۱ رابطه تهی: مجموعه تهی زیرمجموعه هر مجموعهای است، بنابراین مجموعه تهی یک رابطه است و میتوان از آن بدون ابهام از رابطه تهی نام برد زیرا فقط یک رابطه تهی وجود دارد.
۲.۱۳.۱ رابطه یکتایی: هر زیرمجموعه یک مجموعه، یک رابطه یکتایی را در آن مجموعه تعریف میکند. برای مثال، زیرمجموعه زنان دارای فرزند در مجموعه انسانها یک رابطه یکتایی، مادری، را تعریف میکند. به یک رابطه یکتایی در یک مجموعه یک ویژگی (خاصیت، محمول تک موضعی) در آن مجموعه میگویند. مانند ویژگی مادری در مجموعه انسانها، مادری در مجموعه زنان، عدد فرد بودن در مجموعه اعداد طبیعی، 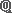 بهعنوان زیرمجموعه بهعنوان زیرمجموعه  (گویایی در اعداد حقیقی) و مانند آنها. (گویایی در اعداد حقیقی) و مانند آنها. فرض کنید P ویژگی(رابطه یکتایی) گویایی در اعداد حقیقی باشد، در این صورت برای نشان دادن این ویژگی برای شیئی مانند a نوشته Pa [یا P(a)] و میخوانیم a عدد گویا است.
۳.۱۳.۱ رابطه دوتایی: برای n = ۲ رابطه را یک رابطه دوتایی میگویند. اگر A و B مجموعه باشند،A×B و هر زیرمجموعه آن یک رابطه دوتایی از A در B را تعریف میکند. وقتی دو مجموعه (بهطورکلی عوامل ضرب) یکی، به فرض A، باشند، معمولاً بهجای "رابطه از A در A" میگویند "رابطه در A". برای مثال اگر A مجموعه انسانها باشد آنگاه: R = {(x, y)|x, y∈A & است y برادر x} یک رابطه دوتایی(برادری) را در A تعریف میکند. فرض کنید a (پرویز) برادر b (پروین) باشد؛ در این صورت مینویسیم: (a, b)∈R یا aR b نیز (b, a)∉R یا bR a.
۱.۳.۱۳.۱ رابطه تساوی/همانندی: برای مجموعه دلخواه A، به رابطه{(x, x)|x∈A} یک رابطه تساوی (یا همانندی/=) میگوییم.
۴.۱۳.۱ دامنه رابطه فرض کنید R یک رابطه در A باشد. دامنه رابطه Rمجموعه xهای متعلق به A است، به قسمی که برای حداقل یک y∈A داشته باشیم: (x, y)∈R. Domain(R)={x|x∈A & a∈A, xRa} برای مثال اگر R را رابطه برادری و A را مجموعه انسانها بگیریم آنگاه دامنه R مجموعه همه انسانهایی است که برادر حداقل یک نفر هستند. [هیچ مادری عضو دامنه این رابطه نیست.]
۵.۱۳.۱ قلمرو رابطه: فرض کنید R یک رابطه در A باشد. قلمرو رابطه R مجموعه yهای متعلق به A است، به قسمی که برای حداقل یک x∈A داشته باشیم: (x, y)∈R. Range(R)={y|y∈A & a∈A, aRx} برای مثال اگر R را رابطه برادری و A را مجموعه انسانها بگیریم آنگاه قلمرو R مجموعه همه انسانهایی است که دارای حداقل یک برادر هستند. [یک مادر ممکن است عضو قلمرو این رابطه باشد.]
۶.۱۳.۱ میدان رابطه: فرض کنید R یک رابطه در A باشد. اجتماع دامنه و قلمرو R ر میدان رابطه R مینامند. Field(R)=Domain(R) ∪ Range(R) برای مثال اگر R رابطه برادری و A را مجموعه انسانها بگیریم آنگاه میدان R مجموعه همه انسانهایی است که خود برادر کسی هستند یا دارای برادر هستند. برای مثال اگر پرویز برادر پروین باشد آنگاه هر دو عضو میدان R هستند.
۷.۱۳.۱ گونههای ساده روابط ۱.۷.۱۳.۱ رابطه انعکاسی: رابطه دوتایی R را رابطه انعکاسی گویند اگر: برای هر عضو میدان R مانند x داشته باشیم: xR x. رابطه ≤ (بزرگتر یا مساوی) و نیز ≥ (کوچکتر یا مساوی) در  انعکاسیاند ولی > (کوچکتر) و < (بزرگتر) جنین نیستند. انعکاسیاند ولی > (کوچکتر) و < (بزرگتر) جنین نیستند.
۲.۷.۱۳.۱ رابطه متقارن: رابطه دوتایی R را رابطه متقارن گویند اگر : برای هر دو عضو میدان R مانند x, y، اگر xR y آنگاه yR x. رابطه برادری در انسانها یک رابطه متقارن نیست؛ زیرا از اینکه a برادر b است لزوماً به دست نمیآید b برادر a است. همچنین رابطه ≥ در  متقارن نیست. رابطه تساوی در هر میدان متقارن است. متقارن نیست. رابطه تساوی در هر میدان متقارن است.
۳.۷.۱۳.۱ رابطه پادمتقارن: رابطه دوتایی R را رابطه پادمتقارن گویند اگر : برای هر دو عضو میدان R مانند x, y، اگر xR y و yR x آنگاه y= x. بهعبارتدیگر برای هر y≠x در میدان R چنین نیست که xR y و yR x. رابطه < در  پادمتقارن است. رابطههای: پادمتقارن است. رابطههای: {(۱,۲) ,(۲, ۳),(۴, ۱)} و {(۱,۱), (۳, ۳)} در{۱, ۲, ۳, ۴} پادمتقارن هستند.
۴.۷.۱۳.۱ رابطه ترایایی: رابطه دوتایی R را رابطه ترایایی گویند اگر برای هر سه عضو میدان R مانند x, y, z: xR y & yR z ⇒ xR z. رابطه ≥ در  ترایاییاند. رابطه برادری در انسانها ترایایی نیست. ترایاییاند. رابطه برادری در انسانها ترایایی نیست.
۵.۷.۱۳.۱ رابطه ترتیبی جزئی به رابطهای که ۱- انعکاسی؛ ۲- پادمتقارن؛ ۳- ترایایی باشد یک رابطه ترتیبی جزئی میگویند. رابطههای ≤ و ≥ در 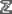 ترتیبی جزئی هستند. ترتیبی جزئی هستند.
۷.۷.۱۳.۱ مقایسه پذیری: ففرض کنید که (A,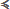 ) یک مجموعه مرتب جزئی و a و b دو عضو آن باشند. میگوییم a و b مقایسه پذیر اند اگر a ) یک مجموعه مرتب جزئی و a و b دو عضو آن باشند. میگوییم a و b مقایسه پذیر اند اگر a 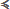 b یا b b یا b 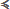 a. a.
۸.۷.۱۳.۱ مجموعه مرتب کامل فرض کنید که (A(A, 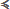 ) یک مجموعه مرتب جزئی، اگر هر دو عضو A مقایسه پذیر باشند آنگاه A را مرتب کامل و نیز ) یک مجموعه مرتب جزئی، اگر هر دو عضو A مقایسه پذیر باشند آنگاه A را مرتب کامل و نیز 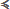 را یک رابطه ترتیبی کامل یا رابطه خطی مینامند. را یک رابطه ترتیبی کامل یا رابطه خطی مینامند.
۹.۷.۱۳.۱ مجموعه خوشترتیب یک مجموعه مرتب کامل را مجموعه خوش-ترتیب گویند اگر و فقط اگر هر زیرمجموعه آن دارای کوچکترین عضو باشد. برای مثال، مجموعه 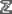 خوشترتیب نیست. خوشترتیب نیست.
۱۱۰.۷.۱۳.۱ اصل خوشترتیبی اصل خوشترتیبی میگوید: مجموعه اعداد طبیعی خوشترتیب است. یعنی، هر زیرمجموعه اعداد طبیعی دارای کوچکترین عضو است.
۸.۱۳.۱ رابطه همارزی: رابطه دوتایی R را رابطه همارزی گویند اگر R:
۱-نعکاسی، -۲متقارن و -۳ترایایی باشد. رابطه تساوی/همانندی(=) یک رابطه همارزی است. ولی رابطههای برادری در انسانها، ≥ در 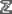 و همشهری(آ و ب همشهریاند اگر تابعیت حداقل یک کشور را داشته باشند) همارزی نیستند. و همشهری(آ و ب همشهریاند اگر تابعیت حداقل یک کشور را داشته باشند) همارزی نیستند. به شیوهای که در پی میآید خواهیم دید، با بهرهگیری از رابطه همارزی بهجای پرداختن به یک مجموعه نامتناهی(تعریف دقیق نامتناهی در ادامه همین یادداشت آمده است)، وقتی موردتوجه رابطه همارزی خاصی در آن است، میتوان با یک مجموعه متناهی سروکار داشت و پیچیدگیهای بیهوده در این زمینه را فرو کاهید. هر رابطه همارزی، به فرض ≡، میدان خود را به زیرمجموعههای دوبهدو از هم جدا تقسیم (افراز) میکند، به قسمی که: ۱- هر دو عضو متعلق به هر یک از این زیرمجموعهها باهم در رابطه ≡ هستند؛ ۲- هیچ دو عضو متعلق به دو زیرمجموعه متمایز در رابطه ≡ نیستند؛ ۳- اجتماع زیرمجموعههای افرازی مساوی میدان رابطه ≡ است. این زیرمجموعهها را کلاسهای همارزی ≡ میگویند. ازآنچه گفته شد برمیآید، اگر C۱ و C۲ دو کلاس همارزی ≡ باشند و دارای حداقل یک عضو مشترک باشند لزوماً داریم C۱=C۲. بهعبارتدیگر، فرض کنید ≡ یک رابطه همارزی و D≠Φ میدان آن باشد. در این صورت به: CxD = {x ∈D|x ≡a, a∈D} که یک زیرمجموعه D است کلاس همارزی ≡ در D به نمایندگی x میگوییم. میتوان نشان داد برای هر x, y∈D داریم: ۱: x≠ y ⇔ CxD ∩CyD=Φ ۲: x=y ⇔ CxD= CyD و اگر تعداد کلاسهای همارزی را n∈ بگیریم: بگیریم: ۳: Cx۱D∪Cx۲D ∪. . .∪CxnD=D
۱.۸.۱۳.۱ رابطه همنهشتی در  ∪{۰}: ∪{۰}: مثال: فرض کنید رابطه R۵ را در مجموعه  ∪{۰} اینگونه تعریف کنیم: xR۵y اگر باقیماندههای حاصل از تقسیم صحیح x و y به ۵ مساوی باشند (بهعبارتدیگر، تفاضل آنها به ۵ بخشپذیر باشد). بنابراین داریم: ∪{۰} اینگونه تعریف کنیم: xR۵y اگر باقیماندههای حاصل از تقسیم صحیح x و y به ۵ مساوی باشند (بهعبارتدیگر، تفاضل آنها به ۵ بخشپذیر باشد). بنابراین داریم: ۰،R۵۵ ،۵R۵۱۰ ،۱۰R۵۵ ،۵R۵۵ ،۰R۵۱۵ ،۱R۵۶ ،۶R۵۱۱ ۱R۵۱۱ و مانند آنها. بهآسانی میتوان نشان داد R۵ یک رابطه همارزی است و  ∪{۰} را به پنج کلاس همارزی ۰ ,۱, ۲, ۳, ۴ بهقرار زیر: ∪{۰} را به پنج کلاس همارزی ۰ ,۱, ۲, ۳, ۴ بهقرار زیر: ۰= {x |به ۵ بخشپذیر باشد. x-۰}= {۰, ۵, ۱۰, ۱۵, ۲۰, . . .} ۱={x |به ۵ بخشپذیر باشد. x-۱}= {۱, ۶, ۱۱, ۱۶, ۲۱, . . .} . . . . . . . . . . . . . . ۴={x |به ۵ بخشپذیر باشد. x-۴}= {۴, ۹, ۱۴, ۱۹, ۲۴, . . .} افراز میکند. میتوان دید که:  ∪{۰}= ۰∪۱∪۲∪۳∪۴ ∪{۰}= ۰∪۱∪۲∪۳∪۴
به R۵ رابطه همنهشتی(به سنج/از سنجیدن ۵) گفته و مینویسند: ۱[۵ به سنج] =۶[۵ به سنج] و نیز مانند آن برای بقیه. رابطه همنهشتی را میتوان برای n∈ تعمیم داد. میگوییم k, l∈ تعمیم داد. میگوییم k, l∈ ∪{0} به سنج n همنهشت هستند و مینویسیم: ∪{0} به سنج n همنهشت هستند و مینویسیم: k [n به سنج] = l اگر و فقط اگر k-l ،n را بشمارد.
۹.۱۳.۱ مثالهایی از رابطه: فرض کنید E مجموعه انسانها و Rz و Rm به ترتیب ویژگیهای(رابطههای یکتایی) زن بودن و مرد بودن در E باشند، آنگاه: R۱={( x, y)|Rz(x) & Rm(y)} : دوتاییهایی که اولی زن و بعدی مرد R۲={(x, y)|xR1y & (است x همسر y)} :رابطه زنوشوهری R۳={(x, y)| x, y∈(Rz∪Rm) & (است x فرزند y)} :رابطه فرزندی R۴={(x, y, z)|xR۲y & xR۳z & yR۳z & z∈Rz} :زن و شوهرهای با حداقل ۱ فرزند دختر R۵={(x, y, w, z)|(x, y, w)∈R۴ & (x, y, z)∈R۴ & w≠z} :زن و شوهرهای با حداقل ۲ فرزند دختر
۱۴.۱ تابع: | ☚ | نام دیگر تابع نگاشت [نگاشتن - نگاریدن - تصویر کردن - map - mapping) است. وقتی زمینه بحث بیشتر مفاهیم گسسته باشد از این نام استفاده میشود. |
فرض کنید S و T دو مجموعه باشند. بسیار پیش میآید که میخواهیم به S از منظرهای ممکن T نگاه کنیم. بهعبارتدیگر میخواهیم S را مصور در T ببینیم. مثال ساده آن یافتن معادل واژه فارسی "باران" در واژهنامه فارسی-انگلیسی، و بهعبارتدیگر دیدن تصویر واژه "باران" بهعنوان عضوی از مجموعه واژگان فارسی در مجموعه واژگان انگلیسی است. به این مفهوم بهطور عام یک تابع از S به(در) T گفته میشود. یک تابع وقتی از S در T معنی مییابد (تعریف میشود) که برای هر عضو S یک و فقط یک عضو از T مصور باشد (عضوی در S بدون تصویر باقی نماند و فقط هم یک تصویر در T داشته باشد). با توجه به تعداد عضوهای S و T میتوان چندین تابع از S به T تعریف کرد (از چندین نظرگاه در S به T نگاه کرد.) بنابراین، با تعریف هر تابع از S به T یک تصویر S را در T خواهیم داشت. معمولاً توابع را با حروفی کوچک لاتین مانند g ،f و مانند آنها نامگذاری میکنند. وقتی تابعی از S در T بنام f تعریف شود، این تعریف را بهصورت شماتیکSchema: f : S→T (I) نشان میدهند. S را دامنه تابع یا مجموعه عزیمت تابع و آن زیرمجموعه از T را که اعضای آن تصویر عضوی از S هستند را برد تابع f میگویند. خود مجموعه T مجموعه مقصد تابع f نام دارد. دامنه یک تابع مانند fرا با Domainf و برد آن را با Rangef نشان میدهند. مهم اول در تعریف یک تابع این نیست که چگونه تصویر یک عضو دامنه را باید پیدا کرد، مهم اول شناسایی مجموعههای عزیمت و مقصد است و نشان دادن اینکه که «هر عنصر دلخواه مجموعه عزیمت، به فرض S، تحت تابع تعریفشده، به فرض f، دارای تصویر در مجموعه مقصد، به فرض T، است». عبارت داخل گیومه را معمولاً اینگونه مینویسند: برای هر x∈S اگر،x آنگاه f(x)∈T مسئله بعد میتواند این باشد که برای یک x خاص در S چگونه میتوان (f(x را یافت. روشهای مختلف برای این کار هست که بستگی به مجموعههای مقصد و عزیمت و مهمتر قصد تعریف تابع دارد. ازجمله نوشتن یک عبارت جبری است که به آن ضابطه تابع نیز میگویند. برای مثال فرض کنید S و T هردو  باشند، آنگاه: باشند، آنگاه: e : → →  ; e(x)=۲x-۱. ; e(x)=۲x-۱. یعنی، بهواسطه e میتوان گفت برای هر عدد طبیعی یک عدد فرد نظیر وجود دارد (توجه: ما صفر را عدد طبیعی فرض نکردهایم.) طریقههای دیگری ازجمله رسم نمودارهای مختلف و همینطور جداول مرسوم است. به تابع f در (I) یک تابع یکبهیک/Injective/one to one/Embedded (بهصورت نمادین ۱:۱) میگویند اگر و فقط اگر عضوی در Tنباشد که تصویر دو عضو متمایز Sباشد. بهعبارتدیگر، اگر a و b دو عضو متمایز S باشند، آنگاه (f(a و (f(b، یعنی تصاویر آنها، نیز متمایز باشند. [برای مثال، تابع e در بالا ۱:۱(یکبهیک) است.] اگر برد تابع همه T باشد (عضوی در T نیست که تصویر عضوی از S نیست) آنگاه به f یک تابع پوشا /Onto گفته میشود. [تابع e در بالا پوشا نیست.] اما تابع : d: ↦ E ; d(x)=2x-1. ↦ E ; d(x)=2x-1. که در آن E مجموعه اعداد فرد است پوشا است. تابعی که هم ۱:۱ و هم پوشا باشد را تابع دو سویی میگویند. اگر f دو سویی باشد آنگاه بهخودیخود یک تابع دیگر از T در S تعریف میشود. برای نشانهگذاری این تابع از حرف جدیدی استفاده نمیشود و آن را با f -۱ نشانهگذاری میکنند و به آن تابع وارون f گفته میشود. اگر f دو سویی باشد میگوییم بین S و T یک تناظر یکبهیک (بهواسطه f) برقرار است. فرض کنید A و B دو مجموعه، گوییم بین این دو یک رابطه تناظر وجود دارد اگر حداقل یک تابع دو سویه از یکی از آنها در دیگری وجود داشته باشد. تناظر بین دو مجموعه را با نماد '⇌' نشان داده و مراد از نوشتن A⇌B وجود حداقل یک تابع دو سویی بین A و B است. توابع را همانطور که در بالا گفته شد ازجمله میتوان با استفاده از یک جدول دو سطری (یا دو ستونی) نمایش داد. در جداول زیر به ترتیب سه تابع t و v ،g تعریف شدهاند. g تعریف تابع
| g : S ↦ B; S={۰, ۱, ۲, ۳, ۴, ۵}; B={۰, ۱} | | e ∈S | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | | g(e)∈B | ۰ | ۱ | ۰ | ۱ | ۰ | ۱ | تابع g پوشا است ولی یکبهیک نیست |
| v تعریف تابع | v : B ↦ Σ; B={۰, ۱}; Σ={ ۰, ۲, ۴, . . .} | | e∈B | ۰ | ۱ | | v(e)∈Σ | ۰ | ۱ | تابع v پوشا نیست ولی یکبهیک است |
t تعریف تابع
| t: B ↦ Γ; B= {۰,۱}; Γ={{۰, ۲, ۴, ... }, {۱, ۳, ۵, ۷, ۹, . . .}} | | e ∈B | ۰ | ۱ | | t(e)∈Γ | {۱, ۲, ۴, . . .} | {۱, ۳, ۵, ۷, ۹, . . .} | | تابع t پوشا و یکبهیک است، لذا بین B و Γ تناظر یکبهیک بهواسطه t برقرار است و میتوان نوشت B⇌Γ. |
◄ اگر تابع f از S در T پوشا باشد، آنگاه هر زیرمجموعه ناتهی T تصویر یک زیرمجموعه S است. ◄ ازجمله توابع معروف تابع همانی است که برای او قصد هر عزمی خودش است یا بهعبارتدیگر مجموعه عزیمت و مقصد آنیکی و تصویر هر عضو، خود آن عضو است (دنیا را از چشم خودش میبیند و نیز در آن فقط خودش را). این تابع را با idS نشان میدهند (S هم مجموعه عزیمت و هم مقصد است)، بنابراین idS(x)=x. آشکار است که این تابع یکبهیک و پوشا است و (حتی!) وارون آن نیز خودش است. ◄ تابع معروف دیگر تابع ثابت نام دارد که تصویر هر عضو مجموعه عزیمت فقط یک عضو از مجموعه مقصد است(مرغ یک پا دارد). اگر مجموعه عزیمت بیش از یک عضو داشته باشد آنگاه این تابع وارون ندارد. اگر این تابع پوشا باشد آنگاه مجموعه مقصد تک عضوی است. ۱.۱۴.۱ تابع و رابطه: مفاهیم زوج مرتب، حاصلضرب دکارتی و رابطه که تاکنون معرفی شدند همه طبق تعریف گونهای از مجموعه بودند. بهعبارتدیگر اصلیترین جنس آنها مجموعه است. تابع نیز چنین است. درواقع تابعی مانند f از مجموعه A در مجموعه B یک رابطه از A در B است به قسمی که: ۱- هر عضو A در رابطه fبا B باشد؛ ۲- هیچ عضو A در رابطه f با دو عضو متمایز B نباشد. (b۱=b۲ ⇐ afb۱ & afb۲)
۲.۱۴.۱ توابع سازگار: دو تابع f و g را توابع سازگار گوییم اگر برای هر x متعلق به Domainf∩Domaing داشته باشیم f(x)=g(x).
۱۵.۱ ترکیب توابع فرض کنید f و g توابع زیر باشند: f : S ↦ T; g : T ↦ V; ترکیب تابع g با f تابعی از S به V است، که آن را بهصورت g f نشان داده و مطابق زیر تعریف میکنیم: f نشان داده و مطابق زیر تعریف میکنیم: g  f : S ↦ T; f : S ↦ T; g  f(x) =f (g(x) )بهگونهای که: در جدول فوق، I یعنی g f نگاه به B است از منظر V با واسطهگری S. f نگاه به B است از منظر V با واسطهگری S.
۱۶.۱ مجموعههای متناهی و نامتناهی: بهطور شهودی میتوان دید  یک مجموعه نامتناهی است و همینطور مجموعه اعداد صحیح، یعنی: یک مجموعه نامتناهی است و همینطور مجموعه اعداد صحیح، یعنی: 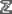 ={. . ., -۳, -۲, -۱, ۰, ۱, ۲, ۳ ,. . .} ={. . ., -۳, -۲, -۱, ۰, ۱, ۲, ۳ ,. . .}
نیز نامتناهی است. هدف این بند تعریف دقیق نامتناهی بودن یک مجموعه است. ابتدا به مثال زیر توجه نمایید. مثال: مجموعه اعداد زوج، یعنی {۰, ۲, ۴, ۶, . . .}⊂ را E مینامیم. روشن است که E⊂ را E مینامیم. روشن است که E⊂ . نگاشت g از . نگاشت g از  در E را مطابق جدول زیر تعریف میکنیم. در E را مطابق جدول زیر تعریف میکنیم. g :  ↦ E; ↦ E; | | تعریف تابع g | | . | . | . | ۵ | ۴ | ۳ | ۲ | ۱ | ۰ | x∈ | | . | . | . | ۱۰ | ۸ | ۶ | ۴ | ۲ | ۰ | g(x)∈ | | g(x)=۲x | | بهموجب تابع g، یک تناظر ۱:۱ بین اعداد طبیعی و زیرمجموعه سرهای از آن، یعنی اعداد زوج، وجود دارد. |
ازآنجاکه، برای هر n∈ نظیر آن، ۲n، در E و نیز برای هر عضو e∈E نظیر آن، ۲/e، در نظیر آن، ۲n، در E و نیز برای هر عضو e∈E نظیر آن، ۲/e، در  وجود دارد، نگاشت g دو سویی است، یعنی بین وجود دارد، نگاشت g دو سویی است، یعنی بین  و یک زیرمجموعه سره آن، در این مثال اعداد زوج، یک تناظر ۱:۱ وجود دارد و میتوان نوشت: و یک زیرمجموعه سره آن، در این مثال اعداد زوج، یک تناظر ۱:۱ وجود دارد و میتوان نوشت:  ⇌E. ⇌E. بهعبارتدیگر، اعضای  با اعضای زیرمجموعه سرهای از آن جفت شدنی است و این در حالی است که عضوهایی در با اعضای زیرمجموعه سرهای از آن جفت شدنی است و این در حالی است که عضوهایی در  هست که در E نیست. [به گونه دیگر، هست که در E نیست. [به گونه دیگر،  بهعنوان یک کل با جزئی از خود هماندازه است. این ویژگی بهعنوان یک کل با جزئی از خود هماندازه است. این ویژگی  را نامتناهی بودن را نامتناهی بودن  نامیده.] [نیز: کتابی را تصور کنید که تعداد صفحههایش با تعداد صفحههای فصل آخر آن برابر است. اگر چنین کتابی باشد، این کتاب چند صفحه باید داشته باشد؟] نامیده.] [نیز: کتابی را تصور کنید که تعداد صفحههایش با تعداد صفحههای فصل آخر آن برابر است. اگر چنین کتابی باشد، این کتاب چند صفحه باید داشته باشد؟] مجموعه نامتناهی: بک مجموعه را نامتناهی گوییم اگر بین آن و زیرمجموعه سرهای از آن یک تناظر ۱:۱ وجود داشته باشد. به مجموعهای که نامتناهی نیست مجموعه متناهی میگویند. برای مثال هر زیرمجموعه  که دارای بزرگترین عضو باشد، یا بدانیم اعضای آن از یک عدد طبیعی کوچکترند، یک مجموعه متناهی است. که دارای بزرگترین عضو باشد، یا بدانیم اعضای آن از یک عدد طبیعی کوچکترند، یک مجموعه متناهی است. ۱.۱۶.۱☚ متمم زیرمجموعههای متناهی اعداد طبیعی نامتناهیاند ولی عکس آن همیشه درست نیست. ۲.۱۶.۱☚ با استفاده از اصل خوش-ترتیبی میتوان نشان داد بین هر زیرمجموعه نامتناهی  و خود و خود  تناظر ۱:۱ برقرار است. تناظر ۱:۱ برقرار است.
۱۷.۱ شمارایی و کاردینال: میتوان به مجموعههای متناهی عددی که بهاندازه تعداد اعضای آن مجموعه باشد نسبت داد و آنان را مقایسه پذیر نمود. آیا مجموعهای نامتناهی نیز مقایسه پذیراند؟ هدف این بند نشان دادن این است که چگونه ریاضیدانان مفهوم مقایسه پذیری را گسترانده تا بهطور عام برای مجموعهها، متناهی و نامتناهی، کار زدنی باشد. داستان از شمارایی[شمارشپذیری] مجموعهها آغاز میشود. بهطور شهودی، مجموعهای شمارا است که بتوان اعضای آن را توسط اعداد طبیعی فهرست کرد (برشمرد/شماره بندی کرد). البته همانطور که خواهیم دید مجموعههایی نیز هستند که شمارا نیستند و اعضای آنها را نمیتوان برشمرد. شمارایی رهنمون ما به مفهوم بینهایت(ها) / اعداد نامتناهی و حساب آنها است. اینک تعریف دقیق شمارایی یک مجموعه: ۰.۱۷.۱ مجموعه شمارا: مجموعه S را یک مجموعه شمارا گویند اگر و فقط اگر S تهی باشد؛ ی از  یا زیرمجموعهای از یا زیرمجموعهای از  در S یک تابع پوشا، به فرض f، وجود داشته باشد. در این صورت میگوییم تابع S ،f را برمیشمرد [برشمردن]. در S یک تابع پوشا، به فرض f، وجود داشته باشد. در این صورت میگوییم تابع S ،f را برمیشمرد [برشمردن].
☚ هر مجموعه متناهی شمارا است.
۱.۱۷.۱ شمارایی اعداد گویا/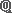 : : در جدول زیر اعداد گویای مثبت فهرست شدهاند(برشمرده شدهاند.) این نشان میدهد 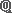 + شمارا است(به همین ترتیب + شمارا است(به همین ترتیب 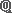 شمارا است و با توجه به شمارا است و با توجه به  ⊂ ⊂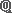 نامتناهی نیز است.) نامتناهی نیز است.) 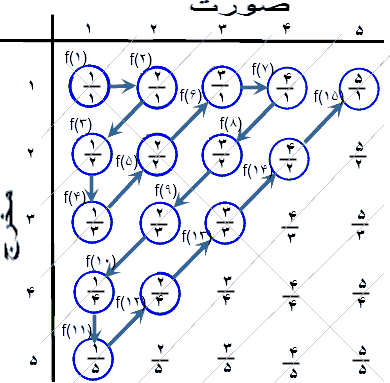
نمودار بالا همچنین نشان میدهد مجموعه  × × شمارا است و میتوان نشان داد که مجموعه همه nتاییهای مرتب اعداد طبیعی نیز شمارایند. شمارا است و میتوان نشان داد که مجموعه همه nتاییهای مرتب اعداد طبیعی نیز شمارایند. نیز نشان داده میشود که  ناشمارا است. روش اینگونه است که فاصله [a, b] برای مثال [۰, ۱] (که زیرمجموعه ناشمارا است. روش اینگونه است که فاصله [a, b] برای مثال [۰, ۱] (که زیرمجموعه  است) را در نظر گرفته و سپس تابت میکنند برای هر برشمارش این فاصله، عددی در این فاصله است که مشمول برشمارش نیست. سپس با توجه به اینکه "اگر مجموعهای دارای یک زیرمجموعه سره ناشمارا باشد خود ناشمارا است" به دست میآید است) را در نظر گرفته و سپس تابت میکنند برای هر برشمارش این فاصله، عددی در این فاصله است که مشمول برشمارش نیست. سپس با توجه به اینکه "اگر مجموعهای دارای یک زیرمجموعه سره ناشمارا باشد خود ناشمارا است" به دست میآید  ناشمارا است. کانتور به شیوهای موسوم به "برهان قطری کانتور/Cantor's diagonal argumentan" ناشمارایی ناشمارا است. کانتور به شیوهای موسوم به "برهان قطری کانتور/Cantor's diagonal argumentan" ناشمارایی  را نشان داد. را نشان داد.
۰.۱.۱۷.۱☚ چند خاصیت درباره مجموعههای شمارا: خاصیتهای زیر قابلاثبات هستند. ۱- حاصلضرب دکارتی هر تعداد محدود مجموعه شمارا، شمارا است.
۲- اجتماع هر تعداد محدود مجموعه شمارا، شمارا است.
۳- فرض کنید S یک مجموعه شمارا، آنگاه مجموعه همه زیرمجموعههای متناهی S شمارا است.
۴- مجموعه اعداد جبری شمارا هستند. [توضیح: عدد حقیقی a را عدد جبری گویند اگر ریشه یک چندجملهای با ضرایب صحیح باشد. نشان داده میشود اعداد گویا جبری هستند ولی همه اعداد حقیقی، برای مثال عدد π و عدد e جبری نیستند. به اعداد غیر جبری اعداد تراگذری گفته میشود.]
۱.۱.۱۷.۱ چه تعداد مجموعه نامتناهی وجود دارد؟ قضیه: نامتناهی مجموعه ناشمارای نامتناهی وجود دارد. اثبات: ابتدا ثابت میکنیم مجموعه توانی  ، یعنی Ƥ( ، یعنی Ƥ( ) ناشمارا و نامتناهی است. Ƥ( ) ناشمارا و نامتناهی است. Ƥ( ) را Pº مینامیم (به خاطر راحتی در نوشتن). روشن است Pº نامتناهی است و بنابراین فقط ثابت میکنیم Pº ناشمارا است. (توجه داریم که X∈Pº اگر و فقط اگر X⊆ ) را Pº مینامیم (به خاطر راحتی در نوشتن). روشن است Pº نامتناهی است و بنابراین فقط ثابت میکنیم Pº ناشمارا است. (توجه داریم که X∈Pº اگر و فقط اگر X⊆ .) .) ۱- میگوییم: گیریم تابع f :  ↦Pº وجود دارد به قسمی که Pº را برمیشمارد ↦Pº وجود دارد به قسمی که Pº را برمیشمارد (یعنی Pº شمارا است.) پس برای هر عضو Pº مانند X عدد طبیعی n هست به قسمی که: f(n)∈X. ۲- مجموعه (D⊆ ) ،D را به قسمی میگیریم که n∈D اگر و فقط اگر n∉f(n). ) ،D را به قسمی میگیریم که n∈D اگر و فقط اگر n∉f(n). ۳- ولی D∈Pº (چون D⊆ ) و طبق فرض(خلف) f همه اعضای Pº را برمیشمرد پس باید عددی طبیعی مانند d باشد کهf(d)=D . ) و طبق فرض(خلف) f همه اعضای Pº را برمیشمرد پس باید عددی طبیعی مانند d باشد کهf(d)=D . ۴- اما با توجه به ۲ برای هر n∈f(d) ؛n اگر و فقط اگر n∉f(n). و بنابراین بهویژه d∈f(d) اگر و فقط اگر d∉f(d)، که این یک تناقض و لذا فرض خلف باطل است. بنابراین Pº شمارا نیست و همینطور است برای Ƥ(Pº) و ادامه آن. ☚ ناشمارایی اعداد حقیقی: میتوان نشان داد فاصله دلخواه (a<b) [a, b]⊂ ناشمارا و بنابراین ناشمارا و بنابراین  ناشمارا است. ناشمارا است.
Axiom of choice,اصل موضوع انتخاب ۲.۱.۱۷.۱☚ اصل موضوع انتخاب اصل موضوع انتخاب، با کوته نویسیِ AC، توسط منطقی و ریاضیدان آلمانی ارنست زیمِلو ارائه گردیده. طبق این اصل اگر اعضای کلاسی، به فرض C، مجموعههای ناتهی باشند آنگاه مجموعهای هست که با هر یک از اعضای این کلاس دقیقاً یک عضو مشترک داشته باشد. بهعبارتدیگر، گیریم: C={X|X یک مجموعه ناتهی} [برای مثال Cمیتواند {X|X∈Ƥ( )} یا {{۱, ۲}, {۲, ۵, ۷}} و مانند آنها باشد.] )} یا {{۱, ۲}, {۲, ۵, ۷}} و مانند آنها باشد.] اصل موضوع انتخاب میگوید فرض وجود C منجر به وجود تابعی، به فرض f، از C در مجموعهای، به فرض Z، میگردد، به قسمی که، هر عضو Z انتخاب شده [به دست آمده] توسط تابع f از عضوهای عناصر C است. یعنی، برای هر X∈C داریم f(X)=z∈X که (z∈Z). تابع f در بالا را تابع انتخاب مینامند. درباره AC باید دانست: ۱- از اصل انتخاب به دست نمیآید چه گونه میتوان تابع انتخاب را ساخت [محاسبه کرد.] این اصل فقط مدعی وجود چنین تابعی آن است؛ ۲- چنانچه C متناهی باشد میتوان نشان داد تابع انتخاب وجود دارد و بنابراین در این حالت وجود تابع انتخاب موکول به پذیرش اصل موضوع انتخاب نیست؛ ۳- از اصل انتخاب میتوان نتیجه گرفت که هر مجموعه خوش-ترتیب شدنی است(ولی نمیگوید چگونه باید آن را خوش-ترتیب کرد.) این نتیجه به قضیه خوش-ترتیبی [همچنین به قضیه زیملو] معروف است. ۴- از قضیه خوش-ترتیبی میتوان اصل موضوع انتخاب را به دست آورد. به عبارت دیگر، این دو (خوش-ترتیب شدن و انتخاب کردن) همارز هستند. ☚ قضیه خوش-ترتیبی، شماره ۳ در بالا، متفاوت از اصل خوش-ترتیبی است.
۲.۱۷.۱ مقایسه پذیری مجموعهها آ: دو مجموعه، به فرض A و B، که اعضای آنها جفت شدنی باشند را همعدد میگویند. بهعبارتدیگر دو مجموعه همعدداند اگر بین آنها یک تناظر یکبهیک وجود داشته باشد(یعنی A⇌B.) ب: ب۱- گوییم A 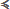 C B؛ اگر یک تابع یکبهیک، به فرض f، از A در B تعریف شده باشد. C B؛ اگر یک تابع یکبهیک، به فرض f، از A در B تعریف شده باشد. ب۲- بعلاوه گوییم A<CB؛ اگر f دو سویی نباشد. بهعبارتدیگر، A با یک زیرمجموعه B همعدد باشد ولی B با هیچ زیرمجموعه A همعدد نباشد. ☚ ازآنجاییکه تابع یکبهیک و ناپوشای f(x)=x از  در در  وجود دارد بنابراین: وجود دارد بنابراین:  <C <C . . ج: پرسش: آیا بهوسیله رابطه 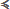 C هر دو مجموعه دلخواه مقایسه پذیراند؟ پاسخ آری است، اما قبل از آن باید چند قضیه را ثابت کرد و اصل انتخاب را نیز پذیرفت. در ادامه این قضایا و نتایج آنها را فهرست میکنیم. C هر دو مجموعه دلخواه مقایسه پذیراند؟ پاسخ آری است، اما قبل از آن باید چند قضیه را ثابت کرد و اصل انتخاب را نیز پذیرفت. در ادامه این قضایا و نتایج آنها را فهرست میکنیم.
۱.۲.۱۷.۱☚ قضیه کانتور د: قضیه کانتور: برای هر مجموعه دلخواه X داریم X <CƤ(X) . بهعبارتدیگر، یک تابع ۱:۱ (ولی نه هرگز دوسویه) از X در Ƥ(X) وجود دارد. اثبات: ۱- تابعg(x)={x} از X در Ƥ(X) را در نظر گرفته. آشکار است که این تابع ۱:۱ است. بنابراین داریم X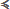 CƤ(X). میماند نشان دهیم تابعی از X در Ƥ(X)وجود ندارد که پوشا باشد. CƤ(X). میماند نشان دهیم تابعی از X در Ƥ(X)وجود ندارد که پوشا باشد. ۲- برای تابعی مانند f از X در Ƥ(X )، مجموعه A={x∈X|x∉f(x)} را در نظر بگیرید. (A چه تهی چه ناتهی باشد، زیرمجموعه X است و بنابراین تصویر عضوی از X تحت fخواهد بود.) ۳- فرض کنید برای عضوی از X مثل a داشته باشیم f(a)=A. ۴- فرض کنید a∈A . اما بنا بر ۳ داریم A=f(a) و لذا a∈f(a). بنابراین a∉A. ۵- فرض کنید a∉A . اما بنا بر ۳ داریم A=f(a) و لذا a∉f(a). بنابراین a∈A. ۶- از ۴ و ۶ داریم a∈A⇔ a∉A که آشکار یک تناقض است. بنابراین، A تصویر عضوی نیست.
۲.۲.۱۷.۱☚ قضیه شرودر برنشتاین گیریم A و B دو مجموعه، در این صورت داریم: A ⇌ B ⇐ B 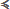 CA و A CA و A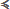 C B C B (توجه: اثبات این قضیه وابسته به پذیرش اصل انتخاب نیست.)
۳.۲.۱۷.۱☚ قضیه مقایسه پذیری: گیریم A و B دو مجموعه، در این صورت داریم: B 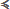 C A یا A C A یا A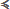 CB CB (توجه: اثبات این قضیه وابسته به پذیرش اصل انتخاب است.)
۴.۲.۱۷.۱☚ فرض پیوستار و کاردینال:جورج کانتور دو گزاره(حکم/conjecture) زیر را در سال ۱۸۷۸م بدون اثبات ارائه کرد: ۱.۴.۲.۱۷.۱☚ فرض پیوستار CH: هر زیرمجموعه ناشمارای  با  همعدد است. ۲.۴.۲.۱۷.۱☚ فرض پیوستار عام GCH: گیریم A یک مجموعه نامتناهی، آنگاه مجموعه B به قسمی که: A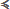 CB CB 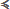 CƤ(A) CƤ(A) وجود ندارد. ۳.۲.۴.۲.۱۷.۱☚ فرض پیوستار عام همارز اصل موضوع انتخاب است، یعنی میتوان یکی را پذیرفت و دیگری را اثبات کرد. تفصیل را میتوان در این کتاب [*]-Gregory H. Moore;(1982) "Zermelo's Axiom of Choice Its Origins, Development, and Influence"; Springer-Verlag New York Inc. یافت.
۳.۴.۲.۱۷.۱☚ آیا فرضهای پیوستار درست هستند؟ هرآینه هنوز درستی یا نادرستی فرضهای پیوستار دانسته نیست. کورت گودل در ۱۹۳۰م نشان داد که فرض پیوستار در دستگاه ریاضیات(دستگاه اصل موضوعی ZF) قابل رد نیست و سپس ریاضیدان پل کوهن/Paul Cohen در ۱۹۶۰م نشان داد فرض پیوستار در همان دستگاه که قابل رد نیست، قابلاثبات نیز نیست. اصل موضوع انتخاب نیز چنین است. (در یادداشتهای منطق خواهیم دید که اگر فرمولی در یک دستگاه اصل موضوعی سازگار اثبات پذیر نباشد آنگاه نقیض آن را میتوان بدون خدشه به سازگاری به اصول موضوعه دستگاه افزود.)
۴.۴.۲.۱۷.۱☚ کاردینال و اعداد فراتر از بینهایت : اکنون با توجه به موارد بالا و اینکه: ۱- A⇌A
۲- A⇌B ⇒ B⇌A
۳- A⇌B , B⇌C ⇒ A⇌C میتوان به هر مجموعه مثل A نماد |A| را، که به آن کاردینال مجموعه A میگوییم، نسبت داد و گفت برای هر دو مجموعه A و B داریم؛ |A|=|B| ⇔ A⇌B بنا به فرض پیوستار کانتور مجموعهای که کاردینال آن بین کاردینال یک مجموعه و کاردینال مجموعه توانی آن باشد وجود ندارد. برای مثال اگر کاردینال مجموعه اعداد طبیعی، یعنی | |، را Xº و کاردینال مجموعه توانی آن یعنیƤ( |، را Xº و کاردینال مجموعه توانی آن یعنیƤ( ) را X۱ در نظر بگیریم آنگاه بنا بر قضیه کانتور، داریم Xº<CX۱ داریم [میگوییم Xº از X۱ کوچکتر و همینطور ) را X۱ در نظر بگیریم آنگاه بنا بر قضیه کانتور، داریم Xº<CX۱ داریم [میگوییم Xº از X۱ کوچکتر و همینطور  از Ƥ( از Ƥ( ) (بهطور کاردینالی) کوچکتر است] و نیز بنا به فرض پیوستار کانتور کاردینال دیگری بین Xº و X۱ وجود ندارد. ) (بهطور کاردینالی) کوچکتر است] و نیز بنا به فرض پیوستار کانتور کاردینال دیگری بین Xº و X۱ وجود ندارد. این روند را میتوان برای Ƥ(Ƥ( )) و Ƥ(Ƥ. . .Ƥ(Ƥ ( )) و Ƥ(Ƥ. . .Ƥ(Ƥ ( )). . .) ادامه داد و نوشت: )). . .) ادامه داد و نوشت: Xº < X۱< X۲<. . . <Xn . . . و چنین مفروض دانست که بین (i∈ ∪{0}) Xi+۱ و Xi کاردینال دیگری وجود ندارد. ∪{0}) Xi+۱ و Xi کاردینال دیگری وجود ندارد. در ریاضی از نماد ℵ(الف/Alef) بهجای X استفاده میشود و با توجه به آنچه گفته شد میتوان دنباله زیر را داشت. ℵº, ℵ۱, . . .,ℵn, . . . به عناصر این دنباله کاردینال نامتناهی یا اعداد ترانسفینی میگویند.
۵.۲.۱۷.۱☚ کاردینال مجموعههای متناهی نماد کاردینال مجموعه تهی را 0º (یا ۰) و کاردینال مجموعههای n عضوی ر nº (یا n) میگیریم. در این صورت با توجه به ۱.۱۶.۲ ℵº کوچکترین عدد ترانسفینی است که از کاردینال هر مجموعه متناهی بزرگتر است.
۶.۲.۱۷.۱☚ پارادوکس کانتور ۱-گیریم U مجموعه شامل همه اشیاء (چه مجموعه چه غیر مجموعه) از جمله خود باشد(موسوم به مجموعه جهانی.) طبق قضیه کانتور : |U |<| Ƥ(U)|. ۲- از طرفی بنا به تعریف U داریم Ƥ(U )⊂U. پس بهموجب قضیه کانتور: Ƥ(U)| ≤|U|. ۳-اکنون بنا به قضیه شرودر-برنشتاین از (۱) و (۲) خواهیم داشت: |U| =|Ƥ(U)|. نتیجه اخیر متناقض با |U| <|Ƥ( U)| است. این پارادوکس به پارادوکس کانتور موسوم است.
۱۸.۱ دنباله فرض کنید S مجموعه و D یک زیرمجموعه  * باشد. به یک تابع از D در S یک دنباله گفته میشود. اگر S⊆ * باشد. به یک تابع از D در S یک دنباله گفته میشود. اگر S⊆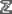 باشد دنباله را صحیح و اگر S⊆ باشد دنباله را صحیح و اگر S⊆ باشد دنباله را حقیقی گویند. باشد دنباله را حقیقی گویند. برای مثال، اگر S={a, c, f}؛ آنگاه تابع u در زیر یک دنباله را تعریف میکند. u : {۱, ۲, ۳} ↦ S; | تعریف دنباله u | | ۳ | ۲ | ۱ | e∈U | | u۳=a | u۲=a | u۱=c | u(e)∈S | | به u۱, u۲, u۳ عناصر دنباله U۳ میگویند. |
ازآنجاکه مجموعه عزیمت یک دنباله همیشه زیرمجموعه  است، معمولاً عناصر یک دنباله را بهصورت: v1, v2, . . ., vn یا <v1, v2, . . ., vn> نمایش میدهند تا بتوان به عنصر خاصی از دنباله با توجه به موقعیت آن اشاره کرد. وقتی مجموعه عزیمت دنباله است، معمولاً عناصر یک دنباله را بهصورت: v1, v2, . . ., vn یا <v1, v2, . . ., vn> نمایش میدهند تا بتوان به عنصر خاصی از دنباله با توجه به موقعیت آن اشاره کرد. وقتی مجموعه عزیمت دنباله  باشد دنباله را نامتناهی گفته. عناصر یک دنباله نامتناهی را معمولاً با جمله عمومی دنباله تعریف میکنند. در زیر چند مثال از دنباله نامتناهی آمده است: باشد دنباله را نامتناهی گفته. عناصر یک دنباله نامتناهی را معمولاً با جمله عمومی دنباله تعریف میکنند. در زیر چند مثال از دنباله نامتناهی آمده است: | دنباله | جمله عمومی | | <۱, ۴, ۸, . . .> | Un=n۲ | | <۱, ۲, ۶, . . .> | Vn=۱×۲×...×n |
بهآسانی میتوان دریافت که هر فهرست از اعداد نشاندهنده یک دنباله(تابع) است.
۱۹.۱ استقرا در ریاضی: ۱.۱۹.۱ اصل استقرای ریاضی: اصل استقرای ریاضی: گیریم خاصیت P برای عدد ۰ برقرار است و هرگز برای هر عدد طبیعی n برقرار نخواهد بود مگر آنکه برای n+۱ برقرار باشد. در این صورت P برای همه اعداد طبیعی برقرار خواهد بود. ۲.۱۹.۱ استقرای کامل: استقرای کامل: گیریم خاصیت P برای هر عدد طبیعی n وقتی برقرار است که برای همه اعداد طبیعی کوچکتر از n برقرار باشد؛ آنگاه P برای همه اعداد طبیعی برقرار است. ☚ . اصل استقرای ریاضی و استقرای ریاضی کامل دو بیان متفاوت و همارز هستند، یعنی با فرض یکی دیگری را میتوان اثبات کرد. همچنین اصل خوشترتیبی اعداد طبیعی (هر زیرمجموعه ناتهی اعداد طبیعی دارای کوچکترین عنصر است) با اصل استقرای ریاضی همارز است. ☚ . همچنین گیریم خاصیت P برای ۱ برقرار و اگر برای عدد طبیعی n برقرار، برای n+۱ نیز برقرار است؛ آنگاه P برای همه اعداد طبیعی برقرار است.
۲۰.۱ دنبالهها، مجموعهها و توابع بازگشتی ۱.۲۰.۱ دنبالههای بازگشتی بعضی دنبالهها را میتوان به روشی موسوم به بازگشتی تعریف کرد. مزیت این نوع تعریف آن است که تعریف مفهومی و تعریف مصداقی را توأم ارائه میکند و ازاینجهت به آن تعریف سازنده (بناکننده) نیز میگویند. تعریف بازگشتی دنباله در سه گام انجام میشود ۱- (گام مبنایی) یک یا تعداد محدود از عناصر دنباله معرفی میشود؛ ۲- (گام استقرایی) اعمالی معرفی که بهموجب آن اعمال عنصری از دنباله برحسب عناصر موجود (فعلی) دنباله حاصل میگردد؛ ۳- (گام نهایی) تأکید میشود که فقط آنچه از دو مرحله ساخت ۱ و ۲ حاصل میشود عنصر دنباله است و نه هیچچیز دیگر. در مثالی که میآید دنبالهای بنام Fin را به روش بازگشتی میسازیم. در گام اول میگویی ۱ و ۱ ازجمله عناصر این دنباله هستند. در گام دوم میگوییم اگر Fik و Fik-۱ عناصر این دنباله باشند آنگاه Fik-۱+Fik نیز عنصر این دنباله است. در گام سوم میگوییم فقط آنچه از دو گام اول ساخته میشود عنصر Fin است. در زیر تعدادی عناصر اولیه این دنباله آمده است: | <Fi۱, | Fi۲, | Fi۳, | Fi۴, | Fi۵, | Fi۶, | Fi۷, . . .> | | <۱, | ۱, | ۲, | ۳, | ۵, | ۸, | ۱۳, . . .> | | <۱ | ۱ | ۱+۱=۲ | ۱+۲=۳ | ۲+۳=۵ | ۳+۵=۸ | ۵+۸=۱۳, . . .> |
۲.۲۰.۱ مجموعههای بازگشتی بعضی مجموعهها را میتوان به روش بازگشتی مشابه با آنچه درباره دنبالهها گفتیم تعریف کرد. مجموعهای که به روش بازگشتی قابلتعریف باشد به مجموعه بازگشتی موسوم است. هر مجموعه بازگشتی در سه گام به شرحی که میآید تعریف میشود: ۱- (گام مبنایی) یک یا تعداد محدودی از اعضای مجموعه معرفی میشود؛ ۲- (گام استقرایی) اعمال (یا قواعدی) معرفی که بهموجب آنها عضوی از مجموعه برحسب اعضای موجود (فعلی) مجموعه ساخته میشود؛ ۳- (گام نهایی) تأکید میشود که فقط آنچه از دو مرحله ساخت ۱ و ۲ ساخته شود عضو مجموعه است و نه هیچ عنصر دیگر. فرض کنید میخواهیم مجموعهای بنام N را به روش بازگشتی تعریف کنیم. ۱- در گام مبنایی میگوییم: ۰∈N؛ ۲- در گام استقرایی میگوییم: اگر x∈N آنگاه x+۱∈N؛ ۳- در گام نهایی میگوییم: فقط و فقط آنچه از ۱ و ۲ حاصل میشود عضو N است. به ۰ عنصر سازنده/مولد مجموعه N گفته میشود و میتوان دید N همان 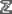 + است. بنابراین مجموعه اعداد طبیعی یک مجموعه بازگشتی است. + است. بنابراین مجموعه اعداد طبیعی یک مجموعه بازگشتی است. برای مثال دیگر فرض کنید میخواهیم مجموعهای بنام N' را به روش بازگشتی تعریف کنیم. ۱- در گام مبنایی میگوییم ۰∈N'. ۲- در گام استقرایی ابتدا تابع s را در N' به قسمی تعریف میکنیم که s(x) مخالف ۰ و نیز مخالف اعضای تاکنون ساختهشده در N' باشد و میگوییم اگر x∈N' باشد آنگاه s(x)∈N'. ۳- در گام نهایی میگوییم: فقط و فقط آنچه از ۱ و ۲ حاصل میشود عضو N' است. بنابراین N'={۰, s(۰), s(s(۰)), s(s(s(۰))), . . .}. ◄ . به تابعی با کارکرد تابع s در بالا تابع تالی [پی-آمد] گفته و آن را معمولاً با succ نشان داده. در این مثال میتوان نوشت:succ(n)=n+1 . برای مثال دیگر فرض کنید میخواهیم مجموعهای بنام N'' را به روش بازگشتی تعریف کنیم. ۱- در گام مبنایی میگوییم: ø∈N''. ۲- در گام استقرایی میگوییم: اگر x∈N'' باشد آنگاه x∪{x}∈N''. [در اینجا succ(x)=x∪{x}.] ۳- در گام نهایی میگوییم: فقط و فقط آنچه از ۱ و ۲ حاصل میشود عضو N'' است. بنابراین N''={ø, ø∪{ø}={ø}, {ø}∪{{ø}}={ø, {ø}}, {ø, {ø},{ø,{ø}}}, . . . }. اگر در این مثال ø را با نماد ۰، {ø} را با ۱، {ø, {ø}} را با ۲ نشان دهیم و همینطور مانند آنها، آنگاه مجموعه {۰, ۱, ۲, . . .} را در پی خواهیم داشت که ø مولد/سازنده آن است. این روشی بود که ریاضیدان و منطقی ایتالیایی جوزپه پینو (Giuseppe Peano-۱۸۵۸-۱۹۳۵) (بسیار مورد تحسین برتراند راسل) در دستگاه اصل موضوعی اعداد به کاربست.
۳.۲۰.۱ توابع بازگشتی ازآنجاکه توابع مجموعه هستند، توابع بازگشتی را نیز میتوان به همان سیاق مجموعههای بازگشتی تعریف کرد. توابع بازگشتی ازجمله در دانش کامپیوتر (الگوریتم، ماشین، محاسبهپذیری، هوش مصنوعی و جاهای دیگر) دارای اهمیت اساسی هستند. در یک رهیافت (رهیافت موسوم به آلونزو چرچ/Alonzo Church: ریاضیدان و منطقی آمریکایی- ۱۹۹۵-۱۹۰۳) یک روند را کارآمد (الگوریتم-روش مکانیکی) گوییم اگر قابلبیان توسط تعداد محدود توابع بازگشتی باشد. در هنگام بحث الگوریتم و ماشین به این بحث باز میگردیم.
۲۱.۱ رشته و زبان: فرض کنید Σ مجموعهای ناتهی باشد. پس از تعیین این مجموعه، آن را الفبا و اعضای آن را حروف الفبا مینامیم. بناشده بر Σ مجموعه دیگری را معرفی میکنیم و اعضای آن را رشته مینامیم. این کار را در دو گام انجام میدهیم. در گام اول دنباله مجموعه: <Σ, Σ1, ..., Σn , ...> را بر پایه Σ میسازیم. در گام دوم تعریف مجموعه موردنظر را تمام میکنیم. گام یکم: Σ۱=Σ
Σ۲={xy|x∈Σ, y∈Σ۱}
Σ۳={xy|x∈Σ, y∈Σ۲}
................
................
Σn={xy|x∈Σ, y∈Σn-1}
................
................ | Σ={1, 0}
Σ۱={0, 1}
Σ۲={ 00, 01, 10, 11}
Σ۳={000,001,010,011,100,101,000,001}
................
Σn={00...0,00...1, . . ., 11...1}; |Σn|=۲n.
................
................ | مثال: |
گام دوم: اجتماع مجموعههای Σ, Σ1, . . ., Σn , . . . را +Σ مینامیم و به اعضای +Σ رشته میگوییم. مثال: اگر Σ را ارقام ۱ تا ۹ بگیریم آنگاه Σ+ (یا رشتهها) اعداد طبیعی بدون رقم صفر خواهند بود. اگر Σ را حروف فارسی بگیریم آنگاه Σ+ عبارات ممکن(بامعنی و بیمعنی، محدود و نامحدود) فارسی خواهد بود. و سرانجام اگر Σ را مجموعه Σ={p, q, ~, •, ∨,⊃, ≡, (, )} باشد آنگاه p∨r ; ~pq))))))(q•∨⊃ ; p⊃(p∨q) هریک رشتههای حاصل از الفبای Σ هستند. ◄ . مجموعه +Σ همیشه یک مجموعه نامتناهی است؛ حتی اگر Σ فقط یک عضو داشته باشد. ◄ . اگر Σ شمارا باشد با توجه به خواص شمارایی، +Σ و نیز هر زیرمجموعه +Σ شمارا است. ◄ . مرسوم است نماد 'Λ' بهعنوان یک حرف الفبا به نام خالی برای هر Σ (الفبا) در نظر بگیرند. ۱.۲۱.۱ پاره(یا قطعه) آغازی رشته: اگر S=s۱s۲...sn یک رشته باشد، آنگاه به S'=s۱s۲...sm که در آن ۰≤m≤n یک پاره آغازی S میگوییم. اگر ۰<m<n به S' یک پاره آغازی سره S و اگر m=۰ به S' پاره آغازین خالی S' میگوییم. بنابراین میتوان از یک رشته با پاره آغازین خاصی نام برد. ۲.۲۱.۱ پاره پایانی رشته: اگر S=s۱s۲...sn یک رشته باشد، آنگاه به S'=smsm+۱...sn که در آن ۰≤m≤n یک پاره پایانی S میگوییم. اگر ۰<m<n به S' یک پاره پایانی سره S و اگر m=۰ به S' پاره پایانی خالی S' میگوییم. بنابراین میتوان از یک رشته با پاره پایانی خاصی نام برد. ۳.۲۱.۱ الحاق رشتهها: اگر S=s۱s۲...sn و S'=s'۱s'۲...s'n رشته باشند، به s۱s۲...sns'۱s'۲...s'm رشته حاصل از الحاق رشته S با S' گفته میشود. معمولاً عملگر الحاق را با  نشان میدهند. بنابراین: نشان میدهند. بنابراین: S S'=s۱s۲...sns'۱s'۲...s'm S'=s۱s۲...sns'۱s'۲...s'm ۴.۲۱.۱ عبارت و طول عبارت: به رشتههای متناهی عبارت میگویند. اگر t یک عبارت باشد آنگاه طول عبارت را برابر تعداد الفبای بهکاررفته در آن میگیریم. طول رشته t را با |t| نشان میدهیم. بنابراین در آخرین مثال داریم؛ |p∨r|=۳. ☚ .طول Λ (عبارت خالی) را همیشه برابر صفر فرض میکنیم و نباید آن را با فاصله خالی(در صورت آنکه الفبا چنین حرفی را داشته باشد) یکی فرض کرد. برای مثال داریم: |aΛbΛ|=|ab|=۲. ☚ .مجموعه عبارات . ۵.۲۱.۱ زبان: در تمام آنچه در این بند آمد اگر بهجای واژه الفبا عبارت واژگان ابتدایی را بهکاربرده آنگاه به +Σ یک زبان با واژگان ابتدایی Σ گفته میشود.
۲۲.۱ اعداد اردینال: خواهد آمد...
| 
جرج کانتور(۱۹۱۸-۱۸۴۵) /Georg Cantor ریاضیدان آلمانی و بانی نظریه مجموعهها

ارنست زیملو(۱۹۵۳-۱۸۷۱) /Ernst Zermelo منطقی، ریاضیدان آلمانی و واضع دستگاه اصل موضوعی ZFC.
|
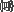 "باشد. اکنون میتوان گفت
"باشد. اکنون میتوان گفت 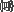 نام یک مجموعه است و تعریف
نام یک مجموعه است و تعریف 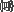 (تعریف مجموعه
(تعریف مجموعه 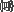 و نه تعریف مجموعه) میتواند "چیزهایی که پرویز در مسیر روزانه رساندن فرزند خود به مدرسه میبیند" باشد. به هر یک از این چیزها گفته که یک عضو
و نه تعریف مجموعه) میتواند "چیزهایی که پرویز در مسیر روزانه رساندن فرزند خود به مدرسه میبیند" باشد. به هر یک از این چیزها گفته که یک عضو 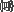 هستند [یا عنصر
هستند [یا عنصر 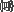 هستند یا در
هستند یا در 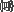 هستند، یا تعلق به
هستند، یا تعلق به 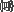 دارند.]
دارند.]  را
را 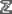 را نشان دارد بهقرار {. . . ،۲ ، ۱، ۰، ۱-، ۲-، .. . .} است.
را نشان دارد بهقرار {. . . ،۲ ، ۱، ۰، ۱-، ۲-، .. . .} است. 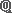 را نشان دارد. این مجموعه همه عضوهای
را نشان دارد. این مجموعه همه عضوهای 
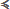
 f
f

