تساوی و اینهمانی (۱)
منطق محمولات و نظریه مدل
درآمد به منطق و رایانش
منطق
محمولات: تساوی و اینهمانی (۱)
۱- | ۷- تمرین (۲.۶۶ - ۲.۶۸) |
۲- تئوری مرتبه اول (همراه) با تساوی | ۸- (۲.۶۶) تئوری تساوی مرتبه اول محض |
۳- (۲.۲۳) قضیه (۳ ویژگی تساوی) | ۹- دو مثال: تئوری گروه‌ها و تئوری میدان‌ها |
۴- تمرین (۲.۶۴ - ۲.۶۵) | ۱۰- تئوری مقدماتی گروه‌ها (G) |
۵- (۲.۲۴) قضیه. (تحت شرایط خاص، تساوی اتمی به معنای تساوی کامل در یک تئوری است.) | ۱۱- تئوری مقدماتی میدان (F) |
۶- (۲.۲۵) قضیه. [دو شرط برای حذف بنداشت (A۷)] | ۱۲- تمرین (۲.۶۹) |
مگر در مواردی که با نماد "" مشخص شده باشد، محتوای ارائه شده در این یادداشت از مرجع زیر برگرفته و برگردان شده است.
Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. p. ۹۳-۹۸. ↜
۱- مراد از مجموعه شمارا (Denumerable set) یک مجموعه شمارای نامتناهی است مگر آنکه با صراحت قید شده باشد.
⦿ (تساوی و اینهمانی)■ تساوی و اینهمانی
در این قسمت و بعدی آن با تئوری‌های مرتبه-اول (همراه) با تساوی (=) و رویکرد بنداشتی با آن مواجه می‌شویم (مندلسون، مقدمه به منطق ریاضی، ۲۰۱۵، ص ۹۳). بنابراین، جا دارد ابتدا توضیح مختصری از محمول تساوی (Equality) و ارتباط آن با انگاست اینهمانی (Identity) آنگونه که در زبان طبیعی درک می‌شود، ارائه شود.
در نگاه اول و البته بنیادی، تساوی از این جهت که حرف محمولی (دو جایبانی) است جای آن در زبان صوری (نحو) است. از جهت دیگر، اینهمانی یک رابطه است که می‌تواند تعبیر (معنا) حرف محمولی در یک دامنه تعبیر باشد. در حالی که این دو اغلب به جای یکدیگر در زبان طبیعی به کار می‌روند، اما در منطق، آنها مفاهیم متمایز و در عین حال مرتبط هستند. توضیحی که می‌آید شاید بتواند در شکافتن بیشتر این موضوع کمک کند.
در واقع اینهمانی بیان قوی‌ترین پیوند ممکن بین دو چیز است. وقی می‌گوییم الف همان ب است، می‌گوییم الف و ب نه تنها ویژگی‌های یکسان دارند بلکه آنها یک هستی‌مند (موجودیت) یکسان هستند. برای مثال، ستاره بامدادی و ستاره شام گاهی را در نظر بگیرید. هر دو این نام‌ها، با وجود توصیف متفاوت، به سیاره ناهید رجوع دارند. یعنی هر دو به یک جرم آسمانی رجوع داردند که در زمان‌های مختلف دیده می‌شود.
یک اصل اساسی مرتبط با اینهمانی، قانون لایب نیتس (نیز نامیده به اصل اینهمانی تمایزناپذیرها) است. بنا به این اصل: اگر هر خاصیتی که `x` دارد، `y` نیز داشته باشد آنگاه `x` و `y` این‌همان هستند، و نیز وارون آن.
این اصل را می‌توان به صورت زیر پیکربندی کرد، که در آن `P` یک ویژگی است:
۱- تمایزناپذیریِ این‌همانی‌ها: اگر دو موجودیت این‌همان باشند (یعنی یک چیز هستند)، آنگاه همه ویژگی‌ها را به اشتراک می‌گذارند. یعنی، اگر `x` و `y` یک شی باشند، هیچ ویژگی نمی‌تواند آنها را متمایز کند. و بطور صوری:
(a) `x=y⇒(∀P)(P(x)⇔P(y))`
۲- این‌همانیِ تمایزناپذیرها: اگر دو موجودیت همه ویژگی‌ها را به اشتراک بگذارند، این‌همان هستند. یعنی، شباهت کیفی کامل به معنای اینهمانی عددی دارند. و بطور صوری:
(b) `(∀P)(P(x)⇔P(y)) ⇒ x=y`
توجه داریم که قانون لایب نیتس گسترشی است. یعنی این قانون در مورد ویژگی‌های عینی (برای مثال، جرم، مکان) اعمال می‌شود، نه ویژگی‌های ذهنی یا معرفت شناختانه (برای مثال، "باور بر این است که . . .."). حتی اگر داشته باشیم `x = y`، ممکن است کسی نداند که `x = y`. بنابراین ویژگی "باور بر این است که `x` ... است" می‌تواند برای `x`، اما نه `y` اعمال شود. این موجب نقض قانون لایب نیتس نیست، زیرا چنین ویژگی‌های معرفتی به معنای مربوط به این زمینه "واقعی" نیستند(*). در واقع، دستگاه‌های صوری معمولاً به انتزاع جنبه‌های معرفتی (Epistemic)، یعنی اینکه ما چگونه به کشف این‌همانی‌ها دست می‌یابیم، می‌پردازد و در منطق صرفاً متمرکز بر وضع بودگی (Ontic) آنها، یعنی آن چه این‌همانی‌ها هستند، تمرکز داریم.
(*):
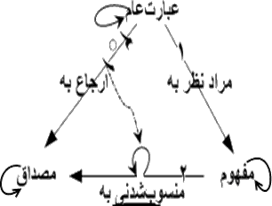
مثلث معنایی / Semiotic triangle
نکته اینکه در نزد فرگه به‌گونه‌ای `a=b` اینهمانی (به عنوان مرجع / چیز مورد اشاره) و تساوی (به عنوان ادعای مرجع مشترک) یکی در نظر گرفته می‌شوند، و تنها در مورد دوم است که از نظر شناختی (Cognitive) قابل توجه است.↝ این دوگانگی بازتاب دهنده جدایی نماد، مفهوم و مرجع (مصداق) در مثلث نشانه شناسی است. (نظریه معنی فرگه)
پابرجایی کریپکه Kripke’s Rigidity
از دیدگاه فیلسوف و منطق‌دان کریپکی↝-↝ نام‌های خاص (Proper Names) از یک شی آن را به شیوه پابرجا (Rigidly) در جهان‌های ممکن مشخص می‌کنند. یعنی `a=b` در همه تعبیرها درست است یا در همه تعبیرها نادرست است.
در زیر دو استدلال البته معیوب الف و ب آمده است. توجه به جنبه‌های خطایی آنها شاید بتواند روشن کننده باشد.
الف:
۱. سعدی وجود دارد.
۲. سعدی همان سراینده بوستان است.
۳. بنا به (Kripke’s Rigidity)، سعدی در هر تعبیر ممکن (عالم ممکن) سراینده بوستان است.
۴. (نتیجه): سعدی در هر تعبیر ممکن (عالم ممکن) وجود دارد.
ب:
۱. سعدی وجود دارد.
۲. سعدی همان سراینده بوستان است.
۳. سعدی ضرورتاً سراینده بوستان است.
۴. (نتیجه): سعدی به ضرورت وجود دارد.
1. https://en.wikipedia.org/wiki/Saul_Kripke
2. https://plato.stanford.edu/entries/rigid-designators/
3. Kripke, Saul A. (1980). Naming and Necessity: Lectures Given to the Princeton University Philosophy Colloquium. Cambridge, MA: Harvard University Press. Edited by Darragh Byrne and Max Kölbel.
4. Frege, Gottlob (1892). Uber Sinn und Bedeutung (On sense and Reference). Zeitschrift für Philosophie Und Philosophische Kritik 100 (1):25-50.
این‌همانیِ تمایزناپذیرها، همانطور که در (b) دیده می‌شود، وابسته به سور روی همه ویژگی‌ها `(AAP)` است (`P` یک ویژگی است). در منطق مرتبه-اول سورها `(AA, EE)` به متغیرهای انفرادی محدود هستند. در نتیجه، فرمول (b) در چارچوب منطقی عمل می‌کنند که بالاتر از توان گویایی منطق مرتبه-اول است. به عبارت دیگر، (b) در بالا به زبان صوری بالاتر از مرتبه-اول بیان شده‌اند. بنابراین، وسعت کامل اصل این‌همانیِ تمایزناپذیرها را نمی‌توان در منطق مرتبه-اول به تصویر کشید. بنابراین برای صوری کردن قانون لایب نیتس بطور کامل، حداقل به منطق مرتبه-دوم یا نظریه مجموعه‌ها نیاز است (جایی که ویژگی‌ها را می‌توان به عنوان مجموعه بازنمایاند).
در بحث تئوری‌های مرتبه اول (همراه) با تساوی خواهیم دید چگونه حرف محمولی تساوی (=)، در منطق مرتبه-اول به طور صوری معرفی و بنداشتی می‌شود. و چگونه این بنداشت‌ها تضمین می‌کنند که رفتار آن (=) به گونه‌ای باشد که با شهود ما درباره یکسانی در دستگاه‌های صوری (برای مثال برای مقاصد کاربردی در ریاضی و علوم کامپیوتر) مطابقت داشته باشد.
در واقع، طرح‌واره‌های بنداشتی تساوی (A۶) - (A۷)، که در ادامه خواهیم دید، تضمین می‌کنند که = نسبت به ویژگی‌های قابل بیان زبان (در اینجا زبان K) به‌عنوان اینهمانی رفتار می‌کند. اما، چنین دستگاهی نمی‌تواند تضمین کند که دو شی که تمام ویژگی‌های مرتبه-اول را به اشتراک می‌گذارند این‌همان هستند.
■ تئوری مرتبه اول (همراه) با تساوی
فرض کنید K تئوری‌ای باشد که یکی از حروف محمولی آن `A_۱^۲` باشد. `t=s` را به عنوان کوته‌شده `A_۱^۲(t,s)` و `t≠s` را به عنوان کوته‌شده `¬A_۱^۲(t,s)` بگیرید. اکنون به K یک تئوری مرتبه اول با تساوی (یا فقط یک تئوری با تساوی) گفته می‌شود اگر موردهای زیر قضیه‌های K باشند:
| (A۶): `(∀x_۱)x_۱ = x_۱` | (بازتابی بودن تساوی) |
| (A۷): `x= y⇒ (cc"B" (x, x) ⇒ cc"B" (x, y))` | (جایگزینی بودن تساوی) |
که در آن `x` و `y` می‌توانند هر متغیری باشند و `cc"B"(x, x)` یک فرمول است. `cc"B"(x, y)` از `cc"B"(x, x)` با جایگزینی برخی، اما نه لزوماً همه، رویدادهای آزاد `x` با `y`، با این قید که `y` برای `x` در `cc"B"(x,x)` آزاد است ناشی می‌شود. بنابراین، `cc"B"(x, y)` ممکن است حاوی رویدادهای آزاد `x` باشد یا نباشد. شماره گذاری (A۶) و (A۷) ادامه شماره گذاری بنداشتهای منطقی است.
■ ۲.۲۳ قضیه (۳ ویژگی تساوی)
برای هر تئوری با تساوی دایم:
a. `⊢ t = t`(برای هر ترم `t`)
b. `⊢ t = s ⇒ s = t` (برای هر ترم `t` و `s`)
c. `⊢ t = s ⇒ (s = r ⇒ t = r)` (برای هر ترم `t`، `s` و `r`)
اثبات:
(b):
فرض کنید `x` و `y` متغیرهایی باشند که در `t` یا `s` وجود ندارند. `cc"B"(x, x)` را از قرار `x = x` و `cc"B"(x, y)` را از قرار `y = x` در طرحواره (A۷)، `⊢ x = y ⇒ (x = x ⇒ y = x)` می‌گیرم.
اما، بنا بر (a) می‌نویسیم `⊢ x = x`. بنابراین، با موردی از توتولوژی
`(A ⇒ (B ⇒ C)) ⇒ (B ⇒ (A ⇒ C))`
و دو کاربرد MP به `⊢ x = y ⇒ y = x` می‌رسیم.
دو کاربرد تعمیم `⊢ (∀x)(∀y) (x = y ⇒ y = x)` را بدست می‌دهد. سپس با دو کاربرد قاعده A۴ خواهیم داشت ⊢ `t = s ⇒ s = t`.
(c):
فرض کنید ، `y` و `z` سه متغیر باشند که در `t`، `s` یا `r` وجود ندارند.
`cc"B"(y، y)` را عبارت از `y = z` و `cc"B"(y، x)` را عبارت از `x = z` در (A۷) بگیرید.
با جابجایی `x` و `y` با یکدیگر خواهیم داشت `⊢ y = x ⇒ (y = z ⇒ x = z)`.
اما، از (b) داریم `⊢ x = y ⇒ y = x`.
از این رو، با کارگرفتن موردی از توتولوژی
`(A ⇒ B) ⇒ ((B ⇒ C) ⇒ (A ⇒ C))`
و دو کاربرد MP به `⊢ x = y ⇒ (y = z ⇒ x = z)` خواهیم رسید.
با سه کاربرد Gen می‌رسیم به ` ⊢ (∀x)(∀y)(∀z)(x = y ⇒ (y = z ⇒ x = z))`.
سپس با سه بار کارزدن قاعده A۴ خواهیم داشت `⊢ t = s ⇒ (s = r ⇒ t = r)` .
■ تمرین (۲.۶۴ - ۲.۶۵)
۲.۶۴. نشان دهید که (A۶) و (A۷) برای هر تعبیر M بقسمی که `(A_1^2)^M` [ یعنی، معنی حرف محمولی `A_1^2` تحت تعبیر M] رابطه اینهمانی در عالم سخن است، درست هستند.
۲.۶۵. نشان دهید موردهای زیر تحت هر تئوری با تساوی برقرارند.
| a. `⊢(∀x)(cc"B"(x)⇔(∃y)(x = y ∧ cc"B"(y)))` | اگر `y` در `cc"B"(x)` دارای رویداد نباشد. | |||||||||
| b. `⊢ (∀x)(cc"B" (x) ``⇔ (∀y)(x = y ⇒ cc"B" (y)))` | اگر `y` در `cc"B"(x)` دارای رویداد نباشد. | |||||||||
| c. `⊢ (∀x)(∃y)x = y` | ||||||||||
| حل: | ||||||||||
| ||||||||||
| d. `⊢ x = y ⇒ f(x) = f(y)` | که در آن `f` حرف تابعی یک آرگومانی (یک متغیری) است. | |||||||||
| e. `⊢ cc"B" (x) ∧ x = y ⇒ cc"B" (y)` | اگر `y` برای `x` در `cc"B"(x)` آزاد است. | |||||||||
| f. `⊢ cc"B" (x) ∧ ¬cc"B" (y) ⇒ x ≠ y` | اگر `y` برای `x` در `cc"B"(x)` آزاد است. | |||||||||
■ ۲.۲۴ قضیه. (تحت شرایط خاص، تساوی اتمی به معنای تساوی کامل در یک تئوری است)
(قضیه) فرض کنید K یک تئوری باشد که برای آن (A۶) برقرار باشد و (A۷) برای همه فرمول‌های اتمی `cc"B"(x, x)` که در آن هیچ ثابت انفرادی وجود ندارد، برقرار است. در این صورت K یک تئوری با تساوی است، یعنی (A۷) برای همه فرمول های `cc"B"(x, x)` برقرار است.
اثبات:
باید (A۷) را برای همه فرمول‌های `cc"B"(x,x)` ثابت کنیم.
این برای فرمول‌های اتمی بر اساس فرض برقرار است. توجه داشته باشید که ما نتایج قضیه ۲.۲۳ را داریم، که در اثبات آن (A۷) فقط با فرمول های اتمی بدون ثابت انفرادی بکار زده شده است.
همچنین توجه داشته باشید که ما (A۷) را برای همه فرمول‌های اتمی `cc"B"(x,x)` داریم. زیرا اگر `cc"B"(x,x)` دارای ثابت‌های انفرادی باشد، می‌توانیم آن ثابت‌های انفرادی را با متغیرهای جدید جایگزین کنیم و فرمول `cc"B"^**(x,x)` را بدون ثابت‌های انفرادی به دست آوریم.
طبق فرض، مورد متناظر (A۷) با `cc"B"^**(x,x)` یک قضیه است. پس می‌توانیم Gen را با توجه به متغیرهای جدید اعمال کنیم و در نهایت قاعده A۴ را یک یا چند بار برای به دست آوردن (A۷) با توجه به `cc"B"(x,x)` اعمال کنیم.
با استقرا روی `n` تعداد رابط‌ها و سورها در `cc"B"(x,x)` اثبات را پیش می‌بریم. فرض می‌کنیم که (A۷) برای همه `k< n` برقرار است.
حالت ۱. `cc"B" (x, x)` بصورت `¬cc"C" (x, x)` است.
با فرض استقرا داریم:
`⊢ y = x ⇒ (cc"C" (x, y) ⇒ cc"C" (x, x))`
زیرا `cc"C" (x, x)` با جایگزینی برخی از رویدادهای `y` با `x` از `cc"C" (x ، y)` حاصل می‌شود. از این رو، با قضیه .۲.۲۳.a و موردهایی از توتولوژی‌های
`(A⇒B)⇒(¬B⇒¬A)` و `(A⇒B)⇒(B⇒C)⇒(A⇒C))`
و MP خواهیم داشت: `⊢x=y ⇒ (cc"B"(x, x) ⇒ cc"B"(x, y))`.
حالت ۲. `cc"B"(x,x)` بصورت `cc"C"(x,x) ⇒ cc"D"(x,x)` است.
با فرض استقرا و قضیه .۲.۲۳.b:
`⊢x = y ⇒ (cc"C" (x, y) ⇒ cc"C" (x, x))`
و
`⊢ x = y ⇒ (cc"D"(x, x) ⇒ cc"D"(x, y))`.
از این رو، توسط توتولوژی:
`(A⇒(C_1⇒C))⇒[(A⇒(D⇒D_1))``⇒ (A⇒((C⇒D)⇒(C_1⇒D_1)))]`
داریم `⊢ x = y ⇒ (cc"B"(x, x) ⇒ cc"B" (x, y))`.
حالت ۳. `cc"B"(x,x)` بصورت `(∀z)cc"C"(x,x,z)` است.
با فرض استقرا، `⊢x=y⇒(cc"C"(x,x,z)⇒cc"C"(x,y,z))`.
`⊢x=y⇒(∀z)(cc"C"(x,x,z)⇒cc"C"(x,y,z))`.
با تمرین .۲.۲۷.a،
`⊢(∀z)(cc"C"(x,x,z)⇒cc"C"(x,y,z)))⇒``[(∀z)cc"C"(x,x,z)⇒(∀z)cc"C"(x,y,z)]`.
و بنابراین، توسط توتولوژی،
`(A⇒B)⇒((B⇒C)⇒(A⇒C))`
داریم: `⊢x=y⇒(B(x,x)⇒B(x,y))`.
■ ۲.۲۵ قضیه. (دو شرط برای حذف بنداشت (A۷))
(قضیه) فرض کنید K تئوری‌ای باشد که در آن (A۶) برقرار باشد و موارد زیر درست باشند.
a. طرحواره (A۷) برای همه فرمول‌های اتمی `cc"B"(x,x)` برقرار است، بقسمی که هیچ حرف تابعی یا ثابت انفرادی در `cc"B"(x,x)` روی نمی‌دهد و `cc"B"(x,y)` از `cc"B"(x,x)` با جایگزینی دقیقاً یک رویداد `x` با `y` بدست آمده است.
b. `⊢x=y⇒f_j^n(z_1, ... , z_n )=f_j^n(w_1, ... , w_n)` که در آن `f_j^n` حرف تابعی K است. `z_1, ... , z_n` متغیرها هستند و `f_j^n(w_1, ... , w_n)` دست آمده از `f_j^n(z_1, ... , z_n)` با جایگزینی دقیقا یک رویداد `x` با `y` است.
در این صورت، K یک تئوری با تساوی است.
اثبات:
با کاربرد پی‌درپی، فرض‌های ما را می‌توان به جایگزینی بیش از یک رویداد `x` توسط `y` گسترش داد، که هنوز قضیه ۲.۲۳ قابل دست آوردن باشد.
از طریق استفاده مکرر از مفروضات اولیه خود - که اجازه می‌دهد یک مورد تک متغیر `x` را با `y` در یک فرمول جایگزین کنیم - می‌توانیم این فرآیند را تعمیم دهیم رویدادهای چندگانه `x` را با `y` جایگزین کنیم. این جایگزینی گام به گام تضمین می‌کند که حتی زمانی که `x` چندین بار روی می‌دهد، هر جایگزینی تحت مفروضات اصلی معتبر باقی بماند.
بنا به قضیه ۲.۲۴، کافی است (A۷) را فقط برای فرمول‌های اتمی بدون ثابت‌های انفرادی ثابت کرد. اما، بنا بر فرض (a) می‌توانیم
`⊢(y_1=z_1∧...∧y_n=z_n)``⇒(B(y_1, ..., y_n)⇒B(z_1, ..., z_n))`
را برای همه متغیرهای `y_1, …, y_n, z_1, …, z_n` و هر فرمول اتمی `cc"B"(y_1, …, y_n)` بدون حروف تابعی یا ثابت‌های انفرادی بسادگی اثبات کنیم.
بنابراین، کافی است نشان دهیم:
(*) اگر `t(x,x)` یک جمله بدون ثابت‌های انفرادی باشد و `t(x,y)` از `t(x,x)` با جایگزین کردن برخی از رخدادهای `x` با `y` دست آمده باشد، آنگاه `⊢ x = y ⇒ t(x, x) = t(x, y)`.*
*- خواننده می‌تواند نحوه اعمال (*) را با استفاده از آن برای اثبات مورد زیر از (A۷) دریابد:
`⊢x=y⇒(A_1^1(f_1^1(x))⇒A_1^1(f_1^1(y)))`.
(*) را می‌توان با استفاده از فرض (b) با استقرا روی تعداد حروف تابعی در `t(x,x)` اثبات کرد و این را به عنوان تمرین رها می‌کنیم.
از قضیه ۲.۲۵ به راحتی می‌توان فهمید که وقتی زبان تئوری K فقط تعداد متناهی از حروف محمولی و تابعی دارد، فقط لازم است (A۷) برای فهرست متناهی از موارد خاص تأیید شود (در واقع، `n` فرمول برای هر `A_j^n` و `n` فرمول برای هر `f_j^n`).
■ تمرین (۲.۶۶ - ۲.۶۸)
۲.۶۶. تئوری تساوی مرتبه اول محض
فرض کنید `\text{K}_1` یک تئوری باشد که زبان آن فقط = را به عنوان حرف محمولی داشته باشد و هیچ حرف تابعی یا ثابت انفرادی در آن نباشد. نیز فرض کنید بنداشتهای سره آن از قرار زیر باشند:
`(∀x_1)x_1 = x_1`
`(∀x_1) (∀x_2) (x_1 = x_2 ⇒ x_2 = x_1)`
`(∀x_1)(∀x_2)(∀x_3)(x_1 = x_2 ⇒ (x_2 =x_3 ⇒ x_1 = x_3))`
نشان دهید که `\text{K}_1` یک تئوری با تساوی است.
راهنمایی: کافی است ثابت کنید:
`⊢ x_1 = x_3 ⇒ (x_1 = x_2 ⇒ x_3 = x_2)`
و
` ⊢ x_2 = x_3 ⇒ (x_1 = x_2 ⇒ x_1 = x_3)`.
به `\text{K}_1` تئوری تساوی مرتبه اول محض گفته می‌شود.
۲.۶۷. فرض کنید `\text{K}_2` یک تئوری باشد که زبان آن فقط = و < را به عنوان حروف محمولی داشته باشد و هیچ حرف تابعی یا ثابت انفرادی نداشته باشد. نیز فرض کنید `\text{K}_2` بنداشتهای سره زیر را داشته باشد.
a. `(∀x_۱)x_۱ = x_۱`
b. `(∀x_۱)(∀x_۲)(x_۱ = x_۲ ⇒ x_۲ = x_۱)`
c. `(∀x_۱)(∀x_۲)(∀x_۳)(x_۱ = x_۲ ⇒ (x_۲ = x_۳ ⇒ x_۱ = x_۳))`
d. `(∀x_۱)(∃x_۲)(∃x_۳)(x_۱ < x_۲ ∧ x_۳ < x_۱)`
e. `(∀x_۱)(∀x_۲)(∀x_۳)(x_۱ < x_۲ ∧ x_۲ < x_۳ ⇒ x_۱ < x_۳)`
f. `(∀x_۱)(∀x_۲)(x_۱ = x_۲ ⇒ ¬ x_۱ < x_۲)`
g. `(∀x_۱)(∀x_۲)(x_۱ < x_۲ ∨ x_۱ = x_۲ ∨ x_۲ < x_۱)`
h. `(∀x_۱)(∀x_۲)(x_۱ < x_۲ ⇒ (∃x_۳)(x_۱ < x_۳ ∧ x_۳ < x_۲))`
۲.۶۸. فرض کنید K هر تئوری با تساوی باشد. موارد زیر را ثابت کنید.
الف. `⊢ x_1 = y_1 ∧ … ∧ x_n = y_n ⇒`` t(x_1، …، x_n) = t(y_1، …، y_n)`.
که در آن `t(y_1,…, y_n)` از `t(x_1, …, x_n)` با جایگزینی `y_1, …, y_n` برای `x_1, …, x_n`، به ترتیب به دست آمده است.
ب. `⊢ x_1 = y_1 ∧ … ∧ x_n = y_n ⇒ (cc"B" (x_1, …, x_n) ⇔ cc"B" (y_1, …, y_n))`.
که در آن `cc"B" (y_1, …, y_n)` با جایگزین کردن `y_1, …, y_n` برای یک یا چند مورد از `x_1, …, x_n` به ترتیب، در فرمول `cc"B" (x_1, …, x_n)` بدست می‌آید. و `y_1, …, y_n` برای `x_1, …, x_n`، به ترتیب، در فرمول `cc"B" (x_1, …, x_n)` آزاد هستند.
حل ب:
مساله آشکارا به حالت جایگزینی یک تک متغیر در یک بار کاهش می‌یابد:
`⊢ x_1 = y_1 ⇒ t(x_1) = t(y_1)`.
از (A7)، `⊢ x_1 = y_1 ⇒ (t(x_1) = t(x_1) ⇒ t(x_1) = t(y_1))`.
از قضیه 2.23 (a)، `⊢ t(x_1) = t(x_1)`. بنابراین، `⊢ x_1 = y_1 ⇒ t(x_1) = t(y_1)`.
■ دو مثال: تئوری گروه‌ها و تئوری میدان‌ها
■ تئوری مقدماتی گروه‌ها (G)
در G حرف محمولی =، حرف تابعی `f_۱^۲` و ثابت انفرادی `a_۱` است. `f_۱^۲ (t ,s)` را با `t + s` و `a_۱` را با ۰ کوته نویسی می‌کنیم. بنداشتهای سره تئوری به قرار زیر هستند.
a. `x_۱ + (x_۲ + x_۳) = (x_۱ + x_۲) + x_۳`
b. `x_۱ + ۰ = x_۱`
c. `(∀x_۱)(∃x_۲)x_۱ + x_۲ = ۰`
d. `x_۱ = x_۱`
e. `x_۱ = x_۲ ⇒ x_۲ = x_۱`
f. `x_۱ = x_۲ ⇒ (x_۲ = x_۳ ⇒ x_۱ = x_۳)`
g. `x_۱ = x_۲ ⇒ (x_۱ + x_۳ =`` x_۲ + x_۳ ∧ x_۳ + x_۱ = ``x_۳ + x_۲)`
اینکه G یک تئوری با تساوی است به آسانی از قضیه ۲.۲۵ نتیجه می‌شود. اگر به بنداشتهای G فرمول زیر افزوده شود:
h. `x_۱ + x_۲ ⇒ x_۲ + x_۱`
به تئوری جدید تئوری مقدماتی گروه‌های آبلی گفته می‌شود.
■ تئوری مقدماتی میدان (F)
در `\text{F}` حرف محمولی =، حروف تابعی `f_۱^۲` و `f_۲^۲` و ثابت‌های انفرادی `a_۱` و `a_۲` هستند.
`f_۱^۲ (t ,s)` را با `t + s` و `f_۲^۲ (t ,s)` را با `t.s` و `a_۱` و `a_۲` را به ترتیب با ۰ و ۱ کوته نویسی می‌کنیم. بنداشتهای سره در F، افزون بر (a)–(h) در تئوری مقدماتی گروه‌ها در مثال قبل، به قرار زیر هستند:
i. `x_۱ = x_۲ ⇒ (x_۱ · x_۳ = x_۲ · x_۳ ∧ x_۳ · x_۱ = x_۳ · x_۲)`
j. `x_۱ · (x_۲ · x_۳) = (x_۱ · x_۲) · x_۳`
k. ` x_۱ · (x_۲ + x_۳) = (x_۱ · x_۲) + (x_۱ · x_۳)`
l. `x_۱ · x_۲ = x_۲ · x_۱`
m. `x_۱ · ۱ = x_۱`
n. `x_۱ ≠ ۰ ⇒ (∃x_۲)x_۱ · x_۲ = ۱`
o. `۰ ≠ ۱`
`\text{F}` یک تئوری با تساوی است. در این تئوری بنداشتهای (a)–(m) تئوری مقدماتی `R_C` حلقه‌های جابجایی با عنصر یکه [RC] را تعریف می‌کنند.
اگر حرف محمولی `A_۲^۲` را به `\text{F}` بیافزاییم، کوتاشده `A_۲^۲(t,s)` را `t < s` بگیریم و بنداشتهای (e) ، (f) و (g) تمرین ۲.۶۷ و همچنین
`x_۱<x_۲⇒x_۱+x_۳< x_۲+x_۳`
و
`x_۱ < x_۲ ∧ ۰ < x_۳ ⇒`` x_۱ · x_۳ < x_۲ · x_۳`،
را نیز به `\text{F}` بیافزویم، آنگاه تئوری جدید `\text{F}_<` را تئوری مقدماتی میدان‌های مرتب [R<] می‌نامند.
■ تمرین (۲.۶۹)
۲.۶۹.
الف. چه فرمول‌هایی باید دست آورده شود تا بتوان از قضیه ۲.۲۵ نتیجه گرفت که نظریه `\text{G}` در مثال ۱ یک تئوری با تساوی است؟
ب. نشان دهید که بنداشتهای (d)–(f) تساوی آمده در مثال ۱ را می‌توان با (d) و بنداشت `f'` در زیر جایگزین کرد.
`(f ′) : x_۱=x_۲⇒(x_۳=x_۲ ⇒ x_۱=x_۳)`
اغلب با تئوری‌های K مواجه می‌شویم که در آن = می‌تواند تعریف شود. یعنی یک فرمول `cc"E"(x, y)` با دو متغیر آزاد `x` و `y` وجود دارد، به قسمی که اگر `cc"E"(t, s)` را با `t = s ` کوته‌نویسی کنیم، بنداشتهای (A۶) و (A۷) در K قابل اثبات هستند. ما قرارداد می‌کنیم که اگر `t` و `s` ترم‌هایی باشند که به ترتیب برای `x` و `y` در `cc"E"(x,y)` آزاد نیستند، آنگاه با تغییر مناسب متغیرهای پابند (به تمرین ۲.۴۸ - تغییر متغیرهای پابند مراجعه کنید)، `cc"E"(x,y)` را با یک فرمول منطقاً هم‌ارز `cc"E"^***(x, y)` جایگزین می‌کنیم به قسمی که `t` و `s` برای `x` و `y`، به ترتیب، در `cc"E"^***(x,y)` آزاد باشند. در این صورت `t = s` کوتاه شده `cc"E"^***(t,s)` است. قضیه ۲.۲۳ و قضیه‌های مشابه ۲.۲۴ و ۲.۲۵ برای چنین تئوری‌هایی درست هستند. بسط اصطلاح نظریه با تساوی برای پوشش چنین تئوری‌هایی بدون مشکل است.
■ ■ ■ ■ ■
