نظریه برهان - منطق درآمدی یه منطق

نظریه برهان

استنتاج طبیعی - منطق گزاره‌ای (کلاسیک)

درآمد به منطق

روند نظریه برهان - منطق گزاره‌ای (کلاسیک)

≡

۱- سرآغاز

۲۴- تعمیم قاعده معرفی شرطی در NdPℓ

۲- نظریه برهان

۲۵- قضیه و استنتاج

۳- نظریه برهان / دستگاه استنتاج طبیعی NdPℓ

۲۶- قضیه برگردان (Importation)

۴- زبان صوری در NdPℓ

۲۷- قضیه سرریز (Principle of explosion)

۵- قواعد استنتاج صوری در NdPℓ

۲۸- نفی دوگانه

۶- طرح قواعد استنتاج آغازین در NdPℓ

۲۹- ترانهش (Transposition)

۷- استنتاج و برهان در NdPℓ

۳۰- قضیه تبدیل

۸- تعریف T ⊢ S

۳۱- قضیه دوگانگی

۹- برخی ویژگی‌های دستگاه NdPℓ

۳۲- تفکیک شرطی (⊃R)

۱۰- یکنوایی (Monotonicity)

۳۳- برهان خلف

۱۱- منطق نایکنوا (Non-monotonic logic)

۳۴- مجموعه‌های سازگار و ناسازگار فرمول‌ها

۱۲- استنتاج با مجموعه مقدمات نامتناهی

۳۵- نتیجه ناسازگاری

۱۳- ترایایی استنتاج (Transitivity)

۳۶- سازگاری و سازگاری مطلق

۱۴- استنتاج عضوی

۳۷- نتیجه ۱ سازگاری

۱۵- مقابله (Collation)

۳۸- دو نتیجه ناسازگاری

۱۶- قضیه در NdPℓ

۳۹- نتیجه مهم سازگاری

۱۷- قاعده دست-آوردنی (Derivable rule)

۴۰- بسته بودن استنتاجی

۱۸- نگاه کلی به قاعده 'معرفی شرطی ⊃I'

۴۱- تئوری صوری

۱۹- قضیه اینهمانی: α ⊃ α

۴۲- قضیه فشردگی

۲۰- قضیه واگردان / Exportation

۴۳- سازگاری بیشینه

۲۱- قیاس شرطی (Hypothetical Syllogism)

۴۴- تعبیر و فرامنطق در NdPℓ

۲۲- تعمیم ساده گردانی

۴۵- سازگاری دستگاه NdPℓ

۲۳- قضیه کاهش فصلی

■ سرآغاز

در یادداشت مقدمات نظریه برهان با مفاهیمی چون «استنتاج» و «برهان» آشنا شدیم. در قسمت «نگارش صورت در منطق» زبان صوری Pℓ را ساختیم و ویژگی‌های آن را با جزئیات بررسیی کردیم. در این قسمت، نظریه برهان در منطق گزاره‌ای را با موشکافی بیشتر مرور خواهیم کرد. در واقع در اینجا این نظریه را فقط با ۹ قاعده استنتاج ارائه می‌کنیم و خواهیم دید که دستگاه استنتاجی کپی (نیز در اینجا) در این دستگاه ۹ قاعده‌ای دست آمدنی است.

نظریه برهان - درآمد به منطق و رایانش
Bing AI. (2023) [نظریه برهان - Proof theory]. Personal communication.
دیوید هیلبرت و پرسش‌های بنیادین

در واقع، نظریه برهان در اوایل قرن بیستم توسط دیوید هیلبرت برای اثبات سازگاری روش‌های استدلالی مورد استفاده در ریاضیات، عمدتاً در نظریه مجموعه‌ها، نظریه اعداد و آنالیز ریاضی ایجاد شد.

■ نظریه برهان

نظریه برهان شاخه‌ای از منطق و رایانش است که بر سرشت خود برهان، ساختار آن و قواعد حاکم بر ایجاد برهان تمرکز دارد. این شامل زبان صوری، ساختارهایی که نمایانگر برهان هستند و جنبه‌های رایانش‌پذیری ساختن برهان است. همانطور که در  یادداشت مقدمات نظریه برهان دیدیم، نظریه برهان در ماهیت نحوی است، که این خلاف نظریه مدل است که ماهیت معنایی دارد. برخی از حوزه‌های نظریه برهان از جمله  اثبات قضیه بگونه خودکار / ماشینی (Automated theorem proving)، و نظریه پیچیدگی الگوریتم است.

گسترش یک نظریه برهان به دو روش انجام می‌پذیرد. این دو روش عبارت هستند از یکم دستگاه‌های صوری اصل موضوعی (Formal axiomatic systems). در یادداشت‌های آتی، منطق گزاره‌ها و محمولات (کلاسیک و برخی غیرکلاسیک) را با روش اصل موضوعی به تفصیل مرور خواهیم کرد.

روش دوم رده دستگاه‌های استنتاج طبیعی است. روش ارائه شده در فصل دهم [کتاب درآمد به منطق، قسمت ۷، دستگاه استنتاجی، حساب گزاره‌ها (با ۱۹ قاعده استنتاج)] گسترش یافته است از رده دستگاه‌های استنتاج طبیعی است.

رهیافت دستگاه استنتاج طبیعی در منطق توسط گرهارد گنتزن (Gerhard Gentzen ریاضیدان / منطق دان آلمانی، ۱۹۹۰ - ۱۹۴۵) ارائه گردیده است. در این رهیافت اصول موضوعه وجود ندارد و  قواعد استنتاج در آن "طبیعی" به نظر می‌آیند. آنچه در قسمت ۱ فصل ۲ کتاب دیدیم (نموداری کردن استدلال) و نیز قسمت ۴ فصل ۲ (قطعات استدلالی مرکب) شباهت به آنچه دارد که به نمایش برهان به شیوه گنتزنی موسوم است.

روشی که ما در این یادداشت پی‌خواهیم گرفت نیز از رده دستگاه‌های استنتاج طبیعی اما فقط با ۹ قاعده استنتاج خواهد بود.

■ نظریه برهان / دستگاه استنتاج طبیعی NdPℓ

یک دستگاه استنتاجی عبارت از دوتایی مرتب <L, R> است، که در آن، L یک زبان صوری و R مجموعه‌ای متناهی و ناتهی از قواعد استنتاج هستند. (R ممکن است دارای آنچه طرح‌های اصل موضوعی نامیده می‌شود نیز باشد).

در یک نظریه برهان (دستگاه منطقی)، قواعد استنتاج معیارهایی هستند بر آن‌که چه دنباله‌هایی‌ از جمله‌های خوش-ساخت زبان صوری در آن دستگاه یک استنتاج در آن دستگاه محسوب ‌شود. در ادامه یک دستگاه صوری خواهیم گستراند و جزئیات بیشتر را نیز شرح خواهیم‌ داد. ازآنجاکه دستگاه‌های صوری گونا‌گون وجود دارد، برای پرهیز از ابهام، دستگاه صوری معرفی‌شده در ادامه رNdPℓمی‌نامیم.

■ زبان صوری در NdPℓ

زبان صوری NdPℓ زبان صوری Pℓ است که در یادداشت «نگارش صورت و الگوریتم آن در منطق» معرفی شده است.

■ قواعد استنتاج صوری در NdPℓ

گیریم F مجموعه فرمول‌های Pℓ و Ƥ(F) مجموعه توانی F باشد. مراد از یک قاعده در NdPℓ که از این پس به آن قاعده استنتاج نیز خواهیم گفت، وجود یک رابطه بین Ƥ(F) و F است، به قسمی که در (این) رابطه بودن عضوی از Ƥ(F) با عضوی از F تصمیم‌پذیر باشد. بنابراین، اگر ri یک قاعده استنتاج، S یک زیرمجموعه‌ فرمول و α یک فرمول باشد، آنگاه:

S ri α

تصمیم پذیر ‌خواهد بود و در این صورت به α نتیجه مستقیم S و به S مقدمات↥ ri خواهیم گفت.

همان‌طور که گفته شد، مجموعه R، در دوگانه مرتب <L,R>، مجموعه‌ای متناهی از قواعد استنتاج است. برای دستگاه NdPℓ این مجموعه را، به شرحی که تعریف آن خواهد آمد، RPℓ می‌نامیم.

■ طرح قواعد استنتاج آغازین در NdPℓ

دستگاه NdPℓ دارای ۹ قاعده استنتاج، به‌عنوان قواعد استنتاج آغازین است. در جدول زیر این ۹ قاعده استنتاج همراه نام‌های نمادین آن‌ها آمده است.

این قواعد به دو گروه تقسیم‌شده‌اند،

۱- قواعد حذفی (Elimination Rules)،
۲- قواعد معرفی (Introduction Rules).

حرف E در نام نمادین یک قاعده مشخص حذفی بودن (Eliminative) این قاعده و حرف I نشان‌دهنده معرف بودن (Entroduction) آن است. علت انتخاب عبارت‌های حذفی و معرفی از شمای قاعده مشخص می‌شود. برای مثال، در قاعده ۱- (E⊃) رابط '⊃' حداقل در یک فرمول مقدمات به‌ عنوان رابط اصلی ظاهر شده که در نتیجه این قاعده وجود ندارد (حذف‌شده است)؛ و در قاعده ۳- (∧I) رابط '∧' به‌عنوان رابط اصلی در نتیجه این قاعده معرفی‌ شده است. تصمیم‌پذیری آن‌ها، با توجه به آنچه در بحث خوانش یکتای فرمول گفته شد هرآینه آشکار است.

طرح ۹ قاعده قاعده استنتاج در دستگاه NdPℓ=<LP ,RPℓ>
RPℓ={r۱, r۲, {r۳, r۴}, {r۵, r۶}, r۷, r۸, r۹, r۱۰, r۱۱}

قواعد حذفی

۱:{α ⊃ β, α} r۱ β حذف شرطی⊃E
۲:

{α ∧ β} r۲.۱ α
{α ∧ β} r۲.۲ β

حذف عطفی∧E
۳:{α ∨ β, α ⊃ δ, β ⊃ δ} r۳ δحذف فصلی∨E
۴:{~α} r۴ α ⊃ βحذف نقیض~E
۵:{‍‍‍~‍‍‍~α} r۵ αحذف نقض دو‌گانه~~E

قواعد معرفی

۶:(α ⊢ β) ⇒ ⊢ ( α ⊃ β) r۶ [C.P.]معرفی شرطی⊃I
۷:{α, β} r۷ α ∧ βمعرفی عطفی∧I
۸:

{α } r۸.۱ α ∨ β
{β} r۸.۲ α ∨ β

معرفی فصلی∨I
۹:{α ⊃ β, α ⊃ ~β} r۹ ~αمعرفی نقیض~I
در جدول زیر  ۹ قاعده استنتاج در NdPℓ به‌صورت نموداری آمده است. همان‌طور که می‌توان دید، برای قاعده '~~E' قاعده معرفی نقض دوگانه وجود ندارد. در ادامه قاعده معرفی نقض دوگانه را بر پایه این ۹ قاعده مبنایی (به عنوان قاعده دست آوردنی / Derived rule) به دست خواهیم آورد.

حذف شرطی

α ⊃ β α
—————(⊃E)-r۱
β

معرفی شرطی

α
.
.

β
————(⊃i)-r۶[C.P.]
α ⊃ β

حذف عطفی -۱

α ∧ β
————(∧E۱)-r۲.۱
α

معرفی عطفی

α β
———(∧I)-r۷
α ∧ β

حذف عطفی -۲

α ∧ β
————(∧E۲)-r۲.۲
β

معرفی فصلی -۱

α
———(∨I۱)-r۸.۱
α ∨ β

حذف فصلی

α∨β α⊃δ β⊃δ
————————(∨E)-r۳
δ

معرفی فصلی -۲

β
———(∨I۲)-r۸.۲
α ∨ β

حذف نقیض

~α
———(~E)-r۴
α ⊃ β

معرفی نقیض

α⊃β α⊃~β
———————(~I)-r۹
~α

حذف نقض دو‌گانه

~~α
———(~~E)-r۵۰
α

■ استنتاج و برهان در NdPℓ

گیریم S یک مجموعه فرمول و β یک فرمولِ NdPℓ باشند. ‌گوییم:

β یک استنتاج از S [یا β یک نتیجه صوری S یا فقط نتیجه S] در NdPℓ است اگر و تنها اگر دنباله فرمول:

α۱, α۲, . . . ,αn-۱, αn :(ب)

وجود داشته باشد، به قسمی که:

۱.

هر عنصر (ب) عضو S یا یک نتیجه مستقیم عناصر قبل خود در (ب) [یا هر دو] باشد؛

و

۲.

αn همان β باشد.

☚: اگر β نتیجه S باشد، همچنین گفته می‌شود β از S درNdPℓ قابل استنتاج است یا β از S در NdPℓ دست-آوردنی است .

• برهان صوری / Formal proof:

به دنباله (ب) در بالا برهان صوری [همچنین، برهان نحوی / Syntactical proof] در NdPℓ می‌گوییم.

☚: به ‌طور معمول در دستگاه‌های صوری نماد '⊢' برای نمایاندن: β نتیجه صوری S است؛ یا: S به‌ طور صوری β را نتیجه می‌دهد، به کار می‌رود. بنابراین، اگر در دستگاه β - NdPℓ یک نتیجه صوری S باشد، آنگاه می‌نویسیم:

S ⊢NdPℓ β

و آن را یک استنتاج صوری یا فقط یک استنتاج در NdPℓ می‌‌نامیم. به هر عضو S یک مقدمه، به S مقدمات و به β نتیجه استنتاج صوری میگوییم. نماد NdPℓ سمت راست '⊢' تأکید به این نکته مهم است که این یک استنتاج صوری در دستگاه NdPℓ است. اگر نشان داده شود دنباله (ب) و جود ندارد آنگاه می‌نویسیم:

S ⊬NdPℓ β

و می‌گوییم β از S در NdPℓ قابل استنتاج (دست آوردنی) نیست.

☚ ازآنجاکه موردنظر در اینجا صرفاً دستگاه NdPℓ است ازاین‌پس از آوردن نام دستگاه در S⊢β، مگر برای تأکید، خودداری می‌کنیم.

• برهان صوری (مثال)

• مثال (۱)- فرض کنید:

S = {(α ∨ β) ⊃ (λ ∧ γ), α ∨ β}.

نشان دهید:

. S ⊢ λ

می‌گوییم دنباله:

u =< (α ∨ β) ⊃ (λ ∧ γ), α ∨ β, λ ∧ γ, λ >

برهان S ⊢ λ است؛ زیرا، آخرین عنصر u، یعنی λ، نتیجه استنتاج و هر عنصر u عضوی از S یا نتیجه مستقیم عناصر قبل خود در uاست. یکی از روش‌های نمایاندن برهان بودن دنباله u به گونه زیر است، که با آن در فصل‌های ۹ و ۱۰ کتاب آشنا شده‌ایم.

ترتیبعناصر دنباله u موجه سازی
۱.(α ∨ β) ⊃ (λ ∧ γ) مقدمه(عضو S)
۲.α ∨ βمقدمه(عضو S)
۳.λ ∧ γ۱ و ۲ و ⊃E
۴.λ۳ و ∧E۱

روش دیگر نمایاندن این برهان نموداری سازی آن مطابق زیر است[فصل ۲ کتاب " نمودار سازی استدلال" را ببینید]:

proofdg1w.png

☚ یادآور:

۱- در S ⊢ β اگر اعضای S را بتوان فهرست کرد آنگاه بجای S فقط اعضای آن را می‌نویسند.

برای مثال اگر S={(α ∨ β) ⊃ (λ ∧ γ), α ∨ β} و داشته باشیم S⊢β به‌جای S می‌نویسند:

(α ∨ β) ⊃ (λ ∧ γ), α ∨ β ⊢β.

۲- رسم است بجای S∪{α} ⊢β بنویسند:S, α ⊢β .

• مثال (۲)- نشان دهید (α ⊃ β), α ⊢ (α ∧ β).

برهان:

۱. α ⊃ βمقدمه
۲.αمقدمه
۳.β۲، ۱، ⊃E
۴.α ∧ β۲، ۳، ∧I

■ تعریف T ⊢S

فرض کنید S و T دو مجموعه فرمول باشند، به‌گونه‌ای که هر عضو S نتیجه T باشد. در این‌ صورت نوشته:

T ⊢ S

و می‌گوییم S نتیجه T است.

برای مثال، فرض کنید:

T={(α∨β)⊃(λ∧γ), α∨β, (α⊃β), α} و S = {λ , α∧β}

با توجه به مثال ۱ و ۲ در بالا می‌توان نوشت: T⊢S و گفت S یک نتیجه صوری T است.

■ برخی ویژگی‌های دستگاه NdPℓ

فرض کنید δ ،β ،α فرمول، S و T دو مجموعه فرمول باشند، آنگاه ویژگی‌های زیر برای دستگاه صوری (آن‌گونه که اینجا تعریف شد) برقرار است.

■ ۱. یکنوایی (Monotonicity)

<*پیش از خواندن این بند، مرور بحث اعتبار در استدلال استنتاجی در کتاب (در اینجا) مفید است.*>

اگر δ نتیجه صوری S و S زیرمجموعه T باشد، آنگاه δ نیز نتیجه صوری T است. به عبارت دیگر:

S ⊢ δ, S ⊂ T ⇒ T ⊢ δ.

منطق یکنوا (یکنواخت)

اثبات این گزاره آسان است و درواقع نتیجه مستقیم تعریف برهان در NdPℓ است. میگوییم؛ طبق فرض داریم:

S ⊢ δ.

بنابراین، برهان:

≺α۱, α۲, . . . ,αn-۱, αn ≻

(که در آنαn  همان δ است) وجود دارد. این دنباله نیز برهان T⊢δ است. زیرا هر عنصر آن عضو T است [بنا به فرض، S⊂T] یا یک نتیجه مستقیم عناصر قبل خود است [بنا به فرض، S ⊢δ].

به‌عبارت‌دیگر:

اگر δ نتیجه مقدمات S باشد، آنگاه δ نتیجه S با هر تعداد مقدمه دلخواه افزوده به S نیز هست.

این خاصیت به یکنوایی (Monotonicity) موسوم است و به هر دستگاه منطقی با این خاصیت منطق یکنوا گفته می‌شود. برای مثال، اگر داشته باشیم:

α ⊢ β

و Δ یک مجموعه فرمول دلخواه باشد، آنگاه نیز داریم:

Δ, α ⊢ β.

■ منطق نایکنوا (Non-monotonic logic)

به منطقی که در آن رابطه زیر برقرار باشد منطق نا یکنوا گفته می‌شود:

S ⊢ p ⇔ p ∈ S

■ ۲. استنتاج با مجموعه مقدمات نامتناهی

<*پیش از خواندن این بند، مرور بحث اعتبار در استدلال استنتاجی در کتاب (در اینجا) مفید است.*>

این ویژگی را به صورت زیر بیان می‌کنیم (توجه داریم T یک مجموعه فرمول دلخواه است که می‌تواند نامتناهی هم باشد):

T ⊢ β اگر و تنها اگر زیرمجموعه متناهی S از T وجود داشته باشد، به قسمی که S⊢β .

این خاصیت دو شرطی است، بنابراین ثابت می‌کنیم:

(۱)- اگر T نامتناهی و S یک زیرمجموعه متناهی آن باشد به قسمی که S ⊢ β ، آنگاه T⊢β ؛

(۲)- گر T نامتناهی و T⊢β، آنگاه زیرمجموعه متناهی S از T وجود دارد به قسمی که S⊢β .

اثبات:

بند (۱) نتیجه مستقیم یکنوایی است.

برای اثبات بند (۲) ‌می‌گوییم ازآنجاکه T⊢β، پس بنا به تعریف استنتاج صوری، دنباله‌ای متناهی از عناصر T به‌عنوان برهان وجود دارد. عناصر این دنباله همان عناصر مجموعه S خواهند بود. اکنون می‌توان گفت، یک دنباله نامتناهی نیز می‌تواند یک برهان باشد.

■ ۳. ترایایی استنتاج (Transitivity)

فرض کنید γ فرمول باشد، آنگاه:

T ⊢ S, S ⊢γ ⇒ T ⊢ γ

به‌ویژه اگر S فقط عضو β را داشته باشد آنگاه:

T ⊢ β, β ⊢γ ⇒ T ⊢ γ

همچنین اگر T فقط عضو α را داشته باشد آنگاه:

α ⊢ β, β ⊢γ ⇒ α ⊢ γ

این خاصیت نتیجه ویژگی دوم است.

■ ۴. استنتاج عضوی

بنا به ویژگی استنتاج عضوی:

اعضای یک مجموعه فرمول نتیجه‌های صوری آن مجموعه هستند.

اثبات:

گیریم S مجموعه فرمول و α∈S. دنباله تک عضوی <α۱=α> را در نظر بگیرید. این دنباله یک برهان S⊢α است، زیرا تعریف برهان در NdPℓ را برمی‌آورد (آخرین عضو آن نتیجه و متعلق به مجموعه مقدمات نیز است.)

اینهمانی (α ⊢ α)

بنا بر استنتاج عضوی وقتی S={α} داریم: {α}⊢α، که این یعنی: α⊢α.

■ ۵. مقابله (Collation)

بنا بر ویژگی مقابله داریم:

S ⊢ α ⊃ β ⇒ S, α ⊢ β

اثبات:

فرضS ⊢ α ⊃ β۱.
۱ و یکنواییS, α ⊢ α ⊃ β۲.
عضویتS, α ⊢ α۳.
از ۳، ۲ و ⊃E S, α ⊢ β۴.

☚ این ویژگی برای هر دستگاه صوری که قاعده ⊃E در آن هست برقرار است.

■ قضیه در NdPℓ

گوییم فرمول α یک قضیه NdPℓ ‌است (α در NdPℓ اثبات شدنی است)، اگر و تنها اگر α از مجموعه مقدمات تهی دست-‌آمدنی باشد.

به‌عبارت‌دیگر:

α قضیه NdPℓ است. {}⊢α ⇔

☚ معمولاً به‌جای {}⊢α ⇔ به نوشتن ⊢α ⇔ بسنده می‌گردد.

☚ یک قضیه، آن‌طور که تعریف شد، درواقع یک شمای قضیه‌ای است و معرف تعداد نامتناهی مورد قضیه‌ای است. برای مثال، گیریم α⊃(β⊃α) یک قضیه در NdPℓ باشد. در این صورت:

p⊃(q⊃p) و (q⊃p)⊃(r ⊃ (q⊃p))

نمونه‌هایی از قضیه در NdPℓ خواهند بود.

☚ اگر فرمولی قضیه باشد، بنا بر یکنوایی و ترایایی می‌توان این فرمول را به‌عنوان یک خط در برهان (یک عنصر در دنباله برهان) معرفی کرد. در ادامه و پس از معرفی قاعده معرفی شرطی نمونه‌های بسیار از قضیه و برهان آن خواهیم دید.

☚ در متون فارسی منطق ارسطویی مراد از "قضیه" گفتاری است که ازجمله ممکن است درست یا نادرست باشد. در منطق جدید قضیه / (Theorem) صرفاً یک صورت (فرمول خوش-ساخت) در یک دستگاه استنتاجی مشخص است که در آن دستگاه دارای برهان صوری است.

• ترایایی قضیه:

گیریم α قضیه NdPℓ باشد و داشته باشیم α⊢β، آنگاه β نیز قضیه NdPℓ است. این نتیجه تعریف قضیه و ویژگی ترایایی '⊢' است.

■ قاعده دست-آوردنی (Derivable rule)

یک قاعده دست-آوردنی (Derivable rule) در NdPℓ (یا هر دستگاه استنتاجی) یک قاعده استنتاج است که نتیجه مستقیم آن از مقدمات آن دست آوردنی باشد. این قواعد را می‌توان همچون قواعد استنتاج آغازین در روند برهان به کار زد. در ادامه چندین قاعده ازاین‌گونه، مانند قیاس شرطی، عکس نقیض، قیاس اقترانی و مانند آن‌ها، را به دست خواهیم آورد.

■ نگاه کلی به قاعده 'معرفی شرطی ⊃I'

کار زدن قاعده معرفی شرطی [برهان شرطی را ببینید] در زبان طبیعی بدیهی می‌نماید، آن‌قدر که می‌تواند دیده نشود. فرض کنید می‌خواهیم قضیه هندسی "اگر در مثلث [دلخواه] ABC دو زاویه برابر باشند، آنگاه در مثلث ABC دو ضلع برابرند" را ثایت کنیم. این قضیه به صورت یک گزاره شرطی [استلزام مادی] بیان شده است. مقدم این شرطی، یعنی گزاره "در مثلث [دلخواه] ABC دو زاویه برابرند" را p و تالی آن، یعنی گزاره "در مثلث ABC دو ضلع برابرند" را q می‌‌نامیم. در عمل مسئله را مطابق زیر صورت‌بندی و حل می‌کنیم:

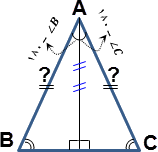مثلث با دو زاویه مساوی
۱. p: در مثلث [دلخواه] ABC دو زاویه برابر است. فرض ۱
۲.. . . . . . . . . . . . . . . . . . . . . . . . . . .. . . .
.. . . . . . . . . . . . . . . . . . . . . . . . . . .. . . .
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
n.q: در مثلث ABC دو ضلع برابر است. . . . .
n+۱ p⊃qاگر در مثلث [دلخواه] ABC دو زاویه برابر باشند آنگاه در مثلث ABC دو ضلع برابر است. ۱ تا n و قاعده معرفی شرطی

در خط ۱ گزاره p، یعنی "در مثلث ABC دو زاویه برابر است" را فرض گرفته‌ایم و این فرض فارغ از درستی یا نادرستی آن است (و فارغ از اینکه آیا مثلثی با دو زاویه مساوی وجود دارد؟) سپس با گام‌های منطقی، با استناد به فرض گرفته شده و قضایای پیشین هندسه گزاره q، یعنی "در مثلث ABC دو ضلع برابر است" را در خطnام به دست آورده‌ایم. سپس در خط n+۱ قضیه مورد اثبات، مدعای اصلی، به‌عنوان نتیجه برهان ظاهر شده است. اما این خط بنا بر چه قاعده‌ای به دست آمده است؟ جواب بنا بر روند پیدایش خط‌های ۱ تا n و قاعده معرفی شرطی است. اکنون دیگر p⊃q در هندسه اقلیدسی فقط یک استلزام مادی نیست بلکه یک قضیه نیز است.

⦁ قاعده استنتاج 'معرفی شرطی'

گیریم α ⊢ β ، آنگاه خواهیم داشت: ⊢α ⊃ β. به عبارت دیگر داریم:

α ⊢ β ⇒ ⊢ (α ⊃ β).

با توجه به تعریف رابطه ' ⊢' می‌توان α⊢β را با دنباله برهانی:

<α, . . .,β>

بیان کرد و ازاینجا طرح قاعده استنتاج معرفی شرطی را به‌صورت زیر نیز نشان داد.






(⊃I)		α
.
.
.
.
β
α ⊃ β

■ قضیه اینهمانی: α ⊃ α

بنا بر اینهمانی داریم α⊢α. بنا بر قاعده معرفی شرطی می‌نویسیم:

α ⊢ α ⇒ ⊢ α ⊃ α

بنابراین،  α⊃α یک قضیه NdPℓ است.

■ قضیه واگردان / Exportation

برهان این قضیه (واگردان / Exportation) را به شیوه‌ای که در کتاب (درآمد به منطق: برهان شرطی) شرح داده شده است می‌آوریم. [برهانِ نیمه ۲ در ادامه، ب.۱.۷، خوهد آمد.]

۱- ⊢((α ∧ β) ⊃ γ) ⊃ (α ⊃ (β ⊃ γ)) ↥
۲- ⊢(α ⊃ (β ⊃ γ)) ⊃ ((α ∧ β) ⊃ γ) ↥

برهان:

۱.(α∧ β ) ⊃ γفرض ۱
۲.αفرض ۲
۳.βفرض ۳
۴.α∧ β۲، ۳، ∧I
۵.γ۱، ۴، ⊃I
۶.β⊃ γ۳-۵، (⊃I)
۷. α⊃ (β ⊃ γ))۲-۶، (⊃I)
۸.((α ∧ β) ⊃ γ) ⊃ (α ⊃ (β ⊃ γ)) ۱-۷، (⊃I)

در زیر برهان بالا به‌ صورت نموداری نمایش داده ‌شده است.

[α]۲فرض [β]۳فرض
—————————————(∧I)
α ∧ β [(α ∧ β) ⊃ γ]۱فرض
——————————————(⊃E)
γ
———— (تخلیه فرض ۳)
β ⊃ γ
————————(تخلیه فرض ۲)
(α ⊃ (β ⊃ γ))
——————————————(تخلیه فرض ۱)
((α ∧ β) ⊃ γ) ⊃ (α ⊃ (β ⊃ γ))

■ قیاس شرطی (Hypothetical Syllogism)

α ⊃ β ∧ β ⊃ γ ⊢ α ⊃ γ

در زیر برهان به ‌صورت نموداری نمایش داده‌ شده است.

α ⊃ βمقدمه [α]فرض
———————————(⊃E)
β ⊃ γمقدمه β
————————(⊃E)
γ
—————(تخلیه فرض)
α ⊃ γ

■ شرکت‌پذیری و جابه‌جایی رابط '∧':

⊢(α ∧ β) ∧ γ ≡ α ∧ (β ∧ γ)
⊢α ∧ β ≡ β ∧ α

اثبات ☚↧

خاصیت شرکت پذیری:

(۲) ⊢α∧(β∧γ)⊃(α∧β)∧γ(۱) ⊢(α∧β)∧γ⊃α∧(β∧γ)
فرضα∧(β∧γ) ۱.
۱، ∧Eβ∧γ۲.
۲، ∧Eγ۳.
۲، ∧Eβ۴.
۱، ∧Eα۵.
۴، ۳ ∧Iβ∧γ۶.
۵، ۶، ∧Iα∧(β∧γ)۷.
۱-۷، ⊃Iα∧(β∧γ)⊃(α∧β)∧γ(۸.
فرض(α∧β)∧γ ۱.
۱، ∧Eα∧β۲.
۲، ∧Eα۳.
۲، ∧Eβ۴.
۱، ∧Eγ۵.
۴، ۵، ∧Iβ∧γ۶.
۳، ۶، ∧Iα∧(β∧γ)۷.
۱-۷، ⊃Iα∧β)∧γ⊃α∧(β∧γ) (۸.

اکنون با توجه به (۱) و (۲) و نیز سطح اولویت رابط‌ها می‌توان نوشت:

α∧β∧γ⊣⊢
⊣⊢(α∧β)∧γ⊃α∧(β∧γ)⊣⊢
⊣⊢α∧(β∧γ)⊃(α∧β)∧γ)

و مثل آن را برای α۱∧α۲ ∧…∧αn نیز نوشت. به همین روش می‌توان خاصیت جا‌به‌جایی رابط '∧' را نیز نشان داد.

■ شمای زبرین (⊤) و شمای زیرین (⊥)

با توجه به ویژگی جابجایی '∧' و '∨' و نیز تعریف '⏉' و '⏊' می‌توان نوشت:

⏉ ⊢ ⊣ ~χ ∨ χ,
⏊ ⊢ ⊣ ~χ ∧ χ

■ تعمیم (∧I):

 {α۱, α۲, . . . ,αn} ⊢ α۱∧ α۲ ∧ . . . ∧ αn

این تعمیم با استفاده از روش استقرا به‌آسانی ‌اثبات می‌شود.

■ قضیه ساده گردان

⊢ α ∧ β ⊃ α
⊢ α ∧ β ⊃ β

اثبات:

فرض∧ β α۱.
۱، ∧Eβ۲.
۱-۲، ⊃I∧ β ⊃ βα۳.
فرض∧ β α۱.
۱، ∧Eα۲.
۱-۲، ⊃I∧ β ⊃ αα۳

■ تعمیم ساده گردانی:

(آ): ⊢ (α۱ ∧ α۲ ∧ . . . ∧ αn) ⊃ αi; ۲ ≤ i ≤n

اثبات:

ابتدا نشان می‌دهیم:

α ∧ β ⊢ α ∧ β ∧ β و α ∧ β ∧ β ⊢ α ∧ β

⊢ α∧β∧β ⊃ α∧β(a۲):⊢ α∧β ⊃ α∧β∧β(a۱):
فرضα∧β∧β ۱.
۱، ∧Eα∧β۲.
۱-۲، ⊃Iα∧β∧β ⊃ α∧β ۳.
فرضα∧β۱.
۱، ∧Eβ۲.
۱، ۲، ∧Iα∧β∧β ۳.
۱-۳، ⊃Iα∧β ⊃ α∧β∧β ۴.

برای اثبات (آ) از روش استقرا روی اندیس‌ها استفاده می‌کنیم. برای n=۲ بنا به قضایای ساده گردانی نتیجه حاصل است. یعنی:

⊢(α۱ ∧ α۲) ⊃ α۱ و ⊢(α۱ ∧ α۲) ⊃ α۲.

فرض می‌کنیم برای عدد ۲≤m و برای هر j به قسمی که j≤m داریم (فرض استقرا):

⊢( α۱ ∧α۲ ∧ . . . ∧ αm) ⊃ αj

باید نشان داد برای هر j به قسمی که j≤ m+۱ داریم:

⊢(α۱ ∧ α۲ ∧ . . . ∧ αm ∧ αm+۱) ⊃ αj .

۱- داریم:

α۱ ∧ α۲ ∧ . . . ∧ αm ∧ αm+۱⟺
⟺ (α۱ ∧ α۲ ∧ . . . ∧ αm) ∧ αm+۱ ⟺
⟺ (α۱ ∧ α۲ ∧ . . . ∧ αm ∧ αm+۱) ∧ αm+۱

۲- از ۱ و (a۲) داریم:

⊢(α۱∧α۲ ∧ . . . ∧αm∧αm+۱)⊃αm+۱;

۳- از ۱ و (a۱) داریم:

⊢(α۱∧α۲ ∧ . . . ∧αm∧αm+۱)⊃(α۱∧α۲ ∧ . . . ∧αm);

اکنون می‌گوییم j مساوی m+۱ یا کوچک‌تر مساوی m است.

۴- اگر j=m+۱ باشد، از خط ۲ داریم:

⊢(α۱∧α۲ ∧ . . . ∧αm∧αm+۱)⊃αj که نتیجه حاصل است.

۵- اگر j≤ m باشد، بنا به فرض استقرا داریم:

⊢(α۱∧α۲ ∧ . . . ∧αm)⊃αj.

و نیز از خط ۳، خط ۵ و قیاس شرطی داریم:

(α۱∧α۲ ∧ . . . ∧αm∧αm+۱)⊃αj.

و از این نتیجه حاصل و اثبات تمام است.

■ قضیه کاهش فصلی

⊢( α ∨ α) ⊃ α

اثبات:

[α∨α]فرض α⊃αقضیه α⊃αقضیه
————————————————(∨E)
α
——————(تخلیه فرض)
(α∨α)⊃α

■ تعمیم قاعده معرفی شرطی در NdPℓ

(I.C.G): S, α ⊢ β ⇔ S ⊢ (α ⊃ β)

آنچه را در اینجا تعمیم معرفی شرطی (I.C.G) نامیده در دستگاه‌های اصل موضوعی به فراقضیه استنتاج شناخته می‌شود. توضیح بیشتر در اینجا این که (همانطور که در یادداشت‌های بعد خواهیم دید)، قاعده ⊃I در دستگاه‌های اصل موضوعی به‌عنوان یک قاعده استنتاج پایه حضور ندارد. در دستگاه‌های اصل موضوعی قاعده ⊃I حالت خاص فرا-قضیه‌ استنتاج، وقتی S در (I.C.G) تهی باشد، است.

اثبات:

اثبات رابطه (I.C.G) از راست به چپ بالاتر تحت عنوان "مقابله" آمده است. اثبات آن در جهت دیگر به‌قرار زیر است:

اگر S=∅ آنگاه  I.C.G قاعده ⊃I است، پس فرض می‌کنیم:

S = {α۱, α۲, . . . ,αn}.

بنابراین، باید نشان داد:

α۱, α۲, . . . ,αn, β ⊢ γ ⇒ α۱, α۲, . . . ,αn⊢ (β⊃γ)

مقدمه{α۱, α۲, . . . ,αn, β} ⊢ γ۱.
تعمیم ساده گردان،
تعریف T⊢S و ترایایی		(α۱∧α۲∧ . . . ∧αn∧β) ⊢ {α۱, α۲, . . . ,αn, β}۲.
از ۲، ۱ و ترایایی(α۱∧α۲∧ . . . ∧αn ∧ β) ⊢ γ۳.
از ۳ و شرکت پذیری⊢ (α۱∧α۲∧ . . . ∧αn) ∧ β ⊃ γ۴.
از ۴ و واگردان⊢ (α۱∧α۲∧ . . . ∧αn) ⊃ (β⊃γ)۵.
از ۵ و مقابله(α۱∧α۲∧ . . . ∧αn) ⊢ β⊃γ۶.
از تعمیم ∧Iα۱, α۲, . . . ,αn ⊢ (α۱∧α۲∧ . . . ∧αn)۷.
از ۷، ۶ و ترایاییα۱, α۲, . . . ,αn ⊢ (β⊃γ)۸.

■ قضیه و استنتاج

با توجه به تعمیم قاعده شرطی در بالا می‌توان گفت:

در NdPℓ: برای هر استنتاج یک قضیه نظیر وجود دارد و برای هر قضیه یک استنتاج نظیر وجود دارد.

■ مثال برای کار زدن تعمیم قاعده معرفی شرطی:

نشان می‌دهیم:

(α ⊃ β) ⊢ (α⊃(α ∧ β))

اثبات:

داریم:

آ(α⊃β), α ⊢ (α ∧ β)
⊃I.C.G
⇒
(α⊃β) ⊢ α⊃(α∧ β)

بنابراین:

۱. α ⊃ βمقدمه
۲.αفرض
۳.β۲، ۱، ⊃E
۴.α ∧ β۲، ۳، ∧I
۵.(α ⊃ β), α ⊢ (α ∧ β)) ۱، ۲ - ۴
۶.(α ⊃ β) ⊢ (α ⊃ (α ∧ β))۵ و ⊃I.C.G

در برهان بالا، خط ۵ از خط‌های قبل و خط ۶ از خط ۵ و آ به‌دست ‌آمده‌اند.

■ قضیه برگردان (Importation)

⊢(α ⊃(β ⊃ γ)) ⊃ ((α ∧ β) ⊃ γ)

☚ این قضیه را که وارون قضیه واگردان است قضیه برگردان می‌نامیم. بنابراین، می‌توان نوشت:

(α ⊃(β ⊃ γ)) ⊢ ((α ∧ β) ⊃ γ)
((α ∧ β) ⊃ γ) ⊢ (α ⊃(β ⊃ γ))

برهان:

فرض ۱ α ⊃ (β ⊃ γ)۱.
فرض ۲ α ∧ β۲.
۲، ∧Eα۳.
۳، ۱، ⊃Eβ ⊃ γ۴.
۲، ∧Eβ۵.
۵، ۴، ⊃Eγ۶.
۱، ۲ - ۶α ⊃(β ⊃ γ), (α ∧ β) ⊢ γ۷.
۷ و ۲بار کارزدن IG⊂⊢(α ⊃(β ⊃ γ))⊃((α ∧ β) ⊃ γ)۸.

■ قضیه سرریز (Principle of explosion)

⊢α⊃ (~α ⊃ γ)

برهان:

فرض ۱α۱.
فرض ۲~α۲.
۲، ~Eα ⊃ γ ۳.
۱، ۳، ⊃Eγ ۴.
۱ - ۴α, ~α ⊢ γ۵.
۵ و دو۲بار کارزدن IG⊂ ⊢ α⊃(~α ⊃ γ) ۶.

نتیجه:

بنا به قضیه برگردان داریم:

(آ): ⊢(α ∧ ~α) ⊃ γ

از (آ) در سطر قبل و ویژگی مقابله خواهیم داشت:

(ب): α ∧ ~α ⊢ γ

(ب) در سطر قبل را به‌ عنوان یک قاعده دستآوردی به صورت زیر می‌نوسیم:

χ ~χ
—————⊥E
γ

☚:

قاعده حذف نقیض (~E) از قاعده ⊥E در بالا و کارزدن (⊃I) قابل دستآورد است. بنابراین، می‌توان ⊥E را به‌جای قاعده حذف نقیض در جدول قواعد معرفی کرد. در این صورت قاعده حذف نقیض یک قاعده استنتاج آغازین نخواهد بود، بلکه یک قاعده دستآوردی خواهد بود.

■ نفی دوگانه

⊢ ~~α ⊃ α

برهان:

فرض~~α۱.
۱، ~~Eα۲.
۱ تا ۲ ~~α ⊢ α ۳.
۳ و ⊃I ⊢ ~~α ⊃ α ۴.

وارون این قضیه (⊢α⊃~~α) را در دادمه ببینید.

■ لم E۱:

(E۱): ⊢ α ⊃ (β ⊃ α)

برهان:

واگردان ((α ∧ β)⊃α ) ⊃ (α ⊃(β ⊃ α)) ۱.
ساده گردان(α ∧ β) ⊃ α۲.
۱، ۲ و (⊃I)α ⊃(β ⊃ α)۳.

■ لم E۲:

(E۲): ⊢ (~α ⊃ ~β) ⊃ ((~α ⊃ β) ⊃ α)

برهان:

فرض ~α⊃~β۱.
فرض~α⊃β۲.
۲، ۱، ~I~~α۳.
نقض دوگانه~~α⊃α ۴.
۳، ۴، ⊃Eα۵.
۱ تا ۵ (~α⊃~β), (~α⊃β)⊢α ۶.
۶ و دو بار کار زدن IG⊂ ⊢(~α⊃~β) ⊃ ((~α⊃β)⊃α) ۷.

■ ترانهش↝ (Transposition)

⊢(~α ⊃ ~β) ⊢ ⊣ (β ⊃ α)

برهان:

۱- برهان:⊢(~α ⊃ ~β) ⊃ (β⊃α)آ
فرض ~α ⊃ ~β۱.
(۲e)(~α⊃~β) ⊃ ((~α⊃β)⊃α) ۲.
(e۱)β ⊃ (~α ⊃ β) ۳.
۱، ۲، ⊃E(~α⊃β) ⊃ α۴.
۳، ۴، قیاس شرطی β ⊃ α۵.
از ۱ تا ۵(~α ⊃ ~β) ⊢ (β ⊃ α)۶.
۶ و IG⊂ ⊢(~α ⊃ ~β) ⊃ (β ⊃ α)۷.
۲- برهان: ⊢(α⊃β) ⊃ (~β⊃~α)
ابتدا نشان می‌دهیم:⊢(α⊃β) ⊃ (~~α⊃~~β) ب
۱.
فرضα⊃β۱.
~~α ⊃ α۲.
۲، ۱، قیاس شرطی~~α ⊃ β۳.
β ⊃ ~~β۴.
۳، ۴، قیاس شرطی~~α ⊃ ~~β۵.
۱ تا ۵(α⊃β) ⊢ (~~α ⊃ ~~β)۶.
۶ و IG⊂ ⊢(α⊃β) ⊃ (~~α ⊃ ~~β)۷.
ب(α⊃β) ⊃ (~~α ⊃ ~~β)۱
آ(~~α ⊃ ~~β) ⊃ (~β⊃~α)۲.
۱، ۲، قیاس شرطی(α⊃β) ⊃ (~β⊃~α)۳.

■ لم E۳:

~(α ⊃ β) ⊢ ( β ⊃ α)

برهان:

مقدمه~(α⊃β)۱.
ترانهش(β ⊃ (α⊃β)) ⊃ (~(α⊃β) ⊃ ~β) ۲.
E۱β ⊃ (α⊃β)۳.
۳، ۲، ⊃E~(α⊃β) ⊃ ~β۴.
۱، ۴، ⊃E~β۵.
سرریز~β ⊃ (β⊃α)۶.
۵، ۶، ⊃Eβ ⊃ α۷.

■ لم E۴:

(E۴): α ⊃ β, α ⊃ (β ⊃ γ) ⊢ α ⊃ γ

برهان:

مقدمهα⊃β۱.
مقدمهα⊃(β⊃γ)۲.
فرضα۳.
۳، ۲، ⊃Eβ⊃γ۴.
۳، ۱، ⊃Eβ۵.
۵، ۴، ⊃Eγ۶.
۱ تا ۶α⊃β, α⊃(β⊃γ ), α ⊢ γ ۷.
۷ و IG⊂ α⊃β, α⊃(β⊃γ ) ⊢ α ⊃ γ ۸.

■ لم E۵

(E۵): α ⊃ β, α ⊃ γ ⊢ α ⊃(β ∧ γ)

برهان:

مقدمه α ⊃ β۱.
مقدمهα ⊃γ۲.
فرض α۳.
۱، ⊃Eβ۴.
۱، ⊃Eγ۵.
۳، ۴، ∧Iβ ∧ γ۶.
۱ تا ۶α ⊃ β, α ⊃γ, α ⊢(β ∧ γ) ۷.
۷ و IG⊂ α ⊃ β, α ⊃γ ⊢ α ⊃ (β ∧ γ)۸.

■ قضیه دمورگان ↝

(De.M): ⊢ (~α ∨~β) ⊢ ⊣ ~(α ∧ β)

برهان:

۲- نشان می‌دهیم:⊢~(α∧β) ⊃ (~α∨~β)
∨I(~α) ⊃ (~α∨~β)۱.
∨I(~α) ⊃ (~α∨~β)۲.
۱، ترانهش~(~α∨~β) ⊃ α۳.
۲، ترانهش~(~α∨~β) ⊃ β۴.
۳، ۴، e۵~(~α∨~β) ⊃ (α∧β) ۵.
۵، ترانهش~(α∧β) ⊃ (~α∨~β)۶.
۱- نشان می‌دهیم:⊢(~α∨~β) ⊃ ~(α∧β)
مقدمه(~α) ∨ (~β)۱.
a۱α∧β ⊃ α۲.
a۲α∧β ⊃ β۳.
۲، ترانهش(~α) ⊃ ~(α∧β) ۴.
۳، ترانهش(~β) ⊃ ~(α∧β) ۵.
۱، ۴، ۵، ∨E~(α∧β)۶.

■ لم E۶ - E۷

E۷: (α∧~β) ⊢ ~(α⊃β)E۶: (α∧β)⊃γ, (α∧β)⊃~γ ⊢ α⊃~β

برهان:

E۷E۶
[α ∧ ~β ∧ (α⊃β)]⊃α۱.
[α ∧ ~β ∧ (α⊃β)] ⊃ (α⊃β) ۲.
[(α ∧ ~β) ∧ (α⊃β)]⊃~β۳.
۱، ۲، e۴[(α ∧ ~β) ∧ (α⊃β)]⊃β ۴.
۳، ۴، e۶(α ∧ ~β) ⊢ ~(α⊃β)۵.
مقدمهα∧β ⊃ γ۱.
مقدمهα∧β ⊃ ~γ۲.
فرض α۳.
۱-واگردان α ⊃ (β⊃γ)۴.
۲-واگردان α ⊃ (β⊃~γ)۵.
۳-۴-⊃Eβ ⊃ γ۶.
۳-۵-⊃Eβ ⊃ ~γ۷.
۶-۷-~I~β۸.
۱ تا ۸(α∧β) ⊃ γ, (α∧β) ⊃ ~γ,α ⊢ ~β۹.
 ۹-⊃IG(α∧β) ⊃ γ, (α∧β) ⊃ ~γ ⊢ α⊃~β۱۰.

■ لم E۸:

α⊃γ, β⊃γ ⊢ (α∨β)⊃γ

برهان:

فرض(α∨β)۱.
مقدماتα⊃γ, β⊃γ۲.
۱، ۲ و ∨Eα⊃γ, β⊃γ ⊢ γ۳.
۱ تا ۳ و ⊃IGα⊃γ, β⊃γ ⊢ (α∨β)⊃γ۴.

■ هم‌ارزی نقض دوگانه

⊢~~α ≡ α.

اثبات

طبق نفی دوگانه داریم: ⊢~~α⊃α. بنابراین، کافی است نشان دهیم:

⊢α ⊃ ~~α.

ساده گردان(α∧~α) ⊃ α۱.
ساده گردان(α∧~α) ⊃ ~α ۲.
۱، ۲، E۶α ⊃ ~~α۳.

■ قیاس اقترانی↝

α ⊃ β, ~β ⊢ ~α

برهان:

مقدمهα ⊃ β۱.
مقدمه~β۲.
ترانهش(α⊃β) ⊃ (~β⊃~α) ۳.
۱، ۳، ⊃E~β ⊃ ~α۴.
۲، ۴، ⊃E~α۵.

■ قضیه تبدیل

⊢(α ∨ β) ⊢ (~α ⊃ β)
⊢(~α ⊃ β) ⊢ (α ∨ β)

برهان:

۲- نشان می‌دهیم:⊢(α⊃β) ⊃ (~α∨β)
فرض(α⊃β)۱.
∨I۱~α ⊃ (~α∨β)۲.
∨I۲β ⊃ (~α∨β)۳.
۲، ترانهش~(~α∨β) ⊃ α۴.
۳، ترانهش~(~α∨β) ⊃ ~β۵.
۴، ۵ ، E۵~(~α∨β) ⊃ (α∧~β)۶.
E۷(α∧~β) ⊃ ~(α⊃β)۷.
۶، ۷، قیاس شرطی ~(~α∨β) ⊃ ~(α⊃β)۸.
۸، ۱(α⊃β) ⊃ (~α∨β)۹.
۱، ۹، ⊃E~α∨β۱۰.
از ۱ تا ۱۰(α⊃β) ⊢ (~α∨β)۱۱.
۱۱ و ⊃IG⊢(α⊃β) ⊃ (~α∨β)۱۲.
۱- نشان می‌دهیم:⊢(α∨β) ⊃ (~α⊃β)
فرضα∨β۱.
فرض~α۲.
۱، ~Eα⊃β ۳.
اینهمانی β⊃β ۴.
۱، ۳، ۴، ∨Eβ۵.
از ۱ تا ۵(α∨β), ~α⊢β ۶.
۶ و دو بار (I.C.G) ⊢(α∨β) ⊃ (~α⊃β)۷.

■ قضیه دوگانگی:

⊢α ∨ ~α

برهان

قضیه α ⊃ α۱.
تبدیل(α ⊃ α) ⊃ (~α ∨ α)۲.
۱، ۲، ⊃E~α ∨ α۳.

از این قضیه قاعده زیر با کوته نام L.E.M (برای Law of Excluded Middle) به دست می‌آید:


———L.E.M
⏉

■ تفکیک شرطی (⊃R):

(⊃R): α ⊃ β, ~α ⊃ γ ⊢ β ∨ γ

برهان:

مقدمه α ⊃ β۱.
مقدمه ~α ⊃ γ۲.
۱ و ترانهش~β ⊃ ~α۳.
۳، ۲ و قیاس فرضی~β ⊃ γ۴.
۴ و تبدیل~~β ∨ γ۵.
۵ نفی دوگانه وβ ∨ γ۶.

■ قیاس فصلی ↝ / ↝

α, ~α ∨ β ⊢ β

برهان:

مقدمهα۱.
مقدمه~α∨β۲.
۲، تبدیلα⊃β۳.
۱، ۳، ⊃Eβ۴.

■ پخش پذیری '∧' و '∨':

۱: (α ∧ β) ∨ γ ≡ (α ∨ γ) ∧( β ∨ γ)
۲: (α ∨ β) ∧ γ ≡ (α ∧ γ) ∨ (β ∧ γ)

برهان:

(α ∨ γ) ∧ (β ∨ γ) ⊢ (α ∧ β) ∨ γ.
تبدیل(α∨γ)∧(β∨γ) ⊢ (~α⊃γ)∧(~β⊃γ)۱.
تفکیک(⊃R)(~α⊃γ)∧(~β⊃γ) ⊢ (~α∨~β)⊃γ۲.
تبدیل(~α∨~β)⊃γ ⊢ ~(~α∨~β)∨γ۳.
دمورگان و نفی دوگانه~(~α∨~β)∨γ ⊢ (α∧β)∨γ۴.
از ۱ تا ۴ و ترایایی(α∨γ)∧(β∨γ) ⊢ (α∧β)∨γ۵.

برای بقیه حالات نیز می‌توان به همین ترتیب برهان آورد.

■ برهان خلف

(۱): ~α ⊢ ⊥ ⇒ α
(۱'): α ⊢ ⊥ ⇒ ~α

~α
.
.
.

⊥
———
α

برهان غیرمستقیم - کاهش به پوچ

Reductio Ad Absurdum (R.A.A)

α
.
.
.

⊥
———
~α

برهان:

~α ⊢ ⊥۱.
تعریف ⏊~α ⊢ χ ∧ ~χ۲.
۲، ⊃IG~α ⊃χ ∧ ~χ۳.
ساده گردانχ ∧ ~χ ⊃ χ۴.
ساده گردانχ ∧ ~χ ⊃ ~χ۵.
۲، ۴ و قیاس شرطی~α ⊃ χ۶.
۲، ۵ و قیاس شرطی~α ⊃ ~χ۷.
۶، ۷، ~I~~α۸.
۸، ~~Eα۹.

■ مجموعه‌های سازگار و ناسازگار فرمول‌ها

☚ در ادامه، S یک مجموعه فرمول در دستگاه NdPℓ است.

تعریف:

گوییم S یک مجموعه سازگار فرمول است اگر و فقط فرمول α به قسمی که α و ~α هر دو از S دستآوردنی باشند، وجود نداشته باشد. در غیر این صورت، S را یک مجموعه ناسازگار فرمول گوییم.

• مثال: مجموعه ناسازگار:

نشان می‌دهیم

Δ = {α ∧ (β ∨ δ), (~δ ∨ λ) ∧ (λ ⊃ ~λ), ~β}

یک مجموعه ناسازگار از فرمول است:

اثبات:

استنتاج عضویتی Δ ⊢ α ∧ (β ∨ δ) ۱.
Δ ⊢ (~δ ∨ λ) ∧ (λ ⊃ ~λ)۲.
Δ ⊢ ~β۳.
۱، ∧E Δ ⊢ (β ∨ δ)۴.
۳، ۴، قیاس فصلیΔ ⊢ δ۵.
۲، ∧EΔ ⊢ ~δ ∨ λ۶.
۲، ∧EΔ ⊢ λ ⊃ ~λ۷.
۵، ۶، قیاس فصلیΔ ⊢ λ۸.
۷، ۸، ⊃EΔ ⊢ ~λ۹.

بنابراین، فرمول λ به قسمی که λ و ~λ هر دو از Δ دست-آمدنی باشند، وجود دارد. پس، Δ بنا بر تعریف ناسازگار است.

■ نتیجه ناسازگاری

S ناسازگار است اگر و فقط اگر هر فرمولی‌ از آن دست-‌آمدنی باشد. به عبارت دیگر: S سازگار است اگر و فقط اگر فرمولی هست که از S دست-‌آمدنی نیست.

اثبات:

ازآنجاکه S ناسازگار است، فرمول α، به قسمی که S⊢α و S⊢~α،وجود دارد. گیریم χ یک شمای فرمولی، بنا به (آ) در زیر؛

مقدمهS ⊢ α۱.
مقدمهS ⊢ ~α۲.
۲، ~ES ⊢ α ⊃ χ ۳.
۱، ۳، ⊃ES ⊢ χ۴.(آ):

χ از S دست-‌آمدنی است. و نیز اگر هر فرمولی از S دست-آمدنی باشد پس α و ~α نیز از S دست-آمدنی هستند.

■ سازگاری و سازگاری مطلق

به ŞND (یا هر نظریه برهان) یک دستگاه استنتاجی سازگار گفته می‌شود اگر فرمول α به قسمی که α و ~α هر دو قضیه‌های آن دستگاه باشند وجود نداشته باشد.

بنا به قضیه ناسازگاری اگر فرمول‌های α و ~α قضیه‌های ŞND باشند آنگاه همه فرمول‌ها در ŞND قضیه خواهند بود.

دستگاهی که در آن، همه فرمول‌ها قضیه نباشند را مطلقاً سازگار گویند.

■ نتیجه ۱ سازگاری

۲S ناسازگار است.اگر و تنها اگرS ⊢⊥
۲'S سازگار است.اگر و تنها اگرS ⊬⊥

اثبات:

گیریم S ناسازگار، بنا به نتیجه یکم ناسازگاری، برای فرمول شماتیک χ داریم:

S ⊢ χ و S ⊢ ~χ.

 ازاینجا و بنا به (ب) در زیر؛

(ب): S ⊢ χ۱.
S ⊢ ~χ۲.
۱، ۲، ∧IS ⊢ χ ∧ ~χ ۳.

می‌توان نـوشت:

S ⊢ ⊥▢

به وارون، بـنا به ساده گردان:

اگــر S ⊢ ⊥ آنـگـاه S⊢χ و  S⊢~χ.

■ دو نتیجه ناسازگاری:

۱- S∪{~α} ناسازگار است اگر و فقط اگر S⊬α] .S ⊢ α اگر و فقط اگر S∪{~α} سازگار باشد.]

۲- S∪{α} ناسازگار است اگر و فقط اگر S⊬~α] .S ⊢~α اگر و فقط اگر S∪{α} سازگار باشد.]

اثبات:

↩گیریم S∪{~α} ناسازگار، نشان می‌دهیم S ⊢α. با توجه به فرض داریم:

(آ): S∪{~α}⊢α و نیز (ب): S∪{~α}⊢~α.

از (آ) و (ب) و کار زدن ⊃IG داریم:

S⊢~α⊃α و S⊢~α⊃~α.

از این دو و ~I آنچه می‌خواهیم حاصل است.

↪گیریم S ⊢ α، نشان می‌دهیم S∪{~α}ناسازگار است. از فرض و خاصیت یکنوایی داریم:

(آ): S∪{~α}⊢α.

بنا به استنتاج عضوی می‌توان نوشت:

(ب): S∪{~α}⊢~α.

(آ) و (ب) نتیجه می‌دهند که S∪{~α} ناسازگار است.

۲ را نیز به همین شیوه می‌توان اثبات کرد.

■ نتیجه مهم سازگاری

از ۱ به دست می‌آید:

اگر S سازگار باشد و فرمول α از S قابل استنتاج نباشد آنگاه با افزودن ~α به S ،S سازگار باقی می‌ماند.

■ بسته بودن استنتاجی

مجموعه فرمول S را تحت '⊢' بسته [یا، S را به گونه استنتاجی بسته] گویند اگر برای هر فرمول α به قسمی که S⊢α و α∈S.

مجموعه S تحت '⊢' بسته است اگر هر نتیجه S در S باشد.

☚ بنا به استنتاج عضویتی در دستگاه NdPℓ داریم: α∈S⇒S⊢α.

■ تئوری صوری

گیریم T یک مجموعه فرمول باشد. در این صورت، T را یک تئوری صوری [یا فقط یک تئوری / نظریه] در ŞND گوییم اگر T سازگار و به گونه استنتاجی بسته باشد.

■ قضیه فشردگی

مجموعه فرمول S سازگار است اگر و تنها اگر همه زیرمجموعه‌های متناهی آن سازگار باشند.

به عبارت دیکر (عکس نقیض):

مجموعه فرمول S ناسازگار است اگر و تنها اگر زیرمجموعه‌ای متناهی از آن ناسازگار باشند.

اثبات:

۱- گیریم S سازگار باشد. در این صورت همه زیرمجموعه‌های آن سازگار است. زیرا، اگر زیرمجموعه S' از آن باشد که ناسازگار باشد، آنگاه خواهیم داشت:

(۱): S' ⊢ α و S' ⊢ ~α.

از (۱) و یکنوایی داریم:

S ⊢ α و S ⊢ ~α

و این خلاف فرض است.

۲- گیریم همه زیرمجموعه‌های متناهی S سازگار باشند. نشان می‌دهیم S سازگار است.

اگر S ناسازگار باشد آنگاه α و ~α هر دو از S قابل استنتاج هستند. در این صورت برهان‌های ۱ و ۲ در زیر وجود دارند:

۱- α'۱, α'۲, . . . ,α'm-۱, α'm = ~α

و

۲- α۱, α۲, . . . ,αn-۱, αn = α

اکنون مجموعه S' را مطابق زیر تعریف می‌کنیم:

S' = S ∩ {α۱, α۲, . . . ,αn-۱, αn , α'۱, α'۲, . . . ,α'm-۱, α'm}

اکنون می‌گوییم:

یکم: S' متناهی است [اشتراک هر مجموعه با یک مجموعه متناهی، متناهی است] است.

دوم: S' زیرمجموعه S است.

سوم: S' ناسازگار است [چون α و ~α هر دو از S' قابل استنتاج هستند] و این خلاف فرض است.

■ سازگاری بیشینه

گیریم S مجموعه فرمول باشد. گوییم S سازگار بیشینه (Maximally consistent) است [یا دارای سازگاری بیشینه است] اگر و تنها اگر:

۱- S سازگار باشد؛ و

۲- برای هر مجموعه سازگار T اگر S ⊆T آنگاه S=T. [به‌عبارت‌دیگر، برای هر T به قسمی که S زیرمجموعه سره آن، آنگاه T ناسازگار باشد.]

■ نتیجه ۱ سازگاری بیشینه

گیریم S سازگار بیشینه باشد آنگاه S به گونه استنتاجی بسته است. [S یک تئوری است.]

اثبات:

فرض می‌کنیم S سازگار بیشینه باشد و داشته باشیم S⊢α. اگر α∉S آنگاه بنا به بند ۲ تعریف سازگاری بیشینه، مجموعه S∪{α} ناسازگار خواهد بود (چون S زیرمجموعه سره آن خواهد شد.) اما بنا به نتیجه ۳ ناسازگاری اگر S∪{α} ناسازگار باشد آنگاه S⊢~α. اما این خلاف فرض (S⊢ α و سازگاری S) است.

■ نتیجه ۲ سازگاری بیشینه

گیریم S سازگار بیشینه باشد، آنگاه برای فرمول دلخواه α داریم α∈S یا ~α∈S.

اثبات:

با توجه به سازگاری S می‌دانیم چنین نیست که α و ~α هر دو در S باشند. اکنون مجموعه:

T = S ∪ {α}

را در نظر می‌گیریم. T ناسازگار یا سازگار است.

(آ)ـ اگر T ناسازگار باشد بنا بر نتیجه ۱ ناسازگاری داریم: S⊢~α. اما طبق فرض S سازگار بیشینه است. بنابراین، بنا به نتیجه ۱ سازگاری بیشینه S بگونه استنتاجی بسته است؛ پس: ~α∈S.

(ب)ـ اگر T سازگار باشد ازآنجاکه S⊆T، بنا به بند ۲ تعریف سازگاری بیشینه داریم؛ S=T؛ پس: α∈S.

■ نتیجه ۳ سازگاری بیشینه

گیریم مجموعه فرمول S سازگار بیشینه، α و β نیز دو فرمول باشند. در این صورت داریم:

(آ): (α ⊃ β) ∈ S ⇔ (α ∈ S ⇒ β ∈ S)

α ⊃ β در S است اگر و تنها اگر α در S نباشد یا β در S باشد.↝

(ب): (α ∧ β) ∈ S ⇔ (α ∈ S و β ∈ S)

(ج): (α ∨ β) ∈ S ⇔ (α ∈ S یا β ∈ S)

اثبات:

(آ):
↩↪
مقدمهα∈S⇒β∈S ۱.
فرضα∈S۲.
۱، ۲ و ⊃Eβ∈S ۳.
۳ و P۴S⊢β۴.
۴ و E۱S⊢(α⊃β)۵.
۵ و بسته بودن S(α⊃β)∈S ۶.
فرضα∉S۷.
۷ و سازگاری بیشینه~α∈S۸.
۸ و بسته بودن SS⊢~α۹.
۹، ~ES⊢(α⊃β)۱۰
۱۰ و بسته بودن S(α⊃β)∈S ۱۱.
مقدمه(α⊃β)∈S ۱.
۱ و P۴S⊢(α⊃β)۲.
فرضα∈S۳.
۳ و P۴S⊢α۴.
۴، ۲، ⊃ES⊢β۵.
۵ و بسته بودن Sβ∈S ۶.
(ب):
مقدمهα∈S و β∈S۱.
۱ و P۴S⊢α, S⊢β ۲.
۲، ∧IS⊢α∧β۳.
بسته بودن Sα∧β∈S۴.
مقدمه(α∧β)∈S ۱.
۱ و P۴S⊢α∧β۲.
۲، ساده گردانS⊢α, S⊢β ۳.
بسته بودن Sα∈S, β∈S۴.
(ج):

با توجه به تبدیل، (ج) منجر به ~α⊃β می‌گردد که این به‌نوبه خود منجر به (آ) می‌شود. بنابراین: α∨β در S است اگر و فقط اگر ~α در S نباشد یا β در S باشد. اما بنا به نتیجه ۲ سازگاری بیشینه ~α در S نیست اگر و فقط اگر α در S باشد و ازاینجا نتیجه حاصل است.

■ نتیجه ۴ سازگاری بیشینه

برای هر مجموعه سازگار S، مجموعه سازگار بیشینه T وجود دارد، به قسمی که S زیرمجموعه T است

به عبارت دیگر: هر مجموعه سازگار درون یک مجموعه سازگار بیشینه است.

اثبات:

۱- از آنجا که ƒPℓ، مجموعه فرمول‌های NdPℓ، شمارا است پس می‌توان آن‌ها را برشمرد. فرض کنید فهرست l در زیر یک برشمارش از اعضای ƒPℓ باشد. [یعنی، هر عضو ƒPℓ در این فهرست وجود داشته باشد.]

l: α۰, α۱, α۲, . . .

۲- دنباله U=<un> را به شیوه بازگشتی مطابق زیر تعریف می‌کنیم:

دنباله
U
آ: u۰=
S
.
.
.
ب:un+۱={αn} ∪ un: اگر {αn} ∪ unسازگار باشد.
un: اگر{αn} ∪ unسازگار نباشد.

پس برای هر αk از فهرست l یک uk وجود دارد و نیز برعکس آن.

۳- مجموعه U* را برابر:

(m≥۰برای ) u۰∪u۱∪u۲∪ . . .∪um

گرفته. [پس برای هر αk یک uk وجود خواهد داشت و نیز برعکس.]

۴- آشکار است که

S = u۰⊆u۱⊆u۲⊆ . . .⊆um⊆U*.

اکنون می‌گوییم:

'۱- برای هر i≥۰ مجموعه ui سازگار است. این با توجه به فرض سازگاری S و نیز (ب) در تعریف U حاصل خواهد بود.

'۲- U* سازگار است. مطابق ب.۸.۸ U* سازگار است اگر و فقط اگر هر زیرمجموعه متناهی آن سازگار باشد. فرض کنید A یک زیرمجموعه متناهی U* باشد. اگر A⊆S که در این صورت بنا به فرض سازگار بودن A ،S سازگار خواهد بود.

گیریم A ⊄ S. می‌توان نوشت A=B'∪B به قسمی که:

B' ∩ S=∅ و B ⊆ S
[پس B سازگار است].

اکنون فرض می‌کنیم:

(|B'| = d≤n) B' = {φ۱, . . . ,φd}.

بنابراین:

A = {φ۱} ∪ . . . ∪ {φd} ∪ B

اما (j≤d) φj در فهرست l است. بنابراین،φj=αk∈U* .

بنا بر ۳ در بالا و اینکه φj∉S، به ازای αk عنصر uk از دنباله U وجود دارد.

اگر {φj = αk} ∪ uk سازگار نبود آنگاه φj در B' نبود. پس

uk+۱ = {φj = αk} ∪ uk

با توجه به ۴ در بالا و اینکه uf ؛A⊆U* وجود دارد به قسمی که:

{φj} ∪ B ⊆ uf [برای هر j≤d ؛j].

بنابراین، A سازگار است.

'۳- U* سازگار بیشینه است. اگر U* سازگار بیشینه نباشد، پس مجموعه فرمول سازگار T و جود دارد به قسمی که، U*⊆T. فرض می‌کنیم β عضوی از T باشد. نشان می‌دهیم β∈U*.

ازآنجاکه β یک عضو ƒLp است، باید یکی از عناصر فهرست l، به فرض αk، باشد. پس برای عدد طبیعی k داریم β=αk به قسمی که αk∈T. بنا بر ۳ در بالا به ازای αk عنصر uk از دنباله U وجود دارد و بعلاوه: uk⊆U*⊆T. ازاینجا و اینکه T سازگار است باید {αk}∪uk نیز سازگار باشد[توجه داریم که، uk⊆T و [αk∈T. پس بنا به روند ساختن عناصر U، باید uk+۱={αk}∪uk. این یعنی αk∈uk+۱، و چون uk+۱⊆U* پس αk=β∈U*. بنابراین، T همان U* است.■

■ در باره سازگاری NdPℓ

بنا بر نتیجه ۴ سازگاری بیشینه اگر ƒPℓ سازگار باشد آنگاه سازگار بیشینه هم است و در این صورت NdPℓ یک تئوری خواهد بود.

■ تعبیر و فرامنطق در NdPℓ

مراد از تعبیر در NdPℓ همان سازوارگی /Machinery است که در بند تعبیر در LC یادداشت "صورت و معنی در منطق گزاره‌ها‌" آمده است. ولی زبان دستگاه NdPℓ (یعنی Pℓ) به شرح زیر از زبان LC متفاوت است:

۱.در زبان دستگاه NdPℓ رابط "≡" یک واژه تعریف‌شده (انگاره تعریفی / انگاره آغازی) است.
۲.

با توجه به تعریف "⏉" و "⏊" در Pℓ برای هر تعبیر I داریم:

(⏉)I = درست و (⏊)I = نادرست.

بنابراین، "⏉" و "⏊" به ترتیب شِما‌های، توتولوژی و تناقض هستند.

مراد از فرامنطق (Metalogic) نیز همان است که در یادداشت "منطق و فرامنطق " آمده است.

یادآوری:

اثبات رابطه S, α ⊩ β  توسط مدل (در منطق گزاره‌ای جدول ارزش) انجام می‌شود. (رهیافت نظریه برهان)
اثبات رابطه S, α ⊢ β توسط آوردن برهان انجام می‌شود. (رهیافت نظریه مدل)

■ سازگاری دستگاه NdPℓ

برای نشان دادن سازگاری NdPℓ (به عبارت دیگر مجموعه ƒLp) ابتدا باید نشان داد (فرا)قضیه تمامیت در NdPℓ برقرار است. به عبارت دیگر باید ثابت کرد:

فرمول α در NdPℓ قضیه است، اگر و تنها اگر α توتولوژی باشد.↝

به عبارت دیگر:

هر توتولوژی یک قضیه است و هر قضیه یک توتولوژی است.

فرض می‌کنیم قضیه تمامیت در دستگاه NdPℓ برقرار و نیز α یک توتولوژی باشد. بنابراین، بنا بر قضیه تمامیت α یک قضیه NdPℓ است. اما نقیض یک توتولوژی یعنی ~α، نمی‌تواند یک توتولوژی باشد↝. پس ~α قضیه NdPℓ نیست. ازاینجا؛ فرمول α در NdPℓ وجود دارد به قسمی که α و ~α هر دو در NdPℓ قضیه نیستند. درنتیجه، NdPℓ سازگار است.

ما در بحث سیستم اصل موضوعی نظریه برهان (منطق گزاره‌ای) اثبات قضیه تمامیت در  منطق گزاره‌ای را ارائه خواهیم کرد و خواهیم دید این اثبات را اندکی طولانی‌تر می‌توان در دستگاه NdPℓ به کار برد.

■ ■ ■ ■ ■ ■ ■ ■

در اینجا بحث نظریه برهان در منطق گزاره‌ای کلاسیک (دستگاه استناج طبیعی) را به پایان می‌بریم.

◄ توجه: