نگارش صورت و الگوریتم آن در منطق
منطق و فرامنطق
درآمد به منطق
۱- سرآغاز | ۱۶- تعریف بازگشتی زیرفرمول |
۲- زبان صوری Pℓ: معرفی واژگان ابتدایی | ۱۷- استقرای ساختاری (Structural induction) و خوانش یکتای فرمول |
۳- نگارش صورت (تألیف لفظ) | ۱۸- رتبه فرمول |
۴- روند نگارش صورت | ۱۹- اثبات یکتایی شمای (خوانش یکتای) فرمول |
۵- تعریف بازگشتی صورت | ۲۰- سطح اولویت رابطها و حذف پرانتز از فرمول |
۶- دنباله پیکربندی | ۲۱- تصمیم پذیری فرمول خوش-ساخت به روش کاهش در منطق گزارهها |
۷- مثال: نگارش لفظ (دنباله پیکربندی) | ۲۲- الگوریتمِ تصمیم پذیری فرمول - روش کاهش |
۸- فرمول در منطق | ۲۳- آزمایشگاه منطق - الگوریتم و کد پایتون تصمیم پذیری فرمول - روش کاهس |
۹- فرمول شماتیک | ۲۴- رابط اصلی فرمول |
۱۰- فرمول اتمی | ۲۵- آزمایشگاه منطق - الگوریتم و کد پایتون شناسایی رابط اصلی فرمول و موئلفههای آن |
۱۱- شمارایی مجموعه فرمولها | ۲۶- درخت فراکافت فرمول |
۱۲- درجه فرمول | ۲۷- مثال برای درخت فراکافت |
۱۳- زیرفرمول | ۲۸- شناسایی درخت فراکافت (Parse tree) |
۱۴- شمای فرمول و زیرفرمول بیواسطه | ۲۹- آزمایشگاه منطق - الگوریتم و کد پایتون شناسایی درخت فراکافت |
۱۵- سه شمای فرمول |
■ سرآغاز
هدف این یادداشت نگاه نزدیک به روند ساخت یک زبان صوری و نشان دادن توانایی تصمیمگیری و خوانش یکتای آن است. به عبارت دیگر، ارائه الگوریتمی که بتواند به درستی به پرسش «آیا این یک عبارت خوش-ساخت در آن زبان است؟» برای هر عبارت دلخواه در یک زبان صوری، پاسخ آری نه دهد. بنابراین، این یادداشت فقط به نگارش صورت (نحو) در زبان صوری مربوط میشود. [برای تعریف دقیق "رشته"، "زبان" و "عبارت" اینجا را ببینید.]
یک زبان صوری مجموعهای از واژگان ابتدایی همراه با فهرست محدود از قواعد، موسوم به قواعد نحوی / Syntax rules (نیز قواعد ساخت / Construction rules) است، به قسمی که بهموجب این قواعد بتوان یک و فقط یک زیرمجموعه ناتهی و زیرمجموعه سره از عبارتهای زبان — که به آنها فرمولهای خوش-ساخت گفته میشود — ساخت و متمایز گردد.
☚ مجموعه قواعد نحوی یک زبان صوری را نیز قواعد نگارش صورت (یا نحو زبان صوری) مینامند.
در بند بعد یک زبان صوری خواهیم ساخت و آن را Pℓ مینامیم.
■ زبان صوری Pℓ: معرفی واژگان ابتدایی
واژگان ابتدایی Pℓ شامل اعضای سه مجموعه ازهم جدا (اتمها - رابطها - نمادهای ویژه) به قرار زیر است:
| ۱- | اتمها: به هر یک از عناصر مجموعه: `{p, q, r, s , t}` یک اتم Pℓ (یا فقط اتم) میگوییم. گرچه در اینجا فقط پنج اتم معرفی شده است ولی در صورت لزوم میتوان با کاربرد اندیس، مانند,`{p_۱, p_۲, . . ., p_n}` به هر تعداد دلخواه از آنها معرفی کرد. بهطورکلی مجموعه اتمها نامتناهی فرض میشود. گرچه شمارایی مجموعه اتمها ضروری نیست ولی آن را شمارا فرض میکنیم. بنابراین میتوان مجموعه اتمها را`{p_۱, p_۲, . . ., p_n, . . .}` نیز در نظر گرفت. |
| ۲- | رابطها: `{~, ⊃, ∧, ∨}` به عنوان رابطهای ابتدایی. [بجای نماد "•" نماد "∧" را برای رابط عطف بکار بردهایم.] |
| ۳- | نمادهای ویژه به قرار {) ,(} بهعنوان ابزار وابسته زبانی برای پرهیز از چند خوانشی. |
اجتماع سه مجموعه بالا را ΣPℓ نامیده و به رشتههای متناهی ΣPℓ عبارتهای زبان Pℓ میگوییم. بنابراین،
p)r ∧ p , p ∧ q , p
هر سه عبارتهای Pℓ هستند.
☚: میتوان هر نماد را با قرار دادن آن داخل دو گیومه نامگذاری کرد؛ مثل "~" (یا «~») و مانند آن.
■ نگارش صورت (تألیف لفظ)
همانطور که در بالا آمد، مراد ما در اینجا از نگارش صورت (تألیف لفظ / نحو) وضع قواعدی است تا بهموجب آنها یک و فقط یک زیرمجموعه ناتهی و سره از عبارتهای Pℓ، که ازاینپس آن را ƒPℓ را مینامیم، متمایز گردد.
■ روند نگارش صورت
قواعد عضویت در ƒPℓ و بهعبارتدیگر، تعریف ƒPℓ را به روش بازگشتی بیان میکنیم. این روش به طور گسترده در ریاضیات، منطق و دانش کامپیوتر استفاده میشود. ویژگیِ اینگونه تعریف که به آن تعریف سازنده هم میگویند، پیدایش مصداقهای معرَف (تعریفشده) در روند تعریف است.
هر تعریف بازگشتی در سهگام انجام میشود. بنابراین ƒPℓ را در سه گام به شرحی که خواهد آمد تعریف خواهیم کرد. ولی قبل از آن باید یک نکته را یادآوری کرد. و آن اینکه، قرار است یک زبان (زبان موضوع) تعریف شود و این بهوسیله زبان ناظر (فرازبان) که همین جمله در آن است، انجام میشود. بنابراین باید در زبان ناظر در باره "چیزهایی" در زبان موضوع سخن گفت. بهعبارتدیگر، نیاز است تا در زبان ناظر این "چیزها" را نام برد و به آنها ارجاع داد. در این موارد میتوان با قرار دادن عناصر زبان موضوع درون جفت گیومه آنها را متمایز کرد.
بعلاوه نیاز است چیزهایی را نام ببریم که گرچه در دامنه مصداقی مشخص هستند اما اشاره به مورد خاصی در این دامنه ندارند. مثل آنکه میخواهیم بگوییم «فرض کنید شئای یک عبارت Pℓ باشد، ...» یا «اگر شئای عضو ƒPℓ باشد، آنگاه....». در این موارد بهجای «شئای" از حروف کوچک الفبای یونانی بهقرار β ،α ،γ و λ با اندیس و بی اندیس استفاده خواهیم کرد. به اینها، که درواقع عناصر فرازبان هستند متغیرهای فرازبانی، گفته میشود.
■ تعریف بازگشتی صورت
در گام یکم (I) عبارتهای معینی از Pℓ را به صراحت به عضویت ƒPℓ درمیآوریم. به این نحو که میگوییم:
I: اتمها و ثابتهای منطقی عضو ƒPℓ هستند. (بنابراین ƒPℓ تهی نخواهد بود.)
در گام دوم (II) ƒPℓ را با یک پیوست چهار قاعدهای به شرحی که خواهد آمد گسترش میدهیم (با این چهار قاعده، عبارات بیشتری را برای ƒPℓ بر پایه عبارات موجود میسازیم).
پس میگوییم:
II.۱: اگر α عضو ƒPℓ باشد آنگاه ~α نیز عضو ƒPℓ است.
مثال: بنا بر I، اتم p عضو ƒPℓ است و بنا بر II.۱ عبارت ~p نیز عضو ƒPℓ خواهد بود. و ازآنجاکه p~ عضو ƒPℓ است، مجدداً بنا بر II.۱ عبارت p~~ نیز عضو ƒPℓ است. (با تکرار روند II.۱ به هر تعداد دلخواه میتوان برای ƒPℓ عضو ساخت.)
گام دوم را با وضع چهار قاعده دیگر تمام میکنیم و میگوییم:
اگر α و β عضو ƒPℓ باشند، آنگاه:
(α ∧ β) :II.۲
(α ∨ β) :II.۳
(α ⊃ β) :II.۴
عضو ƒPℓ هستند.
آنچه میماند اینکه این تعریف هنوز نهایی نیست (جامع است ولی مانع نیست). یعنی، آیا عبارتهای دیگر، غیر ازآنچه در این دو گام به عضویت ƒPℓ درآمدهاند، هستند که عضو ƒPℓ باشند؟ پس، گام آخر (سوم) نهایی کردن (بستن) تعریف (وضع قوانین تألیف لفظ) است.
بنابراین، در گام سوم(III)، میگوییم:
فقط آن عبارتها از Pℓ عضو ƒPℓ هستند که بهوسیله (I) و (II) ساختهشده باشند.
| ☚ | سهگانه بالا را قواعد نگارش Pℓ مینامیم. |
| ☚ | همیشه حرف آغازین اعضای ƒPℓ یک اتم یا "~" یا ")" است. |
■ دنباله پیکربندی
به دنبالهای متناهی از عبارتهای Pℓ دنباله پیکربندی گوییم اگر و تنها اگر هر یک از عناصر آن اتم (فرمول اتمی) باشند یا از عناصر قبلی و بناشده بر یکی از قواعد ساخت باشند. اکنون میتوان گفت:
α در Pℓ یک فرمول است اگر و تنها اگر یک دنباله پیکربندی که آخرین عنصر آن α باشد وجود داشته باشد.
دنباله پیکربندی یک فرمول الزاماً یکتا نیست. برای مثال:
| ☚ | ≺p, q, (p ∧ q)≻ و ≺q, p, (p ∧ q)≻ هر دو دنباله ساخت فرمول (p∧q) هستند. |
■ مثال: نگارش لفظ (دنباله پیکربندی)
نشان دهید عبارتهای زیر عضو ƒPℓ هستند.
۱- α = (~~ p ⊃ p)
۲- β = (((p ⊃ q) ∧ (q ∨ r)) ⊃ (p ∨ r)) ⊃ ~(q ∨ s)))
حل ۱: با توجه به فهرست زیر، α عضو ƒPℓ است.
| توجیه ساخت | عبارات ساخته | |
| اتمها عضو ƒPℓ هستند. (I) | p | ۱. |
| ۱ و II.۱. | ~p | ۲. |
| ۲ و II.۱. | ~~p | ۳. |
| ۳ و II.۴. | (~~ p ⊃ p) | ۴. |
| دنبالهای که عناصر آن عبارات ستون ۱ و به ترتیب از سطر ۱ تا ۴ است روند پیدایش (نگارش) اعضای ƒPℓ است. هر عضو این دنباله یک اتم است یا از عضوهای قبل بنا بر یک قاعده حاصلشده است. مراحل ۱ تا ۴ در بالا را میتوان بهصورت یک دنباله نشان داد: | ||
| ≺p, ~p, ~~p, (~~p ⊃ p)≻ | ||
حل ۲: با توجه به فهرست زیر، β عضو ƒPℓ است.
| توجیه ساخت | عبارات ساخته | ||
| I | p | ۱. | |
| I | q | ۲. | |
| I | r | ۳. | |
| I | s | ۴. | |
| ۱، ۲ و II | (p⊃q) | ۵. | |
| ۲، ۳ و II | (q∨r) | ۶. | |
| ۵، ۶ و II | ((p⊃q) ∧ (q∨r)) | ۷. | |
| ۱، ۳ و II | (p∨r) | ۸. | |
| ۲، ۴ و II | (q∨s) | ۹. | |
| ۷، ۸ و II | (((p⊃q)∧(q∨r)) ⊃(p∨r)) | ۱۰. | |
| ۹ و II | ~(q∨s) | ۱۱. | |
| ۱۰، ۱۱ و II | ((((p⊃q)∧(q∨r)) ⊃(p∨r))⊃~(q ∨s)) | ۱۲. | |
| در زیر روند ۱ تا ۱۲ در بالا بهصورت یک دنباله نشان دادهشده: | |||
| ≺ p, q, r, s, (p⊃q), (q ∨r), ((p⊃q)∧(q∨r)), (p∨r), (q∨s), (((p⊃q)∧(q ∨r))⊃(p ∨r)), ~(q∨s), ((((p⊃q)∧(q∨r))⊃(p∨r)⊃~(q∨s)) ≻ | |||
■ فرمول در منطق
زبان Pℓ را میتوان با معرفی عناصر جدید (برای مثال رابطها و اتمها از گونههای جدید) گسترش داد و زبان صوری بزرگتری را ساخت. این همان چیزی است که در تئوری سورها (فصل ۱۱ کتاب) انجام شد و اتمهای «ثابتهای انفرادی»، «حروف محمولی» و همچنین سه رابط «سور عمومی»، «سور وجودی» و «متغیر انفرادی» معرفی شدند. در این زبانها الفاظ تألیفی فقط "صورتهای گزارهای" آنگونه که در فصل نه کتاب معرفی شدند نیستند، بلکه صورتهای دیگر نیز به میان میآیند. منطق دانها به این صوَر «Well-Formed Formula» (با کوتهسازی wff) میگویند. ازآنجاکه در متون ریاضی به زبان فارسی عباراتی مانند «Well Defined» و «Well Ordered» به ترتیب به «خوش-تعریف» و «خوش-ترتیب» برگردانده شده است، ما نیز به پیروی «پیکره / پیکرک(ها)ی خوش-ساخت» یا آسانتر فرمول خوش-ساخت را با همان کوتهسازی، wff، بکار میبریم. و وقتی از زمینه مشخص است، فقط از "فرمول" یاد میکنیم. مراد از "خوش-ساخت" نابسته بودن آنها به هر تعبیری هستند که ممکن است به آنها منتسب گردد. حاصل کلام آنکه به عضوهای مجموعه ƒPℓ فرمولهای (خوش-ساخت) Pℓ میگوییم و فقط عضوهای این مجموعه را فرمولهای ƒPℓ مینامیم.
■ فرمول شماتیک
به فرمولی که در آن حداقل یک متغیر فرازبانی بهکاررفته، یک فرمول شماتیک گفته میشود. یک فرمول شماتیک معرفی تعداد نامتناهی فرمول است. برای مثال فرمول `(p∨α)` معرف `(p∨(p∧q))` یا `(p∨q)` و مانند آنها است.
■ فرمول اتمی
به یک فرمول غیر شماتیک که در آن رابطی بکار نرفته باشد فرمول اتمی و در غیر این صورت به آن فرمول غیر اتمی گفته میشود. بنابراین همه اتمها فرمول اتمی هستند.
■ شمارایی مجموعه فرمولها
• یادآوری از حساب (شماره گذاری گودل):
هر عدد طبیعی بزرگتر از یک را بهطور یکتا میتوان به عوامل اول تجزیه کرد. بهعبارتدیگر، برای هر n∈ℕ ; n>۱ اعداد متمایز اول
p۱, p۲ , . . . , pr [و تنها نیز آنها]
وجود دارند به قسمی که:
n = (p۱)a۱ × (p۲)a۲ × . . . × (pr)ar
که در آن:
ri ∈ ℕ; ri > ۱; a۱ ∈ ℕ; a۱ > ۰.
برای مثال:
۱۶,۵۲۹,۹۴۰,۸۶۴ = ۲۷ × ۳۱۷;
۱۰۰ = ۲۲ × ۵۲;
۶۳ = ۳۲ × ۷۱
و مانند آنها.
اکنون تابع g را طوری تعریف میکنیم که به نمادهای ابتدایی Pℓ اعداد زیر را نظیر کند:
g(()=۱ , g())=۲, g(~)=۳ , g(∧)=۴,
g(∨)=۵ , g(⊃)=۶ , g(p)=۷ , g(q)=۸,
g(r)=۹ , g(s)=۱۰ , g(t)=۱۱.
سپس به هر عبارت در Pℓ، مانند e → c۱c۲...cm، عدد:
۲g(c۱) × ۳g(c۲) × . . . × prg(cr)
را نظیر کرده به قسمی که در آن ci حرف iام در e و امینr ،pr عدد اول باشد. برای مثال، برای عبارت '(~∨~)' داریم:
(~∨~) ↔ ۲۱×۳۳×۵۵×۷۳×۱۱۲ = ۷۰۰۳۶۳۱۲۵۰
به این ترتیب، یک رابطه ۱:۱ بین زیرمجموعهای از اعداد طبیعی و عبارات Pℓ پدید میآید. و ازاینجا مجموعه عبارات Pℓ شمارا است؛ و چون مجموعه فرمولهای Pℓ، یعنی، ƒPℓ، زیرمجموعه عبارات آن است آنگاه ƒPℓ نیز شمارا است. اگر اتمهای Pℓ را نامتناهی و شمارا در نظر بگیریم، با توجه به نامتناهی بودن اعداد اول، هنوز ƒPℓ شمارا خواهد بود.
شمارایی ƒPℓ امکان برشمردن آن را میسر میسازد. بهعبارتدیگر، میتوان اعضای آن را به گونه زیر فهرست کرد:
α۱, α۲, α۳, . . . αk, . . .
به قسمی که هر عضو ƒPℓ در این فهرست باشد و هر αi یک عضو ƒPℓ باشد.
■ درجه فرمول
به تعداد رابطهای یک فرمول درجه فرمول میگویند. این عدد برابر با تعداد کار زدن قواعد II.1 تا II.4 در دنباله پیکربندی آن فرمول است. در مثالهای بالا رابطهای رنگی شده کار زدن یکی از قواعد ساخت II.1 تا II.4 را نشان میدهند.
■ زیرفرمول
فرض کنید `α` فرمول باشد. یک زیرفرمول (Subformula) α یک زیرعبارت α است اگر خود فرمول باشد. برای مثال اگر `α` فرمول `((p∨q)⊃p)` باشد آنگاه همه زیرفرمولهای α عبارتاند از:
`p, q, (p∨q), ((p∨q)⊃p)`
همانطور که دیده میشود، زیرفرمولهای یک wff همان عناصر دنباله پیکربندی آن هستند. بنابراین، به عناصر دنباله پیکربندی یک فرمول زیرفرمولهای آن فرمول میگویند.
در ادامه، ما در پی یک روند کارآمد برای یافتن زیرفرمولهای یک فرمول، به قسمی که ساختن دنباله ساخت آن را میسر کند خواهیم بود. در این راه و در قدم اول نیازمند به یک تعریف سازنده (بازگشتی) برای زیرفرمول هستیم. قبل از آوردن چنین تعریفی باید زیرفرمول بیواسطه را تعریف کنیم.
■ شمای فرمول و زیرفرمول بیواسطه
فرض کنید α یک wff غیر اتمی باشد. با توجه به قواعد پیکربندی درمییابیم که α به یکی از سه شمای زیر است:
۰ اتم (یکی از اعضای {p, q, r, s, t})،
یا
۱ ~β (~ موسوم به رابط یکتایی /Unary است)،
یا
۲ (γ b λ)؛ b یکی از رابطهای •, ∨, ⊃, ≡ (موسوم به رابطهای دوتایی /Binary است).
در شمای ۱، β را زیرفرمول بیواسطه α و در شمای ۲، γ و λ را زیرفرمولهای بیواسطه α مینامیم. بنابراین یک فرمول اتمی (شمای ۰) زیرفرمول بیواسطه ندارد و افزون بر آن یک فرمول زیرفرمول بیواسطه خود نیست.
■ سه شمای فرمول
با توجه به آنچه درباره زیرفرمول گفته شد، شمای یک فرمول Pℓ و زیرفرمول(های) بیواسطه آن را میتوان بهصورت زیر نیز نشان داد.
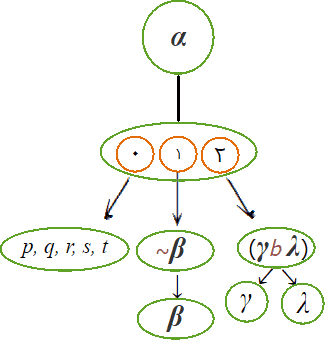
β, γ, λ در شمای ۱ و ۲ زیرفرمولهای بیواسطه α هستند.
به β, γ, λ مولفههای اصلی فرمول α نیز میگویند.
■ تعریف بازگشتی زیرفرمول
فرض کنید α یک wff باشد آنگاه:
| ۱. | α یک زیرفرمول α است؛ |
| ۲. | اگر β یک زیرفرمول α باشد، آنگاه همه زیرفرمولهای بیواسطه β زیرفرمول α هستند؛ |
| ۳. | فقط عباراتی که از ۱ یا ۲ به دست میآیند زیرفرمولهای α هستند. |
■ استقرای ساختاری (Structural induction) و خوانش یکتای فرمول
در بند قبل دیدیم هر فرمول در Pℓ به یکی از سه شمای (۰، ۱، ۲) است. آیا این شما یکتا است؟ بهعبارتدیگر، اگر فرمول α دارای دو شمای (γbλ) و (εbρ) باشد، آنگاه باید: ε= γ ،λ=ρ ؟
جواب این پرسش آری است و برای اثبات آن ابتدا باید با گونهای تکنیک برهان (در فرازبان) به نام استقرای ساختاری آشنا شد. در واقع، استقرای ساختاری گونهای تکنیک استدلال (تعمیم استقرای ریاضی) است که میتوان از آن برای اثبات ویژگیهای عناصر مجموعههایی که به روش استقرایی تعریف شدهاند (مانند مجموعه فرمولهای Pℓ، یعنی ƒPℓ) به کار زد.
یک استقرای ساختاری در دو گام انجام مییابد. در گام نخست نشان میدهیم ویژگی مورد نظر، به فرض P()، برای همه ساختارهای کمینهای در ƒPℓ برقرار است. در گام دوم نشان میدهیم که اگر ویژگی P() برای زیرساختارهای بیواسطه (ساختارهای کمینهای) آن ساختار برقرار باشد، آنگاه برای همه عناصر ƒPℓ نیز برقرار است.
⦁ استقرای ساختاری طولی (۱)
فرض کنید P() یک ویژگی (برای مثال زوج بودن تعداد پرانتزهای اعضای ƒPℓ) باشد. میخواهیم نشان دهیم این ویژگی برای همه اعضای ƒPℓ برقرار است. در چنین موارد کار زدن موفق استقرای طولی فرمول که بر اصل آمده در زیر استوار است برای شمول P() به همه اعضای ƒPℓ کافی است.
| ۱ | آ. P() بری هر فرمول اتمی در ƒPℓ برقرارباشد؛ |
| و | |
| ۲ | ب. اگر P() برای فرمول α برقرار است آنگاه برای ~α برقرار باشد؛ ج. اگر P() برای فرمولهای α و β برقرار است آنگاه برای (αbβ) برقرار باشد؛ |
⦁ مثال: زوج بودن تعداد پرانتزها در فرمول
اگر P ویژگی زوج بودن پرانتزها در ƒPℓ باشد، نیز x∈ƒLp باشد آنگاه داریم:
آ. P(x) برای هر {p, q, r, s, t} ∋ x؛
ب. اگر (فرمول λ و γ) P(λ) و P(γ) آنگاه P(~λ) و P(γbλ).
بنابراین، بنا به اصل استقرای ساختاری P برای همه اعضای ƒPℓ برقرار است.⦁ مثال: تعریف طول فرمول به روش بازگشتی
در بالا↥ طول یک فرمول را برابر طول عبارت آن گرفتیم. در زیر تعریف طول یک فرمول به شیوه تعریف بازگشتی آمده است. به شیوه استقرای طولی فرمول میتوان نشان داد مقدار طول فرمول در هر دو تعریف یکی است.
تابع len:ƒ𝓅ℓ →ℕ، آنگونه که در زیر تعریفشده را بهعنوان طول فرمول α میگیریم:
| len(α) = ۱ اگر α اتمی باشد؛ | |
| len(α) = l+۱ اگر α به شمای ~β و len(β)=l باشد؛ | |
| len(α) = l۱+ l۲+۳ اگر α به شمای (γbλ) و len(λ)=l۲, len(γ)=l۱ باشد؛ |
برای مثال:
۱- len(((p∧q)⊃r)) = len((p∧q)) + len(r) + ۳ = len(p) + len(q)+ ۳ + len(r) + ۳ = ۱ + ۱ + ۳ + ۱ + ۳ = ۹
۲- len((p∧q))=len(p) +len(q)+۳=۱+۱+۳=۵
⦁ استقرای ساختاری طولی (۲)
در زیر، بازآرایی دیگری از تعریف استقرای طولی فرمول آمده است که به آسانی میتوان نشان داد که با تعریف آمده در بالا↥ معادل است.
فرض کنید α فرمول و P() یک ویژگی آن باشد. میگوییم:
اگر P() برای هر فرمول با طول کوچکتر از |α| برقرار باشد آنگاه برای α نیز برقرار است. آنگاه P() برای هر عضو ƒLp برقرار است.
■ رتبه فرمول
رتبه فرمول معیاری برای اندازهگیری درجه ترکیب (پیچیدگی) یک فرمول است. در زیر تعریف رتبه فرمول به روش بازگشتی آمده است.
| اگر α فرمول اتمی باشد؛ | ۱ | ||||
| اگر α به شمای ~β باشد؛ | `Rank(β)+۱` | `Rank(α) =` | |||
| اگر α به شمای (γbλ) باشد. | `Max(Rank(γ), Rank(λ))+۱` | ||||
| تعریف تابع `Max(a, b)` | اگر `a>b` | `a` | `Max(a, b)=` | ||
| وگرنه | `b` | ||||
برای مثال:
۱- Rank(p)=۱
۲- Rank((p⊃q)) = Max(Rank(p), Rank(q)) + ۱ =
= Max(۱, ۱) + ۱=۱+۱ = ۲
۳- Rank(((p∧q)⊃r)) = Max(Rank((p∧q)), Rank(r)) +۱ =
= Max(۲, ۱) +۱ = ۲+۱=۳
۴- Rank(((p⊃q)⊃(p∧r))) = Max(۲, ۲) + ۱ = ۲+۱ = ۳
۵- Rank((((p∧(q∨r))⊃r)∨(p∧r))) = ۵
⦁ مثال: رتبه زیرفرمول
میخواهیم باکار زدن اصل استقرا تابت کنیم رتبه زیرفرمول یک فرمول، کوچکتر یا مساوی رتبه خود فرمول است.
حل:
برای اثبات، فرض استقرا را "رتبه هر زیرفرمول بیواسطه یک فرمول کوچکتر از رتبه خود آن فرمول است" گرفته و اثبات را ادامه میدهیم.
⦁ مثال: پاره آغازی سره (۱)
نشان دهید اگر پاره(ها) آغازی سره یک فرمول صرفاً شامل رابط "~" نباشد آنگاه تعداد پرانتز باز آن از تعداد پرانتز بسته آن بیشتر است.
⦁ مثال: پاره آغازی سره (۲)
نشان دهید پاره آغازی سره یک فرمول، خود فرمول نیست.
برای مثال فرمول (p∨q) را در نظر بگیرید. هیچیک از پاره(ها) آغازی سره آن، یعنی:
(, (p, (p∨, (p∨q
فرمول نیستند.
حل:
فرض کنید α فرمول باشد، نیز P() ویژگی "قطعههای آغازی سره همه فرمولهای با طول کوچکتر از |α| فرمول نیستند" باشد. P() را درست فرض میکنیم و میگوییم: α باید به یکی از سه شمای زیر باشد:
۰- α فرمول اتمی است و در این صورت قطعه آغازی سره ندارد.
۱- α به شمای ~β است. چنین فرض میکنیم ~β دارای قطعه آغازی سره است که فرمول است. این قطعه ~ نیست زیرا ~ فرمول نیست. پس قطعه آغازی ~β باید بهصورت ~β' باشد. این یعنی β' قطعه آغازی سره β است. اما طول β کوچکتر از طول ~β است و بنا بر P()، β' فرمول نیست. و ازآنجاکه قاعده ساختی β' را فرمول نمیکند، پس بنا به گام (III) در تعریف فرمول، ~β' فرمول نیست.
۲- α به شمای (γbλ) است. مانند حالت ۱ فرض میکنیم (γbλ) دارای پاره آغازی سره است که فرمول است. سپس به روش (۱) اثبات را ادامه میدهیم.
■ اثبات یکتایی شمای (خوانش یکتای) فرمول
فرض کنید α دارای دو شمای متفاوت (γbλ) و (εbρ) باشد ( γ و ε و نیز λ و ρ متفاوت از یکدیگرند و میدانیم ،γ ،ε λ و ρ فرمول هستند.) در این صورت ε باید قطعه آغازی سره γ یا برعکس باشد که هر دو حالت ممکن نیست. برای بقیه حالتها نیز به همین ترتیب است.
`top` و `bot` ثابتهای منطقیاند، مانند ۱ و ۰ در حساب: `top` توتولوژی و `bot` تناقض را نشان میدهند. معنای (تعبیر) آنها در یک سیستم منطقی ثابت است. آنها فرمولهایی هستند که به مقدار ارزش هیچ متغیری بستگی ندارند. (واژگان نامنطقی را نیز ببینید.)
۲- "≡" را برای کوتاه نویسی (یک رابط تعریفشده) مطابق تعریف زیر به کارخواهیم برد:
α ≡ β ≝ (α ⊃ β) ∧ (β ⊃ α)
توجه داریم که این نمادها هیچیک از نمادهای بنیادی زبان Pℓ نیست، بلکه هر یک طبق تعریف در Pℓ حاضرشدهاند.
■ سطح اولویت رابطها و حذف پرانتز از فرمول
فرض کنید میخواهیم عبارت ۲+۳×۴ را حساب کنیم. ابتدا ضرب (۳×۴) را را انجام میدهیم و بعد از آن جمع (۲+۱۲) را انجام خواهیم داد. دلیل این امر این است که ضرب سطح اولویت (یا تقدم) بالاتری نسبت به جمع دارد. این سطح اولویت را میتوان میتوان با پرانتز گذاری در ۲+۳×۴ به صورت ۲+(۳×۴) آشکار کرد. در منطق گزارهای، رابطها به همین شیوه کار میکنند. وقتی فرمولی با چندین رابط داریم، سطح اولویت آنها میگوید که عملیات باید به چه ترتیبی گروهبندی و ارزیابی شوند.
با معرفی مفهوم سطح الویت رابط آنگونه که در ادامه آمده و وضع قرارداد میتوان تا جایی که خواندن فرمول آسانتر میشود پرانتزها را حذف کرد و در صورت لزوم به هر اندازه پرانتز بارگذاری کرد. در زیر یک سلسله مراتب اولویت استاندارد برای رابطهای منطق گزارهای، از بالاترین اولویت (ابتدا انجام شود) تا پایینترین اولویت (آخر انجام شود) آمده است:
نقض (~): این رابط یکتایی فقط برای عبارتی که بلافاصله پس از آن میآید، اعمال میشود.
عطف (`^^`): این رابط، پیوند تنگتری نسبت به فصل (`vv`)، استلزام مادی (`sup`) یا دوشرطی (`-=`) برقرار میکند.
فصل (`vv`): این رابط، پیوند تنگتری نسبت به استلزام مادی (`sup`) یا دوشرطی (`-=`)، اما ضعیفتر از نقض و عطق، برقرار میکند.
استلزام مادی (`sup`): این رابط، اولویت کمتری نسبت به عطف و فصل دارد.
دو شرطی (`-=`): این رابط کمترین اولویت را دارد.
طبق قرارداد همیشه میتوان بیرونیترین جفت پرانتز فرمول را حذف کرد. برای مثال `p vv q` بهجای `(p vv q)` و مانند آن.
در زیر جدول سطح الویت رایطها آمده است.
| شرکتپذیری | رابط | سطح الویت |
| راست به چپ | ~ | "۰" |
| چپ به راست | ∧ | "۱" |
| چپ به راست | ∨ | "۲" |
| چپ به راست | ⊃ | "۳" |
| چپ به راست | ≡ | "۴" |
جدول آ.۱۰.۱ سطح الویت رابطها
توجه: مقدار اولویت با سطح اولویت نسبت وارون دارد. برای مثال در این جدول سطح اولویت "۰" بالاترین اولویت و سطح اولویت "۴" پائینترین اولویت است.
در مثالهای زیر نحوه کار زدن سطح الویت رابطها برای حذف و نیز بازگذاری پرانتز آمده است.
| ۱. | `p^^qvvrsups` ↔ `(p ^^ q) vv r sup s` ↔ `((p ^^ q) vv r) sup s` ↔ `(((p ^^ q) vv r) sup s)` |
| ۲. | `~ ~p` ↔ `~(~p) ↔ (~(~p))` |
| ۳. | `p sup q sup p` ↔ `(p sup q) sup p` ↔ `((p sup q) sup p)` |
| ۴. | `p vv
~(q sup p vv q)` ↔ `p∨~(q sup (p vv q))` ↔ ↔ `p vv (~(q sup (p vv q)))` ↔ ↔ `(p vv (~(q sup (p vv q))))` |
| ۵. | `p
sup ~q sup r` ↔ `q sup (~q) sup r` ↔ ↔ `(q sup (~q)) sup r` ↔ `(q sup (~q)) sup r` |
باید توجه داشت که نمیتوان با استفاده از مفهوم سطح الویت همه پرانتزهای هر فرمولی را حذف کرد. برای مثال حذف پرانتزهای p⊃(q⊃p) به فرمول p⊃q⊃p منجر میشود. بارگذاری پرانتزهای فرمول اخیر با توجه به سطح اولویت رابطها فرمول ((p⊃q)⊃p) را به دست میدهد که متفاوت از فرمول اول است. البته با بهرهگیری از روش نگارش موسوم به پولیش (لهستانی - Polish) میتوان بهتمامی از پرانتز در نوشتن فرمول خودداری کرد. در جای لازم از این روش بهره خواهیم برد. در نگارش به روش پولیش وقتی طول یک فرمول حتی کم هم باشد خواندن و نوشتن آن برای آدمیزاده با دردسر همراه است و البته خواندن آن برای ماشین بسی بیدردسر است.
■ تصمیم پذیری فرمول خوش-ساخت به روش کاهش در منطق گزارهها
در اینجا میخواهیم بدانیم آیا مسئله فرمول بودن در LC تصمیمپذیر است؟ بهعبارتدیگر اگر ρ یک عبارت دلخواه LC و |ρ|>۰ باشد آنگاه الگوریتمی هست که ورودی آن ρ و خروجی آن پاسخ آری یا نه درباره فرمول بودن (خوش-ساخت بودن / به قاعده ساخت) ρ باشد؟
برای مثال وقتی ورودی این الگوریتم هر یک از عبارات زیر باشد؛
۱- ((
۲- ((~p)
۳- )p(
۴- (p⊃((p⊃p)⊃(p⊃p)⊃(p⊃p))))
خروجی الگوریتم باید "نه" باشد؛ و برای ورودیهای زیر و مانند آنها؛
۱- (p⊃~q)
۲- p
۳- (p⊃((p⊃r)⊃((q•~p)⊃(p⊃s))))
باید "بله" باشد.
■ الگوریتمِ تصمیم پذیری فرمول - روش کاهش
این الگوریتم را کاهش فرمول مینامیم. الگوریتم کاهش فرمول (formula_reduction_algorithms / Fra) به عنوان ورودی یک عبارت (formula) در زبان Pℓ را میپذیرد و درستی نگارش (syntax correctness) آن را (true / false) برمیگرداند:
bool formula_reduction_algorithms(formula)
در عمل برای وارسی درستی نگارش فرمول از روشی (الگوریتمی) به نام فراکافت فروسویی بازگشتی (Recursive Descent Parser) استفاده میشود. پایینتر در قسمت «شناسایی درخت فراکافت»، ساختار و پیمایش درخت فراکافت آمده است.
توجه: همزمان با ارائه الگوریتم، اجرای آن را برای:
ρ:: `(p sup (~p sup q))`
پی خواهیم گرفت.
۰- z را اتمی میگیریم که در ρ نباشد؛ [مجموعه اتمها را شمارش پذیر نامتناهی فرض کردهایم و بعلاوه هر نماد در یک عبارت که پرانتز و رابط نباشد اتم خواهد بود.]
۱- z را جایگزین هر مورد اتمهای ρ میکنیم و حاصل را A۱ نامیده. این عمل را f۱ مینامیم. بنابراین:
A۱=f۱(ρ) =f۱((p⊃(~p⊃q)))=(z⊃(~z⊃z)
۲- z را جایگزین هر رویداد ~z در A۱میکنیم و حاصل را A۲ نامیده. این عمل را f۲ مینامیم. روشن است که: |A۲|≤|A۱|.
A۲ =f۲(A۱)=(z⊃(z⊃z))
۳- A۲ را از چپ به راست کاویده و اولین زیرعبارت یافته در آن به شمای (zbz) را با z جایگزین کرده. حاصل را A۳ نامیده. روشن است که: |A۳|≤|A۲|. این عمل را f۳ مینامیم.
A۳ =f۳(A۲)= (z⊃z)
۴- دستورالعملهای ۲ و ۳ را به ترتیب (یعنی، f۳ºf۲ که آن را f۴ مینامیم) برای A۳ تکرار میکنیم و حاصل را A۴ نامیده. این کار را تا جایی که، به فرض دربار nام، نتیجه بهدستآمده روی An با خود An یکی شود، یا بهعبارتدیگر داشته باشیم f۳ºf۲(An)=An ادامه میهیم. روشن است که در هر بار |An|<|An-۱| و دربار آخر |An+۱|=|An|.
A۴ =f۳ºf۲(A۳)=f۳ºf۲((z⊃z))=z
A۵ =f۳ºf۲(A۴)=A۴
۵- اگر An=z آنگاه ρ فرمول و در غیر این صورت فرمول نیست.
چون برای n=۴ داریم: A۴ =z پس ρ یعنی عبارت(p⊃(~p⊃q)) فرمول است.
توضیح: برای اثبات کارآمدی روند بالا (یعنی الگوریتم بودن آن) باید نشان داد اگر ρ فرمول باشد آنگاه عدد طبیعی n به قسمی که An=z وجود دارد (یعنی، اجرای الگوریتم در زمان محدود پایان میپذیرد که با توجه متناهی بودن طول عبارت ثابت میشود) و بعلاوه نیز نشانداد که اگر عدد طبیعی n به قسمی که An=z باشد وجود داشته باشد آنگاه ρ فرمول است و در غیر این صورت ρ فرمول نیست (یعنی اثبات صحت الگوریتم، که این نیز یا توجه به خوانش یکتای فرمول اثبات میشود).
مثال بیشتر:
ρ :: (p⊃((p⊃p)⊃~(p⊃p)⊃(p⊃~p))))
A۱ =f۱(ρ)=(z⊃((z⊃z)⊃~(z⊃z)⊃(z⊃~z))))
A۲=f۲(A۱)=(z⊃((z⊃z)⊃~(z⊃z)⊃(z⊃z))))
A۳=f۳(A۲)=(z⊃(z⊃~(z⊃z)⊃(z⊃z))))
A۴=f۳(A۳)=(z⊃(z⊃~z⊃(z⊃z))))
A۵=f۲(A۴)=(z⊃(z⊃z⊃(z⊃z))))
A۶=f۳(A۵)=(z⊃(z⊃z⊃z)))
A۷=f۳ºf۲(A۶)=(z⊃(z⊃z⊃z)))=A۶
فرمول نیست. ρ پس A۶=A۷≠z چون
ρ :: (p⊃((p⊃~p)⊃(p • p)⊃(p∨~p))))
A۱=f۱(ρ)=(z⊃((z⊃~z)⊃((z • z)⊃(z∨~z))))
A۲=f۲(A۱)=(z⊃((z⊃z)⊃((z • z)⊃(z∨z))))
A۳= f۳(A۲)=(z⊃(z⊃((z • z)⊃(z∨z))))
A۴= f۴(A۳)=(z⊃(z⊃(z⊃(z∨z))))
A۵= f۴(A۴)=(z⊃(z⊃(z⊃z)))
A۶= f۴(A۵)=(z⊃(z⊃z))
A۷= f۴(A۶)=(z⊃z)
A۸=f۴(A۷)=z
A۹=f۴(A۸)=A۸
فرمول است. ρ پس A۸=A۹=z چون
■ آزمایشگاه منطق - الگوریتم و کد پایتون تصمیم پذیری فرمول - روش کاهس
آزمایشگاه
برای ورود به آزمایشگاه درستی نگارش فرمول به روش کاهش دکمه را کلیک کنید.
■ رابط اصلی فرمول
فرض کنید α یک فرمول غیر اتمی، آنگاه α به یکی از دو شمای:
۱- ~β یا ۲- (γ b λ)
است. در شمای ۱ به ~ و در شمای ۲ به b رابط اصلی فرمول α گفته میشود. با توجه به یکتایی شمای فرمول، رابط اصلی فرمول نیز یکتاست. بنابراین، هر فرمول غیر اتمی دارای یک و فقط یک رابط اصلی است.
■ شناسایی رابط اصلی
فرض کنید α به شمای (γbλ) باشد. ازآنجاکه γ فرمول است پس باید تعداد پرانتزهای چپ و راست آن برابر و درنتیجه تعداد پرانتزهای چپ در "(γ" یک واحد بیشتر از پرانتزهای راست آن است. اما هیچ رابط دوتایی دیگر در " (γ" دارای این ویژگی نیست. بنابراین رابط اصلی یک فرمول به شمای (γbλ) اولین رابط دوتایی است که در زیر-عبارت بلافاصله مقدم آن (سمت چپ) دقیقاً دارای یک پرانتز چپ بیشتر از پرانتزهای راست آن باشد.
■ الگوریتم شناسایی رابط اصلی فرمول و موئلفههای آن
یافتن رابط اصلی یک فرمول منطق گزارهای برای درک ساختار و ارزیابی آن بسیار مهم است. در اینجا الگوریتمی برای یافتن رابط اصلی یک فرمول ارائه میکنیم. این الگوریتم را «FormulaStructure» مینامیم. ورودی این الگوریتم، «formula»، یک فرمول و خروجی آن رابط اصلی فرمول، زیرفرمول (زیرفرمولهای چپ و راست یا فقط چپ اگر رابط اصلی یکتایی باشد) یا یک خطا در صورتی که فرمول بد نوشته شده باشد، است.
■ شرح الگوریتم
این الگوریتم
به عنوان ورودی یک فرمول خوش-ساخت ر میپذیرد و آن را به بخشهای اصلیاش (سه شمای فرمول) به قرار زیر افراز میکند:
۱. "رابط اصلی" فرمول
را پیدا میکند،
۲.
زیرفرمول های سمت چپ و راست رابط اصلی را مییابد،
۳. اگ فرمول با (~) شروع شده باشد، دامنه اثر آن را برمیگرداند،
۴. اگر هیچ
رابطی وجود نداشته باشد، فرمول را به عنوان فرمول اتمی شناسایی میکند.
توضیح گام به گام:
تعریف رابطها:
• معرفی رابطها (Connectives): {~, &, |, ⊃, =}
• معرفی رابطهای دوتایی (Binary Connectives): {&, |, ⊃, =}
مقدمات
• حذف بیرونیترین پرانتزهای فرمول ورودی (پرانتزهای اضافی). برای مثال برگردان `((p & q))` به `p & q`:
• اگر فرمول ورودی دارای رابط نیست آنگاه به عنوان فرمول اتمی شناسایی میشود.
• تابع FormulaStructure به شرحی که میآید در پی یافتن رابط اصلی فرمول است:
این تابع از سمت چپ نویسههای فرمول را میپیماید و عمق عبارت داخل زوج پرانتزها «()» را حساب و در «depth» ذخیره میکند.
اگر نویسهای را که میپیماید پرانتز باز «(» باشد آنگاه پویش نویسهها وارد یک عبارت پرانتزی شده است و عمق («depth») افزایش مییابد.
اگر نویسهای را که میپیماید پرانتز بسته «)» باشد آنگاه به انتهای عبارت پرانتزی رسده است و عمق («depth») کاهش مییابد.
اگر نویسهای را که میپیماید رابط دوتایی باشد و داخل عبارت پرانتزی نباشد، یعنی «depth» صفر باشد، این رابط میتواند رابط اصلی باشد.
رابط اصلی با کمترین اولویت به شرح زیر کاوش میشود:
اگر چندین رابط خارج از پرانتز وجود داشته باشد، رابط اصلی، رابطی است که باید آخرین بار ارزیابی شود (دارای کمترین «اولویت»).
اگر رابط اصلی پیدا شود:
الگوریتم فرمول را به دو قسمت تقسیم میکند: چپ، راست و رابط اصلی. نتایج برگردانده میشود.
اگر هیچ رابط دودویی وجود نداشت: اگر فرمول با «~» شروع شود، «~» جدا شده و قلمرو اعمال آن تعین میشود.
اگر «~» و چیز دیگری برای جدا کردن وجود نداشته باشد، این یعنی فرمول اتمی است.
■ کد الگوریتم
function FormulaStructure(formula):
Connectives= {~, &, |, ⊃, =}
Binary Connectives={&, |, ⊃, =}
formula = removeOutermostParentheses(formula)
depth = 0
mainConnective = null
mainPosition = -1
lowestPrecedence = ∞ //Max-Integer
for i from 0 to length of formula - 1:
{
char = formula[i]
if char == '(':
depth += 1
else if char == ')':
depth -= 1
else if depth == 0 and char is a binary connectives:
precedence = getPrecedence(char)
if precedence <= lowestPrecedence:
lowestPrecedence = precedence
mainConnective = char
mainPosition = i
}
if mainConnective is not null:
left = substring(formula, 0, mainPosition).trim()
right = substring(formula, mainPosition + 1).trim()
return (mainConnective, mainPosition, left, right)
else if formula starts with '~':
subformula = substring(formula, 1).trim()
return ('~', 0, subformula, null)
else:
return (null, -1, null, null) // Atomic proposition
■ آزمایشگاه منطق - الگوریتم و کد پایتون شناسایی رابط اصلی فرمول و موئلفههای آن
آزمایشگاه
برای ورود به آزمایشگاه کد پایتون شناسایی رابط اصلی فرمول و موئلفههای آن دکمه کلیک کنید.
 توجه: با گسترش
FormulaStructure(formula)، یعنی کارزدن آن
به
روش بازگشتی تا رسیدن به فرمول اتمی، میتوان
درخت پیکربندی
فرمول را ساخت.
توجه: با گسترش
FormulaStructure(formula)، یعنی کارزدن آن
به
روش بازگشتی تا رسیدن به فرمول اتمی، میتوان
درخت پیکربندی
فرمول را ساخت.
■ درخت فراکافت فرمول:
در این بند به نگارش و خوانش فرمول (wff) در یک ساختار درختی (نمودار درختی) میپردازیم. به چنین ساختاری درخت فراکافت - Parse tree (یا درخت پیکربندی - Formation tree) گفته میشود.
در منطق، دو اصطلاح «درخت پیکربندی / Formation tree» و «درخت فراکافت / Parse tree» یک فرمول منطقی اغلب به جای یکدیگر برای اشاره به به مصداقهای مشابه، به ویژه در زمینه منطق گزارهای و منطق مرتبه اول، استفاده میشوند. هر دویِ آنها ساختار نحوی یک فرمول خوش-ساخت را نشان میدهند و نشان میدهند که چگونه از فرمولهای اتمی و رابطهای منطقی ساخته شده است. با این حال، میتوان تمایز ظریفی را قائل شد:
درخت فراکافت - Formation tree:
یک «درخت پیکربندی» فرآیند ساخت سیستماتیک یک فرمول خوش-ساخت بر اساس قواعد نحوی خاص را برجسته میکند. از نظر مفهومی، این رویکرد، رویکردی از پایین به بالا را نشان میدهد که در آن اجزای سادهتر به تدریج در عبارات پیچیدهتر جمع میشوند.
درخت فراکافت - Parse tree:
یک «درخت فراکافت»، تجزیه سلسله مراتبی یک فرمول خوش-ساخت به اجزای تشکیلدهنده آن را نشان میدهد. از نظر مفهومی، این رویکرد، رویکردی از بالا به پائین را نشان میدهد که در آن یک انگاره به تدریج به عبارات سادهتر فراکافت (تحلیل / تجزیه) میشود.
برای بسیاری از دستگاههای منطقی، ساختارهای درختی حاصل یکسان یا تقریباً یکسان هستند و این تمایز را در عمل کمتر مهم میکند. هر دو نوع درخت برای نمایش دیداری رابط اصلی یک فرمول و زیرفرمولهای آن عمل میکنند و به درک ساختار فرمول و ارزیابی مقدار ارزش آن کمک میکنند.
فرض میکنیم α فرمول باشد. درخت فراکافت α یا Treeα - را به گونه بازگشتی مطابق زیر تعریف میکنیم:
آ- اگر α اتمی باشد آنگاه؛
| Treeα=۰ α |
ب- اگر α به شمای ~β باشد آنگاه؛
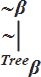 | Treeα= |
ج- اگر α به شمای (γbλ) باشد آنگاه؛
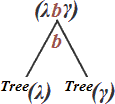 | Tree (γbλ)= |
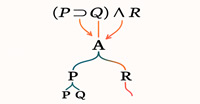
■ مثال برای درخت فراکافت
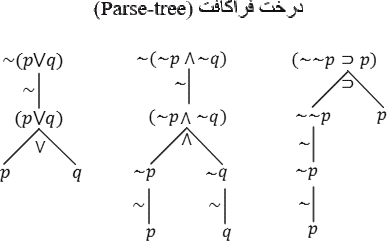
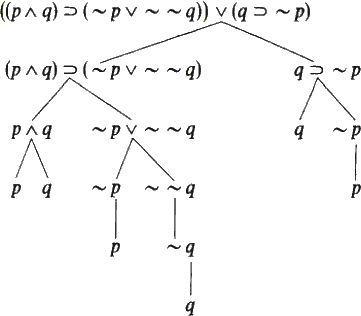
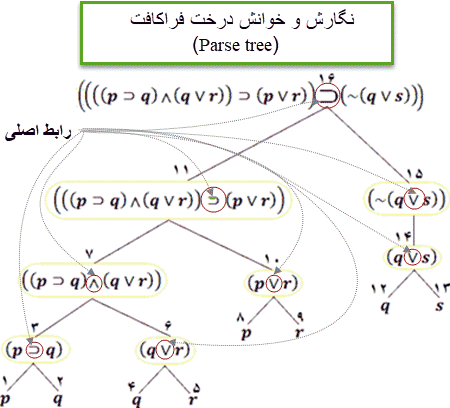
■ شناسایی درخت فراکافت (Parse tree)
فرض کنید T یک درخت دودویی باشد بهگونهای که؛
۱- محتوی هر برگ (گره انتهایی) یک اتم باشد؛
۲- محتوی هر گره ساده T یک فرمول به شمای ~β بوده و بعلاوه فرزند این گره دارای محتوی β باشد؛
۳- محتوی هر گره انشعاب در T فرمولی به شمای (γbλ) بوده و بعلاوه فرزندان چپ و راست این گره به ترتیب دارای محتوی γ و λ باشد؛
در این صورت به T یک درخت پیکربندی میگوییم. میتوان نشان داد که T متناظر با درخت پیکربندی فرمولی است که محتوای ریشه T است.
■ آزمایشگاه منطق - الگوریتم و کد پایتون شناسایی درخت فراکافت
توجه: همانطور که در بالا گفته شد (اینجا) با گسترش برنامه FormulaStructure(formula)، یعنی کارزدن آن به روش بازگشتی تا رسیدن به فرمول اتمی، میتوان درخت فراکافت فرمول را ساخت.
الگوریتم: ParseTree(formula):
// فرض میکنیم formula به عنوان ورودی تابع یک فرمول گزارهای با نگارش (نحو) صحیح باشد. برای الگوریتم وارسی نگارش فرمول به الگوریتم کاهش رجوع کنید.
گام ۱: رابط اصلی و زیرفرمولهای آن را پیدا کنید.
// رجوع به الگوریتم شناسایی رابط اصلی و موئلفههای آن
[MainConnective, LeftSubFormula, RightSubFormula] ⇐ MainConnective(formula)
گام ۲: مدیریت حالت پایه در روند بازگشت: رسیدن به یک فرمول اتمی. اگر رابط اصلی وجود نداشته باشد، فرمول یک فرمول اتمی (متغیر) است:
یک گره جدید ایجاد شود.
نوع گره را 'اتمی' بگذارید.
مقدار گره را خود فرمول قرار دهید (مثلاً 'P').
این گره را بعنوان خروجی تابع برگردانید.
گام ۳: ادامه روند بازگشتی برای: نقیض. اگر رابط اصلی '~' باشد، یک زیرفرمول تک داریم:
یک گره جدید ایجاد کنید.
نوع گره را 'نقیض' بنامید.
مقدار گره را '~' قرار دهید.
به صورت بازگشتی درخت را برای زیر-فرمول بسازید:
آن را به عنوان فرزند گره جاری قرار دهید.
فرزند این گره را ParseTree(LeftSubFormula) قرار دهید.
این گره را بعنوان خروجی تابع برگردانید.
گام ۴ (وگرنه): ادامه روند بازگشتی برای: یک رابط دوتایی.
یک گره جدید ایجاد کنید.
نوع گره را 'دوتایی' بنامید.
مقدار گره را MainConnective قرار دهید.
به صورت بازگشتی درختها را برای هر دو زیرفرمول بسازید و آنها را به عنوان فرزندان گره فعلی قرار دهید.
فرزند چپ گره را ParseTree(LeftSubFormula) بگیرید.
فرزند راست گره را ParseTree(RightSubFormula) بگیرید.
این گره را بعنوان خروجی تابع برگردانید.
آزمایشگاه
برای ورود به آزمایشگاه الگوریتم شناسایی درخت فراکافت دکمه کلیک کنید.

