≡
فهرست:
تابع و ماشین جهانی / Universal Function and machine درآمدی یه منطق

توابع بازگشتی جزئی و ماشین جهانی (Partial Recursive Functions)

منطق و نظریه رایانش (۴)

درآمد به منطق

همه جواهر هریک در جهان جدای خود است و هیچ وجه مشترک بین آنها نیست. مگر مفهوم جهانی جوهر. بنابراین، هیچ جواهری نیست که در جهان جدای خود نباشد. و به همین ترتیب، هیچ مفهوم جهانی نیست که در یک جوهر خاص نباشد↧. لایب نیتس.

SCHNEIDERS, W. (1971). , Leibniz' doppelter Standpunkt. Studia Leibnitiana, 161-190

در قسمت ماشین‌های اندوختگانی، ماشینی↝ را دیدیم که مدلی از یک تابع جزئی سره بود. ویژگی چنین ماشین‌هایی این است که برای ورودی‌های دامنه تابعی که قرار است رایانش شوند متوقف می‌شوند. اما، زمانی که ورودی در دامنه تابع نباشد، هرگز متوقف نمی‌شوند. این بدان معناست که ماشین‌های اندوختگانی چیزی بیشتر از این هستند که فقط مدل‌هایی از توابع معمولی↝ باشند. در این قسمت مفهوم بازگشتی را به «بازگشتی جزئی» گسترش خواهیم داد و سرانجام «تابع جهانی» و «ماشین جهانی» را معرفی خواهیم کرد.

روند منطق و نظریه رایانش (۴): توابع بازگشتی جزئی و ماشین جهانی

≡

۱- مقدمه

۶- تابع (جزئی) قطری (Diagonal partial function)

۲- توابع بازگشتی جزيی (Parial recursive functionc)

۷- روش قطری در اثبات وجود تابع کامل رایانش‌نا‌پذیر.

۳- نمایه‌سازی توابع رایانش‌پذیر جزئی (Indexation of partial computable functions)

۸- تابع جهانی (Universal function)

۴- مجموعه‌های ‌نمایه (Index sets).

۹- تابع جهانی رایانش‌پذیر نیست.

۵- مجموعه نمایه بدیهی و نابدیهی (Trivial and non-trivial index set).

■ مقدمه

در این قسمت از سلسله یادداشت‌های نظریه رایانش، مفهوم رایانش‌پذیری (بازگشتی) را به رایانش‌پذیری جزئی (بازگشتی جزئی) گسترش خواهیم داد. سرانجام تابع جهانی (نیز ماشین جهانی) را معرفی خواهیم کرد.

در یاداشت ماشین‌های اندوختگانی، مثال ۹.۱، ماشینی را مشاهده کردیم که مدل برای یک تابع جزئی سره، یعنی تابع زیر است:

div(x, y) =
[x] اگر y > 0:
↑ اگر y = 0:

این ماشین، که نمودار آن را می‌توان در مثال ۹.۱ در بحث ماشین‌های اندوختگانی دید، برای مقادیر دامنه تابع div، مقدار تابع را رایانش و اجرای آن پایان می‌پذیرد↝. در غیر این صورت، یعنی برای ورودی‌های بیرون از دامنه آن در حالت تعلیق دائمی خواهد ماند.

آنچه از این مثال به دست می‌آید اینکه ماشین‌های اندوختگانی، به عنوان مدل، فراتر از توابع رایانش‌پذیر (کامل) هستند. از این جهت و نیز آنچه بیشتر خواهیم دید، مفهوم رایانش‌پذیری جزئی (بازگشتی جزئی) به میان خواهد آمد.

■ یادآور

☚: در این قسمت، همه نگاشت‌ها [توابع (کامل) و توابع جزئی]، مگر خلاف آن گفته شده باشد، از مجموعه توانی اعداد طبیعی، یعنی ℕn برای n≥۱، در ℕ تعریف می‌شوند. برای مثال:

f۱ : ℕ۲ → ℕ: f(x۱, x۲) = ۲x۱ + x۲ + ۱.

و به طور کلی:

f(x) : ℕn → ℕ.

☚: مراد از x (یا x<..,k>) دنباله متغیرهای (x۱,...,xk) برای k≥۱ است. برای مثال دنباله متغیرهای (x۱,x۲,x۳).

☚: فرض کنید A و R به ترتیب کلاس و رابطه باشند. ~A و ~R (همچنین A و R) به ترتیب عبارت‌اند از:

~A = A ⇔ {x|x ∉ A} (کلاس متمم)

~R = R ⇔ ~R(x)

■ توابع بازگشتی جزئی (Parial recursive function - μrc)

تابع f(x) یک تابع بازگشتی جزئی [نیز تابع رایانش‌پذیر جزئی - نیز تابع μ-بازگشتی (μ-recursive functions) با کوته نام μRc] است اگر دنباله متناهی توابع جزئی:

F۱, . . . , Fi, . . ., Fn

وجود داشته باشد، به قسمی که:

F = Fn

و برای ۱≤ k ≤ n

۱.تابع Fk یک تابع نخستینی باشد، یا

۲. برای ۱< kتابع Fk توسط قاعده ترکیب (R۱) از میان توابع F۱ تا Fk-۱ به دست آمده باشد. یا

۳. برای ۱≤ k تابع Fk توسط قاعده بازگشتی نخستینی (R۲) از توابع F۱ تا Fk-۱ به دست آمده باشد، یا

۴. برای ۱< kتابع Fn توسط کمینه سازی بیکران از میان توابع F۱ تا Fk-۱ به دست آمده باشد.

[تعریف برهان را در اینجا ببینید.]

☚: بنابر تعریفِ تابع بازگشتی، هر تابع بازگشتی یک تابع بازگشتی جزئی نیز است↝. در ادامه نشان خواهیم ‌داد تابعی هست که بازگشتی-جزئی است اما بازگشی نیست. بنابراین و بنا به تز چرج-تورینگ:

بازگشتی جزئی ⊂ بازگشتی ⊂ بازگشتی نخستینی

⇕

رایانش‌پذیر جزئی ⊂ رایانش‌پذیر ⊂ رایانش‌پذیر نخستینی

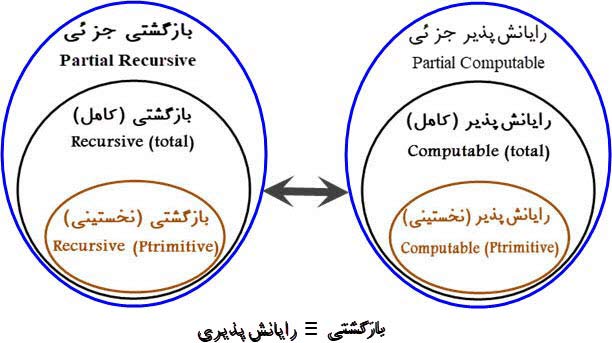
رایانش‌پذیری و ‌بازگشتی

☚: کلاس توابع بازگشتی جزئی را 𝓒μrc می‌نامیم.

کلاس توابع بازگشتی جزئی کوچک‌ترین کلاسی است که تحت اعمال بازگشتی نخستینی↝ و کمینه سازی بی‌کران بسته است (یعنی، حاصل انجام اعمال گفته شده روی اعضای 𝓒μrc در خود آن وجود دارند).

■ نمایه‌سازی توابع رایانش‌پذیر جزئی (Indexation of partial computable functions)

• قضیه صورت نرمال (Kleene Normal Form Theorem).

گیریم f(x) یک تابع k-گانه μrc باشد. در این صورت رابطه نخستینی-بازگشتی T(e,x,s)، تابع بازگشتی-نخستینی u(x) و اندیس e وجود دارند، به قسمی که:

f(x) ≃ u(μs(T(e, x, s))).

به رابطه نخستینی-بازگشتی T(e, x, s) در بالا، محمول T کلین (Kleene's T predicate) می‌گویند:

«اکنون T(i, a, x) را مطابق زیر در نظر بگیرید که در آن: i اندیس یک ماشین‌ تورینگ (که آن را "ماشین "Mi نامیده) باشد، به قسمی که و قتی برای a به عنوان یک آرگومان به کار زده شود، در لحظه x (اما نه پیش از آن) رایانش مقدار a را (که آن را "φi(a)") نامیده) به پایان رسانده باشد. استیون کول کلین↧»

Stephen Cole Kleene. Mathematical logic; Dover Publications (December 18, 2002). Pg. 243.

به عبارت دیگر، تابع search↝ و تابع u (که هر دو p.r هستند) وجود دارند، به قسمی که:

search(x) ≃ μs(T(e, x, s))

و

f(x) ≃ u(search(x).

در تعبیر (مدل رایانشی) می‌گوییم، از آنجا که T رایانش‌پذیر است می‌توان تابع search↝ را در s گام در اجرای برنامه e↝ برآورد و نتیجه را در ورودی تابع u که نیز رایانش پذیر است قرار داد و مقدار تابع u، به ازای این ورودی را، که مقدار f با ورودی x است، به دست آورد. حاصل این روند φe(x) ‌است. اکنون e را اندیس (Index) تابع f می‌نامیم و می‌نویسیم:

f(x) ≃ φe(x).

بنابراین، به هر تابع μrc یک عدد طبیعی، به فرض e، نظیر می‌گردد و نیز برعکس آن. این یعنی، توابع رایانش‌پذیر جزئی (μrc) را می‌توان نمایه سازی (فهرست) کرد (آنها را برشمرد). به عبارت دیگر، داریم:

کلاس نمایه‌سازی توابع بازگشتی جزئی k-گانه

↓

𝓒k-μrc = {φ۰(x), φ۱(x), ..., φi(x), ...}

که در آن رابطه زیر برای اعضای آن برقرار است:

φi(x) ≃ μs (Tk(i, x, s)).

[μs (T(i, x, s)) وقتی k مشخص است فقط می‌نویسیم:]

☚: برای تابع φe به ازای ورودی x رابطه رایانش‌پذیر-نخستینی:

T(e, x, s)

وجود دارد.

☚: مجموعه اندیس‌های اعضای 𝓒k-μrc را Ik-μrc می‌نامیم.

☚: مجموعه اندیس‌های اعضای 𝓒μrc↜ را Iμrc می‌نامیم (Ik-μrc⊂Iμrc).

در هر مدل رایانشی، بنا به آنچه گفته شد، به هر تابع (یا برنامه) می‌توان یک نام یکتا نظیر کرد↝. از سوی دیگر، توجه داریم که به هر تابع (یا برنامه) می‌توان به هر تعداد دستورات غیرموثر، برای نمونه دستور زیر

for (int i = 0; i < 1; i++) {}

را به انتهای برنامه افزود. بنابراین به ازای تابعی با نام «e» در مدل رایانشی معین نامتناهی تابع هم‌ارز وجود دارد. به عبارت دیگر، در نمایه‌سازی بالا برای هر اندیس e تعداد نامحدود (زیر)اندیس e وجود دارد. در اینجا و در ادامه ما e را نماینده همه‌ این (زیر)اندیس‌ها (کدها / برنامه‌ها) در یک مدل رایانش معین فرض می‌کنیم.

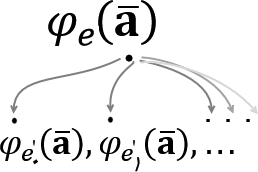
نمایه سازیی توابع بازگشتی جزئی

☚: نتیجه. قضیه برشمارش

برای هر تابع رایانش‌پذیر جزئی f اندیس e وجود دارد، به قسمی که:

 f(x) ≃ φe(x)

که در آن:

e∈Iμrc; φe(x) ∈ 𝓒μrc.

☚: تابع جزئی f، آن گونه که در زیر تعریف شده است، یک تابع بازگشتی جزئی است.

f(x) =
۰ f(x)↑ اگر
۱ وگرنه

زیرا داریم:

f(x) ≃ φe(x) = ۰ × μs(T(e, x, s)) + ۱.

[در رابطه بالا اگر T(e,x,s) نامعین باشد عبارت سمت را آن نامعین خواهد بود.]

☚: تابع udf (با دامنه تهی↝)، که در زیر آمده است، یک تابع بازگشتی جزئی است.

udf(x) =
udf(x)↑

■ مجموعه‌های ‌نمایه (Index sets).

تعریف. مجموعه نمایه: فرض کنید C⊆𝓒μrc↜ باشد. آنگاه به مجموعه IC تعریف شده در زیر:

IC = {i: φ(i) ∈ C}

مجموعه نمایه C می‌گویند اگر  IC دارای ویژگی زیر:

[(j∈IC) ∧ (φj(x) ≃ φr(x))] ⇒ r∈IC

باشد. بنابراین، مجموعه‌های Iμrc↜=N و I∅=∅ مجموعه نمایه هستند.

■ مجموعه نمایه بدیهی و نابدیهی (Trivial and non-trivial index set).

به یک مجموعه نمایه، به فرض I، یک مجموعه نمایه نابدیهی (non-trivial index set) گفته می‌شود اگر اعضای آن همه آن ویژگی‌هایی را که توسط همه توابع بازگشتی برآورده می‌شوند را نداشته باشند (به عبارت دیگر I دارای یک ویژگی نابدیهی باشد). برای مثال مجموعه نمایه توابع r.c یک مجموعه نمایه نابدیهی است. همچنین، مجموعه نمایه توابع μrc که در آن حداقل یک تابع r.c باشد و حداقل یک تابع r.c نباشد یک مجموعه نمایه نابدیهی است. در غیر این صورت به آن مجموعه نمایه بدیهی (trivial index set) می‌گویند. برای مثال مجموعه‌های:

 Iμrc=N، I∅↜=∅

و

 {e: φe = φe + ۱}

نابدیهی هستند.

■ تابع (جزئی) قطری (Diagonal partial function)

بنا به قضیه برشمارش تابع جزئی d در زیر (موسوم به تابع قطری):

 d(x) = φx(x) + ۱

که در آن:

Dom(d) = {φx(x)↓}

یک تابع μrc است.

از آنجا که d یک تابع μrc است بنا به قضیه برشمارش اندیس e وجود دارد به قسمی که:

(d): d(x) = φx(x) + ۱ ≃ φe(x)

[توجه داشته باشید در (d): x متغیر و e یک اندیس معین است که می‌دانیم وجود دارد.]

اگر در (d) مقدار x را اندیس e قرار دهیم، داریم:

 φe(e) + ۱ ≃ φe(e).

☚: از تابع قطری در ادامه و پس از معرفی مجموعه نمایه قطری  در اثبات تصمیم‌ناپذیری بهره خواهیم برد.

■ روش قطری در اثبات وجود تابع کامل رایانش‌نا‌پذیر.

می‌خواهیم نشان دهیم تابعی یک متغیری وجود دارد که رایانش‌پذیر نیست و برای این کار از روش قطری↝ استفاده می‌کنیم. از آنجا که کلاس توابع رایانش‌ پذیر زیر-کلاس μrc است، پس می‌توان آنها را برشمرد. در زیر این برشمارش آمده است:

θ۰, θ۱, . . ., θx-۱, θx, θx+۱, . . .

نیز در ماتریس پایین (با تعداد سطر و ستون نامتناهی) برشمارش بالا همراه با برشمارش مقادیر متغیر x نشان داده شده است:

برشمارش توابع رایانش‌پذیر یک متغیری
i→
↓		۰۱...i-۱ii+۱...
θ۰θ۰(۰)θ۰(۱)...θ۰(i-۱)θ۰(i)θ۰(i+۱)...
θ۱θ۱(۰)θ۱(۱)...θ۱(i-۱)θ۱(i)θ۱(i+۱)...
.
.
.		.
.
.		.
.
.		.
.
.		  .
.
.		.
.
.		.
.
.
θi-۱θi-۱(۰)θi-۱(۱) θi-۱(i-۱)θi-۱(i)θi-۱(i+۱)...
θiθi(۰)θi(۱)...θi(i-۱)θi(i)θi(i+۱)...
θi+۱θi+۱(۰)θi+۱(۱)...θi+۱(i-۱)θi+۱(i)θi+۱(i+۱)...
.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.

در زیر دنباله عناصر قطر ماتریس آمده است:

θ۰(۰), θ۱(۱), . . ., θn(n), . . .

ما (در روش قطری) در پی ساختن تابع f(n) از عناصر دنباله قطری در بالا خواهیم بود، یعنی دنباله:

f(۰), f(۱), . . ., f(n), . . .

به قسمی که برای هر n داسته باشیم f(n) ≠ θn(n). این تابع، یعنی f(n)، را به گونه زیر تعریف می‌کنیم:

f(n) =
θn(n) + ۱اگر θn(n)↓:
۰اگر θn(n)↑:

آشکار است که f کامل است.

 بنابراین:

اگر θn(n)↓، یعنی θn در n معین باشد، آنگاه متفاوت از f(n) است، در غیر این صورت، یعنی وقتی θn(n) نامعین است، مقدار f(n) صفر است.  

از آنجا که تابع کامل f متفاوت از θx است پس در برشمارش توابع رایانش‌پذیر وجود ندارد و در نتیجه رایانش‌پذیر‌ نیست.

■ تابع جهانی (Universal function)

تابع و ماشین جهانی / Universal Function and machine

در این بند تابعی رایانش‌پذیر جزئی موسوم به تابع جهانی را معرفی می‌کنیم که دربردار همه توابع کلاس μrc است. بنابراین، متناظر با تابع جهانی می‌توان از ماشین اندوختگانی جهانی↝ به عنوان مدل رایانشی آن نام برد.

تعریف. گیریم f یک تابع k متغیری رایانش‌پذیر جزئی باشد. آنگاه به تابع k+۱ متغیری Uk-univ(e,x)، که به گونه زیر تعریف شده است:

Uk-univ(e, x) ≃ f(x).

تابع جهانی گفته می‌شود.

قضیه. برای هر k تابع جهانی Uk-univ(e, x)، که رایانش‌پذیر جزئی است، وجود دارد. (اثبات:↧)

Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, 1980. P.86.

بنابراین، می‌توان نوشت:

Uk-univ(e, x) ≃ f(x). [f(x) ≃ φe(x)∈𝓒μrc↜]

همانطور که می‌توان دید متغیر اول ورودی تابع κk-univ، یعنی e، شناسه (اندیس) یک تابع (اختیاری، نیز ماشین اندوختگانی یا یک برنامه به زبان C و مانند آن) رایانش‌پذیر جزئی (در اینجا f) است و متغیر دوم ورودی آن متغیر ورودی تابع f، یعنی x، است. بنابراین تابع جهانی دربردار همه توابع رایانش‌‌پذیر (و رایانش‌پذیر جزئی) است.

به عبارت دیگر، یک ماشین اندوختگانی (یا برنامه P) وجود دارد که از عهده اجرا (رایانش) تابع جهانی برمی‌آید و دربردار همه برنامه‌های دیگر نیز است و از این جهت است که به آن برنامه جهانی (نیز ماشین جهانی) می‌گویند. اما، نکته مهمی نیز هست که در بند بعدی می‌آید و آن این که گرچه تابع جهانی رایانش‌پذیر جزئی است، اما رایانش‌پذیر نیست.

■ تابع جهانی [Uk-univ(i, x)] رایانش‌پذیر نیست.

با بهره گیری از روش برهان قطری می‌توان نشان داد تابع جهانی اگرچه یک تابع رایانش‌پذیر جزئی است ولی رایانش‌پذیر نیست. بنابراین کلاس توابع رایانش‌پذیر زیرکلاس سره توابع رایانش‌پذیر جزئی است. یعنی تابعی وجود دارد که رایانش‌پذیر جزئی است و رایانش‌پذیر (کامل) نیست.

در اینجا مرور ما در بحث توابع بازگشتی جزئی پایان می‌یابد. در یادداشت‌ بعد در پی مفهوم نیمه-تصمیم‌پذیری (semi-decidability) و پرسش‌های مربوط به آن خواهیم بود.

منابع و ارجاعات

1- Davis, Martin, editor. The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.

این کتاب مجموعه‌ای از مقالات بنیادی در درباره (مسئله) تصمیم ناپذیری و حل ناشدنی است. که توسط مارتین دیویس ویرایش شده است. کتاب با مقاله برجسته گودل در سال ۱۹۳۱ (قضیه ناتمامیت) آغاز می‌شود. ویرایشگر کتاب مارتین دیویس (۲۰۲۳ - ۱۹۲۸) یک منطقدان، ریاضیدان و دانشمند کامپیوتر آمریکایی است. وی سهم قابل توجهی در زمینه‌های نظریه رایانش و منطق ریاضی داشت. او بیشتر به خاطر کارش روی پرسش دهم هیلبرت که منجر به قضیه MRDP می‌گردد، شناخته شده است.

i. <https://www.logicmatters.net/resources/pdfs/MRDP.pdf>
ii. <http://www.scholarpedia.org/article/Matiyasevich_theorem>

2- Davis, Martin. The Universal Computer: The Road from Leibniz to Turing. CRC Press/Taylor & Francis Group, 2018.

3- Davis, Martin,  Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.

4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf

5- Stephen Cole Kleene. Mathematical logic, Dover Publications (December 18, 2002).

6- Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, (1980.)

7- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.

8- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing.  (2011).

9- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)

10- George Tourlakis, Computability, Springer International Publishing. (2022.)

11- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. (2015.)

12- Hartley Rogers, Jr· Theory of Recursive Functions and Effective Computability. The MIT Press; Fifth Printing edition (April 22, 1987).

13- Herbert B. Enderton An Introduction to Recursion Theory. Academic Press is an imprint of Elsevier (2011).

14. Dean, Walter, "Recursive Functions", The Stanford Encyclopedia of Philosophy (Winter 2021 Edition), Edward N. Zalta (ed.)

◄ توجه: