≡
فهرست:
نظریه رایانش - تصمیم‌پذیری - نیمی-تصمیم‌پذیر درآمدی یه منطق

تصمیم‌پذیر، نیمی-تصمیم‌پذیر و روش کاهش در حل مسئله

منطق و نظریه رایانش (۵)

درآمد به منطق

در قسمت پیشین با مفهوم رایانش‌پذیری جزئی (برای توابع) روبرو شدیم. در این قسمت این گونه جزئیت را برای مجموعه نیز گسترش خواهیم داد. به عبارت دیگر، این قسمت با سخن از مسئله‌های نیمه قابل حل (نیمی-تصمیم‌پذیر) آغاز خواهد شد. اگرچه و در واقع این مسئله‌ها حل‌شدنی نیستند، اما حداقل می‌توان مورد‌های این مسئله‌ها (نیمی-تصمیم‌پذیر) را بطور مکانیکی برشمرد. در ادامه این قسمت نمونه‌های مشهوری از مسئله‌های حل نشدنی و اثبات حل ناشدنی آن‌ها را با استفاده از روش قطری خواهیم دید. سپس روش کاهش (Reduction method) را به عنوان دومین روش در اثبات حل ناشدنی معرفی خواهیم کرد.

روند منطق و نظریه رایانش (۵): تصمیم‌پذیر، نیمی-تصمیم‌پذیر و روش کاهش در حل مسئله

≡

۱- مقدمه (تصمیم‌پذیر و نیمی تصمیم‌پذیر).

۸- مسئله توقف رایانش‌پذیر نیست.

۲- رابطه‌های رایانش‌پذیر برشمردنی (Computably Enumerable Relations).

۹- مجموعه توقف قطری (Diagonal halting set).

۳- مجموعه‌های رایانش‌پذیر برشمردنی (Computably Enumerable).

۱۰- مجموعه توقف قطری (K) تصمیم‌پذیر نیست.

۴- برخی ویژگی در باره مجموعه‌های رایانش‌پذیر برشمردنی.

۱۱- نمایه توابع کامل رایانش‌پذیر برشمردنی (c.e) نیست.

۵- قضیه متمم (Complementation Theorem).

۱۲- رایانش‌پذیری نسبی، درجه سختی و روش کاهش در اثبات حل‌شدنی و حل نا‌نشدنی مسئله.

۶- مجموعه توقف (K⚬).

۱۳- کارزدن روش کاهش در اثبات تصمیم ناپذیری.

۷- مسئله توقف.

۱۴- مجموعه کامل (چند-یک) - (m-Complete set).

■ مقدمه (تصمیم‌پذیر و نیمی تصمیم‌پذیر)

 متناظر با آنچه برای رایانش‌پذیری جزئی گفته شد را می‌توان برای مجموعه‌ها نیز گفت. [برای یاد آوری تابع f رایانش‌پذیر جزئی است اگر ۱- برای هر x ∈ Dom(f) ماشین اندوختگانی متناظر آن با مقدار صحیح f(x) پایان یابد↝. ۲- برای هر x ∉ Dom(f) ماشین اندوختگانی متناظر آن پایان ناپذیر باشد.]

فرض کنید 𝓤 و S دو مجموعه باشند و داشته باشیم S⊆𝓤.

(آ)- اگر برای هر x ∈ 𝓤 تابع مشخصه S، یعنی χS، رایانش پذیر (کامل) باشد، آنگاه می‌گوییم S در 𝓤 تصمیم‌پذیر↝ است.

(ب)- اگر برای هر x ∈ S تابع مشخصه S، یعنی χS، رایانش پذیر (کامل) باشد، آنگاه می‌گوییم S برای 𝓤 نیمی-تصمیم‌پذیر↝ است.

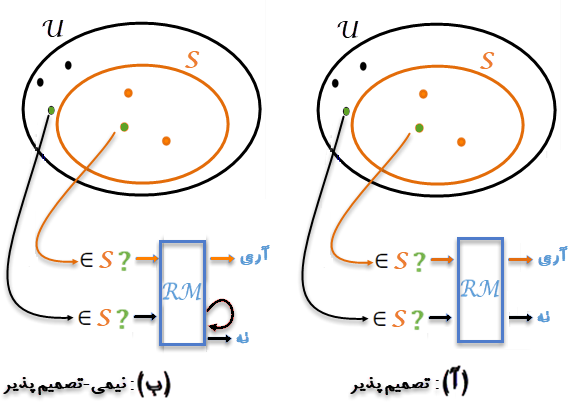
تصمیم پذیری و نیمی-تصمیم‌پذیری
شکل. ۱. تصمیم‌پذیری و نیمی-تصمیم‌پذیری↝.

در حالت (ب) اگر چه رایانش عضوی مانند x در 𝓤 برای x∈S تصمیم‌پذیر است، یعنی S برای خود یک مجموعه تصمیم‌پذیر است، اما برای x∈𝓤? می‌تواند تصمیم‌ناپذیر (نامعین) باشد.

به ماشین‌ اندوختگانی حالت (ب)، یعنی یک ماشین نیمه-تصمیم‌پذیر، گفته می‌شود صرفاً شناسنده (Recognizer) عناصر S است. چنین ماشینی برای عناصر غیر S می‌تواند به حالت تعلیق دائم در آید.

به ماشین‌ اندوختگانی حالت (آ)، یعنی تصمیم‌پذیر، گفته می‌شود افزون بر شناسندگی عناصر S پذیرنده (Acceptor) عناصر S نیز هستند. چنین ماشینی برای عناصر S و غیر S همیشه با پاسخ آری / نه پایان می‌یاید.

توجه داشته باشید مطابق آنچه گفته شد، یک مجموعه تصمیم‌پذیر نیمی-تصمیم‌پذیر هم است ولی وارون آن می‌‌تواند برقرار نباشد. در ادامه این قسمت ابتدا به مجموعه‌های رایانش‌پذیرِ برشمردنی می‌پردازیم. یعنی مجموعه‌هایی که اعضای آن‌ها به صورت بازگشتی قابل شمارش هستند، اگرچه ممکن است قابل تصمیم‌گیری نباشند. به عبارت دیگر، مفهوم قابل شمارش بودن اعضای یک مجموعه بگونه یک روند مکانیکی بازگویی می‌کنیم. سپس خواهیم دید مجموعه رایانش‌پذیرِ برشمردنی و مجموعه نیمه-تصمیم‌پذیر دو مفهوم با مصادیق یکسان هستند.

☚: به مسئله‌هایی که تصمیم پذیر نیستند (مسئله) تصمیم ناپذیر گفته می‌شود. بنابراین یک مسئله‌ تصمیم ناپذیر می‌تواند نیمی-تصمیم‌پذیر باشد، ولی نمی‌تواند تصمیم پذیر باشد.

■ یادآور

☚: در این قسمت، همه نگاشت‌ها [توابع (کامل) و توابع جزئی]، مگر خلاف آن گفته شده باشد، از مجموعه توانی اعداد طبیعی، یعنی ℕn برای n≥۱، در ℕ تعریف می‌شوند. برای مثال:

f۱ : ℕ۲ → ℕ: f(x۱, x۲) = ۲x۱ + x۲ + ۱.

و به طور کلی:

f(x) : ℕn → ℕ.

☚: مراد از x (یا x<..,k>) دنباله متغیرهای (x۱,...,xk) برای k≥۱ است. برای مثال دنباله متغیرهای (x۱,x۲,x۳).

☚: فرض کنید A و R به ترتیب کلاس و رابطه باشند. ~A و ~R (همچنین A و R) به ترتیب عبارت‌اند از:

~A = A ⇔ {x|x ∉ A} (کلاس متمم)

~R = R ⇔ ~R(x)

• معرفی نماد ≃:

گیریم f و g دو تابع باشند. می‌نویسیم:

f ≃ g

اگر برای هر x داشته باشیم f و g هر دو معین با مقدار مساوی باشند یا هر دو معین نباشند. به عبارت دیگر:

g(x) ≃ f(x)↓ ⇔ (f (x)↑ ∧ g(x)↑) ⋁ ∃z(f (x) = z ∧ g(x) = z).

نیز گیریم Q و R رابطه‌های nتایی باشند. گوییم:

R ≃ Q

اگر برای هر x رابطه‌های R و Q هردو رایانش‌پذیر باشند یا هردو رایانش‌پذیر نباشند.

■ رابطه‌ رایانش‌پذیر برشمردنی (Computably Enumerable Relation)

گیریم R(x) یک رابطه nگانه باشد، آنگاه R را یک رابطه رایانش‌پذیر برشمردنی (نیز رابطه بازگشتی برشمردنی - Recursively Enumerable sets) گوییم اگر رابطه n+۱گانه و رایانش‌پذیر Q باشد به قسمی که:

R(x) ⇔ ∃b Q(x, b).↜

☚: هر رابطه بازگشتی یک رابطه بازگشتی برشمردنی است.

اثبات: گیریم R(x) یک رابطه بازگشتی nگانه باشد، اکنون بناشده بر R رابطه n+۱گانه Q را تعریف می‌کنیم به قسمی که:

R(x) ⇔ Q(x, xn+۱).

از آنجا که R رایانش‌پذیر است پس ∃bQ(x, b).

■ مجموعه‌های رایانش‌پذیر برشمردنی - Computably Enumerable (c.e).

گیریم A یک مجموعه باشد، A را یک مجموعه رایانش‌پذیر برشمردنی (نیز مجموعه بازگشتی برشمردنی)، با کوته نام c.e، گوییم اگر تهی باشد یا اعضای آن برد یک تابع رایانش‌پذیر باشند.

به عبارت دیگر: مجموعه A رایانش‌پذیر برشمردنی است اگر:

A=∅

یا

A= Rng(f)={m: ∃n; f(n)↓= m; یک تابع رایانش‌پذیر f(n)}

[به عبارت دیگر، مجموعه‌های رایانش‌پذیر برشمردنی بگونه بازگشی (r.c) برشمرده می‌شوند.]

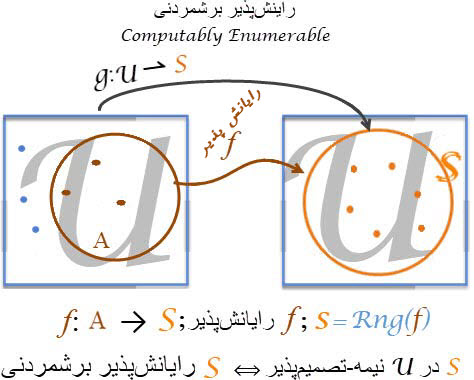
رایانش‌پذیر برشمردنی - Computably Enumerable
شکل. ۲

همانطور که در شکل ۲ می‌توان دید، یک مجموعه رایانش‌پذیر-برشمردنی مانندS گرچه برای خود تصمیم‌پذیر است اما برای 𝓤 نیمه-تصمیم‌پذیر باشد. همین‌طور، یک مجموعه نیمه‌-تصمیم‌پذیر مانند S (یعنی مجموعه‌ای که برای خود تصمیم‌پذیر است) به موجب وجود تابعی رایانش‌پذیر (f در ش.۲) برشمردنی هم هست.

برای مثال مجموعه اعداد زوج رایانش‌پذیر برشمردنی است، زیرا داریم:

f(n) = mul(S(S(Z(n))), n).

Rng(f) = {۰, ۲, ۴, . . .}

☚: مجموعه‌های رایانش‌پذیر، رایانش‌پذیر برشمردنی نیز هستند.

فرض کنید مجموعه A رایانش‌پذیر باشد. پس A یا تهی است که طبق تعریف رایانش‌پذیر برشمردنی است. اگر A≠∅ پس a به قسمی که a∈A وجود دارد. اکنون تابع f با برد A را به شیوه زیر تعریف می‌کنیم:

f(x) =
xاگر χA(x) = ۱
aوگر نه [یعنی χA(x) = ⚬]

روشن است که تابع f رایانش‌پذیر↝ است و برد آن مجموعه A است. پس A رایانش‌پذیر برشمردنی است↝.

■ برخی ویژگی در باره مجموعه‌های رایانش‌پذیر برشمردنی.

اگر A ⊆ ℕ آنگاه داریم↧:

Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, 1980. P.124.

A رایانش‌پذیر برشمردنی است.

⇓

۱: A = ∅ یا A برد یک تابع p.r. است.

⇓

A = {n ∈ ℕ: ∃yR(n, y)} - بازگشتی R :۲

⇓

۳: A دامنه یک تابع یک متغیری r.c. است.

⇓

A رایانش‌پذیر برشمردنی است.

☚: بنا به ۳ دربالا، اگر A یک c.e. باشد آنگاه یک تابع رایانش‌پذیر، به فرض f، هست که A دامنه آن است. بنابراین، بنا به نمایه‌سازی توابع μrc باید اندیس n باشد، به قسمی که:

φn(x)↓ = f(x).

از اینجا مجموعه Wn در زیر وجود دارد:

Wn = Dom(φn) = {x:φn(x)↓}.

بنابراین:

x∈Wx ⇔ φx(x)↓ ⇔ RM<x, x>↓ ⇔ U۱-univ(x, x)↓

Wn = {x: φn(x)↓} ⇒ Wx = {x: φx(x)↓}.

پس دنباله:

W⚬ , W۱ , W۲ , . . .

یک برشمارش همه مجموعه‌های c.e. است. به عبارت دیگر، اگر A یک c.e باشد آنگاه اندیس e هست، به قسمی که:

A = We .

مجموعه‌های برشمارشی بازگشتی(نظریه رایانش پذیری)

برای نمونه، مجموعه‌های اعداد زوج (f(n)=۲n) و نیز {۵} [با تکرار] وقتی f(n)=Cte(۵) باشد برشمردنی هستند.

همچنین، اگر A و B دو مجموعه c.e باشند آنگاه Wi و Wj هستند که:

A = Wi و B = Wj,

بنابراین می‌توان نوشت:

A ∪ B = Wi∪j; A ∩ B = Wi∩j .

☚: همچنین می‌توان Wkn را بگونه زیر تعریف کرد:

Wkn = {x۱,...,xk: φn(x۱,...,xk)↓}.

اما همیشه می‌توان از شمارگذاری گودل برای برای کد کردن (و وارون آن) سود جست. از این جهت (در نظریه رانش‌پذیری) چنین مجموعه‌هایی متناظر با مجموعه‌های Wn هستند و نیاز نیست آنها را جداگانه در نظر گرفت.

☚: فرض کنید R(x, y) یک رابطه c.e. باشد. در این صورت مجموعه:

{x: ∃yR(x, y)}.

 c.e. است. بنابراین، گیریم رابطه:

R(x, y۱, . . . ,yn)

c.e. باشد. آنگاه مجموعه:

{x: ∃y۱, . . . ,∃yn R(x, y۱, . . . ,yn)}

 زیر نیز c.e. است.

■ قضیه متمم (Complementation Theorem)

A تصمیم‌پذیر است اگر و تنها اگر خود و متمم آن، یعنی ~A، ‌نیمه-تصمیم‌پذیر باشند.

اثبات:

آ- فرض می‌کنیم A تصمیم‌پذیر باشد. پس ~A↝ هم تصمیم‌پذیر خواهد بود. اما، هر تصمیم‌پذیر نیمی-تصمیم‌پذیر هم است↝.

ب- فرض می‌کنیم A و ~A نیمی-تصمیم‌پذیر باشند. نیز فرض کنید RMa یک ماشین‌ اندوختگانی باشد که A دامنه ورودی‌های آن باشد. همچنین فرض کنید RMb ماشین‌ اندوختگانی باشد که ~A دامنه ورودی‌های آن باشد. الگوریتم زیر نشان می‌دهد عضویت x در A تصمیم‌پذیر است.

۱- دو ماشین RMa و RMb را برای ورودی x به‌طور همزمان آغاز ‌کنید.

۲- اگر ماشین RMa پایان یاید آنگاه x∈A.

۳- اگر ماشین RMb پایان یاید آنگاه x∈~A.

صحت الگوریتم: از آنجا که، x∈A یا x∈~A پس اجرای یکی از این دو ماشین پایان می‌یابد.

به عبارت دیگر اگر A و ~A نیمی-تصمیم‌پذیر باشند آنگاه رابطه‌های تصمیم‌پذیر پذیر R و S هست به قسمی‌که:

x ∈ A ⇔ ∃yR(x, y);
x ∈ ~A ⇔ ∃yS(x, y).

قطعه کد زیر نشان ‌می‌دهد A تصمیم‌پذیر است:

for (y : 0 → ∞)
{
if R(x, y) {write ("yes"); exit}
if ; S(x, y) {write ("No"); exit}
}

■ مجموعه توقف (K⚬).

مجموعه K⚬ که در زیر تعریف شده است به مجموعه توقف موسوم است:

K⚬ = {i: φi(x)↓} = {i: ∃x∃yT(i, x, y)↜}

= {<i, x>:φi(x)↓} ⊂ ℕ×N.

K⚬ تصمیم‌پذیر است اگر تابع مشخصه آن h به قرار:

h(x, y) = χk⚬.(<x, y>)

یک تابع رایانش‌پذیر‌↝ باشد.

☚: در بند بعد (مسئله توقف) نشان می‌دهیم h(x,y) رایانش‌پذیر نیست.

مسئله توقف (تصمیم پذیری) - K⚬
i
↓		x→۰۱. . .i. . .
۰ φ۰(۰)↓? φ۰(۱)↓?. . . φ۰(i)↓?. . .
.
.
.		.
.
.		.
.
.		. . ..
.
.		 .
.
.
i φi(۰)↓? φi(۱)↓? . . . φi(i)↓? . . .
.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.

■ مسئله توقف.

گزاره زیر در منطق (نظریه رایانش) به مسئله توقف (نیز مسئله‌ تصمیم‌پذیری) مشهور است.

«ماشین اندوختگانی (یا ماشین تورینگ) با شناسه i برای ورودی x پایان‌پذیر است.» به عبارت دیگر، آیا ماشین اندوختگانی (یا ماشین تورینگی) هست که در باره پایان‌پذیر بودن یک ماشین اندوختگانی (یا ماشین تورینگی) از جمله خودش، تصمیم‌ آری / نه بگیرد؟ [آیا K⚬ تصمیم‌پذیر است؟]

به عبارت دیگر، برخی ماشین‌های اندوختگانی (یا ماشین‌های تورینگ و مانند آنها) ممکن است درگیر محاسباتی شوند که برای همه ورودی‌ها متوقف نشوند. و از اینجا، اگر چه هر الگوریتم را می‌توان توسط یک ماشین اندوختگانی (یا ماشین‌های تورینگ و مانند آن) پیاده سازی کرد، هر ماشین اندوختگانی (یا ماشین‌های تورینگ و مانند آن)  لزوماً با یک الگوریتم مطابقت ندارد.

مسئه توقف

پاسخ به پرسش بالا (مسئله توقف) منفی است. چند خط پایین‌تر نشان می‌دهیم چنین ماشینی خودویرانگر است، یعنی فرض وجود آن مستلزم وجود نداشتن آن است. مسئله تصمیم‌ ناپذیری (مسئله توقف‌ناپذیری)، به گونه‌ای یادآور قضیه‌های ناتمامیت گدل هستند. در واقع گونه ضعیفی از قضیه اول ناتمامیت از مسئله توقف قابل استنتاج است.↧

George Tourlakis. (2022). Computability, Springer International Publishing. Gödel’s First Incompleteness Theorem via the Halting Problem. ch 8..

■ مسئله توقف رایانش‌پذیر نیست.

اثبات:

فرض می‌کنیم تابع مشخصه مجموعه توقف، یعنی h(x۱,x۲)، رایانش‌پذیر باشد (برهان غیرمستقیم). بنابراین، تابع g(x) که در زیر تعریف شده است رایانش‌پذیر جزئی است (چون تابع h بنا بر فرض رایانش‌پذیر است):

g(𝓍) =
۰اگر h(x۱,x۱)↓ = ۰:
↑ بی‌پایانوگر نه [یعنی h(x۱,x۱)↓ ≠ ۰]:

با توجه به نمایه‌سازی توابع رایانش‌پذیر جزئی اندیس j هست که:

I: g(𝓍) ≃ φj(𝓍).

اکنون فقط دو حالت متصور است:

۱- g(j)↓⇐بنابر تعریفِ g داریم: h(j, j)=۰ ⇐این یعنی φj(j)↑(بنابر I) ⇐g(j)↑
۲- g(j)↑⇐بنابر تعریفِ g داریم: h(j, j)≠۰. اما h تابع مشخصه HP است و به ناچار h(j, j)=۱.⇐این یعنی φj(j)↓(بنابر I) ⇐g(j)↓
خلاصه:اگر g(j)↓ آنگاه g(j)↑. (تناقض)
اگر g(j)↑ آنگاه g(j)↓. (تناقض)
نتیجه:

مسئله توقف رایانش‌ناپذیر نیست. به عبارت دیگر،

K⚬ = {<i, x>: φ(x)↓}

تصمیم‌پذیر نیست.

■ مجموعه توقف قطری (Diagonal halting set)

توقف قطری - K
i
↓		x→۰۱. . .i. . .
۰ φ۰(۰)↓? φ۰(۱). . . φ۰(i) . . .
۱ φ۱(۰) φ۱(۱)↓?. . . φ۱(i)
.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.
i φi(۰) φi(۱) . . . φi(i)↓? . . .
.
.
.		.
.
.		.
.
.		.
.
.		.
.
.		.
.
.

مجموعه K تعریف شده در زیر:

K = {x: x∈Dom(φx)} = {i: φi(i)↓} = Wx↜.

به مجموعه توقف قطری موسوم است.

■ مجموعه توقف قطری↝ (K) تصمیم‌پذیر نیست.

در این بند (از دو راه) با استفاده از روش قطری نشان می‌دهیم K تصمیم‌پذیر نیست.

اثبات: روش قطری-۱:

(فرض خلاف): گیریم مجموعه توقف قطری↝، K در زیر، تصمیم‌پذیر باشد.

K = {i: φi(i)↓}

در این صورت تابع f، تعریف شده در زیر، μrc است.

f(x) =
↑بی‌پایانx ∈ Kاگر:
۰x ∉ Kاگر:

از آنجا که f یک تابع μrc است داریم f∈𝓒۱-μrc↝. بنابراین اندیس e هست به قسمی که:

f = φe.

در این صورت:

f (e)↓ ⇔ φe(e)↓

⇕

e ∈ K ⇔ f (e)↑ بی‌پایان.

بنابراین:

f (e)↓ ∧ f (e)↑.

که این یک تناقض است.

اثبات: روش قطری و قضیه متمم-۲:

یادآوری: در بند تعریف تابع جزئی قطری نشان دادیم برای تابع d(x) که μrc است داریم:

d(x) = φx(x) + ۱.

که در آن:

Dom(d) = {φx(x)↓} = K

(فرض خلاف): گیریم K تصمیم‌پذبر باشد. اکنون فرض کنید تابع رایانش‌پذیر f گسترش تابع d(x) باشد. بنابراین اندیس e هست به قسمی که:

f(e) = d(e) = φe(e) = φe(e) + ۱.

⇓

۱ = ۰

که این یک تناقض است. بنابراین تابع f (رایانش‌پذیر) وجود ندارد. اکنون تابع g در زیر را درنظر بگیرید:

g(x) =
d(x):x ∈ K اگر
۰:x ∉ Kاگر

تابع g گسترس تابع d است. اما بنا به آنچه دیدیم، تابع g رایانش پذیر نیست. بنابراین اگر K تصمیم‌پذیر (فرض خلاف) باشد آنگاه g می‌باید رایانش‌پذیر باشد. بنابراین K تصمیم‌پذیر نیست.

☚: از آنجا که K یک مجموعه c.e است ولی تصمیم‌پذیر نیست، پس بنا به آنچه در قضیه متمم آمده است K، یعنی:

K ={i: ∀xφi(x)↑}

c.e نیست. بنابراین مجموعه‌ای، K، هست که نه تنها تصمیم‌پذیر نیست بلکه نیمی-تصمیم‌پذیر هم نیست.

■ نمایه توابع کامل رایانش‌پذیر برشمردنی (c.e) نیست.

☚: نمایه توابع کامل با نام TOT شناخته می‌شود و تعریف آن به قرار زیر است:

TOT = {i: ∀x φi(x)↓}

اثبات به روش قطری.

فرض می‌کنیم (فرض خلاف) TOT رایانش‌پذیر برشمردنی (c.e) باشد. پس تابع رایانش‌پذیر f هست که TOT را برمی‌شمرد. یعنی، داریم:

TOT = {f(۰), f(۱), . . .}.

اکنون تابع h را بگونه زیر تعریف می‌‌کنیم:

h(x) = φf(x)(x) +۱.

آشکار است که h رایانش‌پذیر است. بنا به نمایه‌سازی ‌اندیس e هست، به قسمی که:

h(x) = φe(x). ∃i(e = f(i)).

اکنون می‌نویسیم:

h(i) = φf(i)(i) +۱= φe(i) + ۱ = h(i) + ۱;

که تناقض است.

اثبات با کارزدن تابع فراگیر↝.

فرض کنید C۱ کلاس توابع کامل یک متغیری باشد. می‌دانیم C۱ رایانش‌پذیر نیست. چرا که این مستلزم وجود تابع کامل یک متغیری است که رایانش‌پذیر نباشد↝. یعنی برای f(n)∈C۱ تابع کامل g(n)=f(n)+۱ وجود ‌دارد، به قسمی که: g(n)∉C۱.

اکنون فرض می‌کنیم (فرض خلاف) C۱ رایانش‌پذیر برشمردنی (c.e) باشد. پس تابع جهانی وجود دارد که این کلاس را بر‌می‌شمرد. بنابراین، در هر برشمارش توسط تابع فراگیر، توابع f و g هر دو برشمرده می‌شوند (حضور f همراه حضور g است). این یعنی داریم: g(n)∈C۱ که یک تناقض است. پس C۱ رایانش‌پذیر برشمردنی (c.e) نیست.

[به عبار دیگر:

بنا به فرض خلاف و بنا بر وجود تابع جهانی داریم:

∀i∃e: f(i) = U۱-univ(e, i)

و

∃e: g(n) = U1-univ(e, n)

و

g(n) ∉ C۱.

■  رایانش‌پذیری نسبی، درجه سختی و روش کاهش در اثبات حل‌شدنی و حل نا‌نشدنی مسئله

رایانش‌پذیری نسبی

"رایانش‌پذیری نسبی (Relative computability) در رابطه با پرسش از حل‌پذیری (رایانش‌پذیری) - یا حل‌ناپذیری - یک مسئله و قابل تحویل بودن (Reducibility) یا نبودن (کاهش‌پذیر بودن یا کاهش‌ناپذیر بودن) آن نسبت به مسئله دیگر است. امیل پست.↧"

Post, Emil L., “Recursively Enumerable Sets of Positive Integers and Their Decision Problems”, Bulletin of the American Mathematical Society, 1994, 50(5): p. 284–317.

به عبارت دیگر، اگر حل مسئله P۱ قابل کاهش به حل مسئله P۲ باشد، آنگاه راه حل P۲ بلافاصله پاسخ P۱ را به دست می‌دهد. حال آنکه، [وقتی P۱ به P۲ قابل کاهش است] اگر ثابت شود P۱ قابل حل نیست (رایانش‌ناپذیر نیست) آنگاه P۲ نیز قابل حل‌ نخواهد بود↝. در حالت اخیر می‌گوییم سختی حل‌ناپذیری P۱ بیشتر از سختی حل‌ناپذیری P۲ نیست. افزون بر این، اگر نیز ثابت شود حل‌ناپذیری P۲ کاهش‌پذیر به P۱ است گفته می‌شود درجه سختی حل‌ناپذیری P۱ و P۲ یکسان است. «پی‌گیری ما (در گسترش نظریه مجموعه‌های بازگشتی برشمردنی_ب.) عمدتاً بر این پرسش متمرکز است که آیا در بین این مسئله‌ها (تصمیم‌‌ناپذیر)، درجه حل‌ناپذیری کمتری از آنچه هست وجود دارد یا اینکه همه آنها (مسئله‌های تصمیم‌ناپذیر_ب.) به درجه یکسان حل‌ناپذیر هستند. امیل پست.↧» [همه مسئله‌های حل‌نا‌پذیر حل‌ناپذیر هستند، ولی بعضی بیشتر حل‌ناپذیر هستند↧؟]

Post, Emil L., “Recursively Enumerable Sets of Positive Integers and Their Decision Problems”, Bulletin of the American Mathematical Society, 1994, 50(5): p. 284–317.

https://studymind.co.uk/questions/all-animals-are-equal-but-some-are-more-equal-than-others-how-far-is-this-idea-important-in-animal-farm/.

گیریم P و Q دو مسئله تصمیم‌ گیری باشند، به قسمی که Q تصمیم‌پذیر باشد و هر دو در زبان از پیش معین ℒ قابل نوشتن (قابل بیان / expressible) باشند. نیز فرض کنید p مورد دلخواهی در P باشد. اکنون فرض کنید روند کارآمد r هست، به قسمی در آن تابع رایانش‌پذیر g مورد p در P را به مورد q در Q برمی‌گرداند. سپس تابع D (تصمیم‌ساز / Decider) در باره مورد q تصمیم‌گیری می‌کند (Q بنا به فرض تصمیم‌پذیر است و بنابراین خروجی تابع D پاسخ قطعی آری / نه است). در این حالت می‌گوییم P به Q کاهش پذیر است و می‌نویسیم:

P ≤m Q.

اندیس m بدین خاطر است که r می‌تواند چند به یک (many to one) باشد. اگر r یک به یک باشد آنگاه می‌نویسیم:

P ≤۱ Q.

نمودار زیر روند کاهش پذیری در حل مسئله
را آنگونه که توضیح داده شد نشان می‌دهد.
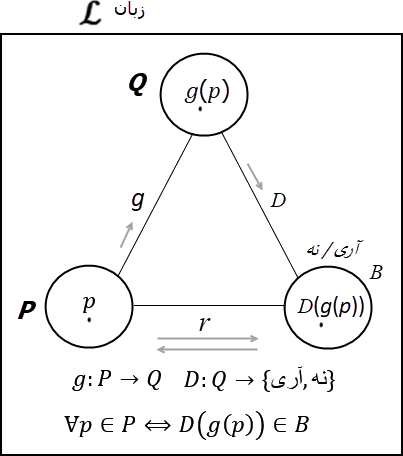
حل مسئله با استفاده از روش کاهش
شکل. ۳

p_مورد ∈ P ⟺ r(p_مورد) ∈ Q [برای هر مورد_p]:

با توجه به آنچه در باره نمایه‌سازی توابع و مجموعه‌های c.e گفته شد↝، می‌گوییم:

■ تعریف: کاهش‌پذیری (Reducibility)

گیریم A و B دو زیرمجموعه اعداد طبیعی باشند. گوییم A چند-یک (m-one reducible) کاهش‌پذیر به B است و می‌نویسیم:

A ≤m B

اگر تابع رایانش‌پذیر f باشد به قسمی که:

Mrd: ∀n ∈ ℕ: n ∈A ⟺ f(n) ∈ B.

به کاهش‌پذیری چند-یک کاهش‌پذیری نگاشتی (Mapping Reducibility) نیز گفته می‌شود.

☚: با توجه به تعریف کاهش‌پذیری داریم:

ℕ ≰m ∅.

■ گیریم:

P ≤m Q.

باتوجه به رابطه هم‌ارزی Mrd می‌گوییم:

آ.

۱. اگر Q تصمیم‌پذیر باشد آنگاه P نیز تصمیم‌پذیر است.

۲. اگر Q نیمی-تصمیم‌پذیر باشد آنگاه P نیز نیمی-تصمیم‌پذیر است.

ب.

اگر P تصمیم‌‌پذیر نباشد آنگاه Q نیز تصمیم‌نا‌‌پذیر است.↝

تعریف. هم‌ارزی چند.یک: (many-one equivalency).

گیریم P ≤m Q و Q ≤m P. در این حالت، می‌گوییم P و Q هم‌ارز چند-یک هستند و می‌نویسیم:

P ≡m Q .

آشکار است که ≡m بازتابی، ترایایی و متقارن است. بنابراین، ≡m یک رابطه هم‌ارزی است و مسئله تصمیم‌ گیری را به کلاس‌های هم‌ارزی افراز می‌کند.

درجه (تصمیم‌ناپذیری) چند-۱ (m-degree / many-one degree):

در بند رایانش‌پذیری نسبی از درجه تصمیم‌ناپذیری سخن گفتیم. اکنون آن را تعریف می‌کنیم.

تعریف: گیریم A یک مجموعه باشد. درجه چند-یک A (Many-one Degree) عبارت است از کلاس هم‌ارزی A نسبت به رابطه ≡m. بنابراین می‌نویسیم:

degm(A) ≝ {X: A ≡m X}.

به درجه چند-یک (≡m) درجه نگاشتی (Mapping Degree) نیز گفته می‌شود.

با توجه به این که داریم ℕ ≰ m ∅↝ بنابراین:

degm(∅) ≠ degm(ℕ).

به عبارت دیگر:

degm(∅) = {∅}, degm(ℕ) = {ℕ}.

■ کارزدن روش کاهش در اثبات تصمیم ناپذیری

روش کاهش (Reduction method) یکی از دو روش عمده (دیگری روش قطری) در اثبات تصمیم‌ناپذیری یک مسئله نوعی است. افزون بر آن، روش کاهش رایج‌ترین روش برای رده‌بندی مسئله‌های تصمیم‌گیری با توجه به حل الگوریتمیک آنها است. الگوی کار روش کاهش در اثبات تصمیم‌ناپذیری بسیار ساده است. فرض کنید Q مسئله‌‌ای باشد که می‌خواهیم تصمیم‌ناپذیری آن را نشان دهیم. اگر بتوان مسئله P را یافت، به گونه‌ای که:

۱- دانسته باشد P تصمیم‌ناپذیر است،

۲- P ≤m Q.

آنگاه می‌توان تصمیم‌ناپذیری Q را نتیجه گرفت↝.

در بندهای قبل بطور مستقل با بهره از روش قطری نشان دادیم K↝ و K⚬↝ تصمیم‌ناپذیر هستند. در اینجا می‌خواهیم نشان دهیم درجه تصمیم‌ناپذیری آنها یکسان است، یعنی داریم:

K⚬ ≡m K .

برای این کار یک بار نشان می‌دهیم K⚬≤mK و بار دیگر نشان می‌دهیم K≤mK⚬.

برای نشان دادن K⚬ ≤m K فرض می‌کنیم K تصمیم‌پذیر است و می‌نویسیم:

۱

۱.۱- فرض برهان شرطی↝: K = {i: φi(i)↓} تصمیم‌پذیر است.

۲.۱- بنا به تابع جفت‌ساز↝ (↜ℕ×ℕ≙ℕ) می‌نویسیم:

K = {i: φi(i)↓} ≙ {<j, k>: φ<j, k>(<j, k>)↓} = K⚬.

۳.۱- K⚬ تصمیم‌پذیر است.

۲ ۱.۱ - ۳.۱ و C.P.: اگر K تصمیم‌پذیر باشد آنگاه K⚬ تصمیم‌پذیر است.

پس طبق آنچه در باره کاهش‌پذیری در بالا گفته شد↝، K به K⚬ کاهش‌پذیر است [یعنی، درجه تصمیم‌ناپذیری↝ مسئله K سخت‌تر (بیشتر) از درجه تصمیم‌ناپذیر مسئله K⚬ نیست].

در برهان بالا، ما در یک روند کارآمد (یعنی ارایه یک الگوریتم) نشان دادیم مسئله K⚬ به K تحویل‌پذیر (کاهش‌پذیر) است. این یعنی: K⚬≤mK. به عبارت دیگر، نشان دادیم درجه تصمیم‌ناپذیری مسئله K⚬ بیشتر از درجه تصمیم‌ناپذیری مسئله K نیست.

افزون بر آن می‌توان گفت:

۳ از ۲ و ترانهش: اگر K⚬ تصمیم‌نا‌پذیر باشد آنگاه K تصمیم‌‌نا‌پذیر است.

برای نشان دادن K≤mK⚬ فرض می‌کنیم K⚬ تصمیم‌پذیر است و می‌نویسیم:

۴

• اگر K⚬ تصمیم‌پذیر باشد آنگاه K تصمیم‌پذیر است:

K⚬= {<i, x>: φi(x)↓} ≙ {<i, i>: φi(i)↓} =
= {i: φi(i)↓} = K.

۵- نیز: اگر K تصمیم‌نا‌پذیر باشد آنگاه K⚬ تصمیم‌‌نا‌پذیر است.

پس طبق آنچه در باره کاهش‌پذیری در بالا گفته شده است K⚬ به K کاهش‌پذیر است (یعنی، درجه تصمیم‌ناپذیر مسئله K⚬ بیشتر از درجه تصمیم‌ناپذیر مسئله K نیست).

بنابراین از ۱ و ۴: K تصمیم‌پذیر(‌نا‌پذیر) است اگر و تنها اگر K⚬ تصمیم‌پذیر(‌نا‌پذیر) باشد. بنابراین می‌نویسیم:

K ≡m K⚬.

و از اینجا: درجه تصمیم‌ناپذیری مسئله K⚬ با درجه تصمیم‌ناپذیری مسئله K یکسان است.

نتیجه:

فرض کنید A یک مجموعه رایانش‌پذیر باشد، آنگاه داریم↝:

A ≤m K.

• برای هر مجموعه رایانش‌پذیر برشمردنی A داریم:

A ≤m K.

• اثبات:

از آنجا که A یک c.e است، پس می‌نویسیم↝:

A = {n ∈ ℕ: ∃yR(n, y)} - بازگشتی R .

اکنون تابع f که در زیر تعریف شده است را در نظر بگیرید:

f(x) = μy R(x, y).

تابع f‌ وقتی معین است که داشته باشیم:

f(x) = ∃y R(x, y).

نیز f یک تابع μrc است و داریم:

∀x∃i f(x) ≃ φ i(x).

بنابراین:

x ∈ A ⇔ φ i(x)↓.

به عبارت دیگر:

A ≤m K⚬.

اما داریم:

K⚬ ≤m K.↜

بنابراین:

A ≤m K.

☜: گیریم X یک مجموعه c.e تصمیم‌ناپذیر (مانند K) باشد. آنگاه چنین نیست که داشته باشیم X≤mX↝ (یعنی داریم  X≰mX).

از آنجا که X یک مجموعه تصمیم‌ناپذیر است، پس X یک c.e نیست. اگر X≤mX پس  X یک c.e می‌بود، که این خلاف فرض بود.

☜ نتیجه:

K ≰m K و K⚬ ≰m K⚬

مجموعه کامل

■ مجموعه کامل (چند-یک) - (m-Complete set)

تعریف: گیریم cc.e کلاس مجموعه‌های رایانش‌پذیر برشمردنی باشد. مجموعه رایانش‌پذیر برشمردنی B (یعنی، B∈cc.e) را مجموعه کامل (چند-یک) (m-Complete) گوییم اگر برای هر مجموعه متعلق به cc.e مانند A داشته باشیم:

A ≤m B.

☚: با توجه به قضیه آمده↝ در بالا، K یک مجموعه کامل است و ازآنجا که

K ≡m K⚬↜

K⚬ نیز کامل است.

در اینجا این قسمت از مرور ما در بحث نظریه رایانش پایان می‌یابد. در یادداشت‌ بعد به دو قضیه بنیادی در نظریه رایانش (قضیه رایس و قضیه بازگشت) و نتایج برآمده از آنها خواهیم پرداخت.

منابع و ارجاعات

1- Davis, Martin, editor. The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.

2- Davis, Martin. The Universal Computer: The Road from Leibniz to Turing. CRC Press/Taylor & Francis Group, 2018.

3- Davis, Martin,  Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.

4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf

5- Stephen Cole Kleene. Mathematical logic, Dover Publications (December 18, 2002).

6- Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, (1980.)

7- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.

8- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing.  (2011).

9- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)

10- George Tourlakis, Computability, Springer International Publishing. (2022.)

11- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. (2015.)

12- Hartley Rogers, Jr· Theory of Recursive Functions and Effective Computability. The MIT Press; Fifth Printing edition (April 22, 1987).

13- Herbert B. Enderton An Introduction to Recursion Theory. Academic Press is an imprint of Elsevier (2011).

14. Dean, Walter, "Recursive Functions", The Stanford Encyclopedia of Philosophy (Winter 2021 Edition), Edward N. Zalta (ed.)

◄ توجه: