از آنجا که همه عبارت‌ها توسط عبارت‌های دیگر تعریف می‌شوند، اگر قرار است نقطه آغازین داشته باشیم، دانش بشر همیشه باید پذیرای عبارات قابل درک بدون تعریف باشد.
.
مجموعه
.
Set
.
یک مجموعه گردایه‌ای از چیزهای معین و قابل تمیز در شهود و خرد است که همچون یک کل درک گردد.
مجموعه‌ها و درواقع "نظریه مجموعه‌ها" یک
نظریه استنتاجی➥
[*]- در ادامه یادداشت‌های منطق، تئوری استنتاجی و نیز دستگاه‌های اصل موضوعی مورد ملاحظه قرار خواهند گرفت.
است که به‌وسیله جرج کانتور بنیاد گردیده. ریاضی‌دانان با چندین رهیافت این نظریه را بیان می‌کنند.
ازجمله, نظریه طبیعی مجموعه‌ها➥
P. R. Halmos, "Naive Set Theory", Springer, 1974 -1998.
است که در آن بهره‌وری از زبان طبیعی حداکثری است. اما بیان
گوهری آن توسط
دستگاه‌های اصل موضوعی است. ازجمله
دستگاه‌های اصل موضوعی مجموعه‌ها، دستگاه موسوم به
زیملو-فرانکل/ Zermelo-Fraenkel با کوتاه شده
ZF است. این
دستگاه به شمول اصلی موسوم به
اصل انتخاب/ Axiom of Choice (که در ادامه با همین عنوان آن را خواهیم دید) با کوته‌سازی
ZFC و گاهی
ZF+C، بنیاد ریاضیات جاری است. دستگاه دیگر موسوم به
Neumann-Bernays-Godel با کوته‌سازی
NBG است. دستگاه
NBG و ZFC بسیار شبیه و همساز هستند. تفاوت عمده در وجود
چیزی بنام "کلاس" در دستگاه
NBG است که مجموعه به‌عنوان
گونه‌ای از آن معرفی می‌گردد. در بند ۲.۱، کلاس و مجموعه، کمی بیشتر
دراین‌باره توضیح خواهد آمد.
آنچه در پی و قسمت‌های بعد خواهد آمد صرفاً معرفی بعضی واژگان این نظریه است که در ادامه
نگاه نزدیک‌تر به منطق (و نیز رایانش) به آن‌ها نیازمندیم. علت این نیاز ازجمله دقت و ژرفی، درعین‌حال سادگی آن‌هاست و اگر بتوانیم آن‌ها را بجا به کار ببریم، هر بار از چندین و چند صفحه توضیحات، که خود می‌توانند باعث ابهام و
چندمعنایی در کلام شود، جلوگیری خواهد شد.
☚ مرور نظریه
اصل موضوعی مجموعه‌ها (ZF و NBG) را می‌توان در
دستگاه صوری مجموعه‌ها یافت.
■ مجموعه و عضویت
داستان را از فرد معینی بنام پرویز آغاز کنیم که هرروز صبح فرزند خود را از مسیر مشخص به مدرسه می‌رساند. وی درراه مدرسه هرروز چیزهای ثابتی، مانند تابلوی یک دندان‌پزشک، یک کیوسک مطبوعاتی، ماشین پارک شده مدیر مدرسه, خدمتگزار مدرسه، باجه تلفن و مانند آن‌ها را می‌بیند. وی می‌تواند برای همه این چیزها یک نام انتخاب و ازآن‌پس با آن نام از آن‌ها یاد کند. فرض کنیم نام انتخابی وی ""
باشد. اکنون می‌توان گفت نام یک مجموعه است و تعریف (تعریف مجموعه و نه تعریف مجموعه) می‌تواند "چیزهایی که پرویز در مسیر روزانه رساندن فرزند خود به مدرسه می‌بیند" باشد. به هر یک از این چیزها
گفته: یک
عضو
هستند [یا
عنصر
یا در هستند، یا تعلق
به دارند.]
در متونی که از زبان ریاضی برای گویایی و دقت بهره می‌برند، عبارت‌هایی کم‌و‌بیش مثل "فرض کنید ∑ یک مجموعه باشد ..." بسیار
دیده می‌شود. در این
موارد، اول و مهم‌ترین چیز این است که قرار است عناصری در میدان بحث بیایند که ازجمله عضو
∑ (یعنی عضو یک مجموعه) خواهند بود و بنابراین
نقش اول آن‌ها عضویت در مجموعه نام داده‌شده‌ای است. اینکه، این عناصر چه هستند یا اصلاً وجود دارند
یا نه، مسئله بعد است.
در ادامه این یادآور، فقط بر مبنای همین‌که گفته شد و پس
از بیان چند خاصیت مجموعه‌ها، ساختارهای ساخته‌شده‌ای (برای
مثال در دانش کامپیوتر و رایانش) را می‌بینیم و
مفاهیم بس مهمی چون شمارش، شمارش‌پذیری، مقایسه، مقایسه‌پذیری، انتخاب -اصل عجیب انتخاب،
ترتیب، ترتیب‌پذیری، بی‌نهایت، بی‌نهایت‌ها و بسیاری دیگر را مرور خواهیم کرد.
■ کلاس و مجموعه
در بیشتر متون مقدماتی تا متوسط منظور از رده یا کلاس همان مجموعه است؛ با این اشاره ضمنی که اعضای آن خود هریک نام (یا نماینده) مجموعه‌های از پیش معینی می‌توانند باشند؛ یا اعضای آن اعضای یک مجموعه گسترده‌تر هستند ولی تأکید بر ویژگی یا ویژگی‌های مشخصی
است که ممکن است همه اعضای آن مجموعه گسترده‌تر دارای این ویژگی(ها) نباشند. اما در سطح فنی‌تر (برای مثال، در دستگاه
NBG که در بند ۱.۱ آمد)،
کلاس
یک چیز ابتدایی (تعریف‌نشده) است. در این دستگاه علاوه بر کلاس، "∈" نیز یک
تعریف‌نشده دیگر است و فقط هم همین دو تعریف‌نشده هستند.
فرض کنید C۱
و C۲ کلاس
باشند، آنگاه می‌نویسیم: C۱∈C۲و به زبان فارسی می‌خوانیم: C۱ عضو C۲ است (یا
C۱ به C۲ تعلق دارد، یا C۱
در C۲ است و مانند آن‌ها).
در این رهیافت کلاس‌ها در دو سته متمایز می‌شوند:
۱- کلاس سره:
کلاسی که عضو هیچ کلاسی نیست.
۲-
مجموعه: کلاسی که عضو بعض کلاس
است [به چنین کلاس عنصر هم گفته می‌شود.]
بنابراین، همه مجموعه‌ها کلاس
هستند ولی همه کلاس‌ها مجموعه نیستد. به‌عبارت‌دیگر، بعضی کلاس‌ها (کلاس‌های
سره) گسترده‌تر از آن‌اند تا
مجموعه باشند.
به‌عنوان‌مثال، کلاس همه مجموعه‌ها یک
کلاس سره است. در ادامه (بند
۷.۱، نمایاندن مجموعه و
پارادوکس
راسل) توضیح بیشتر
خواهد آمد.
دقیق و مشروح دستگاه
NBG را نیز می‌توان در:
آنگونه که
نورمن استین
رد
/ Norman Steenrod آن را نامید،
زبان کتگوری‌ها از روی لطف همچون
"مهمل انتزاعی" شناخته‌شده.
در اصل، این عبارت نه ضرورتاً موهن که دقیق هم است: کتگوری‌ها به "مهمل" بدین
برداشت رجوع دارند که آن‌ها تماماً درباره "ساختار" هستند و نه درباره "معنی" آنچه را که
نشان می‌دهند. __ پائولو الفی
/ Paolo Aluffi.
مجموعه‌ها را با چیزهای متعلق به چیزها آغاز کردیم. به همین
ترتیب می‌توان کتگوری
(کتگوری) (نظریه کاتگوری‌ها) را با چیزهایی در ساختارها (یا بر ساختارها)
آغاز کرد. نظریه کاتگوری‌ها بررسی ساختارها است که ازجمله، یکسانی‌های ارزشمند را بین
چیزهای (ساختارهای) به‌ظاهر بی‌ربط آشکار می‌کند. آغازگر این نظریه
ساموئل النبرگ
(Samuel Eilenberg,
۱۹۰۹-۲۰۰۵) و
ساندرز مک لین
(Saunders Mac Lane, ۱۹۱۳-۱۹۹۸)
،که به‌تمامی به شیوه اصل موضوعی گسترش‌یافته، هستند. در این نظریه، مجموعه خود
گونه‌ای کتگوری است (یعنی، همه مجموعه‌ها کتگوری هستند.) نظریه کتگوری‌ها
دارای دو چیز ابتدایی به‌قرار چیز و
پیکانه (نشانک) است که در آن
پیکانه‌ها از چیزها به چیزها نشانه رفته‌اند.
در نمودار شماتیک زیر یک کتگوری شامل سه چیز
و شش پیکانه نشان داده‌شده.
شکل ۱.۲.۱- یک کتگوری با سه چیز و شش پیکانه.
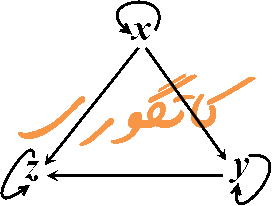
نظریه کتگوری‌ها، به‌جز در خود ریاضی که همچون
زبان جهانی ریاضی مطرح است، در دانش کامپیوتر، علوم
شناختی و فلسفه کاربردهای مهم خود را نیز دارا است.
■ منابع
☚
عبارت
کتگوری در
نظریه کتگوری که این‌جا بدان اشاره شده با مقولات ارسطویی(Aristotle's Categories) یا
گزاره‌های حملی (نیز
قیاس‌های حملی) بدون ارتباط است و بنابراین نباید به آن‌ها (واژگان ارسطویی)
ربط داده شود.
"
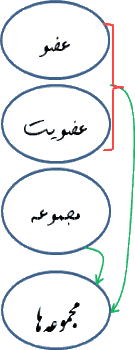
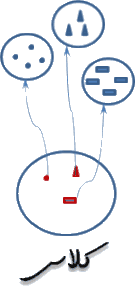
باشد. اکنون می‌توان گفت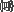 
(تعریف مجموعه 
