■ مقدمه:
گرچه کوشش شده تا آنچه میآید خودبسنده باشد، بااین‌حال قسمت کلاس، عضویت و مجموعه پیش‌فرض انگاشته شده و قسمت اصول موضوعه در دستگاه ZF (۱) البته کارساز خواهد بود. در ادامه هر جا نیاز است پیوند‌های لازم با کارکرد پنجره‌ای آمده است.
■ مجموعه‌های مساوی:
مجموعه‌ها دو به دو مساوی‌اند اگر و فقط اگر عضوی دریکی نباشد که در بقیه باشد. بنابراین هر مجموعه با خودش مساوی است. نیز اگر B ،A و C مجموعه باشند؛ اگر A مساوی B باشد (یعنی، A=B) آنگاه B نیز مساوی A است (یعنی، B=A)؛ همچنین، اگر A مساوی B و A مساوی C باشد آنگاه B مساوی C است.
• اصل موضوع گسترش را ببینید.
Equality of Sets: Example 2
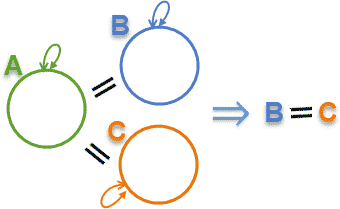
فرض کنید A مجموعه اعداد صحیح زوج مثبت باشد. B را مجموعه اعداد صحیح مثبتی می‌گیریم که حاصل جمع دو عدد فرد مثبت باشند. نشان می‌دهیم A = B.
۱- گیریم x عضو A باشد. پس:
۱. x=۲m
۲. x=(۲m-۱)+۱
۳. از ۲ نتیجه می‌شود x عضو B است
۲- گیریم x عضو B باشد. پس:
۱. x=(۲p-۱)+(۲q-۱)
۲. x=۲(p+q-۱)
۳. از ۲ نتیجه می‌شود x عضو A است
از ۱ و ۲ داریم: A = B.
■ مجموعه تهی:
گاهی صحبت از گردیه‌ای از اعضای مجموعه‌ای از طریق وصف آنها می‌کنیم. اگر نشان دهیم جواب به پرسش وجود هر چیز در این گردایه قطعاً منفی است (یعنی، هیچ‌چیز مطابق آن وصف وجود ندارد)، آنگاه مجموعه‌ای داریم که خالی/تهی است. برای مثال اگر وصف اعضای گردایه‌ای، به فرض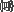 
، "اعداد صحیح مضرب ۳ بین ۶ و ۹" باشد، آنگاه مقدار ارزش گزاره "هر عنصر 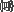کوچک‌تر از ۹ و بزرگ‌تر از ۶ است" درست ولی پاسخ پرسش پیش‌تر گفته منفی است؛ بنابراین 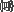می‌تواند یک مجموعه و نیز یک مجموعه تهی باشد. بنابراین، چنین نیست که همه مجموعه‌ها عضو داشته باشند. از تساوی مجموعه‌ها میتوان نتیجه گرفت؛ همه مجموعه‌های تهی مساوی‌اند و میتوان نشان معروف "∅" را به آن داد و از همه آنها با ∅ یادکرد.
• اصل وجودی، را ببینید.
■ زیرمجموعه
فرض کرده A و B دو مجموعه باشند، A را زیرمجموعه B گویند (و می‌نویسند: A⊆B) اگر و فقط اگر عضوی نباشد که در A باشد ولی در B نباشد. فی‌البداهه مجموعه تهی زیرمجموعه هر مجموعه‌ای است و هر مجموعه زیرمجموعه خودش است. بنابراین یک مجموعه تهی چندان هم بی‌چیز نیست و یک زیرمجموعه دارد. آشکار است که، اگر دو مجموعه زیرمجموعه هم باشند آنگاه آن دو مجموعه مساوی‌اند و نیز وارون آن. بنابراین:
(A⊆B) ∧ (B⊆A) ⇔ A=B.
• درستی تهی (سالبه به انتفای موضوع) را ببینید.
■ زیرمجموعه سره و ناسره:
گیریم؛ A⊆B. به A یک زیرمجموعه سره B میگویند وقتی عضوی در B هست که در A نیست (یعنی وقتی A≠B). در این حالت در صورت نیاز برای تأکید می‌نویسند A⊂B. بنابراین، ∅ زیرمجموعه سره همه مجموعه‌های ناتهی است و همین‌طور هر مجموعه زیرمجموعه ناسره خود است. از واژه "سره" در ریاضی کم استفاده نمی‌شود. برای مثال، مراد از مقسوم‌علیه سره یک عدد صحیح، مقسوم‌علیه‌های آن عدد به‌جز خود آن عدد است و همین‌طور کلاس سره که در ۲.۱ دیدیم.
■ نمایاندن مجموعه:
معمولاً یک مجموعه خاص با بیان ویژگی [خاصیت] اعضایش (مفهوم آنها) یا با قرار دادن عضوها یا نشانه ویژه عضوها درون یک جفت آکولاد تعریف می‌شود (مصداق آنها). [البته نه هر خاصیتی- به پارادوکس راسل که در ادامه میآید توجه نمایید.] مجموعه تهی را با { } نمایش، همچنین عضویت (تعلق) و زیرمجموعه بودن را به ترتیب با نمادهای '∈' و '⊂' نشان می‌دهند. معمولاً به‌جای آنکه بگویند: چنین نیست که x(شیئی) متعلق به A است — می‌نویسند: x∉A. به همین ترتیب '⊄' برای زیرمجموعه نبودن است. بعضی جاها از نماد '⊂' برای زیرمجموعه سره بودن و '⊆' برای زیرمجموعه بودن استفاده می‌شود.
•مثال⤺
در زیر مثال‌هایی از نمایش مجموعه را میتوان دید:
۱- {۰, ۱} ۲- {۱, ۰} ۳- {{۲, ۳}} ۴- {{۱}, {۱, ۲}}
۵- {{۲, ۳}} ۶- {۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, . . .} ۷- {۱, ۰, ۱}
۸- {x: عدد مثبت و مساوی حاصل جمع مقسوم‌علیه‌های سره خود x}
۹- {۱} ۱۰- {{۱}}
در این مثال‌ها مجموعه ۳ تهی است. در ۴ باید دقت کرد که ۱ و ۲ عضوهای این مجموعه نیستند بلکه فقط مجموعه‌های {۲ ،۱} و {۱} عضوهای آن هستند و این مجموعه فقط دو عضو دارد. مجموعه ۵ فقط یک عضو دارد. در ۶ معنی سه‌نقطه آخر "و مانند آنها" است، یعنی انتظار می‌رود که ما بقیه عضوها را خواهیم شناخت. مجموعه مثال ۷ و ۱ مساوی هستند. به‌عبارت‌دیگر برای هر چیز x داریم: {x, x}={x}. مجموعه ۸ مجموعه اعداد کامل است؛ مانند ۶ که برابر است با ۱+۲+۳ و همین‌طور ۲۸، ۸۱۲۸ و مانند آنها. دو مجموعه ۹، ۱۰ هردو تک عضو و با اعضای متمایز هستند، یعنی ۱ و {۱} دو چیز متمایز هستند. یکسان فرض کردن آنها مثل این است که بگوییم هر دارنده یک‌چیز خود همان یک چیز است [یک جعبه دارای یک سیب خودش یک سیب است.
•مثال⤺
فرض کنید: A = {∅, {∅}, {∅, {∅}}} در این صورت، عبارات زیر درست‌اند:
۱. ∅⊂A
۲. ∅∈A
۳. {∅}∈A
۴. {∅}⊆A
۵. {{∅}}⊂A
۶. {∅, {∅}}⊆A
۷. {∅, {∅}}∈A
۸. {∅, {∅}, {∅, {∅}}}⊆A
■ پارادوکس راسل
آن‌طور که دیدیم در مثال ۸:
{x: عدد مثبت و مساوی حاصل جمع مقسوم‌علیه‌های سره خود x}
ممکن است بتوان یک مجموعه را با خاصیت اعضای آن مطابق یکی از قالب‌های زیر تعریف کرد [در زیر P هر ویژگی دلخواهی است و Px به‌صورت "x دارای ویژگی P است خوانده می‌شود]:
۱- Δ = {x ∈A: Px}
مجموعه‌ای که شامل آن عضوهای A است که دارای خاصیت P هستند.
۲- Δ = {x: x∈A, Px}
مجموعه‌ای که اعضای آن عضو A و دارای خاصیت P هستند.
۳- Δ = {x:Px}
مجموعه‌ای که اعضای آن دارای خاصیت P هستند.
در ۱ و ۲ بالا مجموعه Δ به‌عنوان زیرمجموعه A تعریف‌شده و میتوان نوشت: Δ⊂A. اما تعریف مجموعه‌ای به قالب ۳ قدرتمندتر [فراگیرتر] ازآنچه می‌تواند باشد است. در پاراگراف بعد خواهیم دید چرا این‌گونه قدرتمندی نابودی خود را در خود دارد. معنای دقیق ویژگی ببینید.
برای مثال، مجموعه F را مجموعه همه مجموعه‌هایی بگیرید که خود عضو خود نیستند. به‌عبارت‌دیگر، P را ویژگی x∉x گرفته و می‌نویسیم:
F = {x:Px) = {x:x ∉ x}.
اگر F وجود داشته باشد آنگاه تهی نخواهد بود. زیرا، برای مثال، مجموعه مادران تک‌فرزند عضو F است و آشکار است که مجموعه مادران تک‌فرزند خود یک مادر تک‌فرزند نیست. در پاراگراف بعد به این می‌پردازیم که فرض وجود این مجموعه و بنیاد ریاضیات بر این‌چنین نظریه مجموعه‌ای موجب می‌شود تا هر حکم ریاضی اثبات پذیر باشد. یعنی، هر گزاره ریاضی درعین‌حال که درست، درعین‌حال نادرست هم باشد. [برای توضیح درباره این نتیجه بحث ناسازگاری - فصل دهم کتاب را ببینید.]
اکنون می‌پرسیم آیا F عضو خود است؟
اگر F ∈ F، آنگاه به‌موجب P داریم F ∉ F.
اگر F ∉ F، آنگاه به‌موجب P داریم F ∈ F.
آشکارا این، یک تناقض است و برخاسته از قالب ۳ (وصف بی‌حدومرز) در بالا برای تعریف یک مجموعه است. بنابراین (در نظریه طبیعی مجموعه‌ها) چنین نیست که هر وصفی از اشیاء مولد یک مجموعه شود. این به پارادوکس راسل معروف است.
• مجموعه‌ی همه مجموعه‌ها را ببینید.
• تعریف یک مجموعه به‌صورت {x:x∈A, x ∉ x} بدون مشکل است و مشمول پارادوکس راسل نیست. تعریف این مجموعه مطابق قالب ۲ است.
گوتلوب فرگه از وضع‌کنندگان اصلی منطق جدید کلاسیک (و مخترع منطق محمولات اصل موضوعی) در کتابی که برای نظم و نسق منطقی ریاضیان منتشر نمود (Begriffsschrift / مفهوم نگاری، ۱۸۷۹) قالب ۳ را به‌عنوان مولد مجموعه پذیرفته بود. برتراند راسل بعد از خواندن کتاب پی به این پارادوکس برد (ازاینجا این پارادوکس بنام راسل مشهور است) و از طریق نامه به اطلاع فرگه رساند. این باعث شد به استحکام بنای در حال ساخت ریاضیات که در آن زمان بسیار مورد اهتمام ریاضیدانان بود موقتاً خلل وارد شود. درواقع حذف این اصل (قالب ۳) از دستگاه فرگه موجب ناکارایی دستگاه می‌گردید (آن را بیش‌ازاندازه ضعیف می‌کرد). چندان طول نکشید که برتراند راسل با ارائه نظریه گونه‌ها /Russell's theory of types این مشکل را از سر راه نظریه مجموعه‌ها برداشت و سپس نیز دستگاه موسوم به دستگاه زیملو-فرانکل /Zermelo–Fraenkel معروف به ZF+C برای مجموعه‌ها [قوی‌ترین بنیاد دستگاه ریاضیات جاری/کلاسیک] ارائه گردید. ناگفته نماند که از دستگاه فرگه فقط همین یک اصل(قالب ۳) مشکل‌آفرین بود. همه اصول دیگر فرگه باقوت در دستگاه‌های بعدی نقش بنیادی خود را دارند.
■ اعمال روی مجموعه‌ها:
اشتراک مجموعه‌ها: مجموعه C را اشتراک دو مجموعه A و B گویند اگر و فقط اگر عضوی در C نباشد که در A و B نباشد, و می‌نویسند C=A ∩ B. دو مجموعه از هم جدا هستند اگر اشتراک آنها تهی باشد.
اجتماع مجموعه‌ها: مجموعه U را اجتماع دو مجموعه A و B میگویند اگر و فقط اگر عضوی در U نباشد که در A یا در B (یا در هردو) نباشد, و می‌نویسند U=A∪B.
تفاضل مجموعه‌ها: مجموعه D را تفاضل مجموعه B از A گویند و نوشته:
D = A - B ، [همچنینD = A / B ]
اگر و فقط اگر عضوهای D همه عضوهایی باشد که در A هست و در B نیست.
متمم مجموعه: گیریم D =A / B، آنگاه به D متمم مجموعه A نسبت به B میگویند. اگر A و B از هم جدا باشند آنگاه:
A = A - B و B = B - A.
اگر درزمینهٔ بحث چنین پیش‌فرض باشد که همه مجموعه‌ها زیرمجموعه یک مجموعه تثبیت‌شده مانند M هستند (برای مثال بحث درباره اعداد)، آنگاه به M-A متمم A گفته و آن را با 'A نشان می‌دهند.
• اصل موضوع اجتماع را ببینید.
■ مجموعه توانی
به مجموعه‌ای که اعضای آن همه‌ی زیرمجموعه‌های یک مجموعه باشند مجموعه توانی آن مجموعه میگویند.
فرض کنید؛ {۱ ,۰}=B آنگاه: {{۱ ,۰} ,{۱} ,{۰} ,{ }} که آن را با Ƥ(B) نشان‌گذاری می‌کنند، مجموعه توانی B است. اگر تعداد اعضای یک مجموعه n باشد، تعداد اعضای مجموعه توانی آن ۲n است و از اینجاست که نام "توان" آمده است. در زیر چند مثال آمده است:
Ƥ(ø)={ø} ۲۰=۱.
Ƥ({۱}) = {ø, {۱}} ۲۱=۲.
Ƥ({۱,۲}) = {ø, {۱}, {۲}, {۱, ۲}} ۲۲=۴.
Ƥ({۱,۲,۳})={ø, {۱}, {۲}, {۳}, {۱, ۲}, {۱, ۳}, {۲, ۳}, {۱, ۲, ۳}} ۲۳=۸.
Ƥ(Ƥ(ø))=Ƥ({ø})={ø, {ø}} ۲۱=۱
Ƥ(Ƥ(Ƥ(ø)))=Ƥ({ø, {ø}})={ø, {ø}, {{ø}}, {ø, {ø}}} ۲۲=۴.
• اصل موضوع مجموعه توانی را ببینید.
■ روش مکانیکی برای یافتن اعضای مجموعه توانی(۱)
مجموعه توانی {T={p, q, r را بیابید:
فرض کنید اعضای T گزاره‌های ساده یک صورت گزاره‌ای باشند. اعداد ۱ تا ۳ را به‌دلخواه به آنها گمارده(منتسب می‌کنیم). فرض کنید این گماردن به‌قرار: ۱↔p و ۲↔q و ۳↔r باشد. سپس سه ستون راهنمای جدول-ارزش این صورت گزاره‌ای فرضی را تشکیل می‌دهیم. از روی آن به شیوه زیر میتوان اعضای مجموعه توانی را حساب کرد.
| pqr | ۱ ۲ ۳ |
| 111 | {p, q, r} |
| 110 | {p, q } |
| 101 | {p, r} |
| 100 | {p } |
| 011 | { q, r} |
| 010 | { q } |
| 001 | { r} |
| 000 | { } |
■ الگوریتم / روش مکانیکی برای یافتن اعضای مجموعه توانی(۲)
مجموعه‌های A={a۱, a۲, a۳, . . . an} و Ƥ=ø را داریم. روند کارآمد [الگوریتم] زیر همه زیرمجموعه‌های A را محاسبه و در Ƥ(A) می‌گذارد.
| گام | دستور برای اجرا |
| ۱- | مجموعه تهی را به Ƥ بیافزای (Ƥ⋃ø↦Ƥ)؛ |
| ۲- | مقدار متغیر i را ۱ قرار ده ( ۱↦i)؛ |
| ۳- | برای هر عضو Ƥ، به فرض X، مجموعه C=X⋃{ai} را بساز و به Ƥ بیافزای (Ƥ⋃C↦Ƥ)؛ |
| ۴- | اگر: i<n آنگاه به مقدار i یک واحد بیافزای (i+۱↦i) و اجرا را از قدم ۳ پیگیر باش؛ وگرنه: اجرا را از قدم ۵ پیگیر باش؛ |
| ۵- | پایان اجرا. |
باید نشان داد این الگوریتم ۱- در زمان محدود به پایان می‌رسد؛ ۲- صحیح است، یعنی در پایان در Ƥ همه زیرمجموعه‌های A حضور دارند.
| در این جدول پیگیری اجرای الگوریتم برای A={a۱, a۲, a۳} آمده. | ||
| شماره گام | i | Ƥ |
| ۱ | # | ø |
| ۲ | ۱ | |
| ۳ | ۱ | {a۱} |
| ۴ | ۲ < ۳ | |
| ۳ | ۲ | {a۲}, {a۱, a۲} |
| ۴ | ۳ <> ۳ | |
| ۳ | ۳ | {a۳}, {a۱, a۳}, {a۲, a۳}, {a۱, a۲, a۳} |
| ۵ | ۴ | پایان |
■ افراز مجموعه
گیریم S یک مجموعه ناتهی باشد. به مجموعه P یک افراز مجموعه S گوییم اگر P شامل زیرمجموعه‌هایی ناتهی و دوبه‌دو از هم جدای S بوده به قسمی که اجتماع آنها S باشد.
به‌عبارت‌دیگر، P یک افراز S است اگر و فقط اگر:
۱- P زیرمجموعه سره مجموعه توانی S باشد [P ⊆ Ƥ(S) - {∅}]؛
۲- برای هر A و B متعلق به P آنگاه (A≠B ⇒ (A⋂B)=∅)؛
۳- P = S⋃.
•مثال⤺
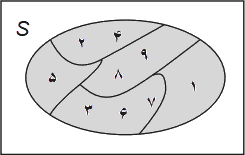
اگر S = {۱, ۲, ۳,۴ ,۵ ,۶ ,۷ ,۸ ,۹} آنگاه
P = {{۱}, {۲, ۴}, {۳, ۶, ۷}, {۵} ,{۸, ۹}}
یک افراز S است.
•مثال⤺
اگر S = {۱, ۲, ۳} آنگاه همه مجموعه‌های زیر افرازهای S هستند.
P۱ = {{۱}, {۲}, {۳}}
P۲ = {{۱,۲}, {۳}}
P۳ = {{۱, ۳}, {۲}}
P۴ = {{۲, ۳}, {۱}}
P۵ = {{۱, ۲, ۳}}.
■ مشاهیر مجموعه‌ها:
از مشاهیر مجموعه‌ها یکی مجموعه تهی است که معرفی شد و دیگری مجموعه اعداد طبیعی است که معرف حضور است و آدمیزاد می‌خواهد هر چیزی را فقط با آن بشمرد کند. یکی از سیارات نیز همین سیاره شمارش است (اخترک چهارم/شازده کوچولو). مجموعه اعداد طبیعی یعنی {۰, ۱, ۲ ,۳, . . .} نیز مثل ∅ نشان مخصوص خود، یعنی 
را دارد. اعضای این مجموعه ازجمله مهم‌ترین‌های دنیا و همین‌طور پرسابقه‌‌ترین هستند. مجموعه از مجموعه‌های با سر بی ته است.
• تعریف عدد طبیعی را ببینید.
مجموعه بعدی مجموعه اعداد صحیح نام و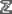 
را نشان دارد. 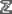همه اعضای را دارد [ولی بی‌سر و بی ته] و به‌قرار {. . . ،۲ ، ۱، ۰، ۱-، ۲-، . . .} است.
مجموعه بعدی مجموعه اعداد گویا نام و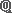 
را نشان دارد. این مجموعه همه عضوهای 
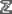را دارد بعلاوه اعداد با حداقل یک رقم اعشاری غیر صفر. تعداد ارقام اعشاری می‌توانند (نامتناهی) باشند و البته باید از جای معینی به بعد رشته متناهی از آنها تکرار شود. اعداد گویا درواقع، اعدادی هستند که حاصل تقسیم دو عدد صحیح هستند (قدیم‌تر تبدیل این اعداد اعشاری به کسری را به هم رفع و تجنیس می‌گفتند.). هر عدد گویا قابل تحویل به کسری است که صورت و مخرج آن نسبت به هم اول باشند (مقسوم‌علیه مشترک جز یک نداشته باشند.)
در عالم اعداد گویا، عدد ۲/۱، یعنی تقسیم دو بر یک، جذر ندارد (اثبات آن چند خط پایین‌تر آمده.) 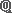برای بقای گویایی باید چنین حفرهای (مانند، جذر ۲) را ندیده بگیرد. و البته این حفره‌ها یکی دوتا هم نیستند. ازجمله عدد معروف پی، یعنی اندازه نسبت محیط دایره به قطر خود که برای هر دایره ثابت است. داستان فیثاغورثیان و اندازه وتر مثلث قائم‌الزاویه متساوی‌الساقین با ساق‌های به‌اندازه ۱، خود به‌اندازه اعداد گویا مشهور است.
مجموعه‌ای که علاوه بر اعداد گویا حفره‌ها را که به آنها اعداد گنگ می‌گوییم داشته باشد، به مجموعه اعداد حقیقی معروف و نشان‌دار به 
است.
در انتهای مراسم معرفی: +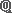 مجموعه اعداد گویای مثبت،* 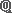مجموعه اعداد گویای غیر صفر هستند و مانند آنها نیز برای ، 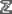و .
■ ناگویایی ریشه دوم ۲:
ناگویایی ریشه دوم عدد گویای ۲
می‌خواهیم نشان دهیم ریسه دوم ۲، یعنی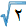 
، عدد گویا نیست. برهان را به شیوه برهان غیرمستقیم پیش می‌بریم:
۱. 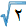گویا است.
۲. اعداد صحیح p و q که نسبت به هم اول هستند وجود دارد به قسمی که:
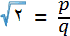
۳.
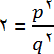
۴.
p۲=۲q۲
۵. p۲ مضرب ۲ است؛
۶. p۲ مضرب ۴ است؛ (هر عدد صحیح زوج مربع مضرب ۴ نیز است)
۷. q مضرب ۲ است؛
۸. p و q دارای مقسوم‌علیه مشترک ۲ هستند؛
۹. اعداد صحیح p و q نسبت به هم اول نیستند.
 |  |