≡
فهرست:
توابع بازگشتی (کامل) – مقدمه‌ای بر منطق و رایانش درآمدی یه منطق

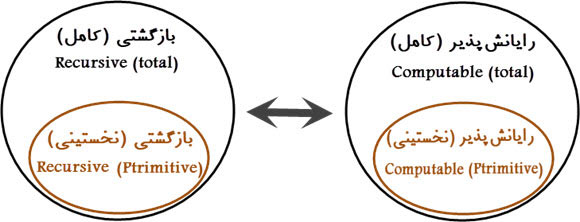
توابع بازگشتی (Recursive Functions)

منطق و نظریه رایانش (۳)

درآمد به منطق

توانایی محدود ما در برابر ساختار بازگشتی در زبان طبیعی یک مهارت اکتسابی است که بر توانایی‌های غیر-زبانی (non-linguistic) ما در یادگیری «توالی» تکیه دارد.

Christiansen, Morten H. and Chater, Nick. (2015) https://wrap.warwick.ac.uk/75681/1/WRAP_Chater_fpsyg-06-01182.pdf

در این یاداشت (نظریه رایانش -۳) از تابعی بحث می‌کنیم که رایانش‌پذیر است اما بازگشتی-نخستینی نیست، به این معنی که نمی‌توان آن را با صورت ساده‌ای از بازگشت تعریف کرد. سپس نشان می‌دهیم که چگونه سیستم توابع بازگشتی-نخستینی را با چرخه‌های آزاد گسترش دهیم تا بتواند همه توابع رایانش‌پذیر را شامل شود. سرانجام، مفهوم مجموعه‌ها و رابطه‌های رایانش‌پذیر و مسئله تصمیم‌ را پیکربندی می‌کنیم.

روند منطق و نظریه رایانش (۳): توابع بازگشتی

■ مقدمه

≡

۱- مقدمه

۷- مسئله تصمیم گیری (Decision problem)

۲- تابع آکرمان (The Ackermann Function)

۸- رابطه رایانش‌پذیر (نیز بازگشتی - تصمیم‌پذیر)

۳- تابع آکرمان یک تابع نخستینی-بازگشت نیست.

۹- جبر تصمیم‌پذیری (Algebra of decidability)

۴- کمینه سازی بی‌کران (Unbounded Minimalization)

۱۰- ویژگی غیر-زبانی (non-linguistic) توابع بازگشتی

۵- توابع بازگشتی (Recursive Function - r.c)

۱۱- منابع و ارجاعات

۶- مجموعه رایانش‌پذیر (نیز بازگشتی - تصمیم‌پذیر)

• بازگشت و تعریف بازگشتی را ببینید.

در یادداشت توابع بازگشتی-نخستینی، با روش برهان قطری نشان دادیم چنین نیست که همه توابع رایانش‌پذیر، توابع p.r باشند↝.

در این یادداشت تابعی را معرفی خواهیم کرد که گرچه رایانش پذیر است و به گونه استقرایی تعریف شده است، ولی بازگشتی-نخستینی نیست. سپس با افرودن یک قاعده دیگر، یعنی امکان چرخه‌های آزاد، دستگاه توابع بازگشتی-نخستینی را برای پوشش تمام توابع رایانش‌پذیر گسترش می‌دهیم. سرآخر، پس از معرفی مجموعه‌ها و رابطه‌های رایانش پذیر، مرور کوتاهی به مسئله تصمیم‌پذیری (Entscheidungsproblem) خواهیم کرد.

■ یادآور

☚: در این قسمت، همه نگاشت‌ها [توابع (کامل) و توابع جزئی]، مگر خلاف آن گفته شده باشد، از مجموعه توانی اعداد طبیعی، یعنی ℕn برای n≥۱، در ℕ تعریف می‌شوند. برای مثال:

f۱ : ℕ۲ → ℕ: f(x۱, x۲) = ۲x۱ + x۲ + ۱.

و به طور کلی:

f(x) : ℕn → ℕ.

☚: مراد از x (یا x<..,k>) دنباله متغیرهای (x۱,...,xk) برای k≥۱ است. برای مثال دنباله متغیرهای (x۱,x۲,x۳).

☚: فرض کنید A و R به ترتیب کلاس و رابطه باشند. ~A و ~R (همچنین A و R) به ترتیب عبارت‌اند از:

~A = A ⇔ {x|x ∉ A} (کلاس متمم)

~R = R ⇔ ~R(x)

• معرفی نماد ≃:

گیریم f و g دو تابع باشند. می‌نویسیم:

f ≃ g

اگر برای هر x داشته باشیم f و g هر دو معین با مقدار مساوی باشند یا هر دو معین نباشند. به عبارت دیگر:

g(x) ≃ f(x)↓ ⇔ (f (x)↑ ∧ g(x)↑) ⋁ ∃z(f (x) = z ∧ g(x) = z).

نیز گیریم Q و R رابطه‌های nتایی باشند. گوییم:

R ≃ Q

اگر برای هر x رابطه‌های R و Q هردو رایانش‌پذیر باشند یا هردو رایانش‌پذیر نباشند.

■ تابع آکرمان (The Ackermann Function)

رشد تابع اکرمن

همان طور که دیدیم، چنین نیست که همه توابع رایانش‌پذیر، توابع P.r باشند↝. در اینجا ابتدا تابع مشهور به تابع آکرمان را معرفی می‌کنیم و نشان می‌دهیم گرچه رایانش پذیر است، اما یک تابع P.r نیست. تعریف این تابع در زیر آمده است:

تابع آکرمان (The Ackermann function) [صورت یکم]
α(۰, m) =m + ۱;
α(n + ۱, ۰) =α(n, ۱);
α(n + ۱, m + ۱) = α(n, α(n + ۱, m )).

محاسبه برخی مقادیر این تابع را در زیر می‌توان دید:

۱: α(۱, ۰) = α(۰, ۱) = ۲
۲: α(۱, ۱) = α(۰, α(۱, ۰) ) = α(۰, ۲) = ۳
۳: α(۱, ۲) = α(۰, α(۱, ۱) ) = α(۰, ۳) = ۴
۴: α(۲, ۰) = α(۱, ۱ ) = ۳
۵: α(۲, ۱) = α(۱, α(۲, ۰) ) = α(۱, ۳) = = α(۰, α(۱, ۲) ) =
= α(۰, ۴) = ۵

همچنین در زیر کد برنامه محاسبه تابع آکرمان آمده است که از آن می‌توان رایانش‌پذیر بودن این تابع را نتیجه گرفت.

int function: ack(int m, int n)

{

if (n == 0)
{return m + 1; }
else if ((n > 0) AND  (m == 0)){return ack (n - 1, 1); }
else if ((n > 0) AND (m > 0)){return ack (n - 1, ack (n, m - 1)); }
else return n + 1;

}

تابع آکرمان را نیز می‌توان به صورت زیر تعریف کرد:

تابع آکرمان (The Ackermann function) [صورت دوم]
α۰(x ) =x + ۲;
αn+۱(۰) =۲;
αn+۱(x + ۱) =αn(αn+۱(x )).

رشد بسیار سریع و انفجاری این تابع نسبت به متغیرهای ورودی آن در جدول زیر نمایش داده است.

تابع آکرمان
رشد تابع آکرمان نسبت به متغیرهای وردوی آن (n و m)

• برخی ویژگی‌های تابع آکرمان

ویژگیاثبات
α(۱, m) = m +۲۱. داریم:
α(۱, ۰) = α(۰, ۱) = ۲
۲. فرض:
α(۱, m) = m + ۲
۳. پس:
α(۱, m+۱) = α(., m+۲) =
= m+۳ = (m +۱) +  ۲
α(۲, m) = ۲m +۳ 
m < α(n, m) 
α(n, m+۱) < α(n+۱, m) 

■ تابع آکرمان یک تابع نخستینی-بازگشت نیست.

اثبات اینکه تابع آکرمان یک تابع P.r نیست را می‌توان، از جمله، در فصل ۴ [George Tourlakis] یافت. درواقع، اینکه تابع آکرمان P.r نیست بر مبنای دو قضیه زیر است.

۱: رشد تابع آکرمان از هر تابع P.r سریع‌تر است.
۲: نمی‌توان از توابع آغازین (A۲ ،A۱ و A۳) و با کارزدن متناهی دو قاعده R۱ و R۲ تابع آکرمان را استخراج کرد.

اکنون که دانستیم تابعی هست که رایانش‌پذیر و نیز بازگشتی است و در عین حال P.r نیست، باید کلاس توابع P.r را به گردایه (کلاس) توابع بازگشتی (عام) گسترش دهیم. پیش از آن باید «کمینه سازی بی‌کران - Unbounded Minimalization» را معرفی کنیم.

■ کمینه سازی بی‌کران (Unbounded Minimalization)

فرض کنید g(x, y) یک تابع n+۱ متغیری (n≥۱) باشد. در این صورت کمینه سازی بی‌کران تابع g عبارت است از: تابع n متغیری f به قسمی که:

عملگر کمینه‌ساز بیکران - μ : f(x) = μy (g(x, y) = ۰).

عبارت سمت راست مساوی این‌گونه خوانده می‌شود: y به قسمی که g(x, y) معین باشد، و این y برای x کوچکترین yای باشد که داشته باشیم: g(x,y)=۰. آشکار است که در این تعریف، y وابسته به x است. اگر در تعریف بالا y را با نظیر آن در کمینه‌سازی ‌کراندار مقایسه کنیم خواهیم دید در اینجا y دارای کران بالا (k) نیست.

در کمینه‌سازی بیکران ممکن است برای برخی x، y یافت نشود و در این صورت تابع f نامعین است و داریم:

f(x) =
f(x) = μy (g(x, y) = ۰)اگد y وجود دارد:
↑وگرنه:

یعنی، f یک تابع جزئی خواهد بود.

☚: اگر f کامل باشد آنگاه می‌توان یک برنامه به یک زبان برنامه نویسی، به فرض برنامه ⓟμy g(x, y)، نوشت و (مقدار) y را یافت، که در این صورت این f رایانش‌پذیر خواهد بود.

کمینه‌سازی

ⓟμy: (x, y)

{

y ← Z(y);
while (g(x, y) ≠ 0)
{ y ← S(y)}
write (y)

}

☚: چرخه آزاد را در اینجا و چرخه کراندار را در اینجا ببینید.

☚: اگر f کامل نباشد، یعنی برای برخی x‌ نامعین باشد و y وجود نداشته باشد، آنگاه برنامه ⓟμy g(x, y) برای این x‌ها (فارغ از محدویت حافظه) از کار باز نخواهد ایستاد (پایان ناپذیر خواهد بود).

• مثال:

فرض کنید g(x, y) = g(x, y) = x+y. نیز فرض کنید:

 f(x) = f(x) = μy (g(x + y) = ۵).

f(x) =
f(۰)=۵, f(۱)=۴, f(۲)=۳,
f(۳)=۲, f(۴)=۱, f(۵)=۰		برای {۰, ۱, ۲, ۳, ۴, ۵}∋x.
↑برای {۰, ۱, ۲, ۳, ۴, ۵}∌x.

■ توابع بازگشتی (Recursive Function - r.c)

تعریف تابع بازگشتی به شیوه استقرایی:

تابع  f(x) یک تابع بازگشتی، با کوته نام r.c، (نیز نامیده به تابع بازگشتی کامل - Total Recursive) است اگر:

۱. یک تابع P.r باشد،

۲. بوسیله کمینه‌سازی بیکران (عملگر μ) از تابع بازگشتی از پیش تعریف شده g(x,y) به دست آمده باشد. به عبارت دیگر داشته باشیم:

 f(x) = μy (g(x, y) = ۰).

که در آن g یک تابع بازگشتی تعریف شده باشد.

۳. فقط توابعی بازگشتی هستند که از ۱ و ۲ به دست آمده باشند.

☚: همانطور که گفته شد حاصل عملگر μ می‌تواند یک تابع جزئی باشد. اما در تعریف توابع بازگشتی که در بالا آمده است، حاصل عملگر μ یک تابع (کامل) است. از این جهت گاهی با آوردن واژه "کامل" درون پرانتز این نکته یاد می‌شود.

☚: به صورت خلاصه تابع f(x,y) بازگشتی است اگر و فقط اگر:

  • f یک تابع P.r باشد،
  • اگر g بازگشتی باشد آنگاه تابع f تعریف شده در زیر نیز بازگشتی باشد:

f(x) = μi (g(x, i) = ۰ ∧  ∀j < i (g(x, y) ≠ ۰)

☚: بنا به تز چرچ داریم:

تابع بازگشتی ⇔ تابع رایانش‌پذیر

به عبارت دیگر:

بازگشتی ⇔ رایانش‌پذیری

رایانش‌پذیری و ‌بازگشتی

☚: تابعی که بازگشتی نیست را تابع رایانش‌ناپذیر می‌گوییم.

• توابع بازگشتی تحت سور کراندار↝ بسته هستند.

[مراد از سور کراندار، سوری است که دامنه متغیر آن محدود باشد.]

■ اثبات:

سور وجودی کراندار:

∃y<z R(x, z) را Q(x, z) می‌نامیم و می‌نویسیم:

Q(x, z+۱) ≡ Q(x, z) ∨ R(x, z).↜

سور عمومی کراندار:

∀y<z R(x, z) ≡ ~∃y<z ~R(x, z).↜

■ مجموعه رایانش‌پذیر (نیز بازگشتی - تصمیم‌پذیر)

گیریم A یک مجموعه باشد، آنگاه A را یک مجموعه بازگشتی (مجموعه تصمیم‌پذیر - مجموعه رایانش‌پذیر) گوییم اگر تابع مشخصه آن r.c باشد. مجموعه‌ای که تصمیم‌پذیر نیست را مجموعه تصمیم‌ناپذیر می‌گویند.

برای مثال مجموعه‌های ‌اعداد طبیعی↝، اعداد زوج و متناهی رایانش‌پذیر هستند.

χℕ = ۱.
χ∅ = ۰.

مجموعه‌های اعداد طبیعی و تهی را مجموعه‌های تصمیم‌پذیر ناچیز (Trivial - دم دستی - پیش‌پایی) می‌نامند.

■ مسئله تصمیم گیری (Decision problem)

فرض کنید D یک مجموعه باشد. آنگاه به پرسش «عضویت x دلخواه در D» یک مسئله تصمیم‌ گیری D می‌گویند. به پرسش از عضویت عنصر معین d در D یک مورد پرسش از مسئله D گفته می‌شود.

اگر D تصمیم‌پذیر باشد آنگاه تابع مشخصه آن رایانش‌پذیر است و مقدار این تابع برای هر x برابر ۰ یا ۱ خواهد بود. بنابراین هر مورد مسئله تصمیم‌ پذیر D همیشه دارای پاسخ رایانشی قطعی آری/نه خواهد بود.

■ رابطه رایانش‌پذیر (نیز بازگشتی - تصمیم‌پذیر)

گیریم R یک رابطه باشد، آنگاه R را یک رابطه بازگشتی (نیز رابطه تصمیم‌پذیر - رابطه رایانش‌پذیر) گوییم اگر تابع مشخصه آن r.c باشد.

■ جبر تصمیم‌پذیری (Algebra of decidability)

اگر A و B مجموعه‌های تصمیم‌پذیر  باشند، آنگاه مجموعه‌های زیر نیز تصمیم‌پذیر هستند.

۱. A;
۲. A ∩ B;
۳. A ∪ B;
۴. A / B.

اثبات:

۱. χA = sgn(χa) = ۱ ∸ χA ;
۲. χA∩B = χA × χB;
۳. χA∪B = sgn(χA  + χB);
۴. χA/B = χA ∩ B.

نیز، فرض کنید R(x) و Q(x) رابطه تصمیم‌پذیر nگانه باشند. آنگاه روابط زیر نیز تصمیم‌پذیر هستند.

۱. ~R(x);
۲. R(x) ⋁ Q(x);
۳. R (x) ∧ Q(x);
۴. R (x) / Q(x).

■ ویژگی غیر-زبانی (non-linguistic) توابع بازگشتی

ویژکی زبانی و غیر زبانی

در این بند توضیح خیلی کوتاه در باره ویژگی غیر-زبانی (non-linguistic) مفهوم بازگشی، یعنی آنچه در نقل قول↝ این قسمت آمده است، می‌آوریم.  [مراد از ویژگی‌های زبانی آن ویژگی‌های زبان‌های طبیعی است که آن‌ها را از سایر صورت‌های ارتباط یا بیان متمایز می‌کنند]↧.

1. <https://www.academia.edu/4416229/The_properties_of_Language>
2. Scholz, Barbara C., Francis Jeffry Pelletier, Geoffrey K. Pullum, and Ryan Nefdt, "Philosophy of Linguistics", The Stanford Encyclopedia of Philosophy (Spring 2022 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/spr2022/entries/linguistics/>.

بنا به اصل طرد شق ثالث در منطق کلاسیک می‌دانیم گزاره «حدس کولاتز درست است.» باید درست یا نادرست باشد. بنابراین، تابع F که در زیر تعریف شده است باید یک تابع رایانش پذیر باشد.

F = 
۱   اگر حدسن کولاتز درست است آنگاه:
۰ اگر حدس کولاتز درست نیست آنگاه:

اگر تابع F در بالا رایانش پذیر است پس باید یک روند کارامد (روند مکانیکی) وجود داشته باشد که آن را محاسبه کند. اما این روند مکانیکی چه است؟ پاسخ این است که در تابع F در بالا با ویژگی‌های زبان طبیعی (linguistic) توصیف شده است و می‌توان آن را به شیوه‌های دیگر نیز توصیف کرد. ما در این قسمت دیدیم رایانش ‌پذیری ویژگی ریاضی یک تابع (یعنی ویژگی بازگشتی بودن تابع) و نه ویژگی زبانی (linguistic) است. بنابراین همیشه، چه حدس کولاتز به نتیجه برسد و چه نرسد، تابع F در بالا رایانش پذیر است.

در اینجا مرور ما در بحث توابع بازگشتی پایان می‌یابد. در یادداشت‌های بعد بیشتر  در پی یافتن مسئله‌های رایانش‌ناپذیر، و ارائه متدولوژی برای شناخت و بازشناسی آنها، خواهیم بود.

منابع و ارجاعات

1- Davis, Martin, editor. The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.

این کتاب مجموعه‌ای از مقالات بنیادی در درباره (مسئله) تصمیم ناپذیری و حل ناشدنی است. که توسط مارتین دیویس ویرایش شده است. کتاب با مقاله برجسته گودل در سال ۱۹۳۱ (قضیه ناتمامیت) آغاز می‌شود. ویرایشگر کتاب مارتین دیویس (۲۰۲۳ - ۱۹۲۸) یک منطقدان، ریاضیدان و دانشمند کامپیوتر آمریکایی است. وی سهم قابل توجهی در زمینه‌های نظریه رایانش و منطق ریاضی داشت. او بیشتر به خاطر کارش روی پرسش دهم هیلبرت که منجر به قضیه MRDP می‌گردد، شناخته شده است.

MRDP <https://www.logicmatters.net/resources/pdfs/MRDP.pdf>
<http://www.scholarpedia.org/article/Matiyasevich_theorem>

2- Davis, Martin. The Universal Computer: The Road from Leibniz to Turing. CRC Press/Taylor & Francis Group, 2018.

3- Davis, Martin,  Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.

4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf

5- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.

6- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing.  (2011).

7- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)

8- George Tourlakis, Computability, Springer International Publishing. (2022.)

9- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. 2015.

10- Theory of Recursive Functions and Effective Computability. Journal article·1969·Feferman, Rogers·Mathematical Association of America.

11- Herbert B. Enderton An Introduction to Recursion Theory. Academic Press is an imprint of Elsevier (2011).

12. Scholz, Barbara C., Francis Jeffry Pelletier, Geoffrey K. Pullum, and Ryan Nefdt, "Philosophy of Linguistics", The Stanford Encyclopedia of Philosophy (Spring 2022 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/spr2022/entries/linguistics/>.

◄ توجه: