توابع بازگشتی نخستینی (Recursive Primitive Functions)
منطق و نظریه رایانش (۲)
درآمد به منطق
اولین قاعده شایسته در نوشتن، استفاده از واژگانی است که معنای آنها اشتباه گرفته نشود، و اگر خواننده معنی واژگان را نداند، بی نهایت بهتر است که بداند آنها را نمیداند.
چارلز سندرس پیرس, Ethics of Terminology, [73, p. 131]. Laine Ketner, Transactions of the Charles S. Peirce Society Vol. 17, No. 4 (Fall, 1981.)
این یادداشت به دستگاه «توابع بازگشتی نخستینی» میپردازد. یعنی توابعی که میتوانند توسط چرخههای کراندار (حلقه for) رایانش شوند. توابع بازگشتی نخستینی بر پایه سه تابع پیشینی «تابع صفر»، «تابع تالی» و «تابع افکنش» و دو قاعده «قاعده ترکیب» و «بازگشتی-نخستینی» گسترش مییابند. حاصل این گسترش زیرکلاس سره توابع رایانشپذیر است.
 منطق و نظریه رایانش (۲): توابع بازگشتی نخستینی
منطق و نظریه رایانش (۲): توابع بازگشتی نخستینی
≡
۱- مقدمه | ۱۹- قاعدههای جمع و ضرب کراندار (Bounded sum, bounded product rules) |
۲- یادآور | ۲۰- باقیمانده و خارج قسمت |
۳- یادداشت تاریخ | ۲۱- شمارش مقسوم علیه |
۴- تز چرج-تورینگ (Church–Turing thesis) | ۲۲- تابع چرخه |
۵- دستگاه توابع بازگشتی-نخستینی (Primitive Recursive Functions) | ۲۳- تابع ثابت |
۶- تابع بازگشتی-نخستینی (p.r) | ۲۴- تعریف و استدلال مبتنی بر مورد (Case-based definition and reasoning) |
۷- مجموعه بازگشتی-نخستینی (Primitive recursive sets) | ۲۵- تعداد مقسوم علیهها (Counting divisors) |
۸- رابطه بازگشتی-نخستینی (Primitive recursive relations) | ۲۶- اول بودن |
۹- تابع کاهش | ۲۷- کمینه سازی کراندار (Bounded Minimalization) |
۱۰- تابع جمع | ۲۸- جستجوی کراندار |
۱۱- تابع تفریق کوتاه شده (Truncated subtraction function) | ۲۹- nامین عدد اول |
۱۲- تابع قدر مطلق | ۳۰- محاسبه توان nامین فاکتور اول در تجزیه اعداد |
۱۳- تابع علامت | ۳۱- دنبالههای کد گذاری (Coding sequences) |
۱۴- رابطههای کوچکتر و تساوی | ۳۲- رایانشپذیری و توابع بازگشتی-نخستینی |
۱۵- تابع ضرب | ۳۳- یادآوری روش قطری کانتور (Diagonalization method) |
۱۶- تابع توان | ۳۴- چنین نیست که همه توابع رایانشپذیر P.r باشند. |
۱۷- تابع فاکتوریل | ۳۵- منابع و ارجاعات |
۱۸- توابع بیشینه و کمینه |
■ مقدمه
• بازگشت و تعریف بازگشتی را ببینید.
در نظریه رایانش، یک تابع بازگشتی-نخستینی تابعی است که میتواند توسط یک ماشین اندوختگانی رایانش شود، به قسمی که چرخههای این رایانش همگی چرخه کراندار باشند.
«تئوری توابع بازگشتی» (Recursive Functions theory) که اکنون «نظریه رایانش» (Theory of Computation) نامیده میشود، پاسخ دقیقی به چیستی یک الگوریتم است. در واقع، نظریه رایانش بخشی از منطق ریاضی است که در پی پیکربندی دقیق برای مفاهیم الگوریتم، روند مکانیکی (روند ماشینی) و توابع رایانشپذیر (نیز مجموعهها و رابطههای رایانشپذیر) و سرانجام ارائه متدولوژی برای بازشناختن آنچه رایانش پذیر نیست است. ما در این یادداشت و سه یادداشت بعد با جزئيات درخور به مرور این نظریه خواهیم پرداخت.
■ یادآور
☚: در این قسمت، همه نگاشتها [توابع (کامل) و توابع جزئی]، مگر خلاف آن گفته شده باشد، از مجموعه توانی اعداد طبیعی، یعنی ℕn برای n≥۱، در ℕ تعریف میشوند. برای مثال:
f۱ : ℕ۲ → ℕ: f(x۱, x۲) = ۲x۱ + x۲ + ۱.
و به طور کلی:
f(x) : ℕn → ℕ.
☚: مراد از x (یا x<..,k>) دنباله متغیرهای (x۱,...,xk) برای k≥۱ است. برای مثال دنباله متغیرهای (x۱,x۲,x۳).
■ یادداشت تاریخ
واژه الگوریتم (al-gorithm) برگرفته از نام ریاضیدان ایرانی خوارزمی (al-khwarizmi)، قرن نهم میلادی (دوم و سوم خورشیدی)، است. وی از جمله قواعد حساب اعداد (جمع، تفریق، ضرب و تقسیم اعشاری) و حل معادله درجه دوم (جبر و مقابله) را به شیوه خوارزمیک مدون و برای آنها برهان هندسی ارائه کرد. و البته اکنون بیشتر آدمیان از روش الگوریتمیک حل معادله ax۲+bx+c=۰ آگاه هستند.

در ادامه داستان، در قرن هفده با فیلسوف-ریاضیدان لایب نیتس روبرو میشویم که در اندیشه جبری کردن اندیشه (Algebraization of thought - Machinery of thought) بود. لایبنیتس ماشینی را اختراع کرد که عمل ضرب را انجام میداد. ماشین لایبنیتس، به نام حسابگر پلهای (stepped reckoner)، نهتنها میتوانست جمع و ضرب کند، بلکه میتوانست با دنبالهای از جمعهای پی در پی که حتی امروزه نیز استفاده میشود، عمل تقسیم و محاسبه ریشههای مربع را انجام دهد. سهم اصلی لایب نیتس نشان دادن برتری باینری بر نمایش اعشاری برای حسابگرهای مکانیکی بود. در کار لایب نیتس، نمایش نمادین مسائل با جستجوی راه حلهای الگوریتمی آنها ترکیب میشد. وی به راهحلهای الگوریتمی مسائل ریاضی و منطقی بهعنوان پارادایمهای حل مسئله مینگریست↧↧. در «یادداشت منطق» میتوان در این باره اندکی بیشتر یافت.
W. Sieg, Mechanical procedures and mathematical experience, Oxford Univ Press, 1994.
Martin Davis. The Road from Leibniz to Turing. CRC Press Taylor & Francis Group (2018.)

در فراز بعدی، در آغازین قرن بیستم (۱۹۰۰) دیوید هیلبرت (۱۸۶۲-۱۹۴۳) ریاضیدان نامی، در کنگره بینالمللی ریاضیدانان در پاریس، ۲۳ پرسش را به میان آورد و گفت «چه روشهایی، چه حقایق جدیدی در میدان گسترده و غنی اندیشه ریاضی در قرن پیش رو آشکار خواهد شد؟» تفصیل پرسش یکم (فرض پیوستار و اینکه بینهایتها یکسان نیستند) و پاسخ تاکنونی آن را میتوان در بحث مجموعهها (مقایسهپذیری، فرض پیوستار و بینهایتها) یافت. مورد توجه ما در اینجا فقط پرسش دهم است که در پاراگراف بعدی به آن خواهیم پرداخت.
موضوع پرسش دهم دیوید هیلبرت حل خوارزمیک معادلات سیاله (Diophantine equation) بود. پس ابتدا کوتاه معادله سیاله را یادآوری میکنیم. معادله سیاله (Diophantine equations) معادلهای است که در آن فقط از جمع، ضرب و توان و ثابتهای صحیح استفاده میشود و از باستان شناخته شده بودند. برای مثال x=۳ و y=۲ یک جواب معادله ۱۰x۲-y۲-۸۶=۰ است. حال آنکه معادله x۲-۲=۰ دارای جواب نیست.
• مسئله دهم هیلبرت:
آیا روش خوارزمیک برای محاسبه ریشه(های) معادلات سیاله هست؟↧
این پرسش در ۱۹۷۰، یعنی بیش از ۷۰ سال پس از ارائه فهرست پرسشهای هیلبرت، توسط یوری ماتیسویچ پاسخ خود را یافت، یعنی:
پرسشی بنیادی از مسئله دهم هیلبرت برخاست و آن اینکه: محاسبه کارآمد، نیز - روند مکانیکی (Effective calculability - Mechanical Processes) چیست؟ هیلبرت همچنین در ۱۹۲۸ پرسید:
«آیا الگوریتمی هست تا در مورد قابل استنتاج بودن فرمول داده شدهای در یک دستگاه استنتاجی از اصول موضوعه آن دستگاه با استفاده از قواعد استنتاج آن تصمیم بگیرد؟»
اکنون میدانیم پاسخ برای بعضی دستگاه استنتاجی چنین است. برای نمونه منطق گزارهای (فصلهای ۹ و ۱۰ کتابدرآمد به منطق)، منطق محمولات یک متغیری (Monadic predicate) و زیربخشهایی از منطق محمولات دو متغیری تصمیمپذیر هستند. (تمامیت روش درخت صدق و ناتمامیت گودل را در اینجا، اینجا و اینجا ببینید). اما بطور کلی چنین نیست و منطق محمولات تصمیمپذیر نیست↧. بنابراین پاسخ این پرسش نیز نه است. این پرسش اخیر به «مسئله تصمیمپذیری» (Entscheidungsproblem) شهرت دارد.
Alonzo Church (Apr., 1936). An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. pp. 345-363.
https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf
سرانجام پاسخ به پرسش «سرشت صوری الگوریتم - محاسبه کارآمد - چیست و مدل(های) نظری-اجرایی آنها چه میتوانند باشند؟» پاسخ یافت. پاسخ به قسمت اول پرسش نه چندان دیر با مدون کردن توابع بازگشتی سامان یافت:
هر توابع بازگشتی رایانشپذیر است.
☚: توابع بازگشتی (نظریه رایانش) موضوع اصلی این یادداشت و یادداشت بعد است.
پاسخ قسمت دوم پرسش تقریباً همزمان توسط آلونزو چرچ (۱۹۳۵-۶) و آلن تورینگ (۱۹۳۶-۷)↧ ارائه گردید.
■ تز چرج-تورینگ (Church–Turing thesis)
پاسخ آلونزو چرچ دستگاه صوری حساب لامبدا - λ-calculus و پاسخ تورینگ ماشینهای نظری تورینگ (Turing machines) بود. سپس با آنچه به تز چرج-تورینگ مشهور است پرسش معرفت شناسانه رایانشپذیری پاسخ درخور را یافت↧. یعنی:
هر تابع
محاسبه پذیر به شیوه چرچ (حساب لامبدا) به شیوه تورینگ (ماشینهای تورینگ) نیز محاسبه پذیر است
و هر تابع
محاسبه پذیر به شیوه تورینگ (ماشینهای تورینگ) به شیوه چرچ (حساب لامبدا) نیز
محاسبه پذیر است↜،
به عبارت دیگر:
هر تابع بازگشتی یک تابع محاسبه پذیر به شیوه چرچ (حساب لامبدا) است و هر تابع بازگشتی یک تابع محاسبه پذیر به شیوه تورینگ (ماشینهای تورینگ) است،
و سرانجام:
تز چرچ: (Church’s Thesis)
تابع بازگشتی ⇔ تابع رایانش پذیر،
به عبارت دیگر تابع:
f : ℕk→ℕ
بهطور کارآمد محاسبهپذیر (رایانشپذیر) است اگر و تنها اگر بازگشتی باشد.
■ دستگاه توابع بازگشتی-نخستینی (Primitive Recursive Functions)
توابع آمده در فهرست زیر، یعنی A۲ ،A۱ و A۳، را به عنوان توابع پیشینی بازگشتی-نخستینی در دستگاه توابع بازگشتی-نخستینی معرفی میکنیم.
| توابع پیشینی بازگشتی-نخستینی (Primitive recursive a priori functions) | |||||
A۱. تابع صفر (Zero function). | A۱: Z(x) = ۰ | ||||
| A۲. تابع تالی (Successor function). | A۲: S(x) = x + ۱ | ||||
| A۳. تابع افکنش (Projection function). خروجی تابع افکنش مقدار متغیر ورودی iام تابع است. در تعریف این تابع، k مشخص کننده تعداد متغیرهای ورودی تابع و i شماره متغیری ورودی است که مقدار آن خروجی تابع خواهد بود. تابع همانی، f(x)=x، نمونهای از تابع افکنش است: Prj<۱,۱>(x)=x. | A۳: π<i, k>(x۰, ..., xk) = xi; [۰≤i<≤k]. و در صورت معلوم بودن k فقط مینویسیم: | ||||
دو قاعده، R۱ و R۲، که در پی خواهند آمد قواعد گسترش توابع نخستیی-بازگشتی بر پایه توابع پیشینی A۲ ،A۱ و A۳ هستند. | |||||
R۱. قاعده ترکیب cmp.rl: فرض کنید f یک تابع m متغیری بازگشتی-نخستینی باشد. بعلاوه توابع g۱,...,gm هر یک تابع n متغیری بازگشتی-نخستینی باشند. در این صورت، تابع h که از ترکیب توابع g۱,...,gm در f به گونه زیر به دست میآید نیز بازگشتی-نخستینی است: h(x۱, ..., xn) = f(g۱(x۱, ..., xn), . . ., gm(x۱, ..., xn)) تابع h را تابع جانشینی g۱,...,gm در f مینامند. برای مثال وقی f دو متغیری است داریم: h(x, y) = f(g۱(x, y), g۲(x, y)). بنابراین، طبق قاعده R۱، با ترکیب تابع نخستینی f و توابع نخستینی giها میتوان یک تابع نخستینی بازگشتی جدید به دست آورد. | |||||
R۲. قاعده بازگشتی-نخستینی (pr.rl): فرض کنید k>۰ و g تابع k متغیری، H تابع k+۲ متغیری و f تابع k+۱ متغیری باشد، به قسمی که برای هر (x۰, ...,xk,)∈Nk و m∈ℕ داشته باشیم:
برای مثال وقی f دو متغیری است داریم:
a'۱: f(x, ۰) = g(x) وقتی f از کار زدن این قاعده به دست آمده باشد، میگویند تابع f بگونه بازگشتی نخستینی از توابع g و H به دست آمده است. به عبارت دیگر، در تعریف تابع f گام مبنایی (مقادیر آغازین) به وسیله تابع g و گام استقرایی (پرش استقرایی) توسط تابع H بیان میشوند. در تعریف بالا به x۱,...,xk پارامترهای بازگشتی گفته میشود. | |||||
■ تابع بازگشتی-نخستینی (p.r)
به هر تابع که از A۱، A۲ و A۳ و توسط قواعد R۱ یا R۲ (یا هر دو) به دست آید تابع بازگشتی-نخستینی (با کوته نام p.r) گفته میشود.
کلاس توابع p.r :
کلاس توابع بازگشتی-نخستینی کوچکترین کلاس همه آن توابع است به گونهای که این کلاس شامل A۱، A۲ و A۳ باشد و نیز تحت R۱ یا R۲ بسته باشد. [یک عمل تعریف شده در یک کلاس (یا مجموعه) بسته است اگر حاصل عمل خود عضوی از آن کلاس (یا مجموعه) باشد].
قالب کلی تابع بازگشتی-نخستینی ی f(x, S(y)) را میتوان بصورت زیر (موسوم به معادلات بازگشتی) نشان داد:
f(x, ۰) = g(x), f((x, S(y)) = h(x, y, S(x, y))
از تعریف توابع P.r برمیآید که کلاس توابع P.r شمارا (برشمردنی) است.
■ مجموعه بازگشتی-نخستینی (Primitive recursive sets)
گیریم A یک مجموعه باشد، آنگاه A را یک مجموعه بازگشتی-نخستینی (مجموعه تصمیم پذیر بازگشتی-نخستینی) گوییم اگر تابع مشخصه آن P.r باشد.
■ رابطه بازگشتی-نخستینی (Primitive recursive relations)
گیریم R یک رابطه باشد، آنگاه R را یک رابطه بازگشتی-نخستینی (نیز رابطه تصمیم پذیر بازگشتی-نخستینی) گوییم اگر تابع مشخصه آن بازگشتی-نخستینی باشد.
مثال:
فرض کنید l یک تابع دو متغیری باشد. تابع f را به قرار زیر تعریف میکنیم:
f(x, b) = l(x, ۰) + ۲l(x, ۱) + . . . + (b + ۱)l(x, b).
برای اینکه نشان دهیم تابع f یک تابع P.r است دو تابع g و H که P.r هستند را یافته و نشان میدهیم f از g و H با کارزدن قاعد R۲ به دست میآید.
تابع g را به قرار زیر تعریف میکنیم:
a'۱: g(x) = l(x, ۰).
برای تعریف H بنابر تعریف f میتوان نوشت:
f(x, b + ۱) =
= l(x, ۰) + ۲l(x, ۱) + . . . + (b + ۱)l(x, b) + (b + ۲)l(x, b +۱) =
= f(x, b) + (b + ۲)l(x, b +۱)
از طرفی، H باید در رابطه زیر صدق کند:
f(x, b + ۱) = H(x, b, f(x, b)).
بنابراین H به قرار زیر خواهد بود:
a'۲:H(x, b, y). = y + (b + ۲)l(x, b +۱)
■ تابع کاهش
نشان میدهیم تابع کاهش، D، (نیز موسوم به تابع پیشین - Decrease function - Predecessor function)، تعریف شده در زیر، P.r است.
| D(x) | = |  |
| D(۰) = D(۱) =۰ | ||
| D(x) = x - ۱ |
مینویسیم:
■ تابع جمع
نشان میدهیم تابع sum (جمع) P.r است.
مینویسیم:
■ تابع تفریق کوتاه شده (Truncated subtraction function)
نشان میدهیم تابع تفریق کوتاه شده، "∸"، که در زیر تعریف شده است، P.r است.
| x۱ ∸ x۲ | = |  |
| ۰ | x۱ < x۲ | |
| x۱ - x۲ | x۱ ≥ x۲ |
مینویسیم:
■ تابع علامت
تابع sgn(x) (متمم تابع علامت) یک تابع P.r است:
■ رابطههای کوچکتر و تساوی
رابطههای کوچکتری و تساوی با توجه به توابع مشخصه زیر P.r هستند:
χ=(x, y) = ۱ ∸ (sgn(x ∸ y) + sgn(y ∸ x))
■ تابع ضرب:
نشان میدهیم تابع ضرب بازگشتی نخستینی است.
مینویسیم:
| mul(x۱, S(x۲)) = |  |
| mul(x۱, ۰) = g(x۱) = Z(x۱) | |
| = H(x۱, x۲ , Sum (x۱, x۲)) = = sum(π<۱>, π<۳>)(x۱, x۲, mul(x۱, x۲)) |
■ تابع توان
تابع توان بازگشتی-نخستینی است:
■ تابع فاکتوریل
تابع فاکتوریل، !، بازگشتی-نخستینی است:
| fctrl(S(x۱)) = |  |
| fctrl(۰) = ۱ | |
| fctrl(۱) = ۱ | |
| mul(S(x۱), fctrl(x۱)) |
■ توابع بیشینه و کمینه
توابع min(x,y) و max(x,y) بازگشتی-نخستینی است:
min(x) =sgn(x ∸ y) × x + sgn(y ∸ x) × y
max(x) =sgn(x ∸ y) × x + sgn(y ∸ x) × y
■ قاعدههای جمع و ضرب کراندار (Bounded sum, bounded product rules)
دو قاعده جمع کراندار و ضرب کراندار که در پی میآیند موجب آسانی گسترش توابع و مجموعههای P.r میگردند. میتوان به آسانی نشان داد که این دو قاعده از A۱، A۲ و A۳ و توسط قواعد R۱ یا R۲، با توجه به توابعی که تاکنون گسرانده شدهاند، به آسانی قابل استنتاج هستند.
قاعده جمع کراندار
فرض کنید تابع f(x, y) یک تابع P.r باشد. در این صورت، تابع BndS که در زیر تعریف شده است و جمع کراندار نام دارد، یک تابع P.r است.
BndS(x, y) = 𝚺<i=۰, y>f(x, i) = f(x, ۰) + ... + f(x, y)
| BndS(x, S(y)) | = |  |
| BndS(x, ۰) = f(x, ۰) | ||
| BndS(x, y + ۱) = BndS(x, y) + f(x, y + ۱) |
قاعده ضرب کراندار
همچنین، فرض کنید تابع f(x, y) یک تابع P.r باشد. در این صورت، تابع BndP که در زیر تعریف شده است و ضرب کراندار نام دارد، یک تابع P.r است.
BndP(x, y) = Π<i=۰, y>f(x, i) = f(x, ۰) × ... × f(x, y)
یک تابع P.r است.
| BndP(x, S(y)) | = |  |
| BndP(x, ۰) = f(x, ۰) | ||
| BndP(x, y + ۱) = BndP(x, y) + f(x, y + ۱) |
■ باقیمانده و خارج قسمت
تابع باقیمانده (Remainder) تقسیم x بر y یک تابع P.r است:
تابع خارج قسمت (Quotient) تقسیم x بر y وقتی x|y یک تابع P.r است:
| quo(x, S(y)) | = |  |
| quo(x, ۰) = ۰ | ||
| quo(x, S(y)) = quo(x, y) + sgn(rmd(x, y)) |
■ شمارش مقسوم علیه
■ تابع چرخه
تابع چرخه [Function iteration] تعریف شده در زیر به شرط P.r بودن تابع BLoop یک تابع P.r است:
 |
| BLoop⚬(y) = y |
| BLoopS(x)(y) = BLoop(Boopx (y)) |
■ تابع ثابت
تابع ثابت، Cte(x۱)=c، یک تابع P.r است. تابع Cte با کارزدن (ترکیب) c بار تابع تالی روی تابع صفر تعریف میشود. یعنی:
Cte(x۱) = S⚬Cte(Z(x۱)
به عبارت دیگر:
Cte(x۱) = S(S(S . . . S(Z(x۱))))
■ تعریف و استدلال مبتنی بر مورد (Case-based definition and reasoning)
فرض کنید g۱,...,gm و R۱,...,Rm به ترتیب توابع n متغیری و رابطههای n گانه P.r باشند، آنگونه که برای a∈ℕn یک و فقط یکی از رابطههای R۱(a),...,Rm(a) برقرار باشد. در این صورت تابع f، تعریف شده در زیر، P.r است.
| f(a) | = |  | ||
| g۱(a) .. .. gm(a) | ... ... ... ... | اگر R۱(a) آنگاه: .. .. اگر Rm(a) آنگاه: | مورد ۱: .. .. مورد m: |
تابع f تعریف شده در بالا را میتوان به صورت زیر نوشت که آشکارا P.r است.
f(a) = [g۱(a) × sgn(χ۱(a))] + . . . + [gm(a) × sgn(χm(a))].
■ در بالا χi تابع مشخصه رابطه Ri است و sgn متمم تابع علامت است.
■ تعداد مقسوم علیهها (Counting divisors)
■ اول بودن
تابع اول بودن x یک تابع P.r است.
| prm(x) | = |  |
| ۱ | اگر x اول است آنگاه: | |
| ۰ | وگرنه: |
■ کمینه سازی کراندار - Bounded Minimalization
فرض کنید g(x, y) یک تابع n+۱ متغیری (n≥۱) باشد. در این صورت کمینه ساز کراندار (با کوته نام B.Min) تابع g عبارت است از تابع n متغیری f به قسمی که: g(x, y) معین باشد و اگر این y برای x و به ازای y≤k (برای k معین) کوچکترین yای باشد که داشته باشیم:
B.Min: g(x, y) = ۰.
برای مثال: در تابع تفریق کوتاهشده (x∸y): برای هر y کوچکتر یا مساوی x داریم x∸y=۰. به عبارت دیگر کمینه تابع دو متغیری تفریق کوتاهشده تابع یک متغیری f(x)=x است.

در زبان یونانی «μικρό» (میکرو) به معنی کوچک است. در نظریه رایانش μ نماد عملگر کمینهساز (Minimalization operator) است.
گیریم g(x) یک تابع باشد، آنگاه تابع f(x) را کمینه کراندار تابع g(x) گوییم اگر:
در تعریف بالا عبارت سمت راست این گونه خوانده میشود: کوچکترین i که کوچکتر یا مساوی k باشد و داشته باشیم g(x, i)=۰. به عبارت دیگر در تعریف بالا داریم:
[∀j < i (g(x, i) ≠ ۰].
عملگر μ و حلقه for
for (i = 0; i <= K; /* k ثابت */ i++) {. . .}
☚: چرخه کراندار را در اینجا ببینید.
• حاصل جمع ضرب کراندار
میتوان نشان داد↧ اگر تابع g در بالا یک تابع P.r باشد آنگاه تابع کمینهساز کراندار آن، یعنی f، نیز P.r خواهد بود. به عبارت دیگر: میتوان نوشت:
μ(z≤k)(g(x, z) = ۰) = 𝚺(i≤k)(Π (j≤i+۱)sgn(g(x, j)))
که در آن عبارت سمت راست یک تابع P.r است.
• سور کراندار↝ (Bounded quantification).
گیریم R(x, z) یک رابطه k +۱ گانه باشد. سور عمومی کراندار↝ را به قرار زیر تعریف میکنیم:
∀y≤z R(x, z) ≝ ∀y(y ≤ z ⊃ R(x, z),
و میتوان نوشت:
∀y≤z R(x, z) = Π(i=۰→y) χu(x, i).
بنابراین، اگر p.r R(z, x) باشد آنگاه سور عمومی کراندار آن نیز p.r است.
به همین ترتیب، سور وجودی کراندار↝ را به قرار زیر تعریف میکنیم:
∃y≤z R(x, z) ≝ ∃y(y ≤ z ∧ R(x, z),
و میتوان نوشت:
∃y≤z R(x, z) = sgn[⅀(i=۰→y) χu(x, i)].
بنابراین، اگر p.r R(x, z) باشد آنگاه سور وجودی کراندار آن نیز p.r است.
■ جستجوی کراندار
کمینهسازی آن گونه که در بالا گفته شد را گاهی جستجوی کراندار (Bounded Search) مینامند و به شیوه زیر تعریف میکنند:
| μz ≤ y[f(x, z)=۰] | = |  |
| μz ≤ y | اگر f(x, z)=۰ آنگاه: | |
| y + ۱ | وگرنه: |
از این جهت به μ عملگر جستجو (Search operator) نیز میگویند.
■ nامین عدد اول
■ محاسبه توان nامین فاکتور اول در تجزیه اعداد
تابع ep(x, n): محاسبه توان nامین فاکتور اول در تجزیه x به عوامل اول یک تابع P.r است.
از حساب میدانیم هر عدد طبیعی بزرگتر از ۱ را میتوان بطور یکتا به عوامل اول تجزیه کرد. برای مثال:
[۱= ۲۰,۱= ۳۰ , ...]
۴=۲۲,
۷ = ۷۱,
۶۶۰۰ = ۲۳۳۱۵۲۱۱۱
اکنون تابع ep(x, n) را به صورت زیر تعریف میکنیم:
| ep(x, n) | = |  |
| k | اگر x, n>۰ است آنگاه k توان nامین عدد اول در تجزیه x به عوامل اول است | |
| ۰ | اگر x=۰ ⋁ n=۰ آنگاه |
و در زیر نشان میدهیم که ep(x, n) یک تابع P.r است.
■ دنبالههای کد گذاری (Coding sequences)
فرض کنید p۱,...,pn به ترتیب دنباله n عدد اول آغازین باشند، نیز فرض کنید s=(a۱,...,an) دنباله متناهی اعداد طبیعی باشد. دنباله s را میتوان با (توجه به بند بالا) به گونه زیر به صورت کد درآورد (کدگذاری کرد):

c = pow(p۱, a۱+۱) × pow(p۲, a۲+۱) × . . . × pow(pn, an+۱)
برای مثال دنباله s۱=(۳, ۱, ۲, ۱) را در نظر بگیرید. میتوان نوشت:
(۳, ۱, ۲, ۱) ↔ ۶۶۰۰ = ۲۳۳۱۵۲۱۱۱
(۳, ۱, ۲, ۱) ↔ ۶۶۰۰ = ۲۳۳۱۵۲۱۱۱۱۷۰۱۱۰
اکنون فرض کنید عدد ۶۶۰۰ داده شده است و میخواهیم طول دنباله s۱ را محاسبه کنیم. برای این کار کافی است کوچکترین توان عامل اول که از آن کوچکتر نباشد را به گونهای که در زیر آمده بیابیم:
طول c =µz<c (ep(c, z+۱) = ۰)
☚: برای مثال بیشتر «شمارایی مجموعه فرمولها» را ببینید.
عنصر iام دنبالهی تجزیه عدد c به عوامل را میتوان به شیوه زیر یافت:
NthF(c) = ep(c, i) ∸ ۱
• شمارگذاری گودل (Gödel Numbering)
☚: ابتدا «شماره گذاری گودل» در اینجا و اینجا را ببینید.
فرض کنید <x۰,...,xn> دنباله اعداد طبیعی باشد. با توجه به آنچه در دنباله کدکذاری آمده است، تابع ۱:۱ GN، که به شمارگذاری گودل معروف است، در زیر تعریف شدنی است:
Nn+۱→
ℕ: GN(<x۰,...,xn>) =  .
.
که در آن p۰,...,pn به ترتیب n+۱ عدد اول آغازین هستند.
■ رایانشپذیری و توابع بازگشتی-نخستینی
در یادداشتهای پیشین «روند منطق مدرن، الگوریتم، محاسبه و تصمیم» درباره الگوریتم، رایانشپذیری، تصمیم پذیری و مدل رایانشی شرح و تفصیل آمده است. میتوان نشان داد توابع آغازین (A۱، A۲ و A۳) رایانش پذیر هستند. نیز دو قاعده R۱ و R۲ سرایت دهنده رایانشپذیری هستند. پس هر تابع P.r رایانشپذیر است. [این را به آسانی نیز میتوان با استقرای روی تعداد گامها به کار رفته در استخراج توابع P.r نشان داد.] اما برعکس آن چطور؟ یعنی:
آیا هر تابع رایانش پذیر P.r است؟ پاسخ به طور قطعی نه است.
یعنی، حداقل یک تابع رایانش پذیر وجود دارد که بازگشتی-نخستینی نیست.
برای نشان دادن اینکه تابعی وجود دارد که رایانشپذیر است ولی P.r نیست از روش برهان قطری کانتور استفاده میکنیم. پیش از این به خود این روش را مرور میکنیم.
■ یادآوری روش قطری کانتور (Diagonalization method)
در یادآور نظریه مجموعهها برای اثبات ناشمارایی مجموعه اعداد حقیقی از روش موسوم به برهان قطری کانتور↝ سود جستیم. در آنجا نشان داده شد در هر برشمارش مجموعه اعداد حقیقی عضوی از اعداد حقیقی هست که در این برشمارش نیست، پس مجموعه اعداد حقیقی شمارش پذیر نیست.
مورد بالا فقط یکی از موردهای روش قطری است. ایده زیربنایی این روش در حالتهای گوناگون قابل پیاده سازی است و از جمله در اثبات بسیاری از نتایج در نظریه رایانش، به ویژه در رایانش ناپذیری توابع، مجموعهها و رابطهها، دارای نقش مرکزی است.
برای توضیح و روش کارزدن این روش فرض کنید کلاس توابع F (از ℕ در ℕ) برشمردنی و دارای ویژگی P هستند. بنابراین میتوان نوشت:
<F>: f۰, f۱, f۲, . . .
برشمارش <F> را میتوان در یک ماتریس (با تعداد سطر و ستون نامتناهی) همراه با برشمارش مقادیر متغیر x مطابق زیر نشان داد:
| برشمارش <F> | |||||
| fn(x) | ۰ | ۱ | . . . | n | . . . |
| f۰ | f۰(۰) | f۰(۱) | . . . | f۰(n) | . . . |
| f۱ | f۱(۰) | f۱(۱) | . . . | f۱(n) | . . . |
| . . . | . . . | . . . | . . . |
. . . |
. . . |
| fn | fn(۰) | fn(۱) | . . . | fn(n) | . . . |
| . . . |
. . . |
. . . |
. . . |
. . . |
. . . |
دنباله عناصر قطری ماتریس بالا را در زیر برمیشمریم:
f۰(۰), f۱(۱), . . . ,fn(n), . . .
اکنون تابع g (از ℕ در ℕ) را گونهای تعریف میکنیم تا بطور یکنوا و صریح عناصر قطری در بالا را به دنباله زیر برگرداند:
g(۰), g(۱), g(۲), . . .
به قسمی که برای هر n مقدار fn(n) از g(n) متفاوت باشد. در انتخاب تابع g(n) آزاد هستیم و فقط کافی است متفاوت از fn(n) باشد. در صورت وجود چنین تابعی آنگاه ثابت میشود که تابعی، یعنی g، هست که در کلاس F نیست، یعنی ویژگی P را ندارد.
■ چنین نیست همه توابع رایانشپذیر، توابع بازگشتی-نخستینی باشند↝.
اثبات:
از آنجا که کلاس توابع P.r شمارا است پس میتوان آنها را برشمرد. یعنی:
Φ۰, Φ۱, . . ., Φn-۱, Φn, Φn+۱, . . .
در ماتریس پایین (با تعداد سطر و ستون نامتناهی) برشمارش بالا همراه با برشمارش مقادیر متغیر x نشان داده شده است:
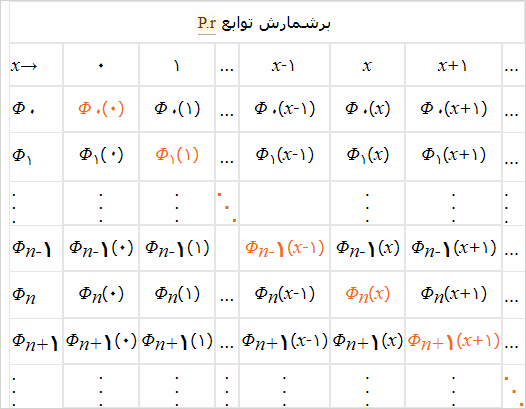
تابع U را برای n معین به قرار زیر تعریف میکنیم:
U(n, x) = Φn(x) .
اکنون تابع F را برحسب تابع تعریف شده U به قرار زیر تعریف میکنیم:
F(x) = U(x, x) + ۱.
(آشکار است که F باید P.r باشد.)
نشان میدهیم تابع F یک تابع P.r نیست.
/* Program Diagonalize */
F(x)
{
write (U(x, x) + ۱)
halt
}
برای اثبات فرض میکنیم F یک تابع P.r باشد. بنابراین و با توجه به تعریفِ Φn(x)، باید عدد n باشد که تحت F دارای تصویر Φn(x) در کلاس توابع P.r باشد. بنابراین میتوان نوشت:
(∀x)[F(x) = Φn(x) = U(n , x)].
رابطه بالا به ویژه برای x = n نیز برقرار است. پس:
F(n) = U(n, n).
اما بنابر تعریف داریم:
F(n) = U(n, n) + ۱.
که این یک تناقض است و بنابراین F یک تابع P.r نیست.
به عبارت دیگر، اگر F یک تابع P.r باشد F باید همان U باشد. در این صورت:
F(n) = U(n, n)
⇓
U(n, n) = U(n, n) +۱
⇓
۰ = ۱
در اینجا مرور ما در بحث توابع بازگشتی-نخستینی تمام میشود. در یادداشت بعد در پی یافتن موردی از تابع F در بالا خواهیم شد و اینکه چگونه با گسترش نخستینیها به بازگشتیها برسیم.
منابع و ارجاعات
1- Davis, Martin, editor.
The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.
این کتاب مجموعهای از مقالات بنیادی در درباره (مسئله) تصمیم ناپذیری و حل ناشدنی است. که توسط مارتین دیویس ویرایش شده است. کتاب با مقاله برجسته گودل در سال ۱۹۳۱ (قضیه ناتمامیت) آغاز میشود. ویرایشگر کتاب مارتین دیویس (۲۰۲۳ - ۱۹۲۸) یک منطقدان، ریاضیدان و دانشمند کامپیوتر آمریکایی است. وی سهم قابل توجهی در زمینههای نظریه رایانش و منطق ریاضی داشت. او بیشتر به خاطر کارش روی پرسش دهم هیلبرت که منجر به قضیه MRDP میگردد، شناخته شده است.
MRDP <https://www.logicmatters.net/resources/pdfs/MRDP.pdf>
<http://www.scholarpedia.org/article/Matiyasevich_theorem>
2- Davis, Martin. The Universal Computer: The Road from Leibniz to
Turing. CRC Press/Taylor & Francis Group, 2018.
3- Davis, Martin, Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.
4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf
5- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.
6- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing. (2011).
7- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)
8- George Tourlakis, Computability, Springer International Publishing. 2022.
9- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. 2015.
10- Hartley Rogers, Jr· Theory of Recursive Functions and Effective Computability. The MIT Press; Fifth Printing edition (April 22, 1987).
• در یادآور مجموعهها یادداشت مجموعهها و تعریف بازگشتی را ببینید.

