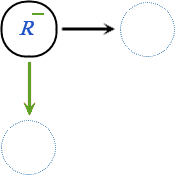
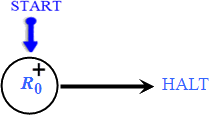
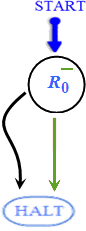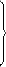• مثال ۴ (ماشین ابدی)
ماشین اندوختگانی این مثال که در زیر آمده است هرگز از کار بازنمیایستد (.مسئله توقف را ببینید.)
L1: R0- → L0, L2
L2: HALT
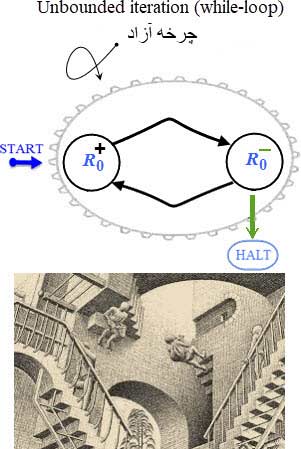
• مثال ۵ - ماشین واریز
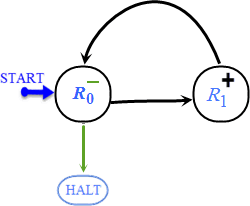
• مثال ۶ - ماشین جمع
ماشین این مثال دارای سه رجیستر R1، R0 و R2 است. این ماشین حاصل جمع مقادیر آغازین موجود در رجسیترهای R1 و R2 را در R0 ذخیره میکند. به عبارت دیگر، این ماشین همارز تابع f بقرار زیر است:
f : ℕ۲ → ℕ; f(x, y) = x + y.

• مثال ۷ - ماشین ضرب صحیح
فرض کنید تابع f به قرار زیر باشد:
f : ℕ۲ → ℕ; f(x, y) = x × y.
ماشین این مثال مقدار تابع f را برای مقادیر ورودیهای (مقدار متغیرها) آن، یعنی x و y، در رجیستر R0 برمیگرداند
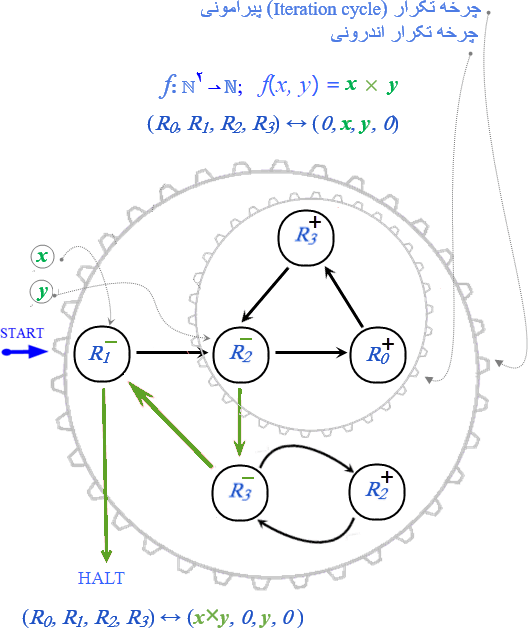
در این ماشین:
۱- در پیکربندی آغازین ورودیهای تابع، یعنی x و y، بترتیب در R1 و R2 ذخیره شدهاند و مقدار R0 و نیز R3 صفر فرض شده است.
۲- ماشین تابع f، یعنی ضرب x در y، را در دو چرخه تکرار (چرخه بیرونی و چرخه درونی) محاسبه میکند. این محاسبه با کاهش ضرب به جمع یعنی:

انجام میشود.
۳- چرخه بیرونی: در هر دور این چرخهی تکرار یک واحد از R1، که مقدار آغازین آن x است تا زمانی که مقدار آن صفر نشده کاسته میشود.
۴- چرخه درونی: در هر دور این چرخهی تکرار، به ازای هر دور چرخه بیرونی یک واحد از R1 تازمانی که صفر نشده کاسته شده و یک واحد به R0 و R3 افزوده میشود.
۴- در پایان دور اول این چرخه به مقدار R0 (که در پایان دور اول y است) مقدار y افزوده شده و R3 دارای مقدار y میگردد (مقدار y برای دور بعدی در R3 ذخیره میشود).
۵- در خروج از چرخه درونی مقدار R3 که y است در R2 که اکنون صفر است واریز و R3 صفر میشود.
• مثال ۸ - ماشین تفریق کوتاه شده
ماشین این مثال تابع زیر است:
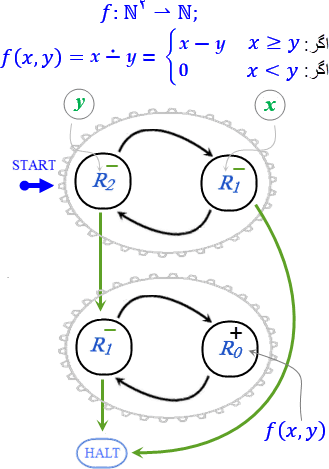
در پایان اجرای برنامه مقدار تابع به ازای مقادیر ورودیهای آن (مقدار متغیرها)، یعنی x و y، در رجیستر R0 ذخیره میشود.
• مثال ۹ - ماشین تقسیم صحیح (تابع کامل)
ماشین این مثال تابع (کامل) زیر است:
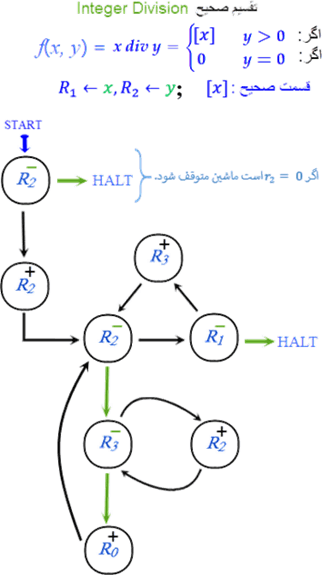
میتوان دید که در پایان کار این ماشین باقیمانده، در صورت ممکن بودن عمل تقسیم، در R۳ ذخیره شده است.
در پایان اجرای برنامه مقدار تابع به ازای مقادیر ورودیهای آن (مقدار متغیرها)، یعنی x و y، در رجیستر R0 ذخیره میشود.
| قطعه کد زیر برنامه ماشین این مثال، یعنی تقسیم صحیح، است. |
| L0: if (r[2]> 0) { r[2]--;
goto L1; } else goto L2; L1: if (r[1] > 0) { r[1]--; goto L0; } else goto HALT; L2: if (r[1] > 0) { r[1]--; goto L3; } else goto HALT; L3: r[0]++; goto L1; HALT: |
• مثال ۹.۱ - ماشین تقسیم صحیح (تابع جزئی)
ماشین این مثال تابع جزئی زیر است:
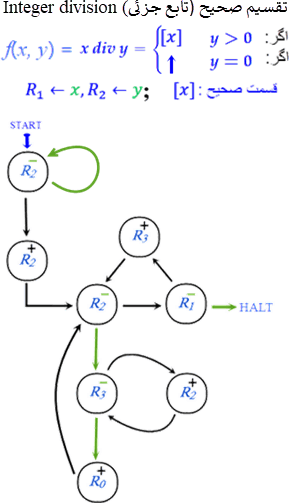
توجه داشته باشید که در این ماشین فقط وقتی که مقسوم علیه بزرگتر از صفر باشد، خارج قسمت محاسبه و در R۳ ذخیره میگردد. در غیر این صورت، ماشین به حالت نامعین (چرخه تکرار نامتناهی) انتقال خواهد یافت. به این توابع جزئی، که ممکن است برای برخی مقادیر ورودی نامعین باشند و ماشینهای اندوختگانی متناظر آنها برای این مقادیر پایان ناپذیر (نامعین) شوند، توابع رایانش پذیر جزئی (Partial computable functions) میگویند.
• مثال ۱۰ - ماشین افکنش (تصویر) - projection function
ماشین این مثال تابع زیر است:
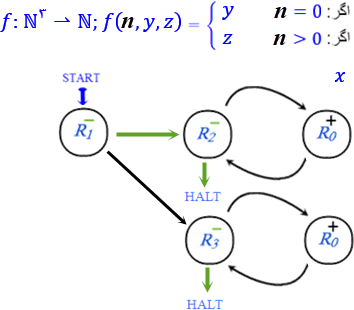
در پایان اجرای برنامه مقدار تابع به ازای مقادیر ورودیهای آن (مقدار متغیرها)، یعنی n و z ،y در رجیستر R0 ذخیره میشود.