درآمد به نظریه مجموعهها
نظریه بنداشتی (اصل موضوعی) مجموعهها
درآمد به منطق و رایانش
نظریه مجموعهها آن شاخه از ریاضیات است که وظیفهاش کاوش ریاضیوار مفاهیم بنیادین "عدد"، "ترتیب" و "تابع" و لحاظ داشتنشان بهصورت ساده و بکر است و بدینوسیله گستراندن مبانی منطقی همه حساب و آنالیز؛ و ازاینقرار مؤلفهای ناگزیر برای همه دانش ریاضی. . . . از یکسو، به خاطر اجتناب از هر تناقض، باید این اصول را بهاندازه کافی محدود . . . از دیگر سو بهاندازه کافی گسترده تا هر آنچه از این نظریه ارزشمند است باقی. ارنست زیملو - ↧
⦁ Ernst Zermelo" Collected Works/Gesammelte Werke: Volume I/Band I - Set Theory", 2010; Springer.
۱- در «آن سوی آینهها» | ۶- ■ مجموعه و عضویت |
۲- کتابخانه راسل | ۷- نظریه مجموعهها |
۳- پارادوکس دروغگو | ۸- زنجیرههای عضویتی کاهنده بیپایان |
۴- مجموعه چیست؟ | ۹- کلاسها و مجموعهها |
۵- زندگینامه جرج کانتور | ۱۰- کلاس و مجموعه در NBG |
■ در «آن سوی آینهها↝»
مجموعه چیست؟
What is a set?
جرج کانتور بنیانگذار نظریه مجموعهها گفت، یک مجموعه گردآمدهای از چیزهای معین و قابل تمیز در شهود و خرد است که همچون یک کل درک گردد.
نظریه مجموعهها
Set Theory
مجموعهها و درواقع نظریه مجموعهها (یا بگونه خاصتر نظریه مجموعههای بینهایت) یک دستگاه استنتاجی است. ریاضیدانان با چندین رهیافت این نظریه را بیان میکنند. ازجمله، نظریه طبیعی مجموعهها که در آن بهرهوری از زبان طبیعی حداکثری است و گرفتار ناسازگاری. اما بیان گوهری آن توسط دستگاه اصل موضوعی (دستگاه صوری)، ازجمله دستگاه موسوم به زیملو-فرانکل با کوته واژه ZF و دستگاه موسوم به نویمان-برنیز-گودل با کوته واژه NBG است.
عضویت
Membership
در نظریه مجموعهها ما دارای مفهوم جدید و مستقل عضو یا عنصر نیستیم؛ آنچه هست رابطه در مجموعه بودن (یا عضویت) بین مجموعهها است. به عبارت دیگر، در نظریه مجموعه، مراد از A∈B برقراری رابطه عضویت مجموعه A با مجموعه B است.


هامپتی دامپتی همچون عاقل اندر نادان گفت: «وقتی واژهای را بکار میگیرم معنیاش آن چیزی است که من برایش انتخاب میکنم - نه بیشتر و نه کمتر.»
آلیس گفت: «اما مسئله این است که چگونه ممکن است واژهها را با این همه معنی ساخت.»
هامپتی دامپتی گفت: «مسئله این است که چه کسی اینجا ارباب است ـ مسئله فقط همین است.» — لوئیس کارول، آنسوی آینهها
■ داستانک کتابخانه راسل
کتابخانه راسل
جایی نه چندان دور کتابخانهای سرشار از کتاب بود. در این کتابخانه هر کتاب دارای جلدی بود که روی آن عنوان کتاب آمده بود و همه صفحههای آن دارای متن بود و بعلاوه هر کتاب جدید نیز باید چنین میبود. در متن بعضی از کتابها به عنوان خود کتاب یک بار یا بیشتر اشاره شده و در متن بعضی به عنوان کتاب هرگز اشاره نشده بود. مدیر کتابخانه در تدارک تهیه کتابی با عنوان «فهرست ویژگان» برای کتابخانه بود، به قسمی که در آن فهرست، نام آن کتابهایی از کتابخانه آمده باشد که در متن آنها به عنوان آن کتاب اشاره نشده باشد. با شخصی و با مبلغ بسیار بالا قرارداد نوشتن و آماده کردن این کتاب بسته شد. این فرد پس از صرف مدت زمان طولانی و همراه با کار با دقت، فهرست مورد نظر را آماده میکند. هنگام تسویه حساب، مدیر کتابخانه از فرد طرف قرارداد درباره عنوان کتاب جدید کتابخانه میپرسد: ازآنجاکه این کتاب خود کتابی از کتابخانه و دارای متن و عنوان است، آیا در متن، عنوان آن آمده است؟ فرد طرف قرارداد درمانده بود چه باید کند و چه پاسخ دهد. اگر عنوان این کتاب را به متن آن بیافزاید آنگاه دیگر این کتاب «فهرست ویژگان» نبود؛ اگر عنوان این کتاب را به متن آن نیفزاید بازهم این کتاب «فهرست ویژگان» نبود. و چنین بود که مدیر کتابخانه از پرداخت مبلغ قرارداد سرباز میزد. بهعبارتدیگر، کتاب تحویلی «فهرست ویژگان» است اگر و فقط اگر «فهرست ویژگان» نیست➥.
برگرفته از:
• Jenkyns T. Stephenson . B. Fundamentals of Discrete Math for Computer Science. Springer. 2013.
■ پارادوکس دروغگو


پارادوکس دروغگو / خود-مرجع (Liar paradox / self-reference)
■ مجموعه چیست؟
جرج کانتور بنیانگذار نظریه مجموعهها گفت، یک مجموعه گردآمدهای از چیزهای معین و قابل تمیز در شهود و خرد است که همچون یک کل درک گردد. این قسمت نگاه نخستین به عناصر بنیادین ریاضی همچون مجموعه، عضویت، کلاس و رهیافتها در نظریه مجموعهها است؛ همچنین نگاه خیلی کوتاه است به نظریه کتگوری، که از جمله در پی پیافکندن زبانی جهانی برای همه ریاضی است. ناگفته نماند نظریه مجموعهها هماکنون همچون زبان مشترک برای عمده ریاضیات (ریاضیات کلاسیک) و نیز دانش کامپیوتر بکار است.
 ریاضی دانشی است که کسی روزی روزگاری شاید در یونان آن را با اثبات گزارههایی همچون برای هر چیزی یا برای بعضی چیز آسوده از آنکه آنها چه هستند بنیاد نهاد. http://khccsc.ir/logic/copi/ch11/ch11sec1_2_3.htm#alfred_north_whitehead_biog
ریاضی دانشی است که کسی روزی روزگاری شاید در یونان آن را با اثبات گزارههایی همچون برای هر چیزی یا برای بعضی چیز آسوده از آنکه آنها چه هستند بنیاد نهاد. http://khccsc.ir/logic/copi/ch11/ch11sec1_2_3.htm#alfred_north_whitehead_biog ازجمله ویژگی درخشان کار کانتور همانا بیان دقیق انگارههای بینهایت و بینهایتها است و اینکه گردایههای با بینهایت و بیشتر از بینهایت عضو به همان اندازه گردایههای با تعداد عناصر محدود شهودیاند و عجیب آنکه تعداد بیکرانهها از کراندارها بیشتر نیز است و برای هر بینهایت به تعدار بینهایت بینهایت بزرگتر نیز هست. پیش از کانتور انگاره بینهایت مبهم، خیالانگیز و افسونگر مینمود. ریاضیدانان و فیلسوفان از باستان کموبیش درگیر انگاره بینهایت بودند. در ادامه این یادآور با بینهایت و بینهایتها (شمارش و رتبهبندی بینهایتها) مقابل خواهیم نشست.
■ زندگینامه جرج کانتور:
گئورگ کانتور Georg Cantor (۱۸۵۴–۱۹۱۸)

کانتور (ریاضیدان آلمانی)
در سال ۱۸۵۴میلادی در سنت پترزبورگ روسیه پا به جهان گشود. پدرش یک بازرگان موفق و مادرش یک هنرمند بود.
پدر و مادر میخواستند وی یک مهندس شود. اما، خیلی زود آشکار شد او چندان مناسب این کار نیست و گرایش وی به ریاضی است.
کانتور ریاضی را ابتدا در دانشگاه زوریخ و سپس در دانشگاه برلین با بهره از استادان بنامی همچون وایرشتراس،
کرونکر و
کومر
پیگرفت.
وی بنیانگذار نظریه مجموعهها یا خاصتر نظریه مجموعههای نامتناهی است. انگاره نامتناهی (بینهایت) بحثی فریبنده است که بهآسانی منجر به پارادوکسهایی همچون پارادوکسها زنو الیایی میگردد. ازاینجهت، ترجیح ریاضیدانان تا زمان کانتور این بود تا بجای سخن از بینهایتهای "تمام" (مانند گردآمده همه اعداد) از بینهایتهای "بالقوه" (مثلاً، "هر عدد بزرگتر از یک" یا "بزرگترین عدد صحیح") سخن بگویند.
از گاوس ریاضیدان نامی در ۱۸۳۱ نقل است که گفت: "من به کاربرد مقدار بینهایت همچون چیزی "تمام"، که هرگز در ریاضی قابلقبول نیست، معترضم. بینهایت فقط یک روش سخن گفتن است و معنی آن فقط بودن یک حد است . . .."
البته بهاحتمال، گاوس در اینجا درباره مجموعههای نامتناهی نمیاندیشیده. مراد وی، کاربرد بینهایت، بهعنوان یک مقدار، در محاسبات است. بااینحال، در این نقلقول حضور یک سوءظن همگانی نسبت به بینهایت مشاهده شدنی است. کانتور اولین کسی بود که با مجموعههای بینهایت مواجه شد، آنها را حساب و مقایسه کرد؛ چیزی که اکنون ما در ریاضی همچون یک روند معمول بکار میبریم.
اولین مقاله کانتور درباره مجموعههای نامتناهی سی روز مانده به پایان سیسالگی وی منتشر شد. این مقاله چندان به ارکان ریاضی زمان خوش نیامد و موجب شد بسیاری ریاضیدانان به ویژه کرونکر آشکارا نگاه خصمانه به وی داشته باشند. ولی زمانه زود ارزش کار سترگ وی را دریافت. وی در ۱۸۶۹ بهعنوان رئیس انجمن ریاضی آلمان برگزیده و تا بازنشستگی در ۱۹۱۳ به همین سمت باقی ماند. وی در ۱۹۱۸ رخت از جهان بربست.
■ مجموعه و عضویت
داستان را از فرد معینی بنام پرویز آغاز کنیم که هرروز صبح فرزند خود را از مسیر مشخص به مدرسه میرساند. وی در راه مدرسه هرروز، کموبیش، چیزهای معینی، مانند تابلوی یک دندانپزشک، یک کیوسک مطبوعاتی، ماشین پارک شده مدیر مدرسه, خدمتگزار مدرسه، باجه تلفن و مانند آنها را میبیند. وی میتواند به همه این چیزها و فارغ از چیستی مستقل آنه (بهعبارتدیگر به صرف این باهم شدگی) یک نام نسبت دهد و ازآنپس با این نام از همه آنها یاد کند. فرض کنیم نام انتخابی وی "م۱" باشد. اکنون میگوییم م۱ یک مجموعه (یک باهم شدگی) است. کانتور گفت « م۱ باید همچون یک کل درک گردد»، به دیگر سخن و در دامنه سخن مجموعهها، چیستی م۱ چیستی همه گردآمدهها (تابلوی یک دندانپزشک، یک کیوسک مطبوعاتی، . . .) است. نیز به وارون، چیستی همه گردآمدهه (تابلوی یک دندانپزشک، یک کیوسک مطبوعاتی و ....) چیستی م۱ است.
پرویز ممکن است مجموعههای (باهم شدگیهای) دیگری را در ذهن خود داشته باشد یا بسازد. فرض کنیم یکی از آنها م۲ باشد. وی ممکن است مجموعهای از باهم شدگی م۱ و م۲ بسازد و آن را م۳ بنامد. اکنون میپرسیم رابطه م۱ با م۳ چیست؟ میتوان گفت هر سه مجموعهاند و البته این یک همانگویی بیش نیست (و چارهای هم نیست زیرا فعلاً انگارهای جز مجموعه بودن نداریم.) اینجاست که انگاره بنیادین دوم، یعنی رابطه در مجموعه بودن بین مجموعهها، پای به میدان سخن میگذارد. بنابراین پاسخ پرسش بهقرار «م۱ در م۳ است» خواهد بود. رابطه در مجموعه بودن (تعلق) را به صورتهای «م۱ عضو م۳ است»، «م۱ عنصر م۳ است»، «م۱ متعلق به م۳ است» یا «م۳ ∈ م۱» نیز مینویسند. همینطور، این رابطه بین م۲ و م۳ نیز برقرار است و میتوان نوشت: م۱ و م۲ اعضای م۳ هستند.
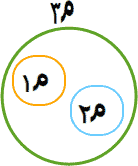
مهم است توجه داشته باشیم در نظریه مجموعهها مراد از عضو یا عنصر یک مجموعه، مجموعهای است که در رابطه "در مجموعه بودن" (یا "عضویت") با آن مجموعه است.
در نوشتهه عبارتهایی کموبیش مثل "فرض کنید ∑ یک مجموعه باشد ..." بسیار دیده میشود. در این موارد، اول و مهمترین چیز این است که قرار است عناصری (مجموعههایی) در میدان بحث بیایند که ازجمله عضو ∑، یعنی عضو یک مجموعه، خواهند بود و بنابراین نقش اول آنها در مجموعه نام دادهشدهای بودن است. اینکه، این عناصر چه در خود دارند یا اصلاً وجود دارند یا نه، مسئله بعد است.
در ادامه این یادآور، فقط بر مبنای همینکه گفته شد، پس از بیان چند خاصیت مجموعهها، مفاهیم بس مهمی چون شمارش، شمارشپذیری، مقایسه، مقایسه پذیری، ترتیب, ترتیبپذیری، اصل عجیب انتخاب، بینهایتها و بسیار دیگر را مرور خواهیم کرد. امید آن است سپس بتوانیم ساختارهای ساختهشدهای در دانش کامپیوتر را ژرفتر واکاوی کنیم.
■ نظریه مجموعهها:
مجموعهها و درواقع نظریه مجموعهها (یا به گونه خاصتر نظریه مجموعههای بینهایت) یک دستگاه استنتاجی است. ریاضیدانان با چندین رهیافت این نظریه را بیان میکنند.ازجمله, نظریه طبیعی مجموعهها ➥, که در آن بهرهوری از زبان طبیعی حداکثری است و گرفتار ناسازگاری. اما بیان گوهری آن توسط دستگاههای اصل موضوعی ، ازجمله دستگاه موسوم به زیملو (تسرملو)-فرانکل با کوته واژه ZF و دستگاه موسوم به نویمان-برنیز-گودل با کوته واژه NBG، است.
دستگاه ZF به شمول اصل موضوع انتخاب با کوتهسازی ZFC و گاهی ZF+C ، بنیاد ریاضیات جاری (کلاسیک) است. دستگاه NBG و ZFC بسیار شبیه و نیز همساز هستند. تفاوت عمده در وجود انگارهی " کلاس"، که مجموعه گونهای از آن است، در دستگاه NBG است. [پایینتر، بند کلاس و مجموعه، توضیح کوتاه خواهد آمد.]
نظریه طبیعی مجموعهها (نه رهیافتهای اصل موضوعی) گرفتار ناسازگاری است. زیرا در نظریه طبیعی مجموعهها طبیعی است که «مجموعه همه مجموعهها» وجود داشته باشد. اما داشتن چنین مجموعهای، که آن را هنگام رسیدن به پارادوکس راسل خواهیم دید، ویرانگر است.
 داستانک
داستانک![]() :
:
در سرزمینی هر ساکن آن از یکی دو گونه T یا F است. افراد گونه T فقط گزارههای درست (راست) میگویند و افراد گونه F فقط گزارههای دروغ میگویند.
روزی یک از ساکنان گفت "آنچه میگویم برای اولین بار نیست که گفتهام."
پرسش . گوینده از چه گونهای است؟ از گونه T یا گونه F؟
برگرفته از: اسمولین۱
پاسخ. ➥.

■ زنجیرههای عضویتی کاهنده بیپایان
فرض کنید A∘ نام یک مجموعه باشد و نیز فرض کنید (فرض ممکن) A۱ عضو آن باشد. بنابراین مینویسیم A۱ ∈ A∘.
ازآنجاکه عضو یک مجموعه خود مجموعه است، A۱ میتواند دارای عضوی به فرض A۲ باشد و نوشت A۲ ∈ A۱. مجموعه A۲ نیز میتواند دارای عضوی بهفرض A۳ باشد و نوشت A۳ ∈ A۲. مجموعه A۳ نیز میتواند دارای عضو باشد و همینطور اعضای آن نیز. این زنجیره میتواند تا ابد ادامه یابد. به چنین زنجیرهای یک زنجیره عضویتی کاهنده بیپایان گفته. در زیر نمایشی از این زنجیره آمده:
A۱ ∈ A∘.
A۲ ∈ A۱ ∈ A∘.
A۳ ∈ A۲ ∈ A۱ ∈ A∘.
An+۱ ∈ An ∈ . . . ∈ A۳ ∈ A۲ ∈ A۱ ∈ A∘.
. . .
. . .
. . . ∈ An+۱ ∈ An ∈ . . . ∈ A۳ ∈ A۲ ∈ A۱ ∈ A∘.
با شدنی بودن چنین زنجیرهای عضویت دوری (عضویت مجموعه در خود) نیز شدنی بود. بهعبارتدیگر:
. . . ∈ B ∈ B ∈ B
شدنی بود. همینطور عضویت متقابل نیز شدنی بود. یعنی، زنجیره عضویتی بیپایان زیر شدنی بود:
. . . ∈ A ∈ B ∈ A ∈ B
در نظریه اصل موضوعی مجموعهها بهموجب یک قضیه زنجیرههای عضویتی کاهنده بیپایان نشدنی است. ازاینجهت گفته میشود سازواره مجموعهها خوش-بنیاد است.
■ کلاسها و مجموعهها:
در بیشتر متون، مگر آنکه قید شود، منظور از کلاس همان مجموعه است؛ با این اشاره ضمنی که اعضای آن خود میتوانند مجموعههای از پیش معین باشند. گاهی نیز بهجای کلاس وقتی منظور اینکه گفته شد باشد از عبارت خانواده-مجموعه استفاده میشود.
اما در دستگاه اصل موضوعی NBG کلاس یک انگاره آغازی (تعریفنشده) است. و مجموعه همچون گونهای از کلاس معرفی میگردد. این رهیافت با جان فون نویمان (م۱۹۲۵) آغاز و سپس توسط پال برنیز (م۱۹۳۷) ادامه و با کورت گودل (م۱۹۴۰) کامل گردید➥.
■ کلاس و مجموعه در NBG
ما اینجا نگاه فوری به دستگاه NBG میاندازیم. بیشتر را میتوان در دستگاه اصل موضوعی مجموعهها (NBG) دید.
در دستگاه NBG کلاسها که انگاره آغازیاند را به شرح زیر دستهبندی میکنند:
۱- کلاس سره: کلاسی است که در هیچ کلاسی نیست (عضو هیچ کلاسی نیست.)
۲- کلاس ناسره که به آن مجموعه [و همینطور عنصر] گفته کلاسی است که متعلق به کلاسی باشد.
بنابراین، همه عناصر [≈ همه مجموعهها] کلاس هستند ولی میتواند کلاسی عنصر [≈ مجموعه] نباشد. در دستگاه NBG بعضی کلاسها گستردهتر از آناند تا عنصر باشند. برای نمونه، کلاس همه عناصر که خود در خود نیستند (کلاس همه مجموعههایی که عضو خود نیستند) و نیز کلاس همه عناصر (کلاس همه مجموعهها) کلاس سرهاند.
■ نظریه کتگوریها:
آنگونه که نورمن استین رد / Norman Steenrod آن را نامید، زبان کتگوریها از روی لطف همچون "مهمل انتزاعی" شناختهشده. در اصل، این عبارت نه ضرورتاً موهن که دقیق هم است: کتگوریها به "مهمل" بدین برداشت رجوع دارند که آنها تماماً درباره "ساختار" هستند و نه درباره "معنی" آنچه نشان میدهند.
__ پائولو الفی / Paolo Aluffi.
مجموعهها را با چیزهای متعلق به چیزها آغاز کردیم. به همین ترتیب میتوان کتگوری (کاتگوری) (نظریه کتگوریها) را با ساختارها بر یا در) ساختارها آغاز کرد. نظریه کتگوری بررسی ساختارهاست که ازجمله یکسانیهای ارزشمند بین چیزهای (ساختارهای) بهظاهر بیربط را آشکار میکند. در این نظریه مجموعه خود یک کتگوری است.
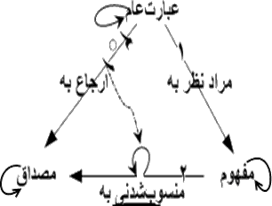
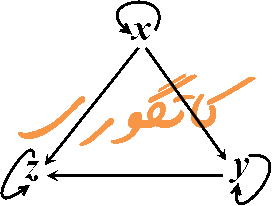
آغازگر این نظریه ساموئل النبرگ (Samuel Eilenberg, ۱۹۰۹-۲۰۰۵) و ساندرز مک لین (Saunders Mac Lane, ۱۹۱۳-۱۹۹۸)، که بهتمامی به شیوه اصل موضوعی گسترشیافته، هستند. در این نظریه، مجموعه خود گونهای کتگوری است (یعنی، همه مجموعهها کتگوری هستند.) نظریه کتگوریها دارای دو انگاره آغازی بهقرار چیز و پیکانه (نشانک) است که در آن پیکانهها از چیزها به چیزها نشانه رفتهاند.
در نمودار شماتیک زیر یک کتگوری شامل سه چیز و شش پیکانه نشان دادهشده.
 |  |
نظریه کتگوریها، بهجز در خود ریاضی، همچون زبان جهانی ریاضی، در دانش کامپیوتر، دانش شناختی و فلسفه کاربردهای مهم خود را دارد.
واژه کتگوری در نظریه کتگوری که اینجا بدان اشاره شد با مقولان ارسطویی (Aristotle's Categories)، گزارههای کتکوریک (حملی) و قیاسهای کتگوریک (حملی) بدون ارتباط است و بنابراین نباید به این واژگان ارسطویی ربط داده شود.
■ مراجع یادآور نظریه مجموعهها:
1- George Tourlakis, (2022). Computability, Springer International Publishing.
2- Eric Steinhart, (2018). More Precisely The Math You Need to Do Philosophy, Broadview Press.
3- Mendelson E., (2015). Introduction to Mathematical Logic, CRC Press.
در فصل ۴ (نظریه مجموعهها) این کتاب دقیقترین بیان دستگاه NBG را میتوان یافت.
4- Willem Conradie, Valentin Goranko (2015). Logic and Discrete Mathematics, John Wiley and Sons Ltd.
5- Raymond M. Smullyan, (2014). A Beginner’s Guide to Mathematical Logic, Dover Publications, Inc.
6- Charles C. Pinter (1971, 2014). A Book Of Set Theory, Dover Publications, Inc.
7- Daniel J. Velleman. (2006). How to prove it. A Structured Approach, Cambridge university press.
8- Devlin Keith J. (2003). Sets, Functions, and Logic An introduction to Abstract Mathematics, Chapman & Hall.
9- Ciesielski, K. (1997). Set Theory for the Working Mathematician (London Mathematical Society Student Texts, pp. I-Vi). Cambridge: Cambridge University Press.
برخی منابع برای نظریه کتگوریها:
۱- ریاضیات مفهومی (مناسب برای علاقهمندان با پیشزمینه ریاضی تا متوسط)؛ به آدرس:
http://fef.ogu.edu.tr/matbil/eilgaz/kategori.pdf
۲- درآمد به نظریه کتگوری (دانشگاه ویکی و مناسب برای علاقهمندان با پیشزمینه ریاضی متوسط)
https://en.wikiversity.org/wiki/Introduction_to_Category_Theory"
۳- مدخل در دانشنامه استنفورد (فلسفه)
https://en.wikiversity.org/wiki/Introduction_to_Category_Theory"
۵- نظریه کتگوری؛ به آدرس:
https://people.mpi-sws.org/~dreyer/courses/catlogic/awodey.pdf
۶- مبانی نظریه کتگوری برای دانش کامپیوتر؛