اصول موضوعه و دستگاه اصل موضوعی
یادآور نظریه اصل موضوعی مجموعه‌ها
درآمد به منطق و رایانش
۱- مقدمه: بنداشت و دستگاه بنداشتی | ۷- قضیه در دستگاه بنداشتی |
۲- انگارههای آغازین/ Primitive notions | ۸- استقلال بنداشت‌ها |
۳- بنداشت | ۹- سازگاری دستگاه بنداشتی |
۴- قواعد استنتاج | ۱۰- دستگاه حساب پئانو |
۵- دستگاه بنداشتی | ۱۱- مزایای روش بنداشتی و دستگاه‌های صوری |
۶- برهان در دستگاه بنداشتی |
دستگاه‌های بُنداشتی (اصل موضوعی) به نام‌های دستگاه صوری (Formal system) یا دستگاه حساب منطقی (Logical calculi) نیز شناخته می‌شوند.
■ مقدمه: بنداشت (اصل موضوع / Axiom) و دستگاه بنداشی
■ انگارههای آغازین / Primitive notions
انگاره آغازی [نیز عبارت تعریف‌نشده] آن مفاهیم در یک میدان سخن است که معنی آن، بدون تعریف، قابل‌فهم انگاشته شود. برای مثال در هندسه اقلیدسی انگاره‌هایی چون خط، دایره و مانند آنها تعریف‌نشده هستند.
• انگارههای تعریفی:
انگاره تعریفی (یا تعریف‌شده‌ها) آن مفاهیم در میدان سخن هستند که طبق قواعد مشخص (ساختار تعریف) از انگارههای تعریف‌نشده به‌دست‌آمده باشند.
■ بنداشت (اصل موضوع / Axiom)
بنداشت [یا گزاره آغازی / اصل موضوع] یک عبارت گزاره‌ای در میدان سخن است، به قسمی که حدود آن انگارههای آغازی یا انگارههای تعریفی در میدان سخن باشند و درستی آنها بدیهی انگاشته شود.
برای مثال گزاره ۱ تا ۵ در زیر اصول موضوعه هندسه اقلیدسی‌اند:
۱- از هر دونقطه می‌توان یک خط گذراند.
۲- هر پاره‌خط را می‌توان از دو سر نامحدود گستراند.
۳- یک دایره را می‌توان با مرکز و شعاع معلوم رسم کرد.
۴- همه گوشه‌های قائمه برابرند.
۵- اگر دو خط d و d' در صفحه با خط راست سومی قطع شوند، اگر اندازه جمع گوشه‌های داخلی در یک‌طرف خط سوم کمتر از دو قائمه باشد آنگاه دو خط d و d' در صورت ادامه، در همان طرفی که جمع گوشه‌های داخلی کمتر از دو قائمه است، یکدیگر را قطع میکنند. ➥
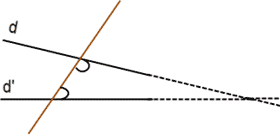
این صورت از اصل پنجم با صورت مشهور آن به‌قرار :
از هر نقطه خارج از یک خط حداکثر می‌توان یک خط موازی با آن رسم کرد.
هم‌ارز است. صورت اخیر به بُنداشت پلی فیر Playfair's axiom مشهور است.
■ قواعد استنتاج / Axiom
قواعد استنتاج در دستگاه بنداشتی قواعدی هستند که امکان استنتاج معتبر را از گزاره‌هایی که به‌عنوان مقدمه مفروض‌اند ممکن می‌سازند.
■ دستگاه بُنداشتی / Axiomatic System
یک دستگاه بُنداشتی شامل:
است.
برای مثال، در هندسه اقلیدسی بعد از بیان انگارههای آغازی، بنداشت‌ها و به‌طور ضمنی قواعد استنتاج، به گستراندن آنچه هندسه اقلیدسی نامیده پرداخته. یعنی: بر پایه انگارههای آغازی زنجیره‌وار مفاهیم جدید ساختن [تعریف کردن]؛ و نیز: کار زدن قواعد استنتاج منطقی، بر پایه بن انگاشته‌ها، و زنجیره‌وار قضیه جدید استنتاج کردن.
■ برهان (Proof) در دستگاه بنداشتی
یک برهان در دستگاه بنداشتی زنجیره‌ای متناهی از عبارت‌های گزاره‌ای است، به قسمی که هر عبارت این زنجیره یک بنداشت آن دستگاه باشد یا از عبارت‌های قبلی زنجیره و توسط کار زدن قواعد استنتاج آن دستگاه به دست آمده باشد.
■ قضیه (Theorem) در دستگاه بنداشتی
یک عبارت-گزاره‌ای یک قضیه در یک دستگاه بنداشتی است اگر و فقط اگر برهانی در آن دستگاه باشد که این عبارت-گزاره‌ای آخرین عنصر آن باشد.
: بنا بر تعریف قضیه، هر بنداشت یک قضیه است.
■ استقلال بنداشت‌ها / Independency of Axioms
بنداشت‌ها یک دستگاه بنداشتی را مستقل گویند اگر عضوی در هیچ زیرمجموعه‌ای از بنداشت‌های آن نباشد که بتواند، توسط قواعد استنتاج آن دستگاه، از بنداشت‌های آن دستگاه، که در این زیرمجموعه نیستند، به دست آید.
■ سازگاری دستگاه بنداشتی
یک دستگاه بنداشتی سازگار است اگر یک عبارت گزاره‌ای و نقیض آن هر دو در آن دستگاه قضیه نباشند.
■ دستگاه حساب پئانو
فارنام
xxxEnNm
جوزپه پئانو (۱۸۵۳ - ۱۹۲۰) Giuseppe Peano ریاضیدان ایتالیایی که بنداشت سازی اعداد طبیعی به‌افتخار وی به اصول پئانو مشهور است.
در کنار رهیافت بنداشتی هندسه اقلیدسی که در بالا دیدیم، کوتاه مفاهیم آغازی و بنداشت‌های حساب را نیز مرور می‌کنیم.
حساب به‌صورت بنداشتی برای اولین بار توسط ددکیند (۱۸۹۷) ریاضیدان آلمانی ارائه و کمی بعد با اندک تصرف به بنداشت‌های پئانو معروف گردید.
(آ): انگارههای آغازی:
۱- 
۲- عدد طبیعی ۳- تالی بی‌واسطه عدد طبیعی
[در بنداشت‌های زیر رابطه تساوی "=" با ویژگی‌های آن را پیش‌انگاشته گرفته.]
(ب): بنداشت‌ها:
| ۱- | عدد طبیعی است. |
| ۲- | تالی بی‌واسطه هر عدد طبیعی عدد طبیعی است. (برای عدد طبیعی n، تالی آن را با S(n) نشان داده.) |
| ۳- | تالی بی‌واسطه عدد طبیعی نیست. |
| ۴- | برای هر عدد طبیعی m و هر عدد طبیعی n، اگر تالی‌های بی‌واسطه m و n مساوی باشند آنگاه m=n. |
| ۵- | اصل استقرای ریاضی: گیریم Q یک ویژگی باشد. اگر آ: دارای ویژگی Q باشد، و ب: اگر عددی طبیعی دارای ویژگی Q باشد آنگاه تالی بی‌واسطه آن نیز دارای ویژگی Q باشد؛ آنگاه همه اعداد طبیعی دارای ویژگی Q هستند. |
| اکنون نماد ۱ را برای تالی گرفته، یعنی S() = ۱؛ نماد ۲ را برای تالی ۱ گرفته، یعنی S(۱) = ۲؛ و مانند آنها. | |
| تعریف جمع اعداد طبیعی (عملگر +) | = | 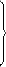 | آ: | a + = a |
| ب: | a + S(b) = S(a + b) |
برای مثال:
۱ + = ۱
(۱ + ۱) = (۱ + S()) = S(۱ + ) = S(۱) = ۲
۱ + ۲ = ۱ + S(۱) = S(۱ + ۱) = S(۲) =۳
| تعریف ضرب اعداد طبیعی (عملگر .) | = | 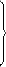| آ: | a . = |
| ب: | a . S(b) = a + (a . b) |
برای مثال:
a . ۱ = a . S() = a + (a . ) = a + = a.
(۳ . ۲) = (۳ . S(۱)) = (۳ + (۳ . ۱)) = ۳ + ۳ = ۶
از همین چند اصل و انجام اعمال شرح داده در بالا می‌توان به نظریه اعداد (قضیه اساسی حساب)، به ساخت اعداد گویا، اعداد حقیقی و بیشتر واصل شد [به‌صورت قضیه‌های اول ناتمامیت گودل و دوم ناتمامیت گودل نگاه کنید]. نظریه اعداد را به‌تمامی دقیق می‌توان در مندلسون و اسمولین یافت.
■ مزایای روش بنداشتی و دستگاه‌های صوری
از جمله کاربردهای دستگاه‌های صوری می‌توان فهرست زیر را ارائه کرد:
| ۱- | ایجاد استحکام و ژرفایی اندیشه ورزی به شیوه بنداشتی حتی با زبان طبیعی بطور بیشینه موجب حذف ابهام می‌گردد و تا حد امکان بر ذهنیت غلبه می‌کند و باعث عینیت بیشتر می‌گردد. |
| ۲- | تسهیل تفکر انتزاعی تفکر انتزاعی/ استدلال انتزاعی، شامل توانایی درک و تفکر در مورد مفاهیم پیچیده‌ای است که در عین واقعی بودن، به تجربیات، اشیاء، افراد یا موقعیت های عینی گره خورده نیستند. تفکر انتزاعی نوعی تفکر مرتبه بالاتر در نظر گرفته می‌شود که معمولاً درباره ایده‌ها و اصولی است که اغلب نمادین یا فرضی هستند. از طرف دیگر، تفکر انتزاعی روشی برای استدلال است - رویکردی سامان‌مند برای حل مسئله که شامل مفهوم‌سازی، کلی‌سازی و رسیدن به نتیجه‌گیری است. در تفکر انتزاعی، ما اطلاعات دریافتی از طریق حواس خود را پردازش می‌کنیم و سعی می‌کنیم آن را به جهان پیوند دهیم. بنابراین و از آنجا که دستگاه‌هاس صوری نمایانگر سیستم‌های خوش-تعریف هستند. آنها به ما اجازه می‌دهند تا در مورد مفاهیم پیچیده به روشی ساختاریافته و سیستماتیک استدلال کنیم. |
| ۳- | صحت سنجی الگوریتمیک برهان‌های صوری در ستگاه‌ها بنداشتی را می‌توان به صورت‌های الگوریتمیک پیاده سازی و توسط کامپیوتر بررسی کرد. این خود امکان صحت سنجی (Verification) مکانیکی براهین و استدلال‌ها را فراهم می‌کند. |
در نتیجه، دستگاه‌های بنداشتی / صوری نقش مهمی در بسیاری از زمینه‌ها ایفا میکنند. آنها چارچوبی محکم و دقیق برای استدلال ارائه می‌دهند، به عنوان پایه‌ای برای دانش عمل میکنند، تفکر انتزاعی را تسهیل میکنند، و صحت سنجی مکانیکی را میسر میکنند. همانطور که درک و استفاده از این سیستم‌ها همچنان در حال تکامل است، بدون شک آنها در شکل دادن به چشم انداز بسیاری از رشته‌ها ادامه خواهند داد.
