روند منطق مدرن، الگوریتم، محاسبه و تصمیم
منطق و فرامنطق
درآمد به منطق
روند منطق در چهار گام است. در این قسمت طرح این چهار گام [«زبان و فرازبان»، «تعبیر و مدل»، «دستگاه صوری» و «فرامنطق»] آمده است. سپس مراد نظر از مفهوم روند (process) واکاوی شده و مفاهیم بنیادینی چون «الگوریتم»، «محاسبه پذیری»، «تصمیمپذیری» و «مسئله توقف» در گستره منطق درخور این قسمت مورد بحث قرار گرفته شده است. (به روز رسانی: ۱۴۰۲/۰۱/۱۵)
 .۱ روند منطق مدرن، الگوریتم، محاسبه و تصمیم
.۱ روند منطق مدرن، الگوریتم، محاسبه و تصمیم
≡
۱- سرآغاز |
۶- رایانش پذیری (محاسبهپذیری - Computability) |
۲- شِمای منطق | ۷- تصمیمپذیری در تعلیق |
۳- روند | ۸- نیمی-تصمیمپذیر (semi-decidable) |
۴- ویژگیهای الگوریتم | ۹- خلاصه: الگوریتم، رایانشپذیری و تصمیمپذیری |
۵- مسئله توقف (Halting problem) | ۱۰- وجود تابع محاسبهناپذیر |
■ سرآغاز
هدف از این سلسله یادداشتها مرور منطق و مبانی نظری دانش کامپیوتر (Computer Sciencce) در گستره منطق و راستای حل مسئله است. این یادداشتها در واقع پینوشت بر کتاب «درآمد منطق؛ ایروینگ کپی، کارل کوهن، ویکتور رودیچ» است. مراجع مورد استفاده یادداشتها در متن یا در انتهای هر یادداشت آمده است.
موضوع چهار یادداشت بعدی پرتوافکنی بر تمایز بنیادین بین صورت و معنا، و رابطه آنها و مفهوم فرامنطق در منطق نوین است. این را مطابق با روندی (process) که آن را روند منطق مینامیم با نگاه نزدیکتر به فصلهای نهم (منطق نمادین) و دهم (روشهای استنتاج) کتاب «درآمد به منطق» به انجام خواهیم رساند. گرچه آنچه در این چهار یادداشت میآید در باره منطق گزارهای است اما چه منطق محمولات کلاسیک و چه منطقهای غیر کلاسیک مانند منطق شهودی (Intuitionistic Logic)، منطق مُدال (Modal Logic) و مانند آنها گام با چنین روندی دارند. این روند شامل چهار گام بهقرار زیر است که در ادامه شرح آن خواهد آمد.
۱- صورت: زبان صوری،
۲- معنا: مدل،
۳- برهان: دستگاه صوری،
۴- پیوند صورت و معنا: فرامنطق.
 ۱.۱ شِمای منطق
۱.۱ شِمای منطق
شِمای زیر فشردهای از آنچه
را در پیش رو داریم به نمایش میگذارد. | ||||||||||||||||||||
| زبان صوری (Formal Language) | ||||||||||||||||||||
| فرمول (فرمول خوش-ساخت) ( Well-Formed Formula / wff) | ||||||||||||||||||||
| دستگاه صوری Formal System
| نظریه مدل Model theory
| |||||||||||||||||||
فرازبان و فرامنطق (Metalanguage and Metalogic)
| |||||||||||||||||||
نمودار ۱. روند منطق (گزارهای کلاسیک) که در ادامه و در چهار یادداشت بعد شرح آن خواهد آمد.
پیش از گذر به یادداشت بعدی، باید تعاریف شهودی برخی از عبارات (الگوریتم - رایانشپذیری - تصمیمپذیری) را ارائه دهیم. در این یادداشت، هدف این است که تا حد امکان این عبارات روشن شوند. زیرا ما در این یادداشتها علاوه بر منطق آنگونه که در زبان متعارف شناخته میشود، در پی ارائه مبانی دانش کامپیوتر نظری، [نیز منطق محاسباتی] به عنوان گستره منطق نیز هستیم.
 ۱.۱ روند
۱.۱ روند

یک روند دنبالهای متناهی از اعمال مطابق قواعد معین برای دستیابی به یک نتیجه معین است، مانند روند دریافت یک مدرک تحصیلی، گرفتن گواهینامه رانندگی، ساختن خانه و مانند آنها. گرچه برای دستیابی به "نتیجه معین" باید روند آن اجرا گردد ولی اجرای روند الزاماً در زمان محدود به دستیابی "نتیجه معین" منجر نمیشود. افزون بر این، چندین روند برای دستیابی به "نتیجه معین" میتواند وجود داشته باشد.
 ۳.۱ الگوریتم
۳.۱ الگوریتم
مراد از یک الگوریتم [یا روند کارآمد / یا روند مکانیکی] روندی است که الزاماً در زمان محدود (گرچه به هر اندازه زیاد) به نتیجه منجر گردد. بهعبارتدیگر، الگوریتم دنبالهای متناهی از اعمال (دستورالعملها / قواعد) است به قسمی که اجرای آن در زمان محدود منجر به حل یک مسئله نوعی گردد. برای مثال، روندهای معمول در حساب برای جمع اعداد، ضرب اعداد، تقسیم دو عدد با تقریب دلخواه و جذر اعداد مثبت با تقریب دلخواه روندهای کارآمد هستند. وقتی یک الگوریتم برای محاسبه مقادیر یک تابع عددی، مانند ضرب، f(x,y)=x×y، استفاده میشود، تابع مورد نظر با عباراتی مانند، بطور الگوریتمیک قابل محاسبه، یا بطور کارآمد قابل محاسبه یا فقط محاسبه پذیر وصف میشود➥. ما در ادامه همین یادداشت در باره «محاسبه پذیری» بیشتر خواهیم گفت.
۴.۱ ویژگیهای الگوریتم
آنچه در باره الگوریتم در بند قبل آمد را میتوان با صراحت بیشتر در فهرست زیر بازگو کرد و آنها را ویژگیهای الگوریتم نامید➥.
فهرست متناهی دستورالعملها:
یک الگوریتم شامل دنبالهای متناهی از اعمال (دستورالعملها / قواعد)، به فرض:I۱, . . . . , Ik
است. هریک از این دستورها باید آشکاری و دقت کافی داشته باشد، آنگونه که اجرا کننده (ماشین) بتواند آن دستور را بدون ابهام اجرا کند. به ویژه، یک دستورالعمل نباید به هیچ ابتکار، نبوغ یا موجه سازی از جانب عاملی که دستور را اجرا می کند نیاز داشته باشد.
- گام به گام بودن اجرا در الگوریتم:
یک الگوریتم گام به گام طبق دستورالعملها پیش میرود. بنابراین در یک الگوریتم گام یک، گام دو، و مانند آن وجود دارد. - ورودی:
بیشتر الگوریتمها دارای گونهای ورودی، برای مثال، یک عدد، فهرست محدودی از اعداد، یک یا مجموعهای متناهی از صورتهای گزارهای (یا صورتهای صورتهای محمولی) و غیره خواهد بود. - پایان پذیری:
برای هر مجموعه از ورودیهای در دامنه مجاز، یک الگوریتم پس از تعداد محدودی از مراحل متوقف میشود و یک خروجی میدهد. این خروجی ممکن است پاسخ به یک سوال بله/خیر یا نتیجه محاسباتی باشد. (بعداً این الزام را کاهش میدهیم که یک الگوریتم باید برای هر ورودی متوقف شود.) - قطعیت (الگوریتم قطعی - Deterministic algorithm)
هر گام از یک الگوریتم بگونه یگانه تعیین میشود. بنابراین، اگر یک الگوریتم بیش از یک بار با ورودی(های) یکسان اجرا شود، خروجی یکسان خواهد بود. به عبارت دیگر، خروجی یک الگوریتم قطعی تنها و فقط تنها با ورودیهای آن معین میگردد.
☚: الگوریتم غیر-قطعی (Nondeterministic algorithm)
در علوم کامپیوتر نیز مفهوم الگوریتم غیر-قطعی وجود دارد. یک الگوریتم غیر قطعی الگوریتمی است که حتی برای ورودی یکسان، برخلاف الگوریتم قطعی، رفتارهای متفاوتی را در اجراهای مختلف از خود نشان میدهد. میتوان یک الگوریتم غیر قطعی را روی یک کامپیوتر رایج (قطعی) که تعداد نامحدود پردازنده موازی دارد پیاده سازی کرد⮫.
در واقع یک الگوریتم غیرقطعی یک مدل نظری است که در نقاط انتخاب (چند شاخه شدن)، فرض میشود که در صورت وجود شاخه موفق، «به طور جادویی» آن را انتخاب میکند (یا به طور معادل، همه شاخهها را به صورت همزمان بررسی میکند). ما در یادداشت ماشینهای تورینگ به این گونه الگوریتم برخواهیم گشت.
2- https://xlinux.nist.gov/dads/HTML/nondetermAlgo.html
☚: در مورد هر الگوریتم باید نشان داد (استدلال کرد):
۱- پایان پذیری الگوریتم (Termination of the algorithm): یعنی، اجرای آن برای هر ورودی(ها) در دامنه معین در زمان محدود به پایان میرسد.
۲- صحت الگوریتم (The correctness of the algorithm): خروجی الگوریتم صحیح است، یعنی همان و فقط همان چیزی است که در صورت مسئله تعریف شده است.
☚: الگوریتم، تفکر بازتابی و مکانیک
گرچه طراحی الگوریتم نیازمند به ابتکار (گاهی نبوغ) و موجه کردن آن است، اما پیاده سازی آن (برگردان آن به کد و اجرای آن توسط مجری) صرفاً یک عمل مکانیکی (ماشینی) است. از همین جهت است که گاهی به الگوریتم یک روند مکانیکی➥ میگویند.
☚: الگوریتم و کلاس الگوریتمها:
در فصل سوم و چهارم کتاب درآمد به منطق دیدیم که چگونه است که استدلال در زبان نمود مییابد. نمودگاه اول یک الگوریتم نیز زبان است. یعنی، یک الگوریتم به یک زبان نوشته میشود. این زبان میتواند فارسی یا یک زبان پیش ساخته باشد. بنابراین یک الگوریم مقدمتاً یک رشته متناهی به قاعده-ساخت از زبانی با الفبای متناهی است. پس میتوان از کلاس نامتناهی و شمارش پذیر الگوریتمها، یا فقط کلاس الگوریتمها نام برد.
• مثال: الگوریتم اقلیدس
در زیر، برای نمونه، روش مرسوم برای پیداکردن بزرگترین مقسوم علیه مشترک (ب.م.م) دو عدد طبیعی موسوم به روش نردبانی (نیز الگوریتم اقلیدس) آمده است. الگوریتم اقلیدس بر پایه این قضیه در حساب است که ب.م.م دو عدد a و bبرابر است با ب.م.م b و باقیمانده تقسیم a بر b.
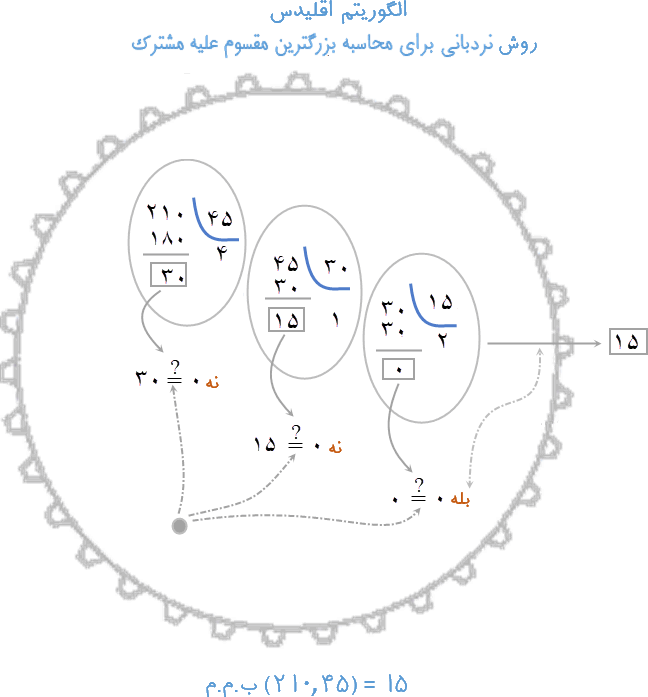
[میتوان نشان داد که اگر a بزرگتر یا مساوی از b باشد آنگاه باقیمانده تقسیم a بر b کوچکتر از نصف a است.]
| الگوریتم اقلیدس (محاسبه ب.م.م) | |
| I۱ | ورودی: اعداد طبیعی و مثبت x و y بقسمی که x ≥ y. |
| I۲ | باقیمانده تقسم x بر y حساب و مقدار آن r نامید شود. |
| I۳ | اگر r ≟ 0 آنگاه y را به عنوان ب.م.م به عنوان خروجی الگوریتم ارائه شود؛ وگرنه اجرا از دستور بعدی ادامه یابد. |
| I۴ | مقدار x را برابر y قرار داده (x ← y). |
| I۵ | مقدار y را برابر r قرار داده (y ← r). |
| I۶ | اجرا از دستور I۲ ادامه یابد. |
در مورد این الگوریتم باید نشان داد:
۱- پایان پذیری: یعنی، اجرای آن برای هر ورودی(ها) در دامنه مجاز در زمان محدود پایان مییابد.
۲- صحت: خروجی الگوریتم صحیح است، یعنی خروجی بزرگترین مقسوم علیه مشترک هر ورودی(ها) در دامنه مجاز آنها است.
اثبات هر دو مورد بالا را در حساب مقدماتی میتوان یافت [پایانپذیری بهطور شهودی قابل درک است.
• سه ویژگی بنیادین الگوریتم
پنج ویژگی الگوریتم که در بالا آمده است را میتوان در سه ویژگی بنیادین الگوریتم آنگونه که در زیر آمده است بازگویی کرد.
توالی (گام به گامی - Sequence):
توالی همان است که در گام به گام بودن الگوریتم در پنج ویژگی آن آمده است. به عبارت دیگر، توالی ترتیب (پیکربندی) دستورات در یک الگوریتم است. اهمیت توالی درتعیین نحوه کار و نتایج الگوریتم است. ترتیب دستورات باید دارای منطق و آشکار باشد تا بتوان الگوریتم را به درستی و کارآمد اجرا کرد.در حالت کلیتر، یادگیری به شیوه توالی (یادگیری دنبالهای) توانایی کسب، پردازش و یادآوری اطلاعات یا اقداماتی است، که به ترتیب خاصی پیکربندی میشوند. یادگیری به شیوه توالی برای مهارت های شناختی و حرکتی مختلف مانند زبان، موسیقی، تایپ کردن، رانندگی و ورزش ضروری است. یادگیری دنبالهای میتواند صریح یا ضمنی باشد، بسته به اینکه یادگیرنده از ساختار زیربنایی یا منظم بودن توالی آگاه باشد یا نباشد.
- چرخه تکرار (Iteration):
اگر به نمایانسازی اجرای اجرای الگوریتم اقلیدس برای محاسبه ب.م.م ۲۱۰ و ۴۵ بنگریم خواهیم دید یک محاسبه، یعنی یافتن باقیمانده تقسیم x بر y، سه دور (سه بار) تکرار شده است. این دورهای تکرار پیش رونده هستند، بدین معنی که، مورد محاسبه در هر دور، یعنی x و y با دور قبلی متفاوت هستند (در هر دور باقیمانده کوچکتر میشود). اگر نگوییم همه، قریب به اتفاق همه الگوریتمهای مفید حداقل در خود دارای یک چرخه تکرار هستند. بنابر این مراد از یک چرخه تکرار در الگوریتم (به عبارت دیگر در حل مسئله) دورهای متوالی و پیش رونده تکرار یک محاسبه نوعی است.
در الگوریتم دو گونه متفاوت چرخه تکرار میتواند وجود داشته باشد:
۱- چرخه تکرار، موسوم به چرخه کراندار نیز مشهور حلقه for، که تعداد دور تکرار در چرخه از پیش معین (ثابت) است. برای مثال، جمع متوالی اعداد طبیعی ۱ تا n.
۲- چرخه تکرار، موسوم به چرخه آزاد نیز مشهور به حلقه while، که تکرار دور بعدی درون خود چرخه با برآورد یک رابطه معین میشود. به رابطه مورد برآورد در چرخه آزاد، برای مثال رابطه r≟۰، یعنی صفر بودن باقیماند تقسیم در الگوریتم اقلیدس، رابطه معیار در چرخه تکرار نیز گفته میشود. - انتخاب (Selection):
دستورها در یک الگوریتم به طور پیش فرض یکی بعد از دیگری اجرا میشود. اما گاهی نیاز است بر اساس نتایج تاکنون به دست آمده، یعنی درستی یا نادرستی رابطهای، دستورالعمل بعدی انتخاب شود. برای مثال در الگوریتم اقلیدس در دستور I۳:
درستی یا نادرستی رابطه r = 0 تعیین کننده (انتخاب کننده) اجرای دستورالعمل بعدی است.I۳ اگر r = 0 آنگاه
y را به عنوان ب.م.م به عنوان خروجی الگوریتم ارائه شود؛
اجرای الگوریتم پایان یابد.وگرنه
اجرا از دستور بعدی ادامه یابد.
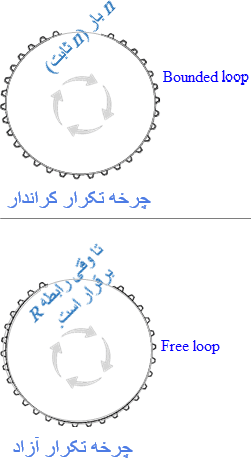
در یادداشتهای آینده خواهیم دید برای حل برخی مسائل، طراحی الگوریتم با صرفاً چرخههای کراندار میسر نیست.
اگر به حل مسئله نیز روش شناسی علمی و نیز به استقرای ریاضی و تعریفهای بازگشتی نگاه بیاندازیم سه گانه توالی، چرخه تکرار و انتخاب را میتوان در آنها یافت.
 ۵.۱ مسئله توقف (Halting problem)
۵.۱ مسئله توقف (Halting problem)

چه خواهد شد اگر در چرخه تکرار آزاد برای حل یک مسئله، رابطه معیار هیچ گاه برای خروج از چرخه برقرار نگردد؟ پاسخ تکرار ابدی سیزیف وار (Sisyphean task) است. این میتواند برگزیدن یک رابطه معیار بد یا محاسبه بد در درون چرخه باشد آنگونه که هیچ گاه رابطه معیار را بر نیاورد.
اکنون این پرسش که به مسئله توقف (Halting problem) مشهور است به میان میآید، که آیا الگوریتمی هست که در باره پایانپذیری روند (با ورودی دلخواه) پاسخ قطعی آری / نه دهد؟ پاسخ این است که نه تنها چنین الگوریتمی نیست بلکه طراحی چنین الگوریتمی خود-متناقض است. ما در قسمتهای بعدی به مسئله توقف برخواهیم گشت.
در کتاب «درآمد به منطق» فصل ۲ قسمت ۵ (مسئله و استدلال) گفته شده است که «اندیشیدن بازتابانه — خواه در جامعه شناسی، پزشکی، حقوق، فیزیک یا در هر قلمروی — کنشورزی حل مسئله است. بهعبارتدیگر، حل مسئله روندی است ذهنی که مستلزم تحلیل و آشکارسازی موضوعی از گونهای است. چرخه حل مسئله ....»![Bing AI. (2023). [Description of image]. Personal communication. چرخه بیکران – Uunbouded loop](img/TrappedInInfinty2.jpg)
مسئلههای برخاسته از جهان واقع و زندگی روزانه آن شست رفتگی (ساختارمندی - structuredness) پرسشهای آموزسی را ندارد و بیشتر آنها نه چندان ساختارمند هستند. اکنون اگر در چرخه حل مسئله به هر علت و دلیل گرفتار ورطه توقف ناپذیری شویم چه باید کرد؟ دیدیم که روش مکانیکی برای فهم دور باطل وجود ندارد. فعلاً آنچه میسر است ذهن باز و گیرایش رویدادها در بیرون از چهارچوبه مسئله است. این همان تفکر نقادانه است. یعنی آنچه عمدتاً در بخش اول و بخش سوم کتاب «درآمد به منطق» آمده است. اگر به دور باطل پی بردیم قدم اول درک بیشتر (چرایی) آن و سرانجام پرش به بازآرایی صورت مسئله و فهم دقیقتر زمینه (context) آن است.
 ۶.۱ رایانش پذیری (محاسبهپذیری - Computability)
۶.۱ رایانش پذیری (محاسبهپذیری - Computability)
در این بند در پی مفهوم مهم دیگری به نام محاسبهپذیری (Computability) و به عبارت بهتر رایانشپذیری هستیم که ارتباط تنگاتنگی با الگوریتم دارد. برای تعریف رایانشپذیری ابتدا باید بگوییم مراد ما از محاسبه چیست. رایانش (Computing) عبارت از همه اعمالی است که مجری الگوریتم (رایانه - حسابگر) برای اجرای الگوریتم و فقط اجرای الگوریتم انجام میدهد. اکنون میتوان گفت یک مسئله رایانشپذیر (محاسبهپذیر) است اگر الگوریتم حل آن مسئله وجود داشته باشد و یک مجری بتواند آن الگوریتم را محاسبه کند.
مجری چیست؟ (Model of Computation)
یک مجری یک مدل نظری است، یعنی یک ماشین انتزاعی، برای نمونه ماشینهای اندوختگانی (Register machines)، دستگاه توابع بازگشتی (Theory of recursion functions)، ماشینهای تورینگ (Turing machines)، دستگاه حساب لامبدا / λ-Calculus و مانند آنها.
به عبارت دیگر:
یک مدل رایانش [ماشین انتزاعی] (Model of Computation - Abstract machine) عبارت است از توصیف دقیق و صوری از نحوه محاسبه (رایانش) خروجی یک تابع با توجه به ورودی آن و نیز وصف نحوه سازماندهی واحدهای رایانش، حافظهها و رابطههای بین آنها⮫.
Abramsky, S. Introduction to processes and games (Handbook of the philosophy of information. Elsevier, Amsterdam 2008).
مدل رایانش چگونگی سازماندهی واحدهای محاسبات، حافظهها و ارتباطات را توصیف میکند. پیچیدگی محاسباتی یک الگوریتم را میتوان با توجه به مدلی از محاسبات اندازهگیری کرد. استفاده از یک مدل امکان بررسی عملکرد الگوریتمها را میسر میکند و این مستقل از تغییراتی که مختص پیادهسازیهای خاص و فناوری خاص هستند. ما در قیادداشتهای بعد به تفصیل به این مدلها به ویژه ماشینهای اندوختگانی، توابع بازگشتی و ماشینهای تورینگ میپردازیم.
 ۷.۱ تصمیمپذیری (Decidability)
۷.۱ تصمیمپذیری (Decidability)
یک مسئله نوعی که پاسخ آن آری / نه است را تصمیمپذیر گوییم اگر یک روند کارآمد وجود داشته باشد، به قسمی که به پاسخ آری یا نه (نه هر دو) منجر گردد. برای مثال، برای هر عدد دادهشده و هر دو عدد دلخواه یک روند کارآمد (یا الگوریتم) وجوددارد که با کارزدن آن میتوان تصمیم گرفت آیا عدد دادهشده حاصل جمع آن دو عدد دلخواه است یا نه.
میتوان به هر تابع n متغیری، به فرض تابع دو متغیری جمع f(x,y)=x+y، یک رابطه n+۱ گانه نظیر کرد. برای مثال به تابع جمع رابطه R(x,y,c) را نظیر کرد، به قسمی که:
R(x, y, c) ⇔ f(x,y) = c
بنابراین، ارتباط بین الگوریتم و تصمیمپذیری آشکاری مییابد.
 ۸.۱ تصمیمپذیری در تعلیق
۸.۱ تصمیمپذیری در تعلیق
• حدس (گمانه) کولاتز
"حدس کولاتز" (Collatz conjecture) به عنوان یک مسئله هنوز حل نشده در ریاضی به لوتار کولاتز (۱۹۹۰ - ۱۹۱۰) ریاضیدان آلمانی برمیگردد.
فرض کنید x یک عدد طبیعی مثبت دلخواه باشد. اگر x زوج است آنگاه x/۲ را حساب کنید؛ اگر x فرد است مقدار ۳x+۱ را حساب کنید. برای مقدار بدست آمده همین همین کار (محاسبه و تصمیمگیری) را انجام دهید و این تکرار را ادامه دهید. طبق گمانه کولاتز تکرار این محاسبه، آنگونه که گفته شد، برای هر عدد طبیعی مثبت به عدد ۱ میرسد، که ادامه آن به تکرار پایان ناپذیر دنباله:
→ ۱, ۴, ۲, ۱, ۴, ۲, ۱, ....
منجر میگردد.
گمانه کولاتز برای تا اعداد بسیار بزرگ که محاسبه آن از عهده کامپیوتر برمیآید درست است (برای کامپیوترها درست است!) و به گمانه بیشتر ریاضیدانان درست است. اما، هنوز اثبات ریاضی برای آن یافته نشده است و پاسخ به درستی گمانه کولاتز نه بله و نه نه است.
گمانه کولاتز در روند زیر بیان شده است.
| روند آزمون گمانه کولاتز (P.C.C.T) | |
| ☚: در روند زیر بجای عبارت ۳x+۱ عبارت (۳x+۱)/۲ بکار گرفته شده است، که این فقط بخاطر تولید اعضای دنباله کمتر و رسیدن زودتر به عدد ۱ در صورت ممکن بودن است. | |
| I۱ | ورودی: عداد طبیعی بقسمی که x > ۰. |
| I۲ | اگر x=۱ آنگاه "بله" به عنوان خروجی ارائه شود. اجرای روند پایان یابد. |
| I۳ | اگر x زوج است آنگاه x با x/۲ تعویض شود [x←x/2]. اجرا از دستور I۲ ادامه شود. |
| I۴ | اگر x فرد است آنگاه x با (۳x+۱)/۲ تعویض شود [x←(۳x+۱)/۲]. اجرا را از دستور I۲ ادامه داده. |
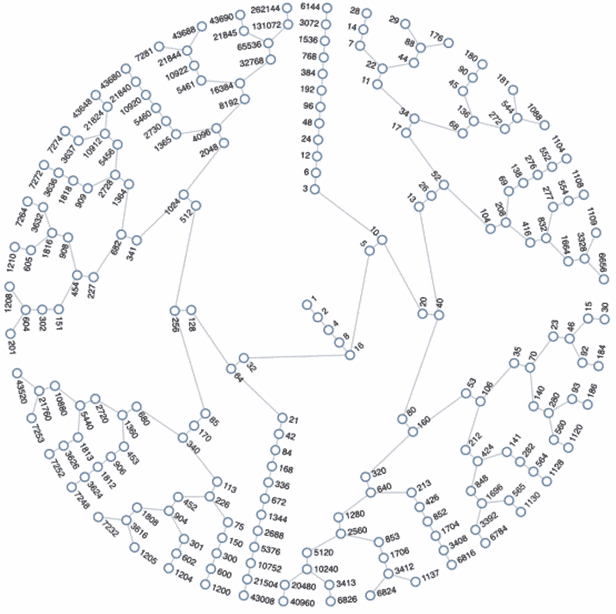
در شکل زیر گمانه کولاتز برای برخی اعداد نشان داده شده است.
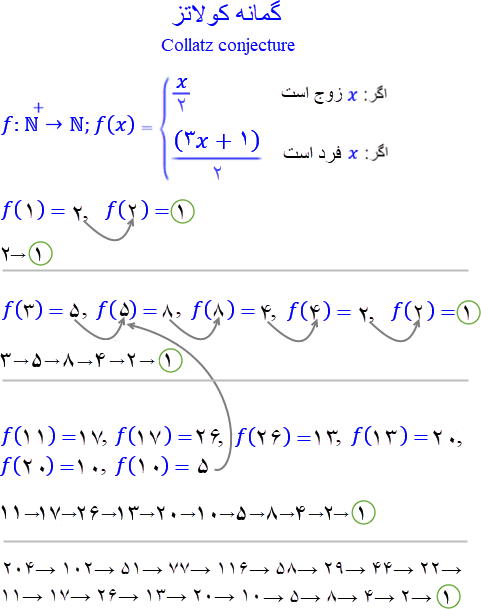
۲۷→ ۴۱→ ۶۲→ ۳۱→ ۴۷→ ۷۱→ ۱۰۷→ ۱۶۱→ ۲۴۲→ ۱۲۱→ ۱۸۲→ ۹۱→ ۱۳۷→ ۲۰۶→ ۱۰۳→ ۱۵۵→ ۲۳۳→ ۳۵۰→ ۱۷۵→ ۲۶۳→ ۳۹۵→ ۵۹۳→ ۸۹۰→ ۴۴۵→ ۶۶۸→ ۳۳۴→ ۱۶۷→ ۲۵۱→ ۳۷۷→ ۵۶۶→ ۲۸۳→ ۴۲۵→ ۶۳۸→ ۳۱۹→ ۴۷۹→ ۷۱۹→ ۱۰۷۹→ ۱۶۱۹→ ۲۴۲۹→ ۳۶۴۴→ ۱۸۲۲→ ۹۱۱→ ۱۳۶۷→ ۲۰۵۱→ ۳۰۷۷→ ۴۶۱۶→ ۲۳۰۸→ ۱۱۵۴→ ۵۷۷→ ۸۶۶→ ۴۳۳→ ۶۵۰→ ۳۲۵→ ۴۸۸→ ۲۴۴→ ۱۲۲→۶۱ → ۹۲→ ۴۶→ ۲۳→ ۳۵→ ۵۳→ ۸۰→ ۴۰→ ۲۰→ ۱۰→ ۵→ ۸→ ۴→ ۲→ ۱
فرض کنید x یک عدد طبیعی باشد که هنوز برای گمانه کولاتز آزمون نشده باشد. اگر x در گمانه کولاتز بگنجد آنگاه روند آزمون در بالا برای ورود x با پاسخ "بله" پایان مییابد. اما اگر ورودی، یعنی x، در گمانه کولاتز نگنجد آنگاه مجری این روند پس از چه مقدار زمان بازمیایستد؟ اگر ندانیم ورودی، یعنی x، در گمانه کولاتز میگنجد آنگاه مجری این روند در چه صورتی باز خواهد ایستاد؟
• n رقم متوالی ۷ در بسط عدد پی (π)
بیشتر ریاضیدانان تابع g(n) در زیر را یک تابع به حساب میآورند.

آیا این تابع تصمیمپذیر است؟ میدانیم یک روند مکانیکی برای تولید ارقام متوالی (یک به یک) در بسط اعشاری عدد پی (π) وجود دارد. بنابر این پایه، «روند» زیر را برای محاسبه g بکار میگیریم.
با توجه به n، شروع به تولید بسط اعشاری n، رقم به رقم نمایید و آن را چاپ نمایید. اگر در مرحلهای دقیقاً n عدد ۷ متوالی ظاهر شد، روند را متوقف کنید و مقدار ۱ را به عنوان مقدار تابع g(n) قرار دهید. اگر چنین دنبالهای از ۷ها ظاهر نشد، مقدار ۰ را به عنوان مقدار تابع g(n) قرار دهید.

مشکل این «روند» این است که، اگر برای یک n خاص، دنباله ای از n عدد ۷متوالی وجود نداشته باشد، هیچ گامی از روند وجود ندارد که بتوانیم توقف کنیم و نتیجه بگیریم که این همان مورد نظر ما است.
تا اینجا آنچه ما میدانیم، چنین دنبالهای از ۷ها ممکن است در بخشی از بسط عدد پی (π) ظاهر شود که هنوز بررسی نشده باشد. بنابراین این «روند» برای ورودی n برای g(n) = 0 برای همیشه ادامه مییابد. بنابراین این یک روند کارآمد نیست. (شاید تصور شود که روند کارآمدی برای محاسبه g بر اساس برخی از ویژگیهای نظری n وجود دارد. اما در حال حاضر چنین الگوریتمی شناخته شده نیست.➥)
• گمانه گلدباخ
از جمله گمانههای دیگر و معروف در ریاضی حدس گلدباخ (Goldbach Conjecture) است↜. مطابق این گمانه هر عدد زوج بزرگتر از ۲ مجموع دو عدد اول است (برای مثال: ۲۸=۲۳+۵ - ۴=۲+۲). این گمانه برای اعداد زوج بسیار بزرگ به آزمون در آمده است، که همگی آنها در جهت تایید آن بودهاند. اما خود حدس گلدباخ هنوز یک مسئله باز است، یعنی نه هنوز اثبات شده است و نه هنوز رد شده است↜.
 ۹.۱ نیمی-تصمیمپذیر (semi-decidable)
۹.۱ نیمی-تصمیمپذیر (semi-decidable)
همانطور که در گمانه کولاتز و تکرار رقم ۷ در بسط π دیدیم اجرای روندهای نظیر آنها وقتی پاسخ آری باشد پایان میپذیرند. در غیر این صورت، تا جایی که دانسته است، این روندها پایان نمیپذیرند. این یادآوری میتواند انگیزه برای تعریف «نیمی-تصمیمپذیر» باشد.
یک مسئله که پاسخ آن آری یا نه است را نیمی-تصمیمپذیر (Semi-Decidable) گوییم اگر روند حل آن فقط در صورت وجود پاسخ آری با خروجی "آری" پایان پذیرد؛ در غیر این این صورت، روند حل آن پایان ناپذیر (یا پاسخ "نه") باشد.
فرض کنید P یک مسئله نیمی-تصمیمپذیر باشد. شکل زیر وضعیت محاسبه پذیری P را نشان میدهد.
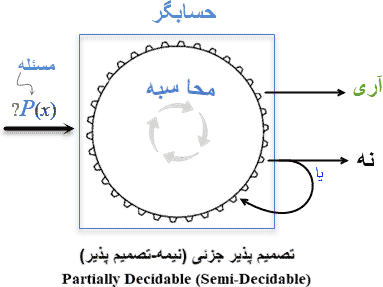
فرض بر اینکه P برای ورودی n، یعنی P(n)، تصمیمپذیر نیست ولی نیمی-تصمیمپذیر است. در این صورت، تا کی و کجا باید منتظر پاسخ باشیم؛ ۱ ثانیه، ۱ سال ۱۰۰۰۰۰۰۰۰۰ سال یا برای همیشه؟ این پرسش در خود نکتهای دارد و آن اینکه تشخیص تصمیمناپذیر بودن و به ویژه نیمی-تصمیمپذیر بودن یک مسئله چه اندازه زیادی اهمیت دارد و سرنوشت ساز است.
میتوان نشان داد، گرچه شهودی هم قابل درک است، که اگر مسئله P و ~P هردو نیمی-تصمیمپذیر باشند آنگاه P تصمیمپذیر است.
 ۱۰.۱ خلاصه: الگوریتم، رایانشپذیری و تصمیمپذیری
۱۰.۱ خلاصه: الگوریتم، رایانشپذیری و تصمیمپذیری
در اینجا آنچه در این یادداشت در باره الگویتم، تصمیمپذیری و رایانشپذیری گفته شد را خلاصه میکنیم.
فرض کنید A یک کلاس نامتناهی شمارا دلخواه و B، که میتواند نامتناهی نیز باشد، زیرکلاس دلخواه A باشد. [برای مثال، A کلاس اعداد طبیعی و B کلاس اعداد اول]. نیز فرض کنید x عضو دلخواه A است.

الگوریتم (روند کارآمد):
چه روند (پایان پذیر) طی شود تا عضویت x در B معین شود؟
رایانشپذیری:
به عبارت دیگر، آیا حسابگری وجود دارد تا الگوریتم عضویت x در B را محاسبه کند؟ به عبارت دیگر، آیا حسابگری وجود دارد تا عضویت x در B را محاسبه کند؟
تصمیمپذیری:
تصمیمپذیری ویژگی یک مجموعه (نیز رابطه) است. فرض کنید A یک کلاس باشد. آیا الگوریتمی وجود دارد که برای هر x دلخواه به پرسش عضویت x د A پاسخ قطعی آری / نه دهد؟ [به عبارت دیگر، آیا پرسش از رابطه x∈A دارای پاسخ قطعی آری / نه است.] اگر چنین باشد آنگاه به A یک تصمیم پذیر میگویند. در غیر این صورت به A، نیز رابطه x∈A، یک کلاس (یا رابطه) تصمیم ناپذیر میگویند.
در شکل زیر رابطه الگوریتم، تصمیمپذیری و رایانشپذیری نشان داده شده است.
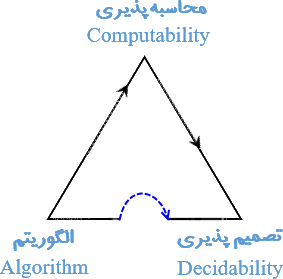
 ۹.۱ وجود تابع محاسبهناپذیر
۹.۱ وجود تابع محاسبهناپذیر
نشان میدهیم از مقدمات:
۱- همه توابع یک متغیری محاسبهپذیر هستند،
۲- تابع محاسبهپذیر وجود دارد.
تناقض حاصل میشود (برهان خلف).
برای اثبات A را کلاس همه توابع محاسبهپذیر یک متغیری میگیریم (میدانیم که A تهی نیست).
با توجه به اینکه کلاس الگوریتمها شمارا است و نظیر هر تابع محاسبهپذیر یک الگوریتم وجود دارد پس A شمارا است. بنابراین میتوان اعضای A را برشمرد: (در زیر دامنه تغییر x اعداد طبیعی است):
`f_{i in NN}: NN -> NN`; `<f_{i in NN}(x)> =`
`= f_۰(x), f_۱(x), . . . , f_n(x), . . .`
اکنون تابع یک متغیری `color(blue)(g)(x)` در زیر را در نظر بگیرید:
`color(blue)(g) :NN -> NN ; g(x) = f_x (x) + ۱`
بنا بر مقدمه، `color(blue)(g)` که یک تابع یک متغیری است باید عنصر دنباله `<f_{i in NN}(x)>` باشد. از این برمیآید که تابع `color(blue)(g)` باید همان `f_x (x)` باشد. پس:
`f_x (x) = f_x (x) + ۱`
این در دستگاه پئانو یعنی:
۰ = ۱
(برهان قطری کانتور و پارادوکس راسل را ببینید.)

