صورت، معنی و مدل - منطق گزارهها
منطق و فرامنطق
درآمد به منطق
دانستن معنای یک جمله، دانستن این است که اگر آن جمله درست میبود، جهان چگونه میبود.
__ Michael Dummett, Truth and Other Enigmas (1978)
 صورت، معنی و مدل در منطق گزارهها
صورت، معنی و مدل در منطق گزارهها
۱- مقدمه | ۱۷- از مدل (تعبیر) به فرمول |
۲- خیلی کوتاه درباره نظریههای معنا | ۱۸- مثال. (فرمول تعیین اکثریت) |
۳- تعبیر زبان `L^C` | ۱۹- تمامیت رابطهای تابع ارزشی |
۴- فرمول و مدل آن | ۲۰- قضیه: تمامیت گویاگر رابطها |
۵- مدل مجموعه فرمول | ۲۱- معرفی دو رابط جدید |
۶- مدل مجموعه تهی | ۲۲- قضیه: تمامیت گویاگرانه {↓} و {↑}. |
۷- صورت توتولوژیک | ۲۳- قضیه: ↓ و ↑ انجمنی نیستند. |
۸- صورت نامعتبر | ۲۴- قضیه: انحصار رابطهای دوتایی ↓ و ↑. |
۹- صورت متناقض | ۲۵- صورتهای نرمال (Normal Forms) |
۱۰- صدق پذیری و سازگاری معنایی | ۲۶- لیترال (Literal) |
۱۱- رابطه استلزام منطقی | ۲۷- صورت نرمال عطفی (Conjunctive Normal Form) |
۱۲- لم درخت | ۲۸- صورت نرمال فصلی (Disjunctive Normal Form) |
۱۳- رابطه همارزی منطقی | ۲۹- روند برگردان صورت گزارهای به صورت نرمال |
۱۴- آزمون اعتبار یک استنتاج سمانتیکی، بهوسیله مدل است. | ۳۰- یادداشت ۱: کارآمدی استنتاج سمانتیکی |
۱۵- چند نتیجه | ۳۱- یادداشت ۲: کامپیوترهای کوانتمی و پیچیدگی نمایی |
۱۶- صورت و معنی در منطق قدیم (ارسطویی) |
■ مقدمه
این قسمت کاوشی در صورت، معنا، تعبیر و مدل در منطق گزارهای است. با نظریه معنا و مفهوم مدل یک فرمول آغاز میکنیم. بهصورت سیستماتیک ساختار صوری سیستمهای منطقی را گسترش داده و از تعریف ویژگیهای بنیادی معنایی (Semantic) — مانند صدقپذیری (Satisfiability)، توتولوژی و استلزام منطقی — به بررسی کارایی رایانشی استنتاج معنایی خواهیم رسید. سپس توضیح میدهیم که چگونه پیچیدگی (Complexity)، که در چالشهای پیچیدگی نمایی و رایانش کوانتومی بروز مییابد، رویکردی را برای حل مسائل منطقی شکل میدهد. سرانجام، محدودیتهای ساختاری و توان گویایی سیستم ( LC) را با بررسی تمام بودن رابطهای تابع-ارزش، از جمله رابطهای غیراستاندارد مانند ↓ (نفی الزامی) و ↑ (نفی اختیاری)، بررسی میکنیم.
■ خیلی کوتاه درباره نظریههای معنا
در فصلهای ۱، ۲ و ۳ کتابدرآمد به منطق به تفصیل به زبان طبیعی پرداخته شده است و در همان ابتدا در ۱.۲ گفته شد جملات متفاوت میتوانند محتوای گزاره یکسانی باشند. نیز گفته شد که هر گزاره خود مدعی برقراری موردی بهطور واقع است یا مدعی برقراری موردی بهطور واقع نیست. بنابراین هر گزاره درست (راست /true) یا نادرست (دروغ /false) است. در منطق کلاسیک به مجموعه دو عضوی {درست، نادرست} — {True, False}، {راست، دروغ}، {صادق، کاذب} یا مانند آنها — مجموعه مقادیر ارزش (یا مقادیر معنایی) دوتایی و به هر عضو آن، یک مقدار معنایی / مقدار سمانتیکی (Semantic value) میگویند. در فصل ۴، تعریف چیست و کاربرد آن، نیز معنای عبارتهای عام بهتفصیل شرح داده شد.
برای مثال، جملههای "برف سفید است." و "Snow is white." را در نظر بگیرید. در این دو جمله "برف" و "Snow" هر دو به طور متعارف، هم در فارسی و هم انگلیسی، بخار متراکمی هستند که به شکل بلورهای یخ از ابر میریزند. و همینطور "سفید است" ("white")، بهطور متعارف به ویژگی (خاصیت) سفیدی [Whiteness] یا بهعبارتدیگر، به تابع گزارهای:
سفید_است(شیء)
یا
White(x)
ارجاع دارد، به قسمی که برای هر شیء = برف [یا x = Snow] داریم:
سفید_است(برف) = درست [یا، White(Snow) = True].
و البته چنین است که سفید_است(شیء) و White(x) دو تابع همارز سمانتیکی هستند چون تساوی تابعی وابسته به دامنه تعبیر (جهان سخن) است.
نظریههای معنا را میتوان به دو رده بهقرار: ۱- نظریههای سمانتیکی (Semantic theories)، ۲- نظریههای بنیادی معنا تقسیم کرد.
نظریههای سمانتیکی کوشش دارد تا به عبارات زبان، بهطور سازگار، مقدار سمانتیکی نظیر کند. نظریههای بنیادی معنا کوشش دارد توضیح دهد چه روندی موجب شده تا عبارات زبان (طبیعی) دارای آن مقادیر سمانتیکی باشند. به عبارت دیگر «یک نظریه بنیادی معنا میکوشد توضیح دهد چه چیز در مورد افراد یا گروهها به نمادهای زبان آنها معنا میدهد↓». توضیح بیشتر را میتوان در فصل ۳ (زبان و کارکردهای آن)، فصل ۴(تعریف) کتابدرآمد به منطق و نیز اینجا↓ دید. برای مثال:
فرض کنید کسی بگوید: «هوا سرد است.» در نظریه قصدی معنا↥، این جمله فقط گزارشی درباره دما نیست. بسته به زمینه، گوینده ممکن است قصد داشته باشد که: «شنونده پنجره را ببند»، «بخاری را روشن کند»، یا «لباس گرمتری بپوشد». بنابراین، آنچه به جمله معنا میدهد، صرفاً صدق یا کذب آن نیست، بلکه شبکهای از قصدهای بازشناختپذیر (Anagnorisis) است.
از دیدگاه نظریه قصدی معنا: معنای عبارات زبانی تابعی از قصد ارتباطی گوینده است، و زبان را میتوان مجموعهای از قراردادهای اجتماعی تثبیتشده دانست که انتقال این قصدها را در کنشهای ارتباطی ممکن میسازند.➥
1- Grice, H. P. Utterer’s meaning and intentions. The Philosophical Review, 1969, 78(2), 147–177.
2- Schiffer, S. Meaning. Oxford University Press, 1972.
3- Grandy, Richard E. and Richard Warner, "Paul Grice", The Stanford Encyclopedia of Philosophy (Fall 2023 Edition), Edward N. Zalta & Uri Nodelman (eds.), URL = <https://plato.stanford.edu/archives/fall2023/entries/grice/>.
1- Speaks, Jeff, "Theories of Meaning", The Stanford Encyclopedia of Philosophy (Spring 2021 Edition), Edward N. Zalta (ed.), URL = https://plato.stanford.edu/archives/spr2021/entries/meaning/.
■ تعبیر زبان LC:
در فصل ۹ کتابدرآمد به منطق و در قسمتهای ۲ (نمادگذاری ترکیب عطفی، نقیض و ترکیب فصلی) و ۳ (گزاره شرطی) با بهره جستن از زبان طبیعی، یعنی آنچه عمدتاً در فصلهای ۱ تا ۴ کتابدرآمد به منطق آمده است، مجموعه دو عضوی {درست، نادرست} همچون مجموعه مقادیر ارزش [همچنین: مقادیر معنایی یا مقادیر سمانتیکی] تعریف و تثبیت گردید. سپس کوشش شد تا صورتهای گزارهای برحسب این مقادیر تعبیر گردند.
مراد از تعبیر در زبان صوری LC یک روند کارآمد است تا بتوان با آن فرمولهای LC را به مقادیر معنایی برآوُرد. در این روند ابتدا به متغیرهای گزارهای مقادیر سمانتیکی گمارده، سپس طبق قواعد معینِ تثبیتشده و برحسب مقادیر معنایی گمارده به متغیرهای گزارهای، مقدار معنایی فرمولها معین میگردد. تعریف ساختار جداول ارزش رابطها که در کتابدرآمد به منطق آمده است، همان قواعد معین تثبیت شده هستند.
برای مثال اگر متغیرهای گزارهای LC فقط q، p و r باشند آنگاه:
تعبیر I۱ میتواند گمارش: درست←p، نادرست←q و درست←r؛
تعبیر I۲ میتواند گمارش: نادرست←p، درست←q و نادرست←r باشد.
در تعبیر I۱ مقدار معنایی صورت گزارهای (p∨q)⊃p بنا به تابع تعبیر (جدول ارزش) «درست» برآورد میگردد. این برآورد را اینگونه:
درست → ((p∨q)⊃p)I۱
نشان میدهند. و به همین ترتیب نیز مینویسند:
. نادرست → ((p∨q)⊃p)I۲
ازآنجاکه در هر تعبیر، کارکرد واژگان '≡' ,'~' ,'⊃' ,' '•,'∨' تعریف و تثبیتشده است، به آنها رابطهای منطقی [همچنین ثابتهای منطقی، رابط جمله گانی و واژگان منطقی ] در LC گفته میشود. و ازآنجاکه در هر تعبیر، به متغیرهای گزارهای مقادیر سمانتیکی گمارده میشود، به آنها واژگان نامنطقی در LC میگویند.
در ادامه (در کتابدرآمد به منطق)، با توجه و بر مبنای تعبیر، آنگونه که شرح آن آمد، مفاهیمی چون صورت گزارهای توتولوژی، تناقض، همارزی منطقی و استلزام منطقی معرفی گردید. اکنون چند تعریف را مرور میکنیم.
■ فرمول و مدل آن:
گیریم j یک تعبیر و α فرمول باشد. گوییم j برای α مدل است (یا α در j مدل است) اگر و فقط اگر درست=(α)j. برای مثال، تعبیر I۱ در بالا برای فرمول (p∨q)⊃p مدل است. حالآنکه تعبیر I۲ در بالا برای همین فرمول مدل نیست.
• نتیجه:
گیریم j یک تعبیر و α فرمول باشد. j برای α مدل است اگر و فقط اگر j برای ~α مدل نباشد.
■ مدل مجموعه فرمول:
گیریم j یک تعبیر و S مجموعه فرمول:
{α۱, α۲, . . ., αn}
باشد. گوییم j برای S مدل است اگر و فقط اگر برای:
α۱•α۲• . . .•αn
مدل باشد. بهعبارتدیگر، j بهطور همزمان مدل فرمولهای α۱, α۲, . . ., αn باشد. به بیان دیگر، اگر و فقط اگر تعبیری نباشد که برای فرمولی در S مدل نباشد.
■ صورت توتولوژیک:
یک فرمول را توتولوژی (یا صورت توتولوژیک) گوییم اگر و فقط اگر هر تعبیر آن، مدل آن نیز باشد. صورت توتولوژیک را، صورت معتبر (یا فقط معتبر) نیز مینامند.
■ صورت نامعتبر:
یک فرمول را نامعتبر (یا صورت نامعتبر) گوییم اگر و فقط اگر توتولوژی نباشد.
■ صورت متناقض:
یک فرمول را تناقض (یا صورت متناقض) گوییم اگر و فقط اگر مدل نداشته باشد.
■ صدق پذیری و سازگاری معنایی:
یک فرمول (و نیز مجموعهای از فرمول) را صدق پذیر گوییم اگر و فقط اگر حداقل یک مدل داشته باشد. به یک فرمول یا مجموعه فرمول صدق پذیر، منطقاً سازگار و همچنین بهطور معنایی سازگار نیز گفته میشود.
همچنین، یک فرمول (و نیز مجموعهای از فرمول) را صدق ناپذیر گوییم اگر و فقط اگر دارای مدل نباشد. به یک فرمول یا مجموعه فرمول صدق ناپذیر، منطقاً ناسازگار و همچنین بهطور معنایی ناسازگار نیز گفته میشود.
■ رابطه استلزام منطقی:
گیریم β فرمول و S={α۱, α۲, . . ., αn} که در آن n عدد طبیعی دلخواه است، یک مجموعه فرمول باشد. گوییم بین S و β رابطه استلزام منطقی برقرار است اگر و فقط اگر هر مدل S مدل β نیز باشد - بهعبارتدیگر، چنین نیست که تعبیر j باشد به قسمی که،
درست(α۱•α۲• . . .•αn)j= و نارست(β)j=.
رابطه استلزام منطقی را با نماد ⊩ نمایش داده و وقتی رابطه استلزام منطقی بین S و β برقرار باشد مینوسیم:
(آ):S ⊩ β
به بیان دیگر و معادل میتوان گفت:
S ⊩ β اگر و فقط اگر چنین نباشد که تعبیر j باشد به قسمی که:
درست(α۱•α۲• . . .•αn)j= و نارست(β)j=.
اگر S⊩β، آنگاه نیز گفته میشود، S منطقاً مستلزم β است و نیز، β نتیجه منطقی S است.
میتوان در S ⊩β بهجای S اعضای آن را فهرست کرد و نوشت:
(ب): α۱, α۲, . . ., αn ⊩ β
به (ب) در بالا وقتی برقرار است یک استنتاج معتبر سمانتیکی یا استنتاج سمانتیکی نیز گفته میشود.
اگر S تهی باشد، معمولاً بهجای ∅ ⊩ β فقط مینویسند:
⊩β :('آ).
اگر رابطه ('آ) برقرار باشد آنگاه β توتولوژی خواهد بود، زیرا با توجه به ↝ و تعریف استلزام منطقی، تعبیری نیست که مدل β نباشد.
پس میتوان نوشت:
β توتولوژی است اگر و فقط اگر ⊩ β.
تعریف:
گیریم S مجموعه فرمول؛ بنابر تعریف مینویسیم S ⊩ اگر و فقط اگر S مدل نداشته باشد.
■ لم درخت:
گیریم α فرمول و S مجموعه فرمول، آنگاه داریم:
S ⊩ α ⇔ S, ~α ⊩
اثبات:
اگر S ⊩ α آنگاه تعبیری نیست که مدل S باشد و مدل α نباشد. بنابراین تعبیری نیست که مدل S باشد و در عین حال مدل ~α هم باشد. پس بنا به (ب).۹. ۰ داریم: S, ~α ⊩.
اگرS, ~α ⊩ آنگاه، بنابر (ب).۹. ۰، تعبیری نیست که مدل S و ~α باشد. اما، بنابر (ب).۱.۳. هر تعبیر که مدل S باشد مدل ~α نخواهد بود. باشد. پس بنابر (ب).۹. ۰ داریم: S, ~α ⊩.
■ رابطه همارزی منطقی:
گوییم فرمولهای α و β همارز منطقی هستند اگر و فقط اگر هر مدل α مدل β نیز باشد. در این صورت مینویسیم:
α  β.
β.
(بهآسانی میتوان نشان داد  یک رابطه همارزی است.)
یک رابطه همارزی است.)
■ آزمون اعتبار یک استنتاج سمانتیکی، بهوسیله مدل است.
مثال ۱: نشان دهید: (p⊃q) ⊩ (~q⊃~p)
جدول ارزش زیر نشان میدهد هر تعبیر که برای p⊃q مدل است برای ~q⊃~p نیز مدل است. بنابراین ~q⊃~p نتیجه منطقی p⊃q است. بهعبارتدیگر:
(p ⊃ q) ⊩ (~q ⊃ ~p)
یک استلزام منطقی معتبر است.
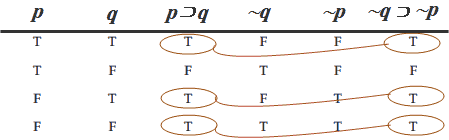
مثال ۲: نشان دهید:
p⊃(q⊃r), q⊃(p⊃r) ⊩ (p∨q)⊃r
یک استنتاج سمانتیکی معتبر نیست.
جدول ارزش زیر نشان میدهد: حداقل یک تعبیر (I4 ی I6) برای مقدمات مدل است ولی برای نتیجه مدل نیست
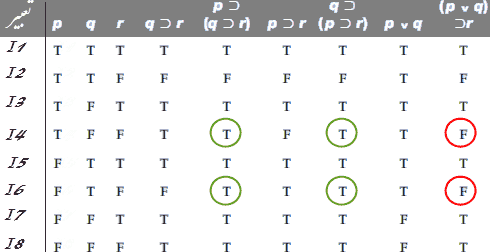
{p⊃(q⊃r), p⊃(q⊃r)} ⊩ (p∨q)⊃r
مثال ۳: نشان دهید:
I: ((p•q)⊃r)) ⊩ ((p⊃r)∨(q⊃r))
یک استلزام منطقی است.
۱- فرض خلاف: I یک استلزام منطقی نیست. به عبارت دیگر، تعبیر j یافت میشود، به قسمی که؛
j مدل (p⊃r)∨(q⊃r) نباشد و درعینحال مدل (p•q)⊃r باشد.
۲- اگر j مدل (p⊃r)∨(q⊃r) نباشد، آنگاه j نه مدل (p⊃r) و نه مدل (q⊃r) خواهد بود.
۳- اگر j مدل p⊃r نباشد آنگاه j مدل p است ولی مدل r نیست.
۴- گر j مدل q⊃r نباشد آنگاه j مدل q است ولی مدل r نیست.
۵- از۱، ۳ و ۴ داریم j مدل r و نیز مدل p•q است.
۶- از ۵ داریم j مدل (p•q)⊃r است، که خلاف فرض است.
نیز میتوان نشان داد هر مدل (p⊃r)∨(q⊃r) مدل (p•q)⊃r نیز هست. بنابراین میتوان نوشت:
((p•q)⊃r)) 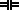 ((p⊃r)∨(q⊃r)).
((p⊃r)∨(q⊃r)).
■ چند نتیجه:
۱- α توتولوژی است اگر و فقط اگر ~α یک تناقض باشد.
۲- اگر α توتولوژی باشد آنگاه صدق پذیر است، ولی عکس آن میتواند درست نباشد (برای مثال، فرمول p صدق پذیر است اما توتولوژی نیست.)
۳- α نامعتبر است اگر و فقط اگر حداقل تحت یک تعبیر نادرست باشد.
۴- اگر α تناقض باشد آنگاه نامعتبر است، ولی عکس آن میتواند درست نباشد(برای مثال، p⊃~p نامعتبر اما صدق پذیر است.)
۵- رابطه (ب) برقرار است اگر و فقط اگر (α۱• α۲• . . .• αn )⊃β توتولوژی باشد. ازاینجهت در منطق گزارهای به رابطه استلزام منطقی رابطه استلزام توتولوژیک نیز گفته میشود.
۶- فرض کنید α≡β فرمول باشد. اگر این فرمول در (برای) تعبیری مدل باشد، فرمول α≡β در این تعبیر همارزی مادی است. برای مثال p•~q≡p∨~q در تعبیر j [نادرست(q)j=، درست(p)j=] همارزی مادی است. اما همین فرمول برای تعبیر i [درست(q)i=، درست(p)i=] همارزی مادی نیست.
۷- فرض کنید α≡β فرمول، گوییم این فرمول یک همارزی منطقی است اگر و فقط اگر در هر تعبیر مدل باشد، بهعبارتدیگر توتولوژی باشد. <<مناسب است قسمتهای ۸ و ۹ فصل ۱۰ کتابدرآمد به منطق مرور شود. >>
۸- اگر α و α⊃β توتولوژی باشند آنگاه β نیز توتولوژی خواهد بود. زیرا:
از آنجا که α و α⊃β توتولوژی هستند پس هر تعبیری برای آنها مدل است. اگر تعبیری برای β مدل نباشد آنگاه α⊃β توتولوژی نخواهد بود (چون طبق فرض α توتولوژی است) و این خلاف فرض توتوتولوژی بودن α⊃β است.
۹- α ⊩β اگر و فقط اگر ⊩α⊃β. گیریم ⊩α⊃β پس α⊃β توتولوژی است. ازاینجا، تعبیری نیست که مدل α باشد و مدل β نباشد. بنابراین داریم ⊩α⊃β ⇒ α⊩β و وارون آن نیز. به همین ترتیب میتوان نوشت:
α, γ ⊩β اگر و فقط اگر ⊩α⊃(γ⊃β).
بند د: استدلال، گزارههای شرطی و توتولوژی را ببینید.
۱۰- قضیه:👁↝ (جانشین سازی) ☚↧ گیریم 𝒯 یک توتولوژی شامل حروف گزارهای:
Mendelson, Elliott. Introduction to mathematical logic. 6th,ed, CRC Press, Taylor & Francis Group. 2015. (1.3)
p۱, p۲, . . ., pn,
باشد. نیز، ℬ از جایگزینی صورتهای گزارهای:
ℬ۱, ℬ۲, . . ., ℬn,
در 𝒯 به ترتیب برای p۱, p۲, . . ., pn به دست آمده باشد. در این صورت، ℬ نیز توتولوژی است. به عبارت دیگر، جانشینی در یک توتولوژی یک توتولوژی را به دست میدهد.
مثال:
𝒯 را (p۱ ∧ p۲) ⊃ p۱ بگیرید. نیز، ℬ۱ و ℬ۲ را به ترتیب (P∨Q) و (Q∧S) بگیرید. در این صورت، ℬ به قرار زیر:
(ℬ۱ ∧ ℬ۲) ⊃ ℬ۱
⇓
((P ∨ Q) ∧ (Q ∧ S)) ⊃ (P ∨ Q)
توتولوژی است.
اثبات:
فرض کنید 𝒯 یک توتولوژی باشد. برای هر گمارش مقادیر ارزش به حروف گزارهای در ℬ برای صورتهای:
ℬ۱, ℬ۲, . . ., ℬn,
ین صورتها به ترتیب دارای مقادیر ارزش:
v۱, v۲, . . ., vn,
هستند (که در آن هر xi 'د' یا 'ن' است). اگر این مقادیر v۱, v۲, . . ., vn را به ترتیب به:
p۱, p۲, . . ., pn,
بگماریم، آنگاه مقدار ارزش حاصل شده برای 𝒯 عبارت است از مقدار ارزش ℬ برای این مقایر ارزش. اما، 𝒯 یک توتولوژی است و برای هر گمارش به حروف گزارهای آن درست است. بنابراین، ℬ همیشه مقدار درست را میگیرد.
۱۱- قضیه:👁↝☚↧
Mendelson, Elliott. Introduction to mathematical logic. 6th,ed, CRC Press, Taylor & Francis Group. 2015. (1.4)
فرض کنید C۱ از B۱ با جایگزینی ς به جای یک یا چند مورد از رویداد 𝔓 در B۱ به دست آمده باشد. در این صورت،
(𝔓 ≡ ς) ⊃ (B۱ ≡ C۱)
یک توتولوژی خواهد بود. (بنابراین اگر 𝔓 و ς منطقاً همارز باشند آنگاه B۱ و C۱ نیز چنین خواهند بود.)
مثال:
B۱ را (C∨D)بگیرید. 𝔓 را ς بگیرید. ς را (~(~ς)) بگیرید. در این صورت،
C۱ ← (~(~ς)) ∨ D).
چون ς و (~(~ς)) همارز منطقی هستند، (ς∨D) و (~(~ς))∨D نیز همارز منطقی خواهند بود.
اثبات:
اگر 𝔓 و ς در هر گمارش مقادیر ارزش به حروف گزارهای دارای مقادیر ارزش مخالف باشند، آنگاه (𝔓≡ς) مقدار نادرست خواهد داشت و بنابراین،
(𝔓 ≡ ς) ⊃ (B۱ ≡ C۱)
دارای مقدار درست خواهد شد.
اگر 𝔓 و ς در هر گمارش مقادیر ارزش به حروف گزارهای دارای مقادیر ارزش یکسان باشند، آنگاه مقدار ارزش B۱ و C۱ در گمارش نیز چنین است. چرا که، تفاوت C۱ از B۱ فقط در این است که در جاهایی که 𝔓 در B۱ رخ داده است ς جایگزین شده است. بنابراین، در این حالت نیز (𝔓≡ς) دارای ارزش درست و (B۱ ⇔ C۱) نیز دارای مقدار ارزش درست است. و از اینجا،
(𝔓 ≡ ς) ⊃ (B۱ ≡ C۱)
■ صورت و معنی در منطق قدیم (ارسطویی)
در نزد ارسطو و منطق (قدیم) صورت/Form و صوری/Formal متفاوت از صورت، صوری و معنی در منطق جدید است. در منطق ارسطویی هیچ تفکیک روشنی بین صورت و معنا وجود ندارد. نزد ارسطو صورت و صوری واژهای متافیزیکی و نه منطقی و بحث آن نیز در مبحث متافیزیک (ماده و صورت) است↧.
Ainsworth, Thomas, "Form vs. Matter", The Stanford Encyclopedia of Philosophy (Summer 2020 Edition), Edward N. Zalta (ed.), URL = https://plato.stanford.edu/archives/sum2020/entries/form-matter/.
معنا یا سمانتیک در منطق ارسطو به محتوای واقعی یا موضوع استدلال اشاره دارد. این شامل مفاهیم، ایدهها و گزارههایی است که در مورد آنها استدلال میشود. ارسطو بر این باور است که آنچه میتوانیم «صحت متافیزیکی» بنامیم، شکل علمی دقیقتری از بیان منطقی ایجاد میکند. او دیدگاهی همه جانبه و از جمله متافیزیکی به منطق دارد و در عین حال معتقد است که این «صحت متافیزیکی» (Metaphysical correctness) به گزارههای درست منجر می شود.↧
Louis F. Groarke. Internet encyclopedia of internet. URL = https://iep.utm.edu/aristotle-logic#H3"
■ از مدل (تعبیر) به فرمول
در این یادداشت (نیز در فصل نهم کتاب درآمد به منطق) دیدیم که چگونه میتوان توسط جدول ارزش، تعبیرهایی را که مدلهای یک فرمول (صورت گزارهای) هستند یافت. در اینجا میخواهیم وارون این روند را شرح دهیم، یعنی روند یافتن صورت (فرمول) یک جدول-ارزش داده شده را. مثال زیر صورت مسئله را بیشر روشن میکند.
مثال:
میخواهیم فرمول x را بیابیم آن گونهای که فقط از دو اتم تشکیل شده و بعلاوه فقط دارای دو مدل به ازای گمارش مقادیر ارزش 'ن' برای هر دو اتم یا 'د' برای هر دو اتم آن، باشد.
حل:
چون x فقط دو اتم، به فرض p و q، دارد خلاصه جدول ارزش آن باید به گونه زیر باشد (یعنی فقط تعبیرهای I۱ و I۴ برای x مدل باشند):
| s تابع گمارش | ۱ | ۲ | ۳ |
| تعبیر(ها) | p | q | (x)I |
| I۱ | s(p) = د | s(q) = د | د |
| I۲ | s(p) = د | s(q) = ن | ن |
| I۳ | s(p) = ن | s(q) = د | ن |
| I۴ | s(p) = ن | s(q) = ن | د |
جدول بالا را میتوان به فارسی این گونه بازگو کرد:
x را بیاید به قسمی که x فرمول LC و فقط تحت آن تعابیر مدل باشد که:
s(p) = د و s(p) = د
یا
(p) = ن و s(p) = ن
برای پیدا کردن x یک ستون به جدول اضافه میکنیم (ستون ۴). در این ستون و در آن سطرها که مدل هستند صورت عطفی محض متشکل از دو اتم را به قسمی مینویسیم که اگر مقدار ارزش هر یک از اتمها در آن سطر درست است خود آن اتم وگرنه نقیض آن اتم حضور یافته باشد. در این مثال اگر چنین کنیم جدول زیر به دست میآید (ε در این سطر هیچچیز است):
| s تابع گمارش | ۱ | ۲ | ۳ | ۴ |
| تعبیر(ها) | p | q | (x)I | صوتهای عطفی |
| I۱ | د | د | د | p • q |
| I۲ | د | ن | ن | ε |
| I۳ | ن | د | ن | ε |
| I۴ | ن | ن | د | ~p • ~q |
اکنون صورت نرمال عطفی ستون ۴ را مینویسیم:
x = (p • q) ∨ (~p • ~q)
این روش، یعنی ساختن فرمول از روی جدول ارزش را میتوان برای هر جدول ارزش دلخواه ثابت کرد. روش اثبات را برای همین جدول دو اتمی نشان میدهیم و همین روش را میتوان برای جدول nاتمی (با ۲n سطر) تعمیم داد.
برای هر گمارش ارزش (یعنی در هر سطر) که مقدار ارزش x درست است مقدار ارزش ترکیب عطفی به دست آمده برای این سطر نیز درست است، زیرا اگر در این ترکیب عطفی مقدار گمارش اتمی نادرست میبود آنگاه نقیض آن اتم را قرار داده بودایم و اگر درست میبود خود آن اتم را قرار داده بودیم. بنابراین برای این گمارش، صورت نرمال فصلی به دست آمده درست خواهد بود. اما این ترکیب عطفی برای هر گمارش دیگر نادرست است زیرا حداقل یک اتم آن دارای ارزش نادرست خواهد بود. بنابراین وقتی مقدار ارزش x مطابق جدول نادرست باشد همه فصلهای صورت نرمال فصلی حاصل نادرست خواهند بود.
برای جدول ارزشی که ستون آخر آن برای همه سطرها 'ن' است x را همیشه (p • ~q) میگیریم.
نتیجه:
برای هر جدول ارزش فرمولی در که در آن تنها رابطهای ~, •, ∨ به کار رفته باشند هست که آن را مینویسد. این فرمول میتواند به صورت نرمال (عطفی یا فصلی) باشد.
■ مثال. (فرمول تعیین اکثریت)
میخواهیم فرمول x را بیابیم آن گونهای که فقط از سه اتم تشکیل شده و بعلاوه مدلهای آن تعبیرهایی باشد که در آنها به اکثریت اتمها مقدار ارزش درست گمارده باشد.
| s تابع گمارش | ۱ | ۲ | ۳ | ۴ | ۵ |
| تعبیر(ها) | p | q | r | (x)I | صوتهای عطفی |
| I۱ | د | د | د | د | p • q • r |
| I۲ | د | د | ن | د | p • q • ~r |
| I۳ | د | ن | د | د | p • ~q • r |
| I۴ | د | ن | ن | ن | ε |
| I۵ | ن | د | د | د | ~p • q • r |
| I۶ | ن | د | ن | ن | ε |
| I۷ | ن | ن | د | ن | ε |
| I۸ | ن | ن | ن | ن | ε |
اکنون صورت نرمال عطفی را با توجه به ستون ۵ مینویسیم و خواهیم داشت:
x = (p•q•r) ∨ (p•q•~r) ∨ ( p•~q•r) ∨ (~p•q•r)
■ تمامیت رابطهای تابع ارزشی
تعریف. تمامیت گویاگر / Expressive Completeness (نیز تمامیت کارکردی / Expressive Completeness):
مجموعهای از رابطهای تابع-ارزش را بگونه گویاگر تمام گوییم اگر و تنها اگر هر جدول ارزش را بتوان با آنها ساخت.
■ قضیه: تمامیت گویاگر رابطها
قضیه. هر یک از مجموعههای:
{~, •}، {~, ∨} و {~, ⊃}
مطابق تعریف تمامیت گویاگر تمام هستند.
اثبات:
یکم؛ از برگردانی به صورت نرمال میدانیم که هر جدول ارزش توسط {~, •, ∨} قابل ساختن است و دوم؛ توتولوژیهای زیر اثبات را به پایان میرساند:
۱. (A • B)  ~(~A ∨ (~B)),
~(~A ∨ (~B)),
۲. (A • B)  ~(A ⊃ (~B)),
~(A ⊃ (~B)),
۳. (A ∨ B)  ~A ⊃ B.■
~A ⊃ B.■
:☚
مجموعه {⊃, •, ∨} بگونه گویاگر تمام نیست.
■ معرفی دو رابط جدید
دو رابط تابع-ارزش '↓' (نفی الزامی / Joint denial) و '↑' (نفی اختیاری / Alternative Denial) را مطابق جداول ارزش زیر معرفی میکنیم.
|
| ||||||||||||||||||||||||||||||||||||
| جدولهای ارزش رابطها '↓' و '↑'. | |||||||||||||||||||||||||||||||||||||
■ قضیه: تمامیت گویاگرانه {↓} و {↑}.
قضیه: هر یک از دو مجموعه {↓} و {↑} دارای تمامیت کارکردی هستند.
اثبات:
با توجه به توتولوژیهای زیر قضیه ثابت شده است.
۱. (~A)  (A ↓ A),
(A ↓ A),
۲. (A • B)  (( A ↓ B ) ↓ (A ↓ B)),
(( A ↓ B ) ↓ (A ↓ B)),
۳. (A ∨ B)  (( A ↑ B) ↑ (A ↑ B)).■
(( A ↑ B) ↑ (A ↑ B)).■
در زیر جدول ارزش برای توتولوژی ۱ در بالا آمده است.
| p | ~p | p ↓ p | (~p)  (p ↓ p) (p ↓ p) |
| د | ن | ن | د |
| ن | د | د | د |
از این قضیه بر میآید که هر فرمول منطق گزارهای (کلاسیک) را میتوان فقط با رابط ↓ یا ↑ نوشت. البته در این صورت، خواندن آنها برای انسان گرچه دشوار است ولی همان طور که یادداشتهای بعد خواهیم دید، انتخاب یکی از این دو به عنوان عنصر پایه در مدل فیزیکی کارگشا است.
■ قضیه: ↓ و ↑ انجمنی نیستند.
قضیه: رابطهای ↓ و ↑ ویژگی انجمنی تمامیت کارکردی هستند.
اثبات:
تعبیرهای زیر قضیه را ثابت میکند.
| p | q | r | p ↓ q | q ↓ r | (p ↓ q) ↓ r | p ↓ (q ↓ r) |
| ن | ن | د | د | ن | ن | د |
| p | q | r | p ↑ q | q ↑ r | (p ↑ q) ↑ r | p ↑ (q ↑ r) |
| د | د | ن | ن | د | د | ن |
■ قضیه: انحصار رابطهای دوتایی ↓ و ↑.
قضیه: تنها رابطهای دوتایی ↓ و ↑ هستند که هر یک به تنهایی تمامیت کارکردی هستند.
اثبات:
فرض کنید '⋈' یک رابط دوتایی باشد که به تنهایی تمام است. میخواهیم جدول ارزش آن، یعنی جدول ارزش:
p ⋈ q
را تشکیل دهیم. بنابراین سطرها و ستونهای راهنمای جدول را تشکیل میدهیم:
| تعبیر(ها) | p | q | p ⋈ q |
| I۱ | د | د | |
| I۲ | د | ن | |
| I۳ | ن | د | |
| I۴ | ن | ن |
(آ). اگر
(p ⋈ q)I۱ = د
آنگاه تعبیر هر فرمول به ازای هر گمارش درست برای همه اتمهای آن درست خواهد بود. در این صورت فرمول ~p برحسب ⋈ تعریف پذیر نخواهد بود. پس باید
(p ⋈ q)I۱ = ن
باشد. بنابراین در سطر اول مقدار ارزش ن را میگذاریم.
(آ.۱). به همین ترتیب
(p ⋈ q)I۴
باید نادرست باشد (چون در غیر این صورت تعبیر هر فرمول به ازای هر نسبت دهی نادرست برای همه اتمها آن نادرست برآورد خواهد شد). بنابراین در سطر چهارم مقدار ارزش د را میگذاریم.
(ب). اگر برای
(p ⋈ q)I۳ و (p ⋈ q)I۲
هر دو مقدار ارزش 'د' برآورد شود آنگاه ⋈ همان ↑ خواهد شد و اگر برای هر دو مقدار ارزش 'ن' برآورد شود آنگاه ⋈ همان ↓ خواهد شد.
(ج). اگر برای
(p ⋈ q)I۳ و (p ⋈ q)I۲
به ترتیب مقادیر ارزش 'ن' و 'د' بر آورد شود آنگاه _ p⋈q منطقاً با ~p همارز خواهد شد (فارغ از آن چه که به q نسبت داده شود).
(ج.۱). اگر برای
(p ⋈ q)I۳ و (p ⋈ q)I۲
به ترتیب مقادیر ارزش 'د' و 'ن' بر آورد شود آنگاه _ p⋈q منطقاً با ~p همارز خواهد شد (فارغ از آن چه که به p نسبت داده شود).■
جدول زیر ثبت مراحل اثبات را نشان میدهد:
| تعبیر(ها) | p | q | p ⋈ q | |
| I۱ | د | د | ن | ن |
| I۲ | د | ن | ن | د |
| I۳ | ن | د | د | ن |
| I۴ | ن | ن | د | د |
■ صورتهای نرمال (Normal Forms)
■ لیترال (Literal)
به یک اتم یا نقیض آن یک لیترال (Literal) میگوییم. برای نمونه p, ~p, q و مانند آنها لیترال هستند.
■ صورت فصلی محض (Pure Conjunctive Form)
به فرمولی با صورت `F۱ ∨ F۲ ∨ ...∨ Fn` که در آن هر Fi یک لیترال باشد یک صورت فصلی محض میگوییم. (n عدد طبیعی بزرگتر از صفر).
مثال:
p • ~q • s
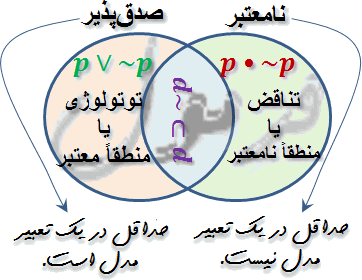
■ صورت نرمال عطفی (Conjunctive Normal Form)
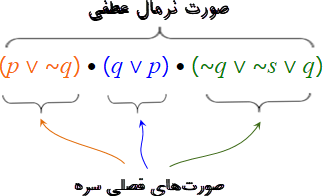
به فرمولی با صورت
A۱•A ۲• . . . •Am
به قسمی که در آن هر Ai صورت فصلی محض باشد یک صورت نرمال عطفی (Conjunctive Normal Form /CNF) میگوییم (m عدد طبیعی بزرگتر از صفر).
مثال:
(p ∨ ~q) • (q ∨ p) • (~q ∨ ~s ∨ q)
در این مثال m = ۳ است و صورتهای فصلی محض به قرار زیر هستند:
A۱: (p ∨ ~q), A۲: (q ∨ p), A۳: (~q ∨ ~s ∨ q).
■ صورت عطفی محض (Pure conjunctive form)
به فرمولی با صورت
F۱ • F۲ • ...• Fn
که در آن هر Fi یک لیترال باشد یک صورت عطفی محض میگوییم. (n؛ عدد طبیعی بزرگتر از صفر).
■ صورت نرمال فصلی (Disjunctive Normal Form)
به فرمولی با صورت
A۱∨A۲∨ . . . ∨Am
به قسمی که در آن هر Ai صورت عطفی محض باشد یک صورت یک صورت نرمال فصلی (Disjunctive Normal Form /DNF) میگوییم. (m؛ عدد طبیعی بزرگتر از صفر).
برای مثال صورت:
(p • ~q) ∨ (q • p) ∨ (~q • ~s)
یک صورت نرمال فصلی است که در آن
A۱: (p • ~q), A۲: (q • p), A۳: (~q • ~s)
صورتهای عطفی محض هستند.
■ روند برگردان صورت گزارهای به صورت نرمال
هر فرمول گزارهای قابل برگردان به صورتهای نرمال عطفی و فصلی است. روند زیر که به آسانی میتوان کارآمد بودن آن را نشان داد، این برگران (برگردانی به صورت نرمال) را ممکن میکند:
۱.
با کارزدن همارزیهای مادی و استلزام مادی رویدادهای رابطهای '≡' و '⊃' در فرمول را حذف کنید.
۲.
با کارزدن چرخهای نفی دوگانه و قضایای دمورگان رویدادهای رابط '~' در فرمول را به بلافاصله قبل از اتمها ببرید.
۳.
مثال:
▢
≡
≡
≡
≡
(p v ~q) ⊃ r
~(p ∨ ~q) ∨ r
(~p • ~(~q)) ∨ r
(~p • q) ∨ r
(p ∨ ~q) • ~r
مثال:
▢
≡
≡
≡
≡
≡
≡
≡
≡
≡
(p • (q ⊃ r) ⊃ s)
(p • (~q ∨ s)) ⊃ s
~(p • (~q ∨ s)) ∨ s
(~p ∨ ~(~ q v r )) ∨ s
(~p ∨ ( q • ~r)) ∨ s
((~p ∨ q) • (~p ∨ ~r)) ∨ s
s ∨ ((~p ∨ q) • (~p ∨ ~r))
(s ∨ (~p ∨ q) • (s v (~p ∨ ~r))
(s V ~p V q) • (s V ~p V ~r)
(~s • p • ~q) V (~s • p • r)
دو یادداشت:
■ یادداشت ۱: کارآمدی استنتاج سمانتیکی
روند تعبیر در منطق گزارهها یک روند کارآمد است. به این معنی که روش جدول ارزش، روندی را در اختیار میگذارد که بهوسیله اجرای آن، ماشین میتواند درباره اعتبار یک استنتاج سمانتیکی دلخواه تصمیمگیری و پاسخ آری یا نه را در زمان محدود ارائه کند. اما این روند گرچه کارآمد است (در زمان محدود به پایان میرسد) ولی کارآمدی آن کارآمدی چندجملهای نیست. یعنی:
در روش جدول ارزش، زمان اجرای ماشینی الگوریتم بر حسب تعداد متغیرهای گزارهای متمایز در استنتاج معنایی رشدی نمایی دارد و نه چندجملهای، زیرا تعداد گمارشهای مقادیر ارزش ممکن با افزایش تعداد متغیرها بهصورت `۲^n` افزایش مییابد (نگاه کنید به فصل ۹، قسمت ۷ — رشد جدول ارزش — کتاب درآمد به منطق). از این رو گفته میشود: پیچیدگی رایانشی مسئله جدول ارزش نمایی است.
بطور کلی:
پیچیدگی زمانی:
پیچیدگی زمانی یک الگوریتم، تابعی است که نشان میدهد زمان اجرای الگوریتم، با افزایش اندازه ورودی `n`، چگونه رشد میکند.
بنابراین مسئله جدول ارزش دارای پیچیدگی نمایی است، که آن را با نمادگذاری `O(2^n)` نشان میدهند.
الگوریتمها و به عبارت دیگر، مسالههایی که حل آنها در سرشت خود دارای پیچیدگی نمایی هستند در عمل (اجرای ماشینی توسط کامپیوترهای رایج / کلاسیک) مفید نیستند. زیرا مسائل واقعی که با این الگوریتمها و توسط سریعترین ماشینهای کلاسیک چه در حال و چه آینده اجرا شوند برای به پایان رسیدن (ارائه جواب) بهطور میانگین به زمانی گرچه محدود ولی بیش از طاقت بشری - گیریم که ماشین بتواند نامحدود کار کند - نیاز خواهند داشت. ازاینجهت، در دانش کامپیوتر، اغلب اوقات، مراد از یک الگوریتم کارساز⮫، یک روند کارآمد است که درجه پیچیدگی آن حداکثر چندجملهای باشد.
1. Hromkovič, Juraj. Theoretical Computer Science: Introduction to Automata, Computability, Complexity, Algorithmics, Randomization, Communication, and Cryptography. Springer, 2003 -2011. pg 30.
در علوم کامپیوتر، به مسئلههایی که حل آنها مستلزم منابع محاسباتی با رشد نمایی نسبت به اندازه ورودی است، معمولاً مسئله سخت گفته میشود. برای توضیحی شهودی از مفهوم «مسئله سخت» و ردههای پیچیدگی محاسباتی، «A Short Guide to Hard Problems» در Quanta Magazine را ببینید.
الگوریتمهایی که برای حل مسئلههایی که در سرشت خود دارای پیچیدگی نمایی هستند عموماً برای استفاده در کامپیوترهای معمولی (کلاسیک) کاربردی نیستند. زیرا با افزایش اندازه ورودی، تلاش محاسباتی مورد نیاز برای این الگوریتمها به سرعت از قابلیتهای حتی قدرتمندترین سختافزارهای کلاسیک فراتر میرود و چنین راهحلهایی را برای کاربردهای دنیای واقعی غیرممکن میسازد.
در نمودار زیر - شکل ۳ - چند پیچیدگی-زمانی الگوریتمها نشان دادهشده و مثل این را میتوان برای مقدار حافظه مصرفی نیز در نظر گرفت و از پیچیدگی فضایی صحبت کرد.
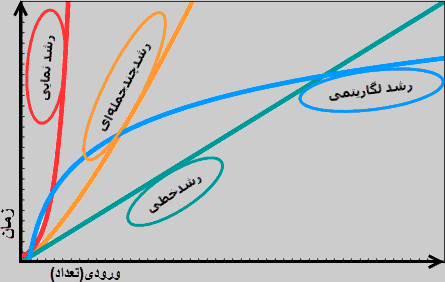
■ یادداشت ۲: کامپیوترهای کوانتمی و پیچیدگی نمایی
احتمالاً بیشتر ما امروزه با نام کامپیوترهای کوانتمی آشنا هستیم. کامپیوترهای کوانتومی از اصول مکانیک کوانتومی⇖ به طور اساسی متفاوت برای پردازش اطلاعات استفاده میکنند. مسائلی که در سرشت فضای جواب نمایی (درجه پیچیدگی نمایی) بدون ساختار قابل بهرهبرداری دارند، حتی برای کامپیوترهای کوانتومی نیز مسائل با درجه پیچیدگی نمایی باقی میمانند. مکانیک کوانتومی به طور جادویی فضای نمایی را ناپدید نمیکند. اما فضای جواب نمایی میتواند دارای ساختار نهفتهای باشد که الگوریتمهای کوانتومی میتوانند از آن برای یافتن جواب بدون کاوش در کل فضای جواب، دستیابی به زمان چندجملهای استفاده کنند. البته، باید توجه داشت که کامپیوترهای کوانتومی یک راه حل کلی «تبدیل مسائل نمایی به چندجملهای» ارائه نمیدهند.

یک فضای جوای با پیچیدگی نمایی را یک هزارتوی وسیع و تاریک تجسم کنید. یک کامپیوتر کلاسیک ممکن است نیاز داشته باشد که هر راهرو را بررسی کند. یک کامپیوتر کوانتومی، اگر هزارتو الگوی پنهان خاصی داشته باشد، میتواند از اثرات کوانتومی برای «حس کردن» خروج بسیار سریعتر استفاده کند. اما اگر هزارتو واقعاً دلخواه و آشوبناک باشد و هیچ الگویی برای بهرهبرداری نداشته باشد، حتی کاوشگر کوانتومی نیز در بررسی بخش قابل توجهی از راهروها گیر میکند.
■ ■ ■ ■ ■

