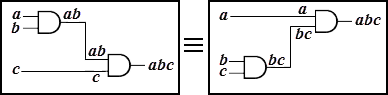جبر بول و مدارهای منطقی

منطق و فرامنطق

درآمد به منطق

روند. جبر بول و مدارهای منطقی

≡

۱- سرآغاز

۱۰- ترانزیستور (Transistors)

۲- جبر بول (Boolean algebra)

۱۱- فیزیک گذرگاه‌های منطقی

۳- هم‌ارزی‌های بولی پرکاربرد

۱۲- بیت (Bit)

۴- ساده گردانی عبارات بولی

۱۳- حافظه

۵- گذرگاه‌های منطقی (Logic Gates)

۱۴- کارکرد حافظه

۶- مدار منطقی (Logic Circuit)

۱۵- ساخت‌کار حافظه

۷- مدار منطقی اکثریت

۱۶- کنترل حافظه یک بیتی

۸- مدارهای منطقی ترکیبی (Combinational logic circuits)

۱۷- مدارهای ترتیبی (Sequential Circuits)

۹- فیزیک مدار منطقی ( دیجیتال / رقمی)

■ سرآغاز

جبر بول (Boolean algebra) که به نام ریاضیدان و منطق‌دان جرج بول نامگذاری شده است، شاخه‌ای از جبر است که با مقادیر درست و نادرست که اغلب به ترتیب با 1 و 0 نشان داده می‌شوند، سروکار دارد. جبر بول بنیاد طراحی منطقی↝ کامپیوتر‌ها و بیشتر سیستم‌های رایانشی مدرن است. در واقع، جبر بول جایی است که منطق به فیزیک پیوند می‌یابد. این قسمت مرور کوتاه جبر بول، تا آنجا که درخور یادداشت قبل↝ باشد، است. ناگفته نماند که جبر خود شاخه‌ای از ریاضیات است که به نمادها و قواعد کار با این نمادها می‌پردازد. نیز با بازنمایی مسئله‌ها↝ یا پیش‌آیندها در قالب عبارت‌های ریاضی درگیر می‌شود.

■ جبر بول (Boolean algebra)

<LC, I> در یادداشت پیشین↝ را به شیوه زیر دستکاری می‌کنیم:

آ.به جای اتم‌های p, q, r, s, t به ترتیب اتم‌های a, b, c, d, e را معرفی کنیم،

ب.ظاهر رابط‌ها • و ∨ به ترتیب رابط‌های × و + را معرفی کنیم [تمامیت کارکردی را ببینبد]،

ج.عالم سخن را مجموعه B برابر {۰, ۱} برای ⇔۱د و ۰ ن⇔) بگیریم،

د. به جای ⏉ و ⏊ به ترتیب 1 و 0 را معرفی کنیم،.

*.آنچه در نشان‌ گذاری نگارشی آمده را رعایت کنیم.

حاصل آ تا د را <LB,|B|,J> می‌نامیم و در این صورت عبارت‌های زیر نمونه‌هایی از فرمول‌های LB هستند.

a , a+b , a+b×c , ~(a+a×c) ≡ a , (a+c)+~d

<LC, I> و <LB,|B|,J> هم ریخت هستند. یعنی، می‌توان نظیر هر عنصر یکی را در دیگری یافت (برای مثال، برای هر تعریف، قضیه یا مانند آن‌ها در یکی معادلی در دیگری وجود دارد).

بعلاوه در <LB,|B|,J> به خاطر آسان نویسی قرارداد می‌کنیم:

(آ.) هر فرمول را به صورت نرمال بنویسیم (با توجه به برگردانی به صورت نرمال این میسر است)،

(ب.) در نوشتن فرمول از لیترال استفاده کنیم (برای مثال a به جای ~a)،

(ج.) مانند عبارت‌های جبر معمولی از نوشتن صریح رابط × وقتی ابهامی نباشد خودداری کنیم.

با توجه به این قراردادها‌ به هر فرمول ‌<LB,|B|,J> یک عبارت بولی و به <LB,|B|,J> یک جبر بول می‌گوییم.

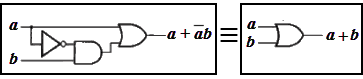
■ هم‌ارزی‌های بولی پرکاربرد

اثبات هم‌ارزی‌های بولی که در زیر آمده و در جبر بول مورد توجه ابتدایی هستند با جدول ارزش به راحتی میسر است:

جدول ۱. هم‌ارزی‌های بولی پرکاربرد
هم‌ارزی منطقی هم‌ارزی بولی

p ∨ ⏉ ≡ ⏉ a + 1 ≡ 1۱.
p ∨ ⏊≡⏉ a + 0 ≡ a ۲.
p • ⏊≡⏊ a × 0 ≡ 0 ۳.
p • ⏉≡⏉ a × 1≡1 ۴.
p ∨ p ≡ ⏉ a + a ≡ a ۵.
p ∨ ~p ≡ ⏉ a + a ≡ 1 ۶.
p • p ≡ p a × a ≡ a ۷.
p • ~p ≡ ⏊ a × a ≡ 0 ۸.
~~p ≡ p a ≡ a ۹.
p ≡ (p•⏉) ≡ (p•(⏉∨q)) ≡ (p•⏉)∨(p•q) ≡ p∨(p•q) ⇒ p∨(p•q)≡p a + a×b ≡ a ۱۰.
a + ab ≡ (a+a)(a+b)
≡ 1×(a+b) ≡ a+b		 ۱۱.
(a+b)(a+c) ≡ aa+ac+ba+bc ≡ a+ac+ba+bc ≡ a(1+c)+ba+bc ≡ a+ba+bc ≡ a(1+b)+bc ≡ a+bc ۱۲.

■ ساده گردانی عبارات بولی

عبارت بولی زیر را در نظر بگیرید،

f: abc+abc+abc+abc.

ساده شده این عبارت بولی ab+bc+ac است. هزینه محاسبه این فرمول سه × و دو + است، حال آنکه هزینه محاسبه f سه متمم‌ (نقیض) گیری، هشت × و سه + است و هر دو نیز مقدار یکسان دارند. برخی روندهای الگوریتمیک برای ساده کردن عبارت‌های بولی [از جمله جدول کارنو /Karnaugh map] برای عبارت‌های شامل تا ۴ متغیر و الگوریتم کواین-مگ کلاسکی /Quine–McCluskey algorithm برای متغیرهای بیشتر] وجود دارد. اما الگوریتمی که هر عبارت بولی را به گونه بهینه ساده کند از جمله مسئله‌های موسوم به NP (Nondeterministic Polynomial) است. مسئله‌های NP را در یادداشت‌های نظریه رایانش توضیح خواهیم داد. اینجا و به عنوان پاسخ کوتاه، مسئله‌های NP مسئله‌هایی هستند که گرچه درستی پاسخ آن‌ها را می‌توان بطور کارساز سنجید، اما روند حل آن‌ها می‌تواند کارساز نباشد. بنابراین، گرچه هر مسئله کارساز یک NP است ولی ورارون آن برقرار نیست.

■ مثال ۱.

عبارت بولی ab + ac + bc را ساده کنید.
ab + ac + (a+a)bc ab + ac + bc ≡
ab + a + abc + abc
ab +abc +ac + abc
ab + abc + ac + acb
ab(1 + c) + ac(1 + b)
ab + ac

■ گذرگاه‌های منطقی (Logic Gate)

در بند زندگی‌نامه چارلز ساندرس پیرس یادآوری شد که وی فیزیکی سازی عبارت‌های بولی را پیشنهاد کرده بود. این منجر به آنچه شد که امروزه (طراحی) مدارهای منطقی نامیده می‌شود. قصد ما در اینجا توضیح کوتاه و البته بنیادین طراحی منطقی است. برای این کار می‌باید از گذرگاه‌های منطقی و سپس مدارهای منطقی که از اتصال گذر‌گاه‌ها به دست می‌آید شروع کنیم. مبنای نظری ما در اینجا صورت‌های نرمال و تمامیت کارکردی <LB,|B|,J> است.

برای ما در اینجا، دروازه‌ منطقی (Logical gate) نام دیگری برای جدول ارزش (تابع ارزش) با حداکثر دو متغیر (یا دو ستون راهنما) است و وقتی به لایه فیزیک نزدیک شدیم، متغیر را نیز ورودی نیز می‌نامیم. و اکنون نزدیک به لایه فیزیک هستیم.

ما در صورت‌های نرمال سه رابط ∨ ،• و ~ را داریم که در اینجا به ترتیب آنها را دروازه‌های AND ،OR و NOT می‌نامیم. با این رابط‌ها می‌توان همه عبارت‌های (بولی) را نوشت. نیز دو رابط ↑ و ↓ را داریم که هر یک به تنهایی تمام هستند. این دو رابط آخری را دروازه‌های NAND و NOR می‌نامیم. در شکل زیر کارکرد (تابع ارزش) و نمای شماتیک این رابط‌ها که در این‌جا به آن‌ها گذرگاه‌های منطق می‌گوییم آمده است:

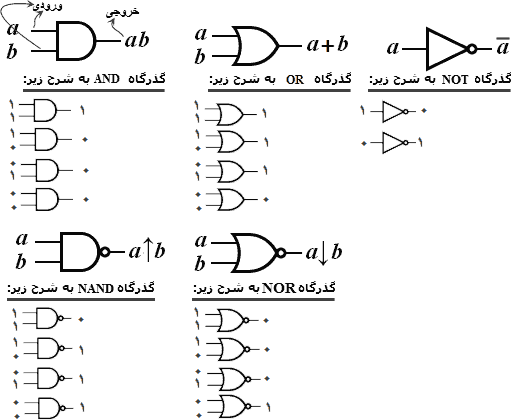
گذرگاه (gate) منطقی
شکل ۱. نمای شماتیک گذرگاه‌های منطقی پایه‌ای (Basic logic gates)

■ مدار منطقی (Logic Circuit)

به نگاره شماتیک یک عبارت بولی یک مدار منطقی می‌گوییم. بنابراین هر یک از گذرگاه‌های منطق در شکل (۱) خود یک مدار منطقی است. مثال‌هایی که در پی خواند آمد خود گویای چیستی مدارهای منطق هستند.

مثال: مدار عبارت بولی: f: abc.

مدار منطقی
شکل ۲. دو مدار بالا با توجه به ویژگی انجمنی دو مدار هم‌ارز هستند.

مثال: دو مدار زیر، دو مدار هم‌ارز هستند. همان‌طور که دیده می‌شود در مدار سمت راست دو گذرگاه صرفه جویی شده است.

مدار منطقی
شکل ۳. دو مدار بالا با توجه به سطر ۱۱ جدول ۱ دو مدار هم‌ارز هستند.

■ مدار منطقی اکثریت

در زیر مدار مثال نمایشگر اکثریت در یک گروه سه نفری آمده است. با هر بار فشار دکمه بازنشان (ریست کردن / resetting سیستم) تمام ورودی‌ها 0 خواهند شد.

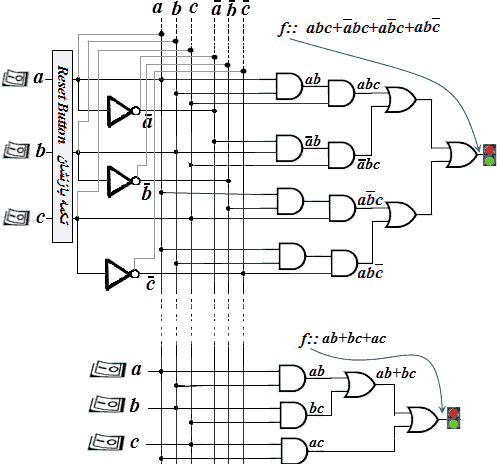
مدار منطقی اکثریت
شکل ۴. مدار منطقی اکثریت. (آ). ساده نشده (ب). ساده شده

■ مدارهای منطقی ترکیبی (Combinational logic circuits)

مدارهای منطقی که تاکنون مورد بحث بود، مدارهای منطقی ترکیبی نامیده (Combinational logic circuit) می‌شوند. علت این نام‌گذاری در واقع تابع–ارزشی بودن آن‌ها است. به عبارت دیگر، خروجی هر مدار (گذرگاه) منحصراً توسط ورودی‌های آن نعیین می‌گردد و نه چیز دیگری. گونه دیگر از مدار‌های منطقی موسوم به مدارهای ترتیبی را در ادامه خواهیم دید.

■ فیزیک مدار منطقی ( دیجیتال / رقمی)

هدف این بند چگونگی اتصال صورت و معنی به زمین است. این اتصال این روزها در سطح کاربردی توسط تکنولوژی نیمه رساناها و ترانزیستور‌ها انجام می‌شود. ترانزیستور یک ابزار بنیادی در الکترونیک و محصول فن‌آوری نیمه‌رسانا‌ها است. نیمه رسانا‌ها موادی هستند که در شرایط خاص رسانای جریان الکتریکسیته هستند و در غیر این شرایط چنین نیستند.

• ترانزیستور (Transistors)

ترانزیستور انواع گوناگون برای مقاصد گوناگون دارد. یک ترانزیستور برای کارکرد خود باید دارای حداقل یک ورودی و یک خروجی جریان باشد. افزون بر آن باید به یک منبع ولتاژ و نیز زمین (زمین در مدارهای الکتریکی حکم سیاه‌چاله‌ای را دارد که می‌تواند همه جریان یک سیستم را در خود فرو دهد) متصل باشد. در شکل زیر (ش.۵) شمای گونه‌ای ترانزیستور موسوم به ترانزیستور دو قطبی (NPN) آمده است.

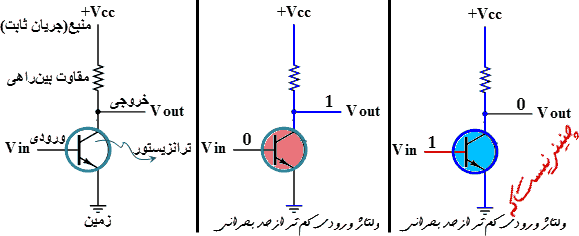
ترانزیستور در مدارهای دیجیتال
شکل ۵. ترانزیستور و کارکرد آن به عنوان معکوس کننده.

کارکرد کلی این ترانزیستور به شرح زیر است:

اگر Vin کمتر از مقدار معینی که به مقدار بحرانی موسوم است باشد (گفته می‌شود در حالت low است، که ما آنرا با 0 نشان می‌دهیم) آنگاه مقدار Vout برابر Vcc (که ما آنرا با 1 نشان می‌دهیم) خواهد بود و می‌گویی ترانزیستور بسته /خاموش است؛

وگرنه (گفته می‌شود در حالت high است (که ما آنرا با 1 نشان می‌دهیم) آنگاه مقدار Vout برابر V0 خواهد بود (که ما آنرا با 1 نشان می‌دهیم) و می‌گوییم ترانزیستور در حالت باز / روشن است.

علت این کارکرد نیز به شرح زیر است:

ماده نیمه رسانا در این ترانزیستور (در واقع، دو نوع متفاوت نیمه‌رسانا، N و P، با آرایش N-P-N) گونه‌ای است که اگر ولتاژ ورودی کمتر از مقدار بحرانی باشد آنگاه ترانزیستور (ماده نیمه رسانا) کاملاً نارسانا خواهد شد (به صورت مقاومت بی‌نهایت عمل می‌کند) و در نتیجه اتصال منبع ولتاژ با زمین قطع خواهد بود و Vcc به Vout جریان می‌یابد. در غیر این صورت ماده نیمه رسانا به صورت یک سیم (رسانا) عمل می‌کند و تمام جریان منبع، Vcc، به زمین سرریز خواهد شد که نتیجه آن ولتاژ صفر در خروجی، Vout، خواهد بود. در چنین وضعیت به این ترازیستور، معکوس کننده نیز گفته می‌شود.

• فیزیک گذرگاه‌های منطقی

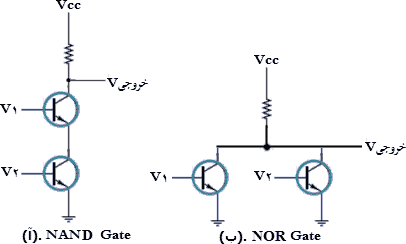
ترانزیستور در مدارهای دیجیتال
شکل ۶. مدل فیزیکی رابط‌های (آ).نفی اختیاری ↓، (ب).نفی الزامی ↑

همانطور که در شکل ۶ در بالا دیده می‌شود بستن سری دو ترانزیستور در (آ) مدل الکترونیکی ↑ و بستن موازی دو ترانزیستور در (ب) مدل الکترونیکی ↓ را به دست می‌دهند. و قضیه تمامیت گویایی نیز تمامیت کارکردی هر یک از این دو گذرگاه را به تنهایی گواهی می‌کند.

■ بیت (Bit)

بیت (Bit) در سطح مدارهای منطقی واحد اطلاعات است. یک بیت اطلاعات عبارت است از یک عضو جهان سخن B≡{0, 1}. دو بیت اطلاعات عبارت است از یک عضو،

B×B≡{0, 1} × {0, 1}≡{(0, 0), (0, 1), (1, 0), (1, 1)}.

به همین ترتیب، n بیت اطلاعات عبارت است از یک عضو مجموعه Bn. در بیشتر وقت‌ها به اعضای مجموعه |B۸|≡۲۵۶ یعنی،

از (0, 0, 0, 0, 0, 0, 0, 0) تا (1, 1, 1, 1, 1, 1, 1, 1)

یک بایت / Byte (یا یک بایت ۸ بیتی) گفته می‌شود. یک بیت در سطح فیزیکی خود (الکترونیک / سطح ابزاری / device level) مداری است که نشان دهنده دو حالت متمایز (خاموش و روشن، سیاه و سفید یا مانند آنها) است. در نمودار مدار اکثریت هر یک از ورودی‌ها و خروجی‌ها و نیز هر خط انتقال (Bus) دربردار یک بیت هستند. بنابراین می‌توان گفت این مدار دارای یک خط انتقال اطلاعات سه بیتی است.

■ حافظه

حافظه یک مدار منطقی است به ‌گونه‌ای که بتواند یک بیت اطلاعات با قابلیت بازیابی و بازنویسی را در خود ذخیره (به شرحی که می‌آید) نماید. در شکل زیر، ش.۷، شمای یک حافظه یک بیتی آمده است. در بند بعدی به کارکرد و کارساخت آن می‌پردازیم.

حافظه تک بیتی
شکل ۷. در این نمودار محیط عامل محیطی است که در آن فقرات اطلاعات تولید و نیز مصرف می‌شود.

■ کارکرد حافظه

۱. حالت آ.

اگر ورودی S مقدار 1 را بگیرد (نشانده / Set شود) فارغ از آنکه در ورودی R چه مقداری است آنگاه مقدار خروجی B برابر 1 و مقدار خروجی A برابر مقدار قبلی خروجی B شود و بعلاوه در این حالت پایدار بماند. یعنی اگر بعداً مقدار S به 0 تغییر مقدار خروجی‌ها بدون تغییرباقی می‌مانند.

۲. حالت ب.

اگر ورودی R مقدار 0 را بگیرد (بازنشان / Reset شود) فارغ از آنکه در ورودی S چه مقداری است آنگاه خروجی B مقدار 0 و خروجی A برابر مقدار قبلی خروجی B می‌شود. بعلاوه در این حالت پایدار می‌ماند. یعنی اگر بعداً مقدار ورودی R به 1 تغییر یابد مقدار B (مقدار خروجی) بدون تغییرباقی بماند.

۳.

مدار جز دو حالت (آ) و (ب) در بالا حالت پایدار دیگری نداشته باشد.

اکنون می‌گوییم در حالت (آ) مقدار 1 در مدار ذخیره شده است و از طریق خروجی B قابل بازیابی است و نیز مقدار قبلی آن از طریق خروجی R قابل بازیابی است. به همین ترتیب می‌گوییم در حالت (ب) مقدار 0 در مدار ذخیره شده است و از طریق خروجی B قابل بازیابی است. و نیز مقدار قبلی آن از طریق خروجی R قابل بازیابی است. بعلاوه این حافظه از طریق دو ورودی خود قابل بازنویسی است.

دقت نمایید که این مقدار حافظه از دست رفتنی (volatile / فرار) است. با غیرفعال شدن آن (مدار) اطلاعات آن به گونه غیر قابل بازیابی از بین می‌رود (پاک می‌شود). اما وقتی فعال است هیچ گاه خالی نیست.

■ ساخت‌کار حافظه

شکل پایین، سمت راست (۸.پ) یک مدار منطقی غیر فعال (بدون اتصال به محیط عامل) را نشان می‌دهد که دارای دو ورودی، دو خروجی و دو گذرگاه NOR (نفی الزامی / ↓) است. در این مدار شعبه‌ای از خروجی هر یک از دو گذرگاه‌ به عنوان یکی از ورودهای گذرگاه دیگر به کار گرفته شده است. در ضمن، جدول ارزش NOR برای آسانی رجوع در زیر آن آمده است.

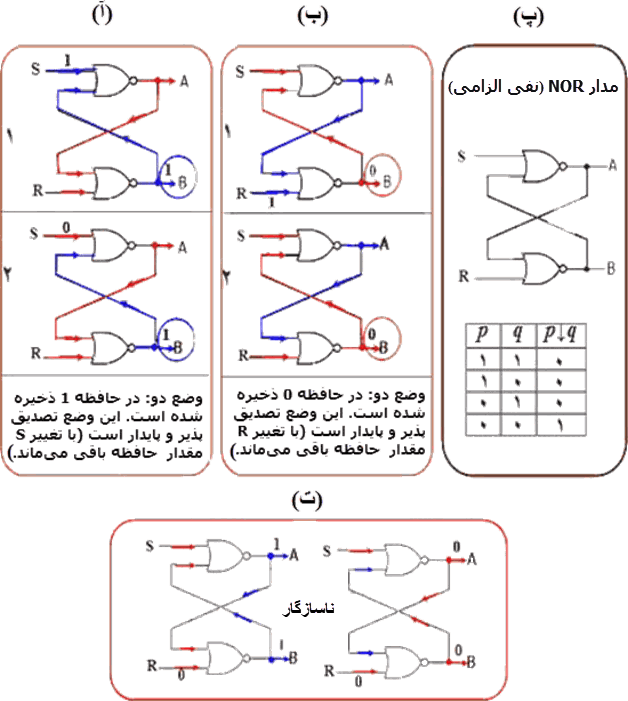
ساخت کار حافظه
شکل ۸. ساخت کار و کارکرد حافظه یک بیتی.

فرض کنید پس از نصب حافظه به محیط عامل ورودی‌ و خروجی‌ها مطابق شکل ۸.آ باشند. با مراجعه به جدول ارزش در می‌یابیم این وضعیت که در آن خروجی B برایر 1 است ممکن (تصدیق‌پذیر) است. می‌گوییم مدار در این حالت در وضع یک است و 1 در آن ذخیره شده است. این وضع (خروجی 1 برای B) نسبت به تغییر S پایدار است، زیرا اگر S تغییر کند (0 شود) B بدون تغییر خواهد ماند (مقدار حافظه تغییر نمی‌کند). شکل ۸.آ.۲ مدار را بعد از تغییر S به 1 نشان می‌دهد.

حالا فرض کنید در این وضع (وضع یک) مقدار R تغییر کند (1 شود)؛ در این صورت مدار به حالت ۸.ب.۱ در خواهد آمد که نسبت به خروجی‌ها در وضعیت جدیدی است. این وضع مدار را وضع صفر می‌نامیم و می‌گوییم 0 در آن ذخیره شده است. این وضع (خروجی 0 برای B) نسبت به تغییر R پایدار است، زیرا اگر R تغییر کند (0 شود) بدون تغییر خواهد ماند (مقدار حافظه تغییر نمی‌کند). شکل ۸.ب.۲ مدار را بعد از تغییر R به 1 نشان می‌دهد.

در هر یک از این دو وضع یک بیت اطلاعات در این مدار (حافظه یک بیتی) ذخیره شده است و مقدار آن از طریق خروجی B قابل بازیابی است و نیز می‌توان توسط ورودی‌ها آن را بازنویسی کرد. یعنی، با ۱ کردن S (موسوم به نشاندن / Set) فقره 1 را در آن نوشت و با 1 کردن R (موسوم به بازنشاندن / ReSet) فقره 0 را در آن نوشت).

افزون بر آنچه گفته شد، در هر یک از این دو حالت تصدیق پذیر مقدار یکی از دو خروجی متمم (نقیض) دیگری است. بنابراین اگر بجای B متغیر q را قراردهیم آنگاه A را می‌توان q نوشت، یعنی خروجی A مقدار حافظه را قبل از آخرین تغییر نشان می‌دهد.

■ کنترل حافظه یک بیتی

برای کنترل ساخت‌کار حافظه، به شرحی که می‌آید، یک الحاقیه مداری مطابق شکل ۹ به آن می‌افزایند:

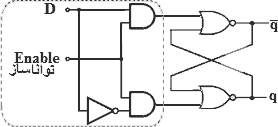
توانا ساز حافظه
شکل ۹. تواناساز حافظه

در این مدار اگر تواناساز غیرفعال باشد (0 باشد) تغییر D موجب تغییر محتوی حافظه نمی‌شود، در غیر این صورت ورودی D هرچه باشد در حافظه ذخیره می‌شود. برای توضیح بیشتر به نمودار ۸.آ.۱ و ۸.ب.۱ توجه نمایید.

■ مدارهای ترتیبی (Sequential Circuits)

اگر به مدار‌های شکل.ط.۴ نگاه کنیم پی می‌بریم که یکی از ورودی گذرگاه‌ها با یک واسطه خروجی همان گذرگاه است. این یعنی، خروجی کل مدار صرفاً به ورودی‌‌های گذرگاه‌های آن در حال فعلی وابسته نیست، بلکه به خروجی آن‌ها (مقدار قبلی ورودی‌ها) نیز می‌تواند وابسته باشد. چنین مدارهایی را مدارهای ترتیبی (در مقابل مدارهای ترکیبی که چنین نیستند) می‌گویند.

در بند از مدل به فرمول دیدیم که چگونه از روی جدول ارزش می‌توان فرمول تولید کننده آن جدول ارزش را تشکل داد و سپس ساده و آن را رسم کرد. در مورد مدارهای ترتیبی این روش ممکن نیست زیرا در این مدارها خروجی صرفاً تابع ورودی‌ها در حال فعلی نیست. برای طراحی مدارهای ترتیبی روش‌های دیگری را به کار می‌بندند که بیرون از زمینه کار ما است.

◄ توجه: