۱۰.پیوست ۱: برهان شرطی و قضیه در منطق گزارهای
برهان شرطی یک روش اثبات برای استدلالهای استنتاجی، آن استدلالها که معمولاً بهصورت گزاره شرطی (اگر ... آنگاه) بیان میشوند، است که همچون یک قاعده استنتاج در ساختن برهان صوری اعتبار بکار بسته میشود.
☚: در ویرایشها پیشین (پیش از ویرایش ۱۵) بحث برهان شرطی در کتاب «درآمد به منطق» نبود و از این جهت برگرداننده این قسمت و بعدی آن را فراهم آورده بود. اکنون که در ویرایش پانزده «برهان شرطی» به «کتاب» افزوده شده است میتوان از این قسمت گذشت.
طبق قاعده برهان شرطی، برای یک گزاره بفرض «A⊃B»، ابتدا مقدم شرطی مورد اثبات، یعنی A، از آن مجزا و بعنوان یک مقدمه فرضی درست فرض میشود. سپس بناشده بر این مقدمه فرضی، تالی شرطی مورد اثبات، یعنی B، باکار زدن دیگر قواعد استنتاج از آن بهعنوان میان-نتیجه استخراج میشود. سر آخر، مقدمه فرضی و نتیجه دستآمده با رابط استلزام مادی ترکیب میشود.
برای مثال، برای آوردن برهان برای گزاره "اگر در مثلثی دو نیمساز مساوی باشند آنگاه دو ضلع در آن مثلث مساوی هستند" به شیوه برهان شرطی، ابتدا مقدم یعنی، "مثلثی با دو نیمساز مساوی وجود دارد" از صورت استدلال جدا و فرض گرفته میشود. سپس مساوی بودن دو ضلع این مثلث مفروض، مطابق قواعد هندسه از مقدم جداشده استخراج میشود. سر آخر "مثلثی با دو نیمساز مساوی وجود دارد" و "دو ضلع در این مثلث مساوی هستند" با رابط استلزام مادی "اگر ... آنگاه" ترکیب میشوند.
در ادامه این یادداشت علاوه بر شرح مفصل برهان شرطی به مفهوم قضیه در منطق جدید و نیز رابطه بین برهان شرطی و برهان غیرمستقیم نگاه خواهیم کرد.
آ.۱ برهان شرطی:
دستگاه استنتاج طبیعی را که در فصل دهم کتاب گسترانده دستگاهی تمام ولی دارای افزونگی است. اما، اگر بعض قواعد استنتاج از فهرست قواعد ۱۹گانه حذف شود آنگاه دیگر دستگاه تمام نخواهد بود. برای مثال اگر قاعده ششم استنتاج یعنی قاعده جذب از فهرست قواعد حذف شود آنگاه میتوان نشان داد که برای استدلال:
A ⊃ B / ∴ A ⊃ (A • B)
صرفاً با کار زدن بقیه قواعد استنتاج نمیتوان یک برهان صوری اعتبار تشکیل داد. استدلال بالا خود یک مورد قاعده جذب است و بنابراین معنای دیگر آنچه گفته شد این است که قاعده جذب برخلاف قیاس اقترانی در دستگاه ۱۹ قاعدهای از بقیه قواعد قابل استنتاج نیست. به این ویژگی یک قاعده دریک دستگاه استنتاجی معین، نابستگی قاعده استنتاج در آن دستگاه میگویند. بهعبارتدیگر، یک قاعده استنتاج را در یک دستگاه استنتاجی نابسته گویند اگر و فقط اگر از بقیه قواعد دست نیامدنی باشد➥.
در اینجا فرض میکنیم که قاعده جذب در فهرست قواعد استنتاج دستگاه ۱۹قاعدهای کتاب حضور ندارد ولی بقیه قواعد مانند سابق در فهرست حاضرند. میخواهیم با معرفی یک روش، موسوم به روش برهان شرطی، تمامیت را برای این دستگاه جدید برقرار سازیم. چند پاراگراف پایینتر دلیل این کار را نیز میگوییم.
کار را با استدلال بالا آغاز و به شیوه زیر میکوشیم تا نشان دهیم این استدلال معتبر است: میگوییم در استدلال بالا چه پیش میآمد اگر A درست بود؟ (البته ما این را نمیدانیم و این بعنوان مقدمه در مقدمات ما حاضر نیست. اما چه میشد اگر در مقدمات ما بود.) اگر A درست بود آشکارا B نیز درست بود؛ زیرا باکار زدن قیاس استثنائی(.M.P) میتوانستم از A⊃B و A یعنی مقدمهای که فرض کردیم به B برسیم. پس اگر A درست بود، B نیز درست بود و آنوقت بنا بر قاعده پیوست، A•B هم درست بود. بنابراین تا اینجا، نشان دادهایم: اگر A آنگاه (A•B). آن را که نمادین کنیم خواهیم داشت:
A ⊃ (A • B)
و این همان نتیجه استدلال بالا است.
مراد از برهان شرطی (یا قاعده برهان شرطی ) یک قاعده استنتاج است که به موجب آن میتوان یک شرطی را از یک استنتاج که فرض آن مقدم این شرطی و نتیجه آن تالی آن باشد استخراج کرد. در سیاهه برهان به این قاعده با کوتهسازی C.P اشاره خواهیم کرد.
برهانی به این قسم موسوم به برهان شرطی است. در زیر برهان بصورت نمادین آمده است.
[توجه: در این برهان در خط ۲، 'AP' کوتهسازی مقدمه مفروض / Assumed Premise است و عبارت /∴(A•B) سمت راست 'AP' از این جهت است که چه چیز قرار است از این مقدمه فرضی با کاربست قواعد استنتاج (و احتمالاً از مقدمات اصلی) استنتاج شود]:
| /∴ A ⊃ (A • B) | A ⊃ B | ۱. | ||
| AP /∴(A • B) | A | ۲. | ||
| ۱, ۲, M.P. | B | ۳. | ||
| ۲, ۳, Conj. | A • B | ۴. |
آنچه تاکنون دستآمده عبارت است از، اگر A آنگاه (A•B). با تعویض عبارت "اگر... آنگاه ..." با "⊃" خواهیم داشت:
| ۲–۴, C.P. | A ⊃ (A • B) | ۵. |
نکته مهم و مورد توجه اینجاست که نتیجه، یعنی خط ۵، فقط به مقدمه اصلی بستگی دارد و نه به فرض آمده در خط ۲. اگر مقدمه ۱ درست است آنگاه خط ۵ باید درست باشد، چه A (مقدمه فرض شده) درست باشد و چه درست نباشد. خط ۵ نمیگوید (A•B) برقرار است، بلکه میگوید برقراری (A•B) مشروط به برقراری A است. توجیه سمت راست خط ۵ خاطرنشان میکند تکنیک بهکاررفته در اینجا برهان شرطی است که از یک مقدمه فرضی استفاده کرده [ فرض — آن چیزی است که در استدلال اصلی بهعنوان مقدمه نیامده است]؛ و بعلاوه شماره خط شامل مقدمه فرضی و نیز شماره آخرین خطی که به این مقدمه بستگی دارد را فهرست میکند.
برای ثبت سابقه مقدمه (یا مقدمات) فرضشده که میخواهیم با آن برهان را ادامه دهیم و نیز خطهای وابسته به آن از نشان پیکان و خط راست استفاده میکنیم، به قسمی که برهان موردبحث بهصورت زیر درآید:

پیکان اشارهکننده به خط ۲ نشان میدهد که این خط یک مقدمه فرضشده است و بهعنوان بخشی از مسئله اصلی دادهنشده است. خط رسم شده از خط ۲ تا زیر خط ۴ نشان میدهد خطهای ۳ و ۴ وابسته به خط ۲ (و شاید هم به مقدمات اصلی) هستند. در این حالت میگوییم، این خطها (۲ تا ۵) در قلمرو مقدمهِ فرضی هستند. خط افقی بین خطهای ۴ و ۵ نشان میدهد که خطهای بعد از آن به خط ۲ بستگی ندارند؛ بهعبارتدیگر، نشان میدهد که قلمرو مقدمه فرضشده با خط ۴ پایان یافته است. ازاینجا به بعد میگوییم مقدمه فرضشده دیگر یک فرض تخلیه شده است.
با استفاده از نشانهگذاری پیکان و خط که هماکنون معرفی شد میتوانیم ساختار برهان شرطی (یا صورت استدلال) را مطابق زیر بیان کنیم:
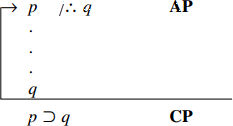
این نشان میدهد که یک مقدمه فرض شده و بقیه خطها از آن بهدستآمدهاند، سپس مقدمه فرضشده، بهعنوان مقدمه، تخلیه و بهعنوان مقدم در خط p⊃q حفظ شده است. با این قاعده میتوان برای قاعده جذب، البته دیگر نه بهعنوان قاعده نابسته بلکه بهعنوان یک صورت استدلال معتبر، یک برهان صوری تشکیل داد و آنوقت مثال بالا موردی از این صورت استدلال معتبر خواهد بود. درنتیجه ازآنجاکه دستگاه ۱۹ قاعدهای کتاب تمام است، میتوان همان اثبات تمامیت اثبات تمامیت را برای این دستگاه جدید نیز بهطور مستقل ارائه کرد.
مثال
هر کاربرد صحیح C.P به هم پیوستن عناصر زیراست:
1. عبارت گزارهای که بهوسیله C.P توجیه میشود باید یک شرطی باشد.
2. مقدم این شرطی باید مقدمه فرض شده باشد.
3. تالی این شرطی باید عبارت گزارهای خط قبلی باشد.
4. خطهای رسم شده نشاندهنده قلمرو مقدمه فرضی باشد.
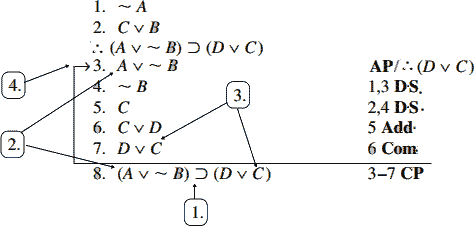
طور دیگر هم میتوان به برهانهای شرطی نگاه کرد. در یک برداشت هر استدلال معتبر یک شرطی است، زیرا درستی نتیجه مشروط بهدرستی مقدماتی است که این نتیجه بدانها وابسته است. آنچه درباره یک برهان موسوم به شرطی متفاوت است فقط این است که بعضی خطها در برهان شرطی وابسته به خطی هستند (مقدمه فرضشده) که نتیجه برهان به آن خط وابسته نیست، یعنی به آن خط که بهعنوان مقدمه در استدلال داده نشده است. هرچند که یک خط بهعنوان یک مقدمه معرفی میشود و یک نتیجه از آن به دست آورده میشود(در رابطه با سایر مقدمات)، ولی بعداً این مقدمه بهعنوان یک مقدمه تخلیه میشود(یا بهعنوان یک مقدمه پس گرفته میشود)، و در عوض بهعنوان یک شرط پذیرش نتیجه حفظ میشود--بهعبارتدیگر، بهعنوان مقدم در یک نتیجه شرطی جدید حفظ میشود.
مهم است توجه کنیم وقتی یک مقدمه فرضشده تخلیه گردید، دیگر نمیتوان آن و همینطور هر خط وابسته به آن را بکار برد . برای نمونه، در مثال قبل نمیتوانیم بهعنوان خط ۶، عبارت گزارهای ~~(A•B) را از خط ۴ بهوسیله .D.N (نقض مضاعف) به دست آوریم، زیرا هماکنون خط ۲ را بهعنوان مقدمه تخلیه کردهایم. در عمل، همه آنچه از یک برهان شرطی به دست میآید یک خط شرطی، یعنی خط زیر خط رسم شده پائینی، است. البته این خط میتواند بهکفایت، برای آوردن برهان وقتی مراد خود این شرطی نباشد، کلیدی باشد.
اکنون پرسش پیش میآید؛ از آنجا که منطق گزارهها با قواعد نوزدهگانه(به شمول قاعده جذب) با همان برداشت کتاب تمام است چه نیازی به معرفی قاعده برهان شرطی است؟ بخشی از جواب این است که، یک ویژگی C.P همانا توانمندی بسیار زیاد آن در کوتاهتر کردن برهان تعداد زیادی استدلال معتبر است و بهویژه آسانتری در پیدا کردن برهان برای بسیاری از استدلالهای معتبر. در کتاب نیز دو روش برهان غیرمستقیم و تکنیکهای کوتاهتر جدول ارزش به همین دلیل آمده است.
اما مهمترین دلیل برای معرفی C.P انطباق بیشتر دستگاه منطق گزارهها با سیستم استنتاجی طبیعی است. بهعبارتدیگر، میخواهیم این قواعد دربرگیرنده آن قسم از استدلالهایی باشند که برای مثال در ریاضیات مقدماتی و متوسط و یا درواقع در زندگانی روزانه جاری هستند. استدلالهای طبیعی عموماً مفروضاتی را درون خود همراه دارند. ممکن است یک هندسه دان از شما بخواهد وجود یک مثلث را برای اثبات یک درستی عام برای همه مثلثها مفروض بگیرید. یک وکیل میتواند کاملاً معقول از هیئتمنصفه بخواهد برای لحظهای موکل وی را مقصر فرض کنند تا آنچه از این فرض حاصل میشود را نشان دهد. "بنابراین شما آقایان و خانمها ملاحظه میکنید که اگر موکل من آنگونه که دادستان میگوید مقصر باشد، شاهدان اصلی وی حقیقت را درباره آنچه در آن شب گذشت نمیگویند." C.P بدین خاطر تدوینشده تا این روش طبیعی به دست آوردن یک شرطی فراهم شود.
C.P تقریباً در هر قسم حالات مفید است، لیکن بیشترین فایده برای وقتی است که نتیجه استدلال موردنظر شرطی یا نتیجهای که میتواند بهصورت شرطی برگردانده شود، باشد. در زیر یک مثال کلاسیک آمده که C.P در آن بکار زدهشده است.
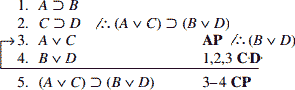
برهان کوتاه و ساده حاصلشده است. برهان بالا را با براهین دیگر این استدلال است که بدون استفاده از C.P ساخته میشوند مقایسه کنید تا تفاوت را مشاهده نمایید. در صورت شک، اعتبار آن را فقط با استفاده از ۱۹ قاعده استنتاج ثابت کنند.
☚: برای مشاهده برهان بدونC.P اینجا را کلیک کنید.
توجه کنید، ما مقدم نتیجه استدلال که یک شرطی است را بهعنوان مقدمه فرضی خود انتخاب کردهایم. هرگاه از قاعده برهان شرطی استفاده میکنید، همیشه مقدم شرطیای را که میخواهید باکاربرد C.P به دست آورید فرض بگیرید.
در مثال بالا فقط یک مقدمه فرضی بکار گرفته شده. اما هر تعداد فرض را میتوان دریک برهان معرفی کرد و البته بهشرط آنکه در پایان همه آنها تخلیهشده باشند. برهان برای همارزیها معمولاً مستلزم دو زیر-برهان جداست، همانطور که در برهان زیر نشان داده شده:

اینجا قسمی از حالت متفاوت آمده است که در آن چند فرض بکار گرفتهشده:
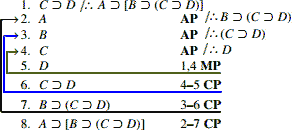
در این مثال سه مقدمه فرضی وجود دارد: A، B، و C. اما خود برهان بسیار ساده است. همه مراحل این برهان بهاستثناء خط ۵، یعنی قدم آشکارای قیاس استثنایی (MP) خودکار است. نیاز نیست تقلای زیاد کرد تا کدام قاعده را بکار برد. بهعنوان یک حساب سرانگشتی، هر جا نیاز است یک شرطی استخراج شود مقدم را فرض بگیرید و سعی کنید تا تالی آن را به دست آورید، به این وسیله مجوز دریافت میکنید تا تمام شرطی را بهوسیله C.P نتیجه بگیرید. در این حالت چون نیاز است [(A⊃[B⊃(C⊃D را نتیجه بگیریم، ابتدا A را فرض گرفته و سعی میکنیم (B⊃(C⊃D را به دست آوریم. دوباره در وضعی هستیم که نیازمندیم تا یک شرطی را نتیجه بگیریم، پس B را فرض گرفته و به سمت C⊃D خواهیم رفت. البته این نیز یک شرطی دیگر است و لذا C را فرض میگیریم و سعی میکنیم D را به دست آوریم- آنچه باقیمانده این است که با یکبار کار زدن MP (قیاس استثنایی) برهان را کامل کنیم.
مقدار زیادی آزادی عمل همراه C.P است. شما میتوانید هر چیزی را فرض بگیرید و البته بهشرط آنکه سرانجام بهطور صحیح آن را تخلیه کنید. نشانهگذاری طوری تدبیر شده تا هر فرض بهطور صحیح تخلیه شود. هر فرض باید با یک پیکان علامتگذاری شود و هر پیکان باید در یک خط افقی پایان پذیرد و هیچ دو خطی نباید همدیگر را قطع کنند.
میتوانید هر چیزی را فرض بگیرید، اما نه همه فرضها سودمند هستند. اینجا یک قاعده سرانگشتی بسیار مهم آمده: در تصمیمگیری برای اینکه چه چیزی را باید فرض بگیرید، راهنما باید نتیجه یا میاننتیجهای باشد که میخواهید به آن برسید و نه مقدمات. برای مثال به برهان زیر توجه کنید:
۱. A ⊃ B
۲. (A ⊃ C) ⊃ D
∴ (B ⊃ C) ⊃ D
با نگاه به مقدمات ممکن است به این فکر افتاد تا A یا A⊃C را فرض گرفت (تا بتوان M.P را بکار بست.) و البته منعی هم نیست تا این فرضها را انتخاب نکرد. اما هر فرض گرفته باید تخلیه شود. برای مثال اگر A را فرض بگیرید آنچه را که سرانجام بعد از تخلیه فرض بهوسیله C.P به دست میآورید یک شرطی است که مقدم آن A است. به همین ترتیب فرض گرفتن A⊃C سرانجام شمارا به یک شرطی خواهد رساند که مقدم آن A⊃Cخواهد بود. هیچکدام از این فرضها شمارا به تکمیل برهان نزدیکتر نخواهد کرد.
آنچه را باید در این برهان بخصوص فرض بگیرید مقدمه نتیجه بهقرار زیر است:
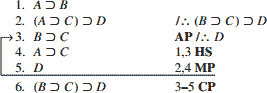
گاهی قبل از آنکه تصمیم بگیرید چه چیزی را فرض کنید اگر از نتیجه برگشت کنید آنوقت موجب میشود برهان خیلی کوتاهتر، آنگونه که در مثال زیر به نمایش درآمده، شود.
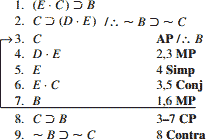
آنچه در این برهان فرض شده نه مقدم نتیجه بلکه مقدم عکس نقیض نتیجه(ترانهش/Trans قاعده 15) است. البته میتوانید برهان را با فرض گرفتن B~ نیز بسازید، ولی اثبات آن بسیار مشکلتر میشود. بنابراین به خاطر بسپارید که گاهی مفید است تا مقدم عکس نقیض نتیجه بجای مقدم نتیجه فرض گرفته شود. (این استراتژی برای ساختن برهانهای منطق محمولات که بحث آن بعد خواهد آمد بهویژه مفید واقع خواهد شد).
به فرضی که درون قلمرو یک فرض دیگر قرار گیرد، فرض تو-در-تو / لانهای / nested میگویند. هماکنون در بالا یک برهان با دو فرض لانهای را مشاهده کردیم. آنچه درباره فرضهای تو-در-تو باید خاطر سپرد اینکه، هر فرض لانهای باید قبل از تخلیه فرض اصلی تخلیهشده باشد. خطهایی که قلمرو فرضهای گرفتهشده را نشان میدهند هرگز نباید همدیگر را قطع کنند.
چنانچه کار را به شیوه برگشت از نتیجه و با کار زدن واگردان(.Exp قاعده ۱۸) آغاز کنید آنگاه میتوانید از گرفتن فرضهای تو-در-تو خودداری و برهان را کوتاهتر کنید. در زیر میتوان برهان کوتاهتر برای استدلال (I) در بالا را مشاهده کرد.
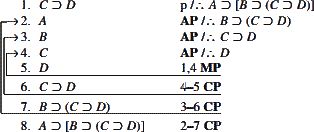
حتی اگر نتیجه یک شرطی نباشد بازهم میتوانید از CP استفاده کنید. اگر نتیجه یک ترکیب فصلی باشد، میتوان باکار زدن استلزام مادی(.Impl قاعده ۱۵) و آغاز با برگشت-از-نتیجه، همارز شرطی نتیجه را بیابید و سپس از CP برای رسیدن به این شرطی استفاده کنید. اگر نتیجه یک دو شرطی است با برگشت-از-نتیجه و کار زدن هم ارزی مادی (.Equiv قاعده ۱۷) دوشرطی را به عطف دو گزاره شرطی برگردانید. سپس CP را جداگانه برای اثبات هر یک از این دو عبارت شرطی بکار ببرید. این دو استراتژی در مثالهای زیر نمایش دادهشدهاند.
مثال. قدمبهقدم برای کار زدن قاعده برهان شرطی:
میخواهیم برای استدلال زیر با استفاده از CP یک برهان بیاوریم. برهان این استدلال را نیز صرفاً باکار زدن قواعد فهرست(بدون قاعده جذب) نمیتوان آورد.
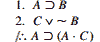
ابتدا به نتیجه استدلال نگاه میکنیم و مقدم آن را فرض میگیریم. سپس به سمت به دست آوردن تالی آن پیش میرویم:

اکنون دیگر تکمیل برهان سرراست است:

پسازآنکه به کار زدن C.P عادت کردید آن را خیلی آسان خواهید یافت و اینکه چه وقت باید آن را کار زد بسیار آشکار خواهد بود. در اینجا مثال دیگری است که کمی بهظاهر سختتر مینماید:
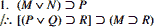
ابتدا به نتیجه استدلال نگاه میکنیم و مقدم آن را فرض میگیریم. سپس به سمت به دست آوردن تالی آن پیش میرویم:
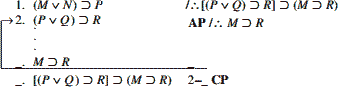
هنوز نیاز است تا شرطی دیگری را به دست آورد، بنابراین فرض دیگری را گرفته:

شایان توجه است که درواقع ما یک برهان یک-مقدمهای مشکل را به یک برهان سه-مقدمهای بسیار آسان برگرداندیم. آنچه باقی است کار زدن قاعده افزایش(.Add/قاعده ۹) است:

چند مثال که در آنها قاعده برهان شرطی به کار بستهشده است:
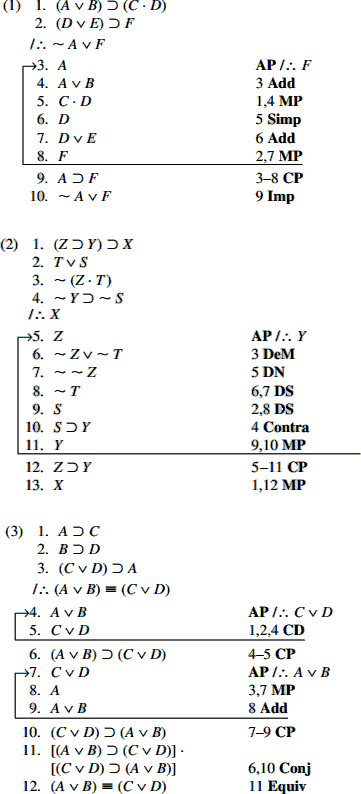
آ.۳. قضیه در دستگاه استناجی:
به برهان معتبر زیر (در دستگاه جدید) که در آن قاعده برهان شرطی بهکاررفته توجه کنید.
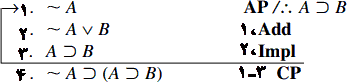
نتیجه این برهان معتبر، عبارت گزارهای ~A⊃(A⊃B) است. اما این عبارت نتیجه چه استدلال و بهعبارتدیگر نتیجه چه مقدماتی است؟ آشکارا، همانطور که در صورت برهان میتوانید ببینید، عبارت گزارهای بهدستآمده نتیجه هیچ مقدمهای نیست(در واقع نتیجه صفر مقدمه است.) اگر به قبل از خط ۱ در برهان بالا هر تعداد مقدمه دلخواه بیفزایید بازهم برهان معتبر باقی خواهد ماند. بهعبارتدیگر، عبارت گزارهای ~A⊃(A⊃B) نتیجه هر مقدمهای است. به چنین عبارتهای گزارهای قضیه گفته میشود. بعلاوه، بهوسیله جدول ارزش میتوان آزمود و دید که این عبارت گزارهای یک توتولوژی است.
☚ در متون فارسی منطق ارسطویی مراد از "قضیه" - "گفتاری (جمله تمامی) است که میتواند متصف به صدق و کذب شود." بنابراین، همانطور که دیده میشود، "قضیه" در منطق جدید از بنیاد چیزی دیگر است.
توجه نمایید که توتولوژی و قضیه دو مفهوم نگاری از آن چیزی است که به صدق منطقی موسوم است. توتولوژی یک مفهوم معنایی است. یعنی، یک توتولوژی به طور معنایی (سمانتیکی) بر پایه جداول ارزش صادق است؛ به عبارت دیگر، مقدار ارزش آن (سمانتیک آن / معنای آن) فارغ از آن که مقدار ارزش گزارههای مؤلفهای آن چه باشد درست است. ولی قضیه یک مفهوم نحوی (تألیف لفظی) است. یعنی، مطابق قواعد استنتاج مشخص، که خود نحوی هستند، و نابسته به هیچ مقدمهای دست آمدنی / drivable است.
اگر یک دستگاه استنتاجی دارای این خاصیت باشد که در آن هر قضیه یک توتولوژی نیز باشد، آنگاه آن را یک دستگاه استوار مینامند.
اگر یک دستگاه استنتاجی دارای این خاصیت باشد که در آن هر توتولوژی یک قضیه نیز باشد، آنگاه آن را یک دستگاه تمام مینامند.
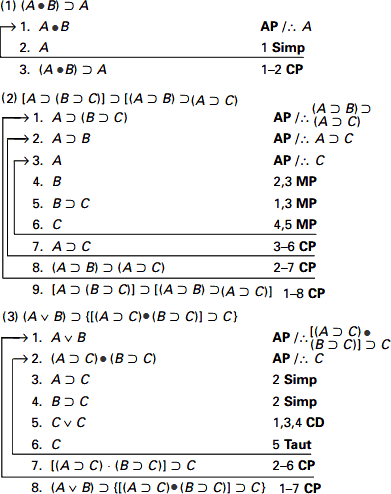
چند مثال از قضیه که در آنها قاعده برهان شرطی به کار بستهشده است:

☚ این قسمت با اندک تغییر، به خاطر پیوستگی، برگرفته از
Alan Hausman, Howard Kahane, Paul Tidman , "Logic and Philosophy: A Modern Introduction" , Hackett Publishing Company, Inc.; Thirteenth edition (February 24, 2021)
است.
◄ توجه: ➥
در زیر است.

