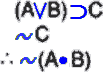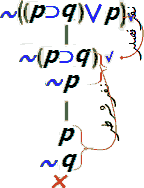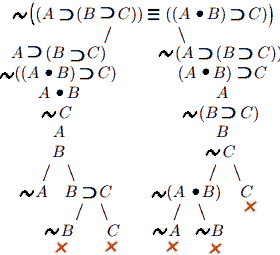درخت صدق (معنا) و الگوریتم آن
روشهای استنتاج
درآمد به منطق فصل ۱۰ پیوست ۳
تاکنون برای اثبات اعتبار یا بیاعتباری یک استدلال تابع-ارزش روشهای جدول ارزش، جدول ارزش کوتاهتر و برهان صوری اعتبار را مشاهده کردهایم. این قسمت معرفی روش «درخت صدق» (نیز «درخت ارزش»، «درخت معنایی» یا «روش تابلو») همچون یک سازواره ماشینییِ آزمون اعتبار (و بیاعتباری) استدلال است. ورودی در این روند یک صورت استدلال و خروجی آن یک «ساختار درختی» است که در آن اعتبار (یا بیاعتبار) استدلال مورد آزمون به نمایش درآمده است.
۱۰.پ۳. درخت صدق (معنا) و الگوریتم آن
تاکنون برای اثبات اعتبار یا بیاعتباری یک استدلال تابع-ارزش روشهای جدول ارزش، جدول ارزش کوتاهتر، برهان صوری اعتبار را مشاهده کردهایم. از میان این روشها فقط روشهای جدول-ارزش بود که سازواره (ماشینی) برای تصمیمگیری در باره اعتبار یا بیاعتباری یک استدلال تابع-ارزش فراهم میکرد. و البته دیدیم که تکنیک جدول-ارزش کامل، دارای این کاستی است که با افزایش تعداد گزارههای استدلال گرفتار رشد ادارهنشدنی میگردد و تکنیک جدول ارزش کوتاهتر گرچه کارساز، اما تنها برای استدلالهای تابع-ارزشی کارزدنی است.
■ درخت صدق
روشی که برای اعتبارسنجی استدلال در اینجا خواهد آمد و به درخت صدق (درخت معنا، روش تابلو) موسوم است کاستیهای گفتهشده در بالا را ندارد و از جمله کارآمدترین (پیچیدگی چندجملهای) در این زمینه است. بنابراین، مراد از درخت صدق یک الگوریتم کارساز، آنگونه که خواهیم دید، برای آزمون اعتبار استدلال است. درواقع، این روند (درخت صدق) فصل مشترک جدول-ارزش و آنچه برهان صوری اعتبار نامیده شد است. بنمایه روش درخت صدق آنچه در (ب).۹. ۱.۰ زیر عنوان "لم درخت" آمده، است. در زیر برای یادآوری آن را مرور میکنیم. پیش از رفتن به پارگراف بعد نگاه دوبارهای به تناظر بین صورت استدلالی معتبر و توتولوژی در قسمت ۸ فصل ۹ (بند-د) داشته باشید.
■ مبنای روش درخت صدق در آزمون اعتبار استدلال
شمای صورت استدلال (A۱) در زیر را در نظر بگیرید:
(A۱):
مقدمه-۱
مقدمه-۲
. . .
. . .
مقدمه-n
/∴ نتیجه
اکنون مجموعه زیر، یعنی مجموعه مقدمات ۱ تا n و نقیض نتیجه شمای صورت استدلالی بالا، را در نظر بگیرید.
(A۲): {,~نتیجه ,مقدمه-n ,. . . , مقدمه-۲ ,مقدمه-۱}
۱- اگر شمای صورت استدلال (A۱) معتبر باشد آنگاه ترکیبی از مقادیر ارزش وجود ندارد که همه مقدمات ۱ تا n را درست سازد (برای آنها مدل باشد) و نتیجه را نادرست سازد (مدل نتیجه نباشد). پس ترکیبی از مقادیر ارزش وجود ندارد که مقدمات و نقیض نتیجه، یعنی مجموعه شمای صورتهای گزارهای (A۲)، را درست سازد. این یعنی (A۲) ناسازگاری است.
۲- اگر مجموعه (A۲) ناسازگار باشد آنگاه ترکیبی از مقادیر ارزش وجود ندارد که همه مقدمات ۱ تا n را درست و نقیض نتیجه را درست سازد (اگر چنین باشد (A۲) ناسازگار نیست که خلاف فرض است). این یعنی، ترکیبی از مقادیر ارزش وجود ندارد که مقدمات ۱ تا n را درست و نتیجه را نادرست سازد. بنابراین، اگر مجموعه (A۲) ناسازگار باشد آنگاه شمای صورت استدلالی (A۱) معتبر خواهد بود.
از (۱) و (۲) به دست میآید:
یک صورت استدلال معتبر است اگر و فقط اگر مجموعه صورتهای گزارهای مقدمات و نقیض نتیجه آن ناسازگار باشد.
پیش از توضیح روش درخت و کارزدن آنچه گفتیم، به معرفی ساختار درخت میپردازیم.
۱. ساختار درختی
در فصل دوم کتاب با ماتریس و کاربرد آن در حل مسائل فکری آشنا شدیم. ماتریس گونهای ساختار است که میتوان آن را دیداری کرد، آنگونه که روابط بین دادهها در خانههای آن آشکاری یابد. جدول ارزش که فراوان از آنها در فصلهای ۹ و ۱۰ کتاب سود جستیم مورد دیگری از کاربرد ماتریس بود. در منطق ساختار دیگری نیز به نام درخت هست که افزون در خود منطق در دانش کامپیوتر نیز بسیار پرکاربرد است. در ادامه نگاهی ابتدایی به درخت و واژگان آن خواهیم داشت تا آنچه اینجا بدان نیاز است فراهم شود.
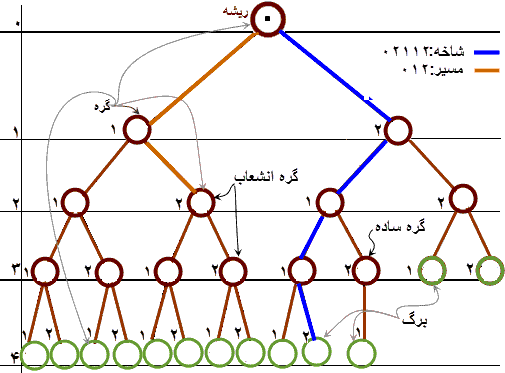
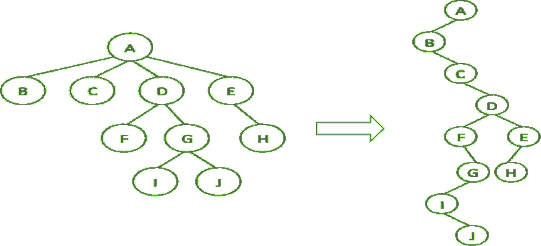
درخت:
یک درخت مجموعهای ساختیافته — مجموعهای که روابط تعریفشده بین اعضای آن وجود دارد — است.
گره:
اعضای درخت را گره مینامند. بجز گرهی که ریشه نام دارد، هر گره در درحت به فرض گره B توسط یک پیوند به یک و فقط یک گره به فرض گره A مرتبط است. دراینصورت، به A گره مقدمِ B [نیز مادر B] و به گره B تالی گره A [نیز فرزند B] میگوییم. بنابراین، هر گره در درخت (بهجز ریشه) دارای گره مقدم است. هر مادر میتواند هر تعداد فرزند داشته باشد. اما، هر درخت یک و فقط یک ریشه دارد. گرههای بیفرزند برگ (یا گره انتهایی) نام دارند.
یک گره تنها بهخودیخود یک درخت تک عضوی است. یک زیر درخت زیرمجموعهای از گرههای درخت است که خود یک درخت باشد. محتوی گرهها را فقره داده گره مینامند. درخت را میتوان ترازبندی درخت کرد و فرزندهای هر گره را از چپ به راست شمارهبندی کرد. به چنین درختی یک درخت مرتب میگوییم و در این صورت میتوان از فرزند اول، فرزند دوم، . . . یک گره و در صورت دودویی بودن درخت از فرزند چپ و فرزند راست سخن گفت.
مسیر:
یک مسیر در یک درخت یک دنباله شمارا است که عنصر اول آن ریشه درخت و هر عنصر بجز عنصر آخر دنباله (اگر وجود دارد) مادر عنصر بعدی دنباله باشد. بنابراین یک پیوند خود یک مسیر است.
شاخه:
یک شاخه در یک درخت مسیری است که عنصر آخر آن (در صورت محدود بودن مسیر) یک گره انتهایی (برگ) باشد.
گره ساده:
گره ساده گرهای است که دقیقاً یک فرزند داشته باشد. برای مثال، گره ۱۲ در درخت بالا یک گره ساده است. در این درخت فقط همین گره یک گره ساده است.
گره گسست:
گره گسست گرهای است که بیش از یک فرزند داشته باشد. برای مثال، گره ۹ و ۳ و مانند آنها در درخت بالا یک گره گسست هستند.
درخت دودویی:
درخت دودویی (درخت دودویی) درختی است که در آن هر مادر حداکثر دو فرزند داشته باشد.
۲. ساختن درخت صدق:
درخت صدق (نیز تابلویِ معنا یا درخت معنا یا روش تابلو) در اساس یک الگوریتم کارساز برای آزمون اعتبار استدلال است. خروجی این روند یک ساختار درختی است که در آن شرایط صدق پذیری استدلال مورد آزمون به نمایش درآمده. در این روند مقدمات و نقیض نتیجه استدلال بر اساس مجموعه معینی از قواعد به سادهترین مؤلفههای تشکیلدهنده آن در یک ساختار درختی کاهش مییابد. اگر همه شاخههای درخت بدستآمده دربردارنده تناقض (اصطلاحاً بسته) باشند آنگاه درخت نشاندهنده اعتبار استدلال دادهشده است. در غیر این صورت، یعنی اگر بعضی شاخههای درخت بدستآمده بسته نباشند آنگاه درخت نشاندهنده بیاعتباری استدلال است.
روند درخت صدق از ساختن ریشه آن آغاز و سپس شاخ و برگ آن طبق قواعد معین موسوم به قواعد درخت صدق ر,یانده میشود. همانطور که خواهیم دید، این روند کارآمد و بنابراین پایانپذیر و بعلاوه کارساز است. ما این روند را در اینجا با ارائه مثال و همراه با توضیح لازم معرفی میکنیم. این روند دارای دو گام است. در گام اول ریشه ایجاد میشود. گام دوم تکرار چرخههایی آنگونه است که در هر چرخه بخشی از درخت ساخته شود. تکرار چرخهها پایانپذیر است و سرانجام آن ساخت درخت کامل است بهقسمیکه، اعتبار یا بیاعتباری استدلال در آن نمایان است.
۳. قواعد ساخت درخت صدق:
جدول زیر که به قواعد ساخت درخت صدق موسوم است روش تحلیل (کاهش) هر فرمول در ساختن درخت صدق را نشان میدهد. در ادامه، با روش کارزدن آنها در آزمون اعتبار (و بیاعتباری) استدلال آشنا میشویم.
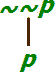 قاعده نفی دوگانه [پیوست ۱] | 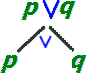 قاعده فصل [گسست ۲] | 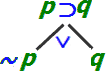 قاعده شرطی [گسست ۱] |
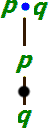 قاعده عطف [پیوست ۴] | 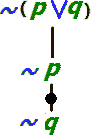 قاعده نفی فصل [پیوست ۳] | 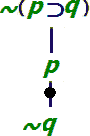 قاعده نفی شرطی [پیوست ۲] |
 قاعده نفی عطف [گسست ۵] | قاعده دو شرطی [گسست ۴] | قاعده نفی دو شرطی [گسست ۳] |
| جدول ۱. قواعد ساخت درخت صدق (معنا) | ||
مثال ۱:
میخواهیم اعتبار صورت استدلال زیر را بسنجیم:
(P۱): p ⊃ q
(P۲): r ∨ ~q
∴ (p ∨ q) ⊃ r
گام یکم: ایجاد ریشه درخت
در سیاهه بالا (یعنی، صورت استدلال دادهشده)، بجای نتیجه، نقیض آن را قرار میدهیم تا مجموعه زیر را داشته باشیم:
(۱) : Root = { p ⊃ q, r ∨ ~q, ~((p ∨ q) ⊃ r)}
گره ریشه را ایجاد و محتوای آن را مجموعه Root قرار میدهیم.
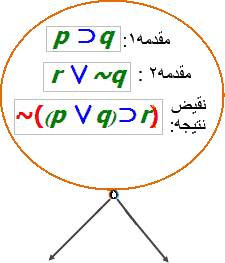
اگر نشان دهیم: محتوای ریشه، یعنی مقدمات صورت استدلال داده شد و نقیض نتیجه آن، دارای مدل نیست آنگاه: صورت دادهشده معتبر است (به عبارت دیگر، اگر نشان دهیم محتوای ریشه ناسازگار است آنگاه: صورت دادهشده معتبر است)؛
وگرنه صورت استدلال دادهشده نامعتبر است.
گام دوم: تکرار چرخههای کاهش برای گسترش درخت
این گام، تکرار چرخههای تحلیل فرمولها (یا عبارتهای گزارهای) دخیل در روند مطابق قواعد معین موسوم به قواعد ساخت درخت صدق، خواهد بود.
تکرار این چرخهها را مادام که یکی از شرایط زیر برقرار نیست ادامه میدهیم:
آ- درخت بسته است، یعنی گسترش بیشتر آن مستلزم تناقض است. در این حالت استدلال دادهشده معتبر است.
یا
ب- درخت باز است ولی هیچ شاخه آن قابل تحلیل (کاهش) بیشتر نیست. در این حالت استدلال دادهشده نامعتبر است.
اینک اولین چرخه:
(چرخه-۱)
یکی از صورتهای هنوز تحلیل نشده در گرههای درخت را برای تحلیل (یعنی کار زدن قواعد درخت روی آن) انتخاب میکنیم. این یک انتخاب دلخواه است و میتواند هر عنصر تحلیل نشده در درخت باشد. در اینجا صورت:
I: ~((p ∨q)⊃r)
را انتخاب میکنیم. [در ادامه توضیح خواهیم داد، گرچه این انتخاب دلخواه است و هر انتخابی (تحلیل نشده) ما را به سرمنزل مقصود میرساند، اما بسته به عنصر انتخابی میتوان زودتر یا دیرتر به سرمنزل رسید.]
شمای (I) همان شمای ریشهیِ قاعده نفی شرطی است. بنابراین، قاعده نفی شرطی را به (I) بکار میزنیم.
آنچه تا اینجا آمد را تحلیل فرمول~((p∨q)⊃r) بنا بر قواعد درخت صدق مینامیم و آن را بر درخت هنوز بسته نشده صدق، شکل ۱ در زیر، میرویانیم:
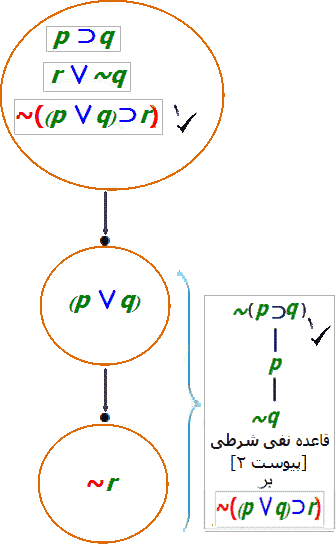
تحلیل فرمول ~((p∨q)⊃r) بنا بر قاعده قاعده نفی شرطی: نشانه تیک، ✔، در نمودار نشان میدهد که عبارت تیک خورده هماکنون تحلیلشده است. این درخت دارای سه گره است که محتوی ریشه آن مقدمات صورت استدلال و نقیض نتیجه آن است.
ازآنجاکه در درخت شکل ۱ هنوز فرمولهای تیک نخورده (تحلیل نشده) مانند r∨~q وجود دارد و درخت بسته نیست نیاز به چرخه دیگر برای تحلیل آن است. پس:
(چرخه-۲)
در چرخه ۲ صورت r∨~q (مقدمه دوم) از عناصر درخت را که هنوز تیک نخورده برای تحلیل انتخاب میکنیم. شمای این صورت همان شمای قاعده فصلی است. بنابراین، قاعده نفی شرطی را به r∨~q بکار میزنیم. حاصل آنچیزی است در شکل ۲ نمودار شده است.
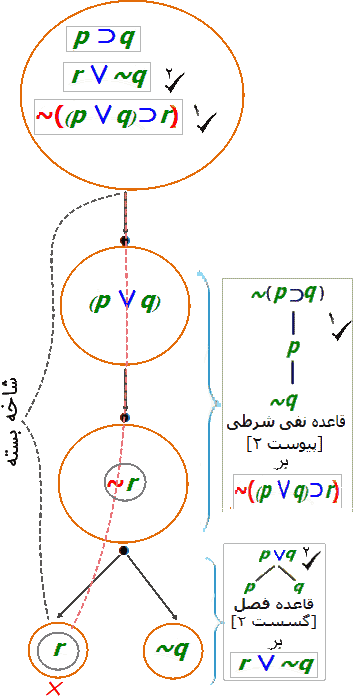
تحلیل فرمول: r∨~q. نشانه ×، در نمودار نشان میدهد در روند ساختن درخت، این شاخه بسته و گسترش آن پایانیافته، زیرا ادامه آن مستلزم تناقض است (تعبیری مدل r و نیز ~r است.)
ازآنجاکه در درخت شکل ۲ هنوز فرمولهای تیک نخورده (تحلیل نشده) مثل p⊃q و نیز شاخه باز وجود دارد نیاز به چرخه دیگر برای تحلیل آن است. پس:
(چرخه-۳)
در چرخه ۳ صورت p⊃q (مقدمه سوم) از عناصر درخت را که هنوز تیک نخورده برای تحلیل انتخاب میکنیم. شمای این صورت همان شمای قاعده شرطی است. بنابراین، قاعده شرطی را به p⊃q بکار میزنیم. حاصل آنچیزی است در شکل ۳ نمودار شده است.
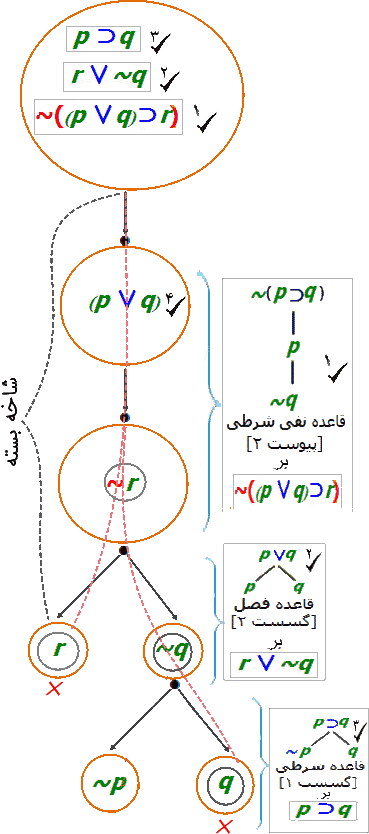
تحلیل p⊃q. نشانه ×، در نمودار نشان میدهد در روند ساختن درخت، این شاخه بسته شده و گسترش آن پایانیافته، زیرا مستلزم تناقض است (تعبیری مدل q و نیز ~q است.)
ازآنجاکه در درخت شکل ۳ هنوز فرمولهای تیک نخورده (تحلیل نشده) مثل p∨q وجود دارد نیاز به چرخه دیگر برای تحلیل آن است. پس:
(چرخه-۴)
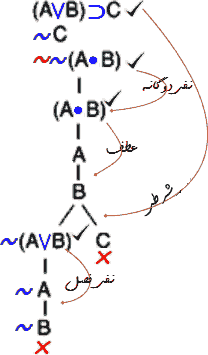
در چرخه ۴ صورت p∨q (مقدمه سوم) از عناصر درخت را که هنوز تیک نخورده برای تحلیل انتخاب میکنیم. شمای این صورت همان شمای قاعده فصلی است. بنابراین، قاعده فصلی را به p∨q بکار میزنیم. حاصل آنچیزی است در شکل ۴ نمودار شده است.
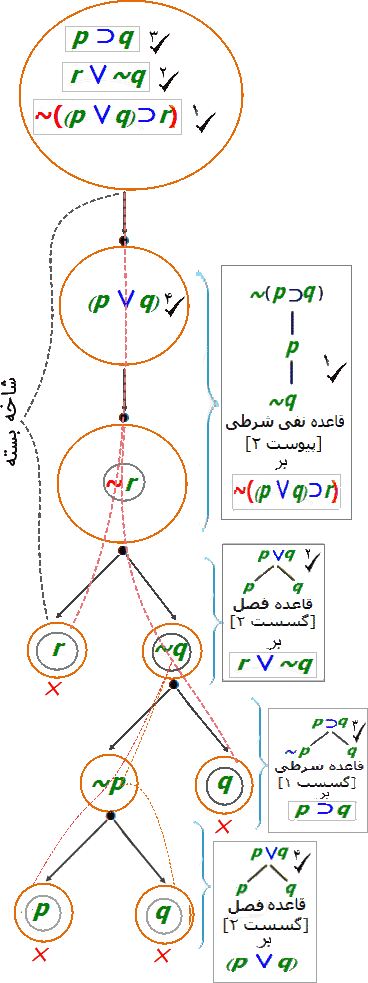
تحلیل p⊃q. نشانه ×، در نمودار نشان میدهد تمام برگهای درخت بستهاند (مسیر منهی به آنها بسته است. بعلاوه، فرمول قابلتحلیل دیگری که هنوز تحلیل نشده باشد در درخت وجود ندارد. بنابراین، همه تعبیرها برای مجموعه فرمول ('۱) منجر به تناقض میشود. و ازاینجا، میگوییم این مجموعه فرمول مدل ندارد. بنابراین، بنابر آنچه در بالا، زیر عنوان بنمایه روش درخت صدق گفته شد، صورت استدلال دادهشده معتبر است.
■ شاخه، درخت بسته و باز:
در یک درخت صدق شاخهای که شامل یک فرمول و نقیض آن است را شاخه بسته مینامیم. شاخهای که بسته نباشد را شاخه باز میگوییم. درختی که همه شاخههای آن بسته باشند را درخت بسته مینامیم. درختی که بعضی شاخههای آن باز باشند را درخت باز مینامیم.
یک درخت صدق که بعضی فرمولهای ریشه آن تحلیلشده را درخت گسترشیافته جزئی مینامیم.
یک درخت گسترشیافته جزئی که همه فرمولهای شاخههای باز آن تحلیلشده را درخت کامل میگوییم.
۴. درخت صدق و توتولوژی:
گیریم α فرمول؛ اگر بتوان نشان داد ~α مدل ندارد (صدقپذیر نیست) آنگاه α توتولوژی است (نتیجه ۱).
مثال ۴:
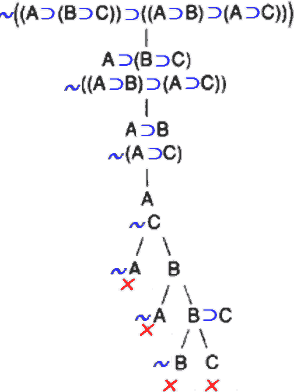
۵. ترتیب تحلیل فرمولها در درخت صدق:
درادامه (تمامیت درخت صدق)، خواهیمدید ترتیب تحلیل فرمولها در درخت صدق گرچه میتواند به درختهای ارزش متفاوت منجر شود ولی در نتیجه پایانی، یعنی معتبر بودن یا نامعتبر بودن استدلال، بیتأثیر است. در مثال زیر این نکته نشان دادهشده.
مثال ۶:
در این مثال با دو گسترش متفاوت درخت صدق، به قسمی که ترتیب تحلیل فرمولها در آنها متفاوت است، نشان میدهیم صورت استدلال زیر معتبر است:
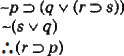
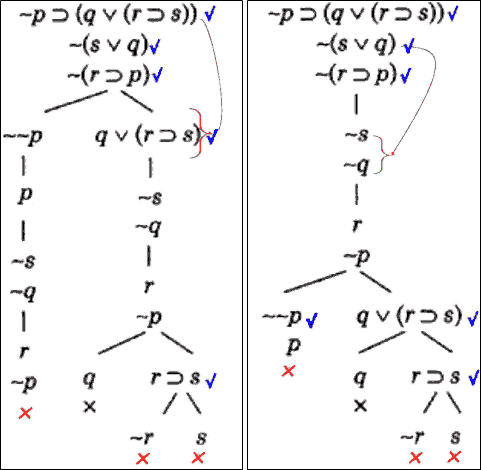
دو درخت صدق به دو ترتیب متفاوت در تحلیل فرمولها نشان میدهند صورت استدلال دادهشده معتبر است.
بهعنوان یک راهکار در گسترش درخت صدق میتوان ترتیب زیر را مدنظر داشت:
- قواعد نفی (نقیض) را بکار زد.
- قواعدی که منجر به گسترش خطی (غیر انشعابی) درخت میشوند را بکار زد.
۶. استواری تکنیک درخت صدق:
به قیاس همان روند که در طرح سردستی اثبات فرا-قضیه استواری برای دستگاه CND گفته شد، میتوان نشان داد تکنیک درخت صدق، به شمول قواعد آن، سرایت دهنده صدق منطقی است. بهعبارتدیگر، درخت صدق همچون یک نظریه مبتنی بر مدل (معنا شناختی / سمانتیک) استوار / متقن است. این ویژگی را استواری روش درخت صدق میگوییم.
اکنون میتوان نوشت:
| ⊢درخت صدق | ⇒ | ⊩جدول ارزش |
استواری درخت صدق را نیز میتوان با عبارت زیر بیان کرد:
هر صورت استدلال که درخت کامل بسته دارد یک صورت استدلال معتبر است.
۷. تمامیت تکنیک درخت صدق:
تمامیت روش درخت صدق وارون استواری درخت صدق است. این خاصیت را که اینجا اثبات آن را فرو میگذاریم بهقرار زیر مینویسیم:
| ⊩جدول ارزش | ⇒ | ⊢درخت صدق |
تمامیت روش درخت صدق را نیز میتوان با عبارت زیر بیان کرد:
هر صورت استدلال معتبر دارای درخت کامل بسته است.
۸. استواری و تمامیت تکنیک درخت صدق:
با توجه به استواری درخت صدق و تمامیت درخت صدق میتوان نوشت:
| ⊢درخت صدق | ⇔ | ⊩جدول ارزش |
بنابراین میتوان گفت:
۹. تصمیم پذیری:
مسئله تصمیم پذیری درخت صدق، با توجه آنچه در مورد روند ساخت درخت صدق گفته شد، به پایانپذیری آن برمیگردد. میتوان دید که کارزدن قواعد ساخت درخت صدق به هر فرمول به کاهش طول فرمول، یعنی تعداد نمادهای آن، میانجامد. بنابراین، بهطور شهودی میتوان گفت حداکثر پس از کار زدن تعداد محدود قواعد درخت صدق به برگی خواهیم رسید که قابلتحلیل بیشتر نباشد. بهعبارتدیگر، روند درخت صدق در تعداد محدود از چرخههای تحلیل به درخت کامل منتهی خواهد شد.
آ. معرفی وبگاه برای حساب درخت صدق:
با جستجو در وب میتوان وبگاههایی را برای محاسبه درخت صدق (نیز تکنیکهای دیگر) یافت. در زیر آدرس یک وبگاه، که صرفاً با جستجوی ساده یافته، برای آشنایی آمده:
http://umsu.de/logik/trees/ Tree Proof Generator.
ب. معرفی برخی کتاب:
| دو کتاب زیر رهیافت درخت را بکار بردهاند. |
 An Introduction to Symbolic Logic در فصل ۴ این کتاب اثبات استواری و تمامیت تکنیک درخت صدق را میتوان یافت. |
 چاپ سوم این کتاب(۱۹۶۷) به شرح زیر به فارسی ترجمه و نشر گردیده است. ویرایش جدید، متن اصلی، این کتاب (۲۰۰۶) دارای دو تکمیلی افزوده است. قلمرو و مرزهای منطق صوری؛ تالیف ریچارد جفری؛ ترجمه پرویز پیر تهران؛ علمی و فرهنگی، ۱۳۶۶. |