منطق محمولات: زبان، تعبیر و مدل (۱)

منطق و فرامنطق

درآمد به منطق

منطق محمولات: زبان، تعبیر و مدل (۱)

۱- مقدمه	۷- قلمرو سور
۲- منطق محمولات، تعبیر و معنا	۸- رویدادهای پابند و آزاد متغیرها
۳- عناصرزبان منطق مرتبه اول	۹- فهرست متغیرها
۴- ترم (Term) درزبان محمولات	۱۰- آزادی ترم (عبارت اسمی) برای متغیرها
۵- فرمول خوش-ساخت	۱۱- زبان، تعبیر و صدق
۶- پرانتزها در فرمول‌ها	۱۲- مثال‌ها: فرمول و تعبیر

توجه: مگر در مواردی که با نماد "" مشخص شده باشد، محتوای ارائه شده در این یادداشت از مرجع زیر برگرفته و برگردان شده است.

Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. p. 45-60.

■ مقدمه

در این یادداشت و یادداشت بعد، با تمرکز بر نقش محوری تعبیر (رویکرد مبتنی بر مدل ↝↝) در درک و به کارگیری این جنبه بنیادی از منطق، به دنیای پیچیده منطق محمولات می‌پردازیم. منطق محمولات که به عنوان منطق مرتبه اول نیز شناخته می‌شود، با معرفی سورها و متغیرهایی که امکان بیان گزاره‌های پیچیده‌تر در مورد اشیا و روابط آنها را فراهم می‌کند، فراتر از قلمرو منطق گزاره‌ای گسترش می‌یابد. در قلب این کاوش، انگاشت تعبیر قرار دارد، که به عنوان پیوندی بین نمادهای انتزاعی زبان منطقی ما و معانی آنها در زمینه‌های خاص عمل می‌کند. این یادداشت (و یادداشت بعد)، که به چهار بخش اصلی تقسیم شده است، به گونه‌ای تدوین یافته که ما را در این چشم انداز پیچیده به شیوه‌ای روشمند پیش ببرد. این ۴ بخش به قرار زیر هستند که دو بخش اول در این یادداشت و دو بخش بعدی در یادداشت پس از این آمده است.

۱. منطق محمولات، تعبیر و معنا،
۲. عناصر زبانی منطق مرتبه اول،
۳. زبان، تعبیر و صدق
۴. صدق، صدق‌پذیری، و مدل

بخش اول، «منطق محمولات، تعبیر و معنا» با معرفی منطق محمولات و نقش تعیین کننده‌ای که تعبیر در معنا بخشیدن به نمادها و فرمول‌های درون این منطق دارد، صحنه را برای ورود آماده می‌کند. ما بررسی خواهیم کرد که چگونه تعبیرهای گوناگون می‌توانند به نتایج متفاوتی در مورد عبارات منطقی یکسان منجر شوند، که این اهمیت زمینه را در درک منطق محمولات برجسته می‌کند.

در «عناصر زبانی منطق مرتبه اول»، تمرکز خود را به بلوک‌های سازنده منطق مرتبه اول تغییر می‌دهیم. این بخش نحو زبان، از جمله نمادها، فرمول‌ها و قواعد ساخت فرمول خوش-ساخت را پوشش می‌دهد. درک این عناصر برای هر کس که به دنبال آسودگی در منطق محمولات، علوم کامپیوتر و فلسفه باشد، ضروری است، زیرا آنها پایه‌ای را تشکیل می‌دهند که تعابیر بر آن پایه‌ها بنیاد می‌شوند.

بخش سوم (یادداشت بعد)، «زبان، تعبیر و صدق»، عمیق‌تر به رابطه بین زبان و تعبیر آن می‌پردازد. با تأکید بر مفاهیم ارزش‌های صدق (حقیقت -Truth)، صدق پذیری (Satisfaction)، و شرایطی که تحت آن یک گزاره در یک تعبیر معین درست یا نادرست در نظر گرفته می‌شود بررسی خواهیم کرد که چگونه درستی گزاره‌ها در منطق مرتبه اول با تعبیر آنها تعیین می‌شود.

سرانجام، «صدق، صدق‌پذیری و مدل» مفاهیم صدق و صدق‌پذیری را در چارچوب مدل‌ها بررسی می‌کند - تعبیری که همه گزاره‌های یک نظریه را برآورده می‌کند. در این بخش مفهوم مدل، نقش آنها در تعیین صدق گزاره‌های معرفی می‌شود.

در پایان امید است، درک جامعی از منطق محمولات و نقش اصلی تعبیر و مدل در پیوند جهان انتزاعی فرمول‌های منطقی با واقعیت‌های انضمامی که آنها قصد توصیف آن را دارند، داشته باشیم. افزون بر این، این کاوش می‌کوشد تا ابزارهایی را معرفی کند تا بتوان با کارآمدی بیشتر با کارزدن آنها درگیر شد.

■ منطق محمولات، تعبیر و معنا

در قسمت ششم↝ (منطق محمولات↝) از فصل یازدهم «کتاب درآمد به منطق↝» به انگاشته‌های جهان ممكن، تعبیر و مدل پرداخته شده است. فرآیند توصیف شده در آن فصل برای تعبیر شامل جایگزینی ثابت‌های منفرد برای متغیرهای منفرد در یک جهان معین است. از این روش تعبیر به عنوان تعبیر جایگزینی↧ (Substitutional Interpretation) یاد می‌شود. از پیشگامان این روش می‌توان به منطق دانانی مانند لشنیوسکی↝ و تارسکی↝ اشاره کرد. رویکرد دیگری برای تعبیر زبان محمولات که در اینجا مورد توجه خواهد بود، به عنوان تعبیر عینی (Objective Interpretation) شناخته می‌شود. این رویکرد به معیار در زمینه‌هایی مانند منطق، ریاضیات و علوم کامپیوتر تبدیل شده است. این روش مبتنی بر نظریه صدق↧ است که توسط آلفرد تارسکی↝، یکی از تأثیرگذارترین منطق‌دانان قرن بیستم، توسعه یافته است.

• Dunn, J. Michael, and Nuel D. Belnap. The Substitution Interpretation of the Quantifiers. Noûs 2, no. 2 (1968): 177–85.

• James W. Garson. The substitution interpretation and the expressive power of intensional logics., Notre Dame Journal of Formal Logic Volume XX, Number 4, October 1979.

⦁ Tarski, A. (1935). Der Wahrheitsbegriff in den formalisierten Sprachen. Studia Philosophica, 1, 261–405.

⦁ Logic, Semantics, Metamathematics, Papers from 1923 to 1938, by Alfred Tarski, Translated by J. H. Woodger. Oxford at the clarendon press, 1956 (p. 152 - 278).

یادآور می‌شود که در فصل یازدهم (منطق محمولات↝ - درآمد به منطق↝) منطق گزاره‌ها به منطق محمولات گسترانده شد. در زبان این دستگاه افزون بر عناصر زبان گزاره‌ای، این عناصر — یعنی متغیرهای انفرادی (فقط متغیر 'x')، ثابت‌های انفرادی، حروف محمولی، سور عمومی و سور وجودی — وجود دارند. وجود تنها یک متغیر 'x' و حروف محمولی یک جایبانی، مدل‌سازی برخی گزاره‌های (در نتیجه بعضی استدلال‌های) زبان طبیعی در این زبان را پیچیده می‌کند. برای مثال گزاره «همه انسان‌ها آب می‌نوشند.» را در نظر بگیرید. اگر بخواهیم این گزاره را به یک گزاره حملی استاندارد-ساخت [↝-↝] برگردانیم باید بنویسیم:

«همه انسان‌ها موجوداتی که آب می‌نوشند هستند»

یا کوتاهتر «همه انسان‌ها آب-نوش هستند».

در این صورت می‌توان نوشت: (x)(Hx⊃Ax) که در آن H و A به ترتیب حروف محمولی برای «انسان-بودن» و «آب‌نوش-بودن» است. در اینجا ما در ازای ایجاد انگاشت «آب-نوش» دو انگاشت «آب» و «نوشیدن» را از دست داده‌ایم. این ساده‌سازی نشان می‌دهد که چگونه فرآیند انتزاع در یک زبان یک متغیری گاهی اوقات می‌تواند عناصر متمایز را در یک انگاشت واحد ادغام کند و به طور بالقوه برخی از تفاوت‌های گزاره اصلی را از دست بدهد. یا در گزاره‌ جزئی «شهری وجود دارد که از شهر دیگر بزرگتر است — بعضی شهرها از شهرهای دیگری بزرگتر هستند» مساله پیچیده‌تر نیز می‌شود. [برای توضیح بیشتر مقوله «نسبی» (Things toward something - Relative) در دانشنامه فلسفه استنفورد را در اینجا ببینید.]

در زیر به عنوان نمونه دو استدلال معتبر در زبان طبیعی آمده و سپس برگردان آنها به زبان محمولات با بیش از یک متغیر نشان داده است↧.

Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. p. 45.

۱-
هر که دوست پرویز است دوست جاوید هم است.
مهرداد دوست جاوید نیست.
———————————————
پس مهرداد دوست پرویز نیست.

در این استدلال حرف محمولی دو جایبانی F(_, _) را برای دوست داشتن می‌گیریم. پرویز، جاوید و مهرداد را با به ترتیب ثابت‌های انفرادی j ،p و m نشان می‌دهیم. در این صورت داریم:

(∀x)(F(x, p) ⇒ F(x, j))
¬F(m, j)

——————

¬F(m, p)

۲-
همه انسان‌ها عقلانی است.
بعضی حیوان‌ها انسان هستند.
———————————————
بتابراین، بعصی حیوان‌ها عقلانی هستند.

در این استدلال R ،H و A را به ترتیب برای انسان بودن، عقلانی بودن و حیوان بودن در نظر می‌گیریم. در این صورت داریم:

(∀x)(H(x) ⇒ R(x))
(∃x)(A(x) ∧ H(x))
——————————
(∃x)(A(x) ∧ R(x))

صحت این دو استنباط نه تنها بر معنی رابط‌های تابع-ارزش، بلکه بر معنای سورها ↝ (کمیت‌سازهای «همه / هر»↝ و «برخی»↝) و دیگر ساخت‌های زبانی استوار است.

■ عناصر زبان منطق مرتبه اول (Language of First-Order Logic)

زبان منطق مرتبه اول (کوتاه شده به صورت fol) شامل اجزای زیر است↧:

Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. p. 47.

۰- نمادهای «,»، «)»، «(»، نیز رابط‌های‌ «¬» و «⇒» در زبان 𝓛 (حساب گزاره‌ای).

۱- سور عمومی ↝ به عنوان رابط‌ منطقی (نماد سور عمومی را '∀' می‌گیریم.)

۲- متغیرهای انفرادی عبارتند از:

x_۱, x_۲, . . . ,x_n, . . .

۳- ثابت‌های انفرادی عبارتند از:

a_۱, a_۲, . . . ,a_n, . . .

۴- حروف محمولی عبارتند از `A_k^n`:

که در آن n (برای مشخص کننده تعداد جایبان حرف محمولی) و k (برای اندیس حرف محمولی) می‌توانند هر عدد صحیح مثبت باشند.

۵- حروف تابعی عبارتند از `f_k^n`:

که در آن n (برای مشخص کننده تعداد جایبان حرف تابعی) و k (برای اندیس حرف محمولی) می‌توانند هر عدد صحیح مثبت باشند.

■ ترم (Term) در زبان محمولات

انگاشت ترم در fol‍ را به شیوه بازگشتی↝ ↝ مطابق زیر تعریف می‌کنیم.

۱- متغیرهای انفرادی `x_۱,x_۲,...,x_n,...` و ثابت‌های انفرادی `a_۱,a_۲,...,` ترم هستند.

۲- اگر `f_k^n` یک حرف تابعی باشد و `t_۱, t_۲, . . .,t_n` ترم باشند آنگاه `f_k^n(t_۱, t_۲, . . .,t_n)` نیز یک ترم است.

۳- یک عبارت یک ترم است اگر و تنها اگر بتوان نشان داد که بر مبنای شرط‌های ۱ و ۲ به دست آمده است.

ترم‌ها با آنچه در زبان‌های طبیعی نام‌ و عبارت‌های اسمی↝ نامیده می‌شوند — برای مثال، «دو»، «دو به علاوه سه» و «دو به علاوه x» — مطابقت دارند . با کار زدن حرف محمولی روی ترم‌ها یک فرمول اتمی به دست می‌آید. برای مثال اگر حرف محمولی `A_k^۲` را روی `t_۱` و `t_۲` اعمال کنیم فرمول اتمی `A_k^۲(t_۱, t_۲)` به دست خواهد آمد.

توجه: با استفاده از حروف تابعی و تعبیر آنها به عنوان تابع در دامنه بحث می‌توان از ترکیب اشیای منفرد دامنه، در مورد اشیای جدیدی که از این ترکیب‌ها حاصل می‌شوند صحبت کرد. حروف تابعی زبان محمولات را توانا می‌سازد تا گستره وسیع‌تری از معانی و روابط را نسبت به آنچه که فقط با حروف محمولی و ثابت‌های انفرادی امکان‌پذیر است، گسترش دهد و به توان بیانی زبان بیافزاید. بدون حروف تابعی، زبان محمولات بطور قابل توجهی در توانایی خود چه برای نشان دادن و چه برای استدلال در مورد انواع روابط و ویژگی‌های ترکیبی که در زبان طبیعی و در دستگاه‌های صوری رایج است، محدود می‌شود. برای مثال، به استدلال زیر در زبان فارسی توجه کنید:

۳-

تالی بیواسطه ↝ یک عدد صحیح زوج فرد است.
۲ عدد صحیح زوج است.
————————————
بنابراین، تالی بیواسطه ۲ فرد است.

برگردان این استدلال به زبان محمولات عبارت است از:

(∀x)(I(x) ∧ E(x) ⇒ D(ƒ(x))).
I(b) ∧ E(b)
——————
D(ƒ(b))

که در آن E، I و D را به ترتیب مشخص کننده ویژگی‌های عدد صحیح بودن، عدد زوج بودن و عدد فرد بودن هستند. ƒ(x) (ƒ به عنوان حرف تابعی) معین کننده تالی بی‌واسطه x و b نشان دهنده عدد صحیح ۲ است.

■ فرمول خوش-ساخت (Well-formed formula)

فرمول خوش-ساخت (wff) در fol مطابق زیر تعریف می‌شود:

۱- هر فرمول اتمی یک wff است.

۲- اگر β و ς هر دو wff و x و y متغیر باشند آنگاه:

`(¬β), (β ⇒ ς)` و `((∀x)β)`

هر دو wff هستند.

۳- یک عبارت یک wff است اگر و تنها اگر بتوان نشان داد که بر مبنای شرط‌های ۱ و ۲ به دست آمده است.

• سور وجودی↝ را نه به عنوان یک انگاشت ابتدایی بلکه `((∃x)β)` را به عنوان کوتاه شده:

`(¬((∀x)(¬β)))` ↜

در نظر می‌گیریم. که در آن β یک فرمول خوش-ساخت است.

• عبارت‌های:

`(β ⇔ ς) - (β ∨ ς) - (β ∧ ς)`

در اینجا همانطور که در دستگاه `ℒ` تعریف شده است↝ تعریف می‌شوند.

برای آسان‌تر کردن خوانش فرمول‌ها، از u، v، x، y، z برای متغیرهای انفرادی، از A، B، C برای حروف محمولی، از f، g، h برای حروف تابعی و از a، b، c برای ثابت‌های انفرادی استفاده خواهیم کرد.

■ پرانتزها در فرمول‌ها

همان قراردادهایی که در رده‌بندی تقدمی رابط‌ها در مورد حذف پرانتزها ایجاد شد، در اینجا هم برقرار است. با این قرارداد اضافی که سور‌های (∀x) و (∃x) از نظر سطح رده‌بندی بین ¬، ∧، ∨ و ⇒، ⇔ قرار می‌گیرند. به عبارت دیگر، در بازگذاری پرانتزها، ابتدا به نقیض، عطف و فصل، سپس به سور‌های عمومی و وجودی و بعد از آن به شرطی‌ها و دو شرطی‌ها می‌پردازیم. مانند قبل، برای رابط‌های از یک نوع، از چپ به راست پیش می‌رویم. برای نقیض‌ها و سور گزاری‌های متوالی، از راست به چپ پیش می‌رویم. در مثال‌های زیر بازگذاری پرانتزها نشان داده است.

مثال برای بازگذاری پرانتز‌ها

۱- `(∀x_۱)A_۱^۱(x_۱)⇒A_۱^۱(x_۲, x_۱)`
`((∀x_۱)A_۱^۱(x_۱))⇒A_۱^۱(x_۲, x_۱)`
`(((∀x_۱)A_۱^۱(x_۱))⇒A_۱^۱(x_۲, x_۱))`

۲- `(∀x_۱)A_۱^۱(x_۱)∨A_۱^۱(x_۲, x_۱)`
`(∀x_۱)(A_۱^۱(x_۱)∨A_۱^۱(x_۲, x_۱))`
`((∀x_۱)A_۱^۱(x_۱))∨A_۱^۱(x_۲, x_۱)))`

۳- `(∀x_۱)¬(∃x_۲)A_۱^۲(x_۱, x_۲)`
`(∀x_۱)¬((∃x_۲)A_۱^۲(x_۱, x_۲))`
`(∀x_۱)(¬((∃x_۲)A_۱^۲(x_۱, x_۲)))`
`((∀x_۱)(¬((∃x_۲)A_۱^۲(x_۱, x_۲))))`

■ قلمرو سور

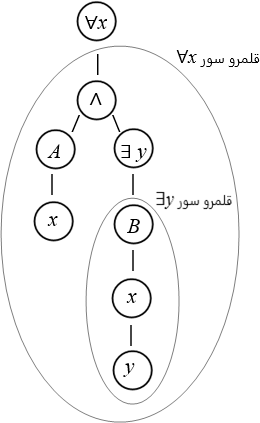
فرض کنید ((Qx)β) یک wff، که در آن Q نماد سور است، باشد. در این صورت `β` قلمرو سور '(Qx)' نامیده می‌شود.

برای مثال در فرمول:

`(∀x)(A(x)∧(∃y)B(x,y))`

فرمول:

`obrace(A(x)∧(∃y)B(x,y))`،

در قلمرو سور `∀x` است.

(به یاد داشته باشید که `(EEx_j)` کوتاه شده `¬(AAx_1)¬` است).

(نیز توجه داشته باشید که β نیازی به متغییر y ندارد. در این صورت، ما ((∀y)β) را همان طور می‌فهمیم که β را می‌فهمیم).

■ رویدادهای پابند و آزاد متغیرها

به یک رویداد متغیر x در یک فرمول، به فرض β، رویداد پابند گفته می‌شود اگر:

آن رویداد x در سور (Qx) — (که در آن Q ∀ یا ∃ است) رخ داده باشد،

یا در قلمرو سور (Qx) در β رخ داده باشد. در این صورت به این رویداد متغیر یک رویداد آزاد در β گفته می‌شود.

مثال: رویدادهای آزاد و پابند

(۱). `A_۱^۲(x_۱,x_۲)`

متغیر `x_۱` در (۱) فقط یک بار روی داده است که در این رویداد زاد است.

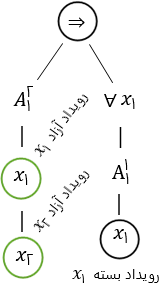(۲). `A_۱^۲(x_۱,x_۲)⇒(∀x_۱)A_۱^۱(x_۱)`

در (۲) رویداد `x_۱` در `A_۱^۲(x_۱,x_۲)` آزاد است، اما رویدادهای دوم و سوم آن پابند هستند.

(۳). `(EEx_1)A_۱^۲(x_۱,x_۲)`

در (۳) هردو رویداد `x_۱` پابند است.

[`(EEx_1)A_۱^۲(x_۱,x_۲)` کوتاه شده `¬(AAx_1)¬A_۱^۲(x_۱,x_۲)` است].

(۴). `(∀x_۱)A_۱^۱(x_۱)∧(∃x_۲)A_۱^۲(x_۱, x_۲)`

در این فرمول `x_۱` در دو رویداد اول خود پابند و در رویداد سوم آزاد است و `x_۲` در هر دو رویداد خود پابند است.

همانطور که در مثال (۲) و (۴) می‌توان دید یک متغیر می‌تواند در یک فرمول یکسان دارای رویداد پابند و هم رویداد آزاد داشته باشد.

■ متغیر آزاد

به یک متغیر در یک فرمول متغیر آزاد در آن فرمول می‌گویند اگر در آن فرمول دارای رویداد آزاد داشته باشد. به یک متغیر در یک فرمول متغیر پابند در آن فرمول می‌گویند اگر در آن فرمول دارای رویداد پابند داشته باشد. بنابراین، یک متغیر در یک فرمول یکسان می‌تواند هم آزاد و هم پابند باشد.

■ فهرست متغیرها

ما بیشتر وقت‌ها با نوشتن یک فرمول، به فرض `β`، به صورت `β(x_(i_1), . . . ,x_(i_k))` می‌خواهیم نشان دهیم که برخی از متغیرهای `x_(i_1), . . .,x_(i_k)`، متغیرهای آزاد در `β` هستند. این بدان معنا نیست که `β` شامل (همه) این متغیرها به عنوان متغیرهای آزاد است و همچنین به این معنی نیست که `β` شامل متغیرهای آزاد دیگری نیست. این نماد گذاری باعث آسانی می‌شود زیرا می‌توانیم قرارداد کنیم تا نتیجه جایگزین کردن ترم‌های `t_۱, .. . ,t_k` در `β` را به ترتیب بجای تمام رویدادهای آزاد `x_(i_1), .. .,x_(i_k)` (در صورت وجود) به‌ صورت `β(t_۱, ... ,t_k)` بنویسیم.

■ آزادی ترم (عبارت اسمی) برای متغیرها

آزادی ترم برای متغیر: فرض کنید β یک wfs و t یک ترم باشد. در این صورت گفته می‌شود که t برای متغیر x در β آزاد است [یا t متغیر x را در β نسبت به خود پابند نمی‌کند] اگر هیچ رویداد آزاد x در β در قلمرو هیچ سور y که در آن y متغیر t است نباشد.

مثال:

۱- ترم `x_۲` [یعنی،`t=x_۲`] برای متغیر `x_۱` در فرمول `A_۱^۱(x_۱)` آزاد است، زیرا هیچ رویداد آزاد متغیر `x_۱` در قلمرو هیچ سور از متغیرهای ترم `x_۲` نیست.

۲- ترم `x_۲` برای متغیر `x_۱` در فرمول `(∀x_۲)A_۱^۱(x_۱)` آزاد نیست، زیرا یک رویداد آزاد `x_۱` در قلمرو سور `x_۲` است.

۳- ترم `f_۱^۲(x_۱, x_۳)` برای متغیر `x_۱` در فرمول `(∀x_۲)A_۱^۲(x_۱, x_۲)⇒A_۱^۱(x_۱)` آزاد است، اما برای `x_۱` در `(∃x_۳)(∀x_۲)A_۱^۲(x_۱, x_۲)⇒A_۱^۱(x_۱)` آزاد نیست.

۱- یک ترم که دارای متغیر نباشد برای هر متغیر در هر فرمول آزاد است.

۲- ترم t برای هر متغیر در فرمول `β` آزاد است اگر هیچ یک از متغیرهای t در `β` متغیر پابند نباشند.

۳- ترم `x_i` برای `x_i` در هر فرمول آزاد است.

۴- هر ترمی برای `x_i` در فرمول `β` آزاد است اگر `β` دارای هیچ رویداد آزاد `x_i` نباشد.

توجه: انگاشت " آزادی ترم برای متغیر" در منطق مرتبه اول برای درک و به کارگیری صحیح سورها در عبارت‌های منطقی بسیار مهم است. این کمک می‌کند تا از ابهامات و تناقض‌هایی که هنگام جایگزینی ترم‌ها به عبارت‌های بوجود می‌آیند، به ویژه در حضور سورها، ایجاد شود. این انگاشت تضمین می‌کند که ساختار منطقی و معنای مورد نظر عبارات در طول جایگزینی حفظ می‌شود.

در fol‍‍، سورها متغیرها را به قلمرو خود پابند می‌کنند و بر تعبیر این متغیرها تأثیر می‌گذارند. هنگام جایگزین کردن یک عبارت برای یک متغیر در یک عبارت منطقی، ضروری است که اطمینان حاصل شود که جایگزینی به طور سهوی معنای عبارت را تغییر نمی‌دهد. یک ترم در یک فرمول "آزاد برای یک متغیر" است، اگر جایگزینی متغیر با آن ترم، متغیری را معرفی نکند که توسط یک سور پابند شده است، که می‌تواند ساختار منطقی یا تعبیر مورد نظر فرمول را تغییر دهد.

مثال ۱: فرمول `∀x (P(x) ⇒ Q(y))` را در نظر بگیرید و فرض کنید می‌خواهیم ترم `t` (به قرار `t = y`) را جایگزین `x` کنیم و این در حالی است که ترم `t` برای متغیر `x` آزاد نیست (رویداد آزاد `x` در قلمرو سور `y` در فرمول قرار دارد). این فرمول می‌گوید "برای هر `x` اگر`P(x)` برقرار باشد آنگاه `Q(y)` برقرار است، که در آن جایی `y` توسط سوری پابند نشده است و می‌توان آن را در زمینه این فرمول یک متغیر آزاد در نظر گرفت. اکنون، بدون در نظر گرفتن آزادی ترم `t` برای متغیر `x`، جایگزینی را انجام دهیم. پس از جایگزینی `y` به جای `x` خواهیم داشت:

`(∀y)(P(y) ⇒ Q(y)).`

این جایگزینی معنای فرمول را تغییر می‌دهد. در ابتدا، `y` آزاد بود و می‌توانست هر شیئ باشد که تحت تأثیر قلمرو سور قرار نمی‌گرفت. پس از جایگزینی، `y` توسط سور پابند می‌شود، و این فرمول اکنون به عنوان «برای هر `y` اگر `(P(y))` برقرار است آنگاه `(Q(y))` برقرار است» خوانده می‌شود که ادعایی متفاوت از ادعای اصلی است.

■ زبان، تعبیر و صدق

زبان‌های مرتبه اول که به عنوان حساب محمولات مرتبه اول یا منطق مرتبه اول نیز شناخته می‌شوند، به عنوان یک چارچوب توانمند برای صوری کردن گزاره‌ها و استدلال در ریاضیات، علوم کامپیوتر و منطق فلسفی (کار زدن منطق و دستگاه‌های صوری در مسائل فلسفی) عمل می‌کنند. این زبان‌ها منطق گزاره‌ای را با ترکیب سورها (کمی‌سازها) و متغیرها گسترش می‌دهند تا بتوانند به اشیاء در یک جهان سخن (گفتمان) اشاره کنند. نحو زبان‌های مرتبه اول شامل پیوندهای منطقی، سورها، متغیرها، نمادهای محمول، نمادهای تابعی و ثابت‌ها است. سمانتیک (معنا‌شناسی) یا معنای این زبان‌ها با تعبیرهای آنها به دست می‌آید.

■ تعبیر

یک تعبیر (روند تعبیری) برای یک زبان مرتبه اول عبارت است از مشخص کردن مجموعه‌ای ناتهی از اشیاء به عنوان حوزه گفتمانی (عالم سخن) آنگونه که متغیرها و ثابت‌های زبان به آنها اشاره کنند و انتساب معنی به عناصر این زبان را، به شرحی که در زیر آمده، سرانجام دهد:

۱- دامنه سخن (Domain of Discourse):

دامنه سخن عبارت از مجموعه‌ای است که گستره متغیرها است. این مجموعه می‌تواند هر مجموعه ناتهی، مانند مجموعه اعداد طبیعی، مجموعه افراد یک شهر و مانند آنها باشد.

۲- ثابت‌های انفرادی:

هر نماد ثابت‌ انفرادی به عنوان یک عنصر خاص از دامنه سخن تعبیر می‌شود.

۳- حروف محمولی:

هر حرف محمولی (n-جایبانی) به عنوان یک رابطه n-تایی در دامنه سخن تعبیر می‌شود. برای مثال، یک حرف محمولی (۲-گانه) می‌تواند با رابطه‌ای مانند "بزرگتر از" در مجموعه اعداد تعبیر شود.

۴- حروف تابعی:

هر حروف تابعی (n-جایبانی) به عنوان یک تابع n-متغیری در دامنه سخن تعبیر می‌شود. برای مثال، یک حرف تابعی (۲-جایبانی) می‌تواند با تابع دو متغیری جمع در مجموعه اعداد تعبیر شود.

■ صدق و صدیق‌پذیری (Truth and Satisfiability)

یک فرمول در یک زبان مرتبه اول صدق‌پذیر است اگر تعبیری باشد که این فرمول را برآورد (تحت آن تعبیر این فرمول دارای مقدار ارزش درست باشد). انگاشت صدق در منطق مرتبه اول نسبت به یک تعبیر تعریف می‌شود. یک عبارت گزاره‌ای (فرمولی بدون متغیرهای آزاد) در صورتی در تعبیر درست (صادق) است که رابطه بین اعضای دامنه سخن را دقیقاً، آنگونه که توسط تعبیر حروف محمولی و تابعی مشخص شده است، توصیف کند.

مدل:

یک مدل از مجموعه‌ای از جملات (عبارت‌های گزاره‌ای) در یک زبان مرتبه اول، تعبیری است که در آن تمام جملات درست باشند. بررسی مدل‌ها (نظریه مدل) به درک ویژگی‌های دستگاه‌های صوری و نظریه‌های پیکربندی‌شده در آنها می‌انجامد. یک نظریه سازگار است اگر دارای مدل باشد. یک نظریه تمام است اگر هر جمله (گزاره) یا نقیض آن در زبان قابل اثبات (دارای برهان) باشد.

■ مثال‌ها: فرمول و تعبیر

در این بخش، نمونه‌هایی از منطق جمله‌های محمولات را ارائه و به طور شهودی برخی تعبیر آنها را بررسی می‌کنیم. در بخش بعدی، ما به بحثی جامع در مورد تعبیر زبان‌های مرتبه اول خواهیم پرداخت و موضوع را با جزئیات پی خواهیم گرفت.

	فرمول	تعبیر
۱.	`(∃x_۱)A_۱^۱(x_۱)` اگر دامنه سخن را مجموعه انسان‌ها و `A_۱^۱(x_۱)` را انسان بودن بگیریم، آنگاه تعبیر فرمول جمله «انسان وجود دارد.» خواهد بود. همه رویدادهای `x_۱`دراین فررمول پایند است.
۲.	`(∃x_۱)(∀x_۲)(A_۱^۲(x_۱, x_۲))` اگر دامنه سخن را اعداد طبیعی مثبت بگیریم. `A_۱^۲(x_۱,x_۲)` را `x_۱≤x_۲` تعبیر ‌کنیم، آنگاه تعبیر این فرمول گزاره «عدد x_۱ وجود دارد که کوچکتر یا مساوی از هر عدد طبیعی مثبت است.» خواهد بود و از آنجا که فرمول در این تعبیر صدق پذیر (Satisfiable) است (برای عدد ۱) و چون سور این متغیر وجودی است پس این فرمول تحت این تعبیر درست است.
۳.	‍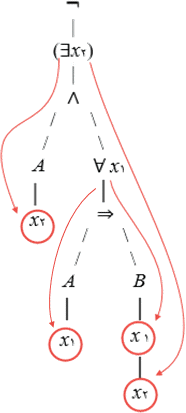`¬(∃x_۲)(A(x_۲)∧(∀x_۱)(A(x_۱)` `‍⇒` `B(x_۱, x_۲)))‍‍` اگر دامنه سخن را اعداد طبیعی بگیریم. A(x_۱) را x_۱ عدد طبیعی است تعبیر کنیم. B(x_۱,x_۲) را x_۱≤x_۲ تعبیر ‌کنیم. آنگاه تعبیر فرمول گزاره «بزرگترین عدد طبیعی وجود ندارد.» خواهد بود و چون سور x_۱ عمومی است پس این فرمول تحت این تعبیر درست است.
۴.	`(∀x)(∃y)A(x, y)` اگر دامنه سخن را انسان‌ها بگیریم و A(x,y) را رابطه دوتایی y ،x را دوست دارد در جهان سخن تعبیر ‌کنیم، آنگاه تعبیر این فرمول گزاره «هر کسی کسی را دوست دارد.» خواهد بود.
۵.	`(AAy)A(y, a_۱)` اگر دامنه سخن را انسان‌ها بگیریم و گسترش آن را برای ثابت‌های فردی به مفاهیم مجرد بگیریم. A را رابطه دوتایی y ،x را دوست دارد در جهان سخن تعبیر ‌کنیم. همچنین تعبیر ثابت انفرادی a_۱ را انگاشت خوبی در نظر بگیریم، آنگاه تعبیر این فرمول گزاره «هر کسی خوبی را دوست دارد.» خواهد بود.
۶.	`(∀x_۱)(A(x_۱)` `⇒` `¬((∃x_۲)B(x_۲) ∧ C(x_۱, x_۲)))` اگر دامنه سخن را انسان‌ها بگیریم و A(x_۱) و B(x_۱) و C(x_۱,x_۲) را در زبان فارسی به ترتیب به متقلب، آزمون و موفق تعبیر ‌کنیم، آنگاه تعبیر این فرمول گزاره «هیچ متقلبی همیشه موفق نیست.» خواهد بود.
۷.	`(∀x)(∀y)``(``(H(x)∧H(y)∧ ¬E(x, y)``⇒``(∃p)``(P(p)∧(B(x, p)∧¬B(y, p)))` `)` اگر دامنه سخن را انسان‌ها بگیریم و H(x) و P(x) و B(x,y) و E(x,y) را به ترتیب به انسان بودن، ویژگی-بودن، ویژگی داشتن (`x` دارای ویژگی `y` است) و مساوی بودن تعبیر ‌کنیم، آنگاه تعبیر این فرمول گزاره «هیچ دو انسانی در همه ویژگی‌ها مشترک نیستد.» خواهد بود.
۸.	`(∀e)(∀c)(E(e)∧C(c, e)` ⇒ `P(c, e))` یک تعبیر این فرمول می‌تواند این باشد که برای هر رویداد 'e' و علت 'c'، اگر 'c' علت 'e' باشد، پس 'c' مقدم بر 'e' است.↝ [E - رویداد؛ C - علت؛ P- تقدم].
۹.	`(∀x)(∀y)(H(x)∧K(x, y)` ⇒ `B(x, y))` یک تعبیر این فرمول می‌تواند این باشد که کسی که چیزی را می‌داند به آن باور دارد. [H: انسان؛ K: دانش؛ B: باور].
۱۰.	تمایز متغیر آزاد و پابند در فرمول و تعبیر آن (۱) `(∀x)(P(x) ⇒ L(x, y))` در این فرمول متغیر "`x`" یک متغیر پابند است که محدوده آن، یعنی `obrace(P(x) → L(x, y))`، در قلمرو سور عمومی (∀) است. ولی متغیر "`y`" آزاد است زیرا با سوری محدود به کمیتی نشده است. اگر دامنه تعبیر را مجموعه انسان‌ها بگیریم، محمول "`P`" را رابطه یکتایی انسان بودن و محمول دو جایبانی "`L`" را رابطه دوتایی دوست داشتن تعبیر کنیم آنگاه تمایز پابند بودن "`x`" و آزاد بودن "`y`" در این فرمول آشکار می‌کند که این فرمول طبق این تعبیر مدعی است که هر شخص "`x`" دوستدار یک شخص "`y`" خاص و در عین حال نامشخص است (یعنی، یک "`y`" اختیاری).
۱۱.	تمایز متغیر آزاد و پابند در فرمول و تعبیر آن (۲) `(∃x)(Swan(x) ∧ Black(x))` در این فرمول متغیر "`x`" یک متغیر پابند است، که نشان می‌دهد این فرمول مدعی وجود حداقل یک قوی سیاه است. پابند بودن "`x`" به این معنی است که برآورد آن در تعبیر وابسته به یک گمارش (تخصیص) بیرونی نیست، بلکه به وجود چنین شیء در دامنه تعبیر↝ بستگی دارد. در این فرمول هیچ متغیر آزاد وجود ندارد، بنابراین درستی گزاره بر مبنای ساختار درونی عالم سخن (دامنه تعبیر) ارزیابی می‌شود. به عبارت دیگر، برای برآورد یک فرمول به عنوان درست یا نادرست، مقادیر متغیرهای آزاد آن باید در دامنه تعبیر مشخص یا فرض شوند. از سوی دیگر، متغیرهای پابند با توجه به سورهای پیوند دهنده آنها تعبیر می‌شوند و برآورد آنها به یک تخصیص بیرونی بستگی ندارد. این ترسیم واضح امکان تعبیر و برآورد دقیق فرمول‌ها را فراهم می‌کند.
۱۲.	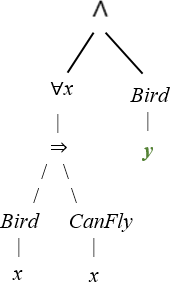تمایز متغیر آزاد و پابند در فرمول و تعبیر آن (مورد خاص ۳) `(∀x )(Bird(x) ⇒ CanFly(x)) ∧ Bird(y)` در این فرمول همه رویدادهای متغیر "`x`" پابند است و تنها رویداد متغیر "`y`" آزاد است. برگردان این فرمول به فارسی ساده عبارت است از «همه پرندگان می‌توانند پرواز کنند و مورد خاصی، که به عنوان "`y`" از آن یاد ‌شود، به عنوان یک پرنده شناخته می‌شود». این برگردان تمایز بین قانون کلی («همه پرندگان می‌توانند پرواز کنند») و نمونه خاص را نشان می‌دهد و به طور ضمنی این مفهوم منطقی را تأیید می‌کند که "`y`" می‌تواند بر اساس قانون کلی پرواز کند، حتی اگر این نتیجه خاص به طور مستقیم در عبارت برگردان شده بیان نشده باشد.