منطق محمولات: زبان، تعبیر و مدل (۲)
منطق و فرامنطق
درآمد به منطق
منطق محمولات: زبان، تعبیر و مدل (۲)
۱- مقدمه | ۹- درستی، نادرستی و صدق‌پذیری (Truth, falsity, and satisfaction) |
۲- زبان‌های مرتبه اول و تعبیر آنها: صدق‌پذیری و صدق: مدل | ۱۰- احکام تعبیر و صدق |
۳- تعریف: زبان مرتبه اول ℒ | ۱۱- رابطه و ویژگی (Relation and Property) |
۴- تعبیر زبان مرتبه اول ℒ | ۱۲- تمرین و اثبات احکام↧ |
۵- تمرین | ۱۳- انگاشت‌های «منطقاً معتبر»، «استلزام منطقی» و «نتیجه منطقی» |
۶- ساختار (Structure) | ۱۴- برخی احکام |
۷- صدق‌پذیری (Satisfiability) | ۱۵- تمرین بیشتر و حل برخی |
۸- تعریف استقرایی صدق کردن (برآوردن - Satisfaction) |
مگر در مواردی که با نماد "" مشخص شده باشد، محتوای ارائه شده در این یادداشت از مرجع زیر برگرفته و برگردان شده است.
Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. p. 45-60.
■ مقدمه
با تکیه بر یادداشت قبل، منطق محمولات و تعبیر آن، این فصل به قلمروهای پیچیده زبان، تعبیر، صدق و مدل می‌پردازد. ما بر مفهوم صدق‌پذیری (Satisfiability)، آنگونه که توسط آلفرد تارسکی ارائه شده است، تمرکز خواهیم کرد. درک شهودی تعبیر و صدق‌پذیری را که از یادداشت قبل به دست آوردیم، اکنون صوری‌شده و دقیق ارائه می‌شود.
■ زبان‌های مرتبه اول و تعبیر آنها: صدق‌پذیری و صدق: مدل
فرمول‌های خوش-ساخت تنها زمانی معنا پیدا می‌کنند که تعبیری برای نمادها ارائه شود. ما در پی تعبیر فرمول‌هایی هستیم که نمادهای آنها از یک زبان خاص آمده باشند. از این جهت، ما اینجا یک زبان مرتبه اول* را تعریف خواهیم کرد.
*- صفت «مرتبه اول» برای تمایز زبان‌هایی که در اینجا بررسی می‌کنیم از زبان‌هایی است که در آنها محمول‌هایی هستند که محمولات یا توابع دیگری را به عنوان آرگومان در خود دارند یا در آنها کاربرد سور برای حروف محمولی یا حروف تابعی (یا هر دو) مجاز است. بیشتر تئوری‌های ریاضی را می‌توان در زبان‌های مرتبه اول صوری کرد، اگرچه ممکن است برخی از محتوای شهودی آن تئوری‌ها از بین برود. (ما در قسمت‌های بعد زبان‌های مرتبه دوم را مورد بحث قرار خواهیم داد). نمونه‌هایی از زبان‌های مرتبه بالاتر نیز در گودل (۱۹۳۱، تارسکی (۱۹۳۳)، چرچ (۱۹۴۰)، لیوانت (۱۹۹۴)، و بنتام (۱۹۸۳) مورد مطالعه قرار گرفته‌اند. تفاوت بین تئوری‌های مرتبه اول و مرتبه بالاتر در کرکران (۱۹۸۰) و شاپیرو (۱۹۹۱) بررسی شده است.↧
• Gödel, K. (1931) Ueber formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme. I. Monatsh. Math. Phys., 38, 173–198 (English translation in Davis, 1965).
• Tarski, A. (1933) Einige Berachtungen über die Begriffe der ω-Widerspruchsfreiheit und der ω-Vollstandigkeit. Monatsh. Math. Phys., 40, 97–112.
• Church, A. (1940) A formulation of the simple theory of types. JSL, 5, 56–68.
• Leivant, D. (1994) Higher order logic. Handbook of Logic in Artificial Intelligence and Logic Programming, Vol. 2 (eds. D.M. Gabbay, C.J. Hogger, and J.A. Robinson), Clarendon Press, pp. 229–321.
• van Benthem, J. and K. Doets. (1983) Higher-order logic. HPL, I, 275–330.
• Corcoran, J. (1980) Categoricity. Hist. Philos. Log., 1, 187–207.
• Shapiro, S. (1991) Foundations without Foundationalism: A Case for Second-order Logic. Oxford University Press.
■ تعریف: زبان مرتبه اول ℒ
زبان مرتبه اول ℒ دارای نمادهای زیر است:
نشانه‌های نگارشی: پرانتز چپ ")"، پرانتز راست "(" و کاما ",". [نشانه‌های نگارشی بطور تاکیدی ضروری نیستند. با بازتعریف انگاشته‌های ترم و wff می‌توان بی‌نیار از آنها شد. با این حال، استفاده از آنها خواندن و فهم فرمول‌ها را آسان‌تر می‌کنند]
به هر تعداد دلخواه زیاد متغیرهای انفرادی شمارش پذیر `x_۱, x_۲, ...`.
یک مجموعه متناهی یا شمارش پذیر (یا تهی) از حروف تابعی.
یک مجموعه متناهی یا شمارش پذیر (یا تهی) از ثابت‌های انفرادی.
یک مجموعه ناتهی از حروف محمولی.
منظور از یک ترم در ℒ یک ترم است که نمادهای آن از نمادهای ℒ باشند.
منظور از یک wff در ℒ یک wff است نمادهای آن از نمادهای ℒ باشند.
بنابراین، در زبان ℒ ممکن است برخی یا همه حروف تابعی و ثابت‌های انفرادی وجود نداشته باشند، و برخی (اما نه همه) حروف محمولی ممکن است وجود نداشته باشند. ثابت‌های انفرادی، حروف تابعی، و حروف محمولی زبان ℒ ثابت‌های غیرمنطقی↝ ℒ نامیده می‌شوند. زبان‌ها مطابق با موضوع مورد بحثی که می‌خواهیم بررسی کنیم طراحی می‌شوند. یک زبان برای حساب ممکن است دارای حروف تابعی برای جمع و ضرب و یک حرف محمولی برای تساوی باشد، در حالی که زبانی برای هندسه می‌تواند دارای حروف محمولی برای برابری و انگاشت‌های نقطه و خط باشد، اما اصلاً حروف تابعی نداشته باشد.
■ تعبیر زبان مرتبه اول ℒ
گیریم ℒ یک زبان مرتبه اول باشد. یک تعبیر M از ℒ شامل عناصر زیر است.
یک مجموعه ناتهی D با نام دامنه تعبیر.
برای هر حرف محمولی `A_j^n` در ℒ انتساب یک رابطه n-تایی `(A_j^n)^M` در D. [تعبیر یک محمول n-جایبانی معین در زبان ℒ تحت تعبیری به نام M که دامنه سخن آن مجموعه D است، عبارت است از یک رابطه n-تایی معین در مجموعه D].
برای هر حرف تابعی `f_j^n` در ℒ انتساب یک تابع n-تایی `(f_j^n)^M` در D. [یعنی، یک تابع از `D^n` در D].
برای هر ثابت انفرادی `a_i` در ℒ انتساب عنصر تثبیت شده `(a_i)^M` در D.
تحت چنین تعبیری، متغیرها در دامنه مجموعه D در نظر گرفته می‌شوند و ¬، ⇒ و سورها معانی معمول خود را دارند. به یاد داشته باشید که یک رابطه n-تایی در D را می‌توان یک زیرمجموعه از `D^n`، یعنی مجموعه تمام n گانه‌های D، در نظر گرفت. برای مثال، اگر D مجموعه انسانها باشد، آنگاه رابطه "پدر بودن" را می‌توان به عنوان مجموعه همه دوتایی‌های مرتب 〈x, y〉 در نظر گرفت به قسمی که x پدر y باشد.
برای یک تعبیر معین از زبان ℒ، یک فرمول ℒ بدون متغیرهای آزاد، که فرمول بسته یا جمله نامیده می‌شود، بیانگر گزاره‌ای است که درست یا نادرست است. در حالی که یک فرمول ℒ با متغیرهای آزاد، که فرمول باز نامیده می‌شود، ممکن است برای برخی مقادیر دامنه تصدیق شود (یعنی درست باشد) و برای بقیه مقادیر تصدیق نشود (یعنی نادرست باشد).
مثال:
فرمول های زیر را در نظر بگیرید:
دامنه تعبیر را مجموعه همه اعداد صحیح مثبت و معنی و `A_1^2(y,z)` را `y ≤ z` می‌گیریم.
در این صورت فرمول ۱ عبارت از "`x_1 ≤ x_2`" خواهد بود، که توسط همه زوج مرتب‌های `〈a, b〉` از اعداد صحیح مثبت به قسمی که `a ≤ b` برآورده می‌شود.
فرمول ۲ بیانگر عبارت "برای همه اعداد صحیح مثبت `x_2`، به قسمی که داشته باشیم `x_1 ≤ x_2`" خواهد بود، که فقط با عدد صحیح ۱ برآورده می‌شود*. [* به زبان فارسی معمول می‌گوییم: `x_2` کوچکتر یا مساوی هر عدد صحیح مثبت است.]
فرمول ۳ یک جمله درست است که می‌گوید کوچکترین عدد صحیح مثبت وجود دارد. اگر دامنه تعبیر را مجموعه اعداد صحیح در نظر بگیریم، فرمول ۳ نادرست خواهد بود.
■ تمرین (۱۰.۲ - ۱۱.۲):
۱۰.۲- برای فرمول‌های زیر و برای تعبیرهای داده شده، مشخص کنید که فرمول‌ها (اگر دارای متغیرهای آزاد هستند) به چه مقادیری برآورده می‌شوند یا (اگر فرمول‌های بسته هستند) درست یا نادرست هستند.
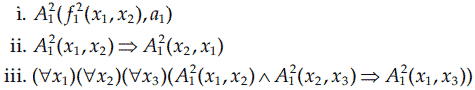
آ. دامنه مجموعه اعداد صحیح مثبت است، `A_1^2(y,z)` عبارت از `y≥z` و `f_1^2(y,z)` عبارت از `y·z` و `a_1` برابر ۲ است.
حل آ. فرمول (i) توسط زوج مرتب `〈x_1, x_2〉`که در آن `x_1` و `x_2` عدد صحیح مثبت باشند و داشته باشیم `x_1.x_2≥2` برآورده می‌شود.
فرمول (ii) توسط زوج مرتب‌های `〈x_1, x_2〉` از اعداد صحیح مثبت برآورده می‌شود به قسمی که یا `x_1<x_2` (وقتی مقدم نادرست است) یا `x_1=x_2` (وقتی که مقدم و تالی هر دو درست هستند).
فرمول (iii) درست است.
ب. دامنه مجموعه اعداد صحیح است، `A_1^2 (y, z)` به معنی `y=z`، و `f_1^2(y,z)` عبارت از `y + z` و `a_1` برابر ۰ است.
ج. دامنه مجموعه اعداد صحیح است، `A_1^2(y,z)` رابطه `y⊆z` و `f_1^2(y,z)` عبارت از `y∩z` و `a_1` مجموعه تهی (∅) است.
۱۱.۲- ادعاهای را که با فرمول‌ها و تعبیرهای آمده در زیر معین شده‌اند به زبان فارسی بیان کنید.
آ.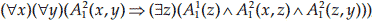 
که در آن دامنه `D` مجموعه اعداد حقیقی و `A_1^2(x,y)` رابطه x<y و `A_1^1(z)` به معنی `z` یک عدد گویا است.
حل آ. بین هر دو عدد حقیقی عددی گویا وجود دارد.
ب.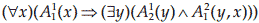 
که در آن دامنه `D` مجموعه روزها و انسانها است. `A_1^1(x)` به معنی `x` روز است، `A_1^2(y)` به معنی `y` فوتبالیست است و `A_1^2(y,x)` به معنی `y` در روز `x` به دنیا آمده است.
پ.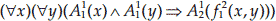 
که در آن دامنه `D` مجموعه اعداد صحیح و `A_1^1(x)` به معنی `x` فرد است، `A_2^1(x)` به معنی `x` زوج است و `f_1^2(x,y)` عبارت از `x+y` است.
ت. دامنه `D` برای فرمول‌های زیر مجموعه همه انسانها است. `A_1^2(u,v)` به معنی `u`، `v` را دوست دارد است.
ث.
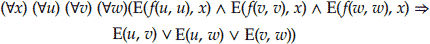
که در آن دامنه `D` مجموعه اعداد حقیقی و `A_1^1(x)` به معنی `x` فرد است، `E(x,y)` به معنی `x=y` است و `f` نشانگر عمل ضرب است.
ج.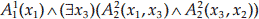 
که در آن دامنه `D` مجموعه انسانها و `A_1^1(u)` به معنی زن بودن و `A_2^2(u,v)` به معنی `u` پدر یا مادر بودن `v` است.
چ. 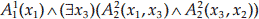که در آن دامنه `D` مجموعه اعداد حقیقی است و `A_1^1(u)` به معنی منفی بودن `u` است و `A_1^2(u)` به معنی مثبت بودن `u` است.
■ ساختار (Structure)
یک زبان صوری مانند `ℒ` یک چارچوب نحوی را فراهم می‌کند. این چهار چوب روندی را میسر می‌کند تا به معنادهی به عناصر این زبان در پیوند با مجموعهای از اشیاء مورد نظر دست یافت. به چنین چهارچوبی در منطق «ساختار» گفته می‌شود.
به عبارت دیگر، این چارچوب قواعد و نمادهایی را معرفی می‌کند که امکان ساخت عبارات و جمله‌‌ها را میسر کند. ما برای پیوند این عناصر نحوی به دنیای واقعی یا هستی‌های انتزاعی، عناصر این زبان را در یک زمینه خاص تعبیر می‌کنیم. این کار با پیوند دادن نمادها و عبارات `ℒ` با مجموعهای از اشیاء یا هستی‌های مورد پرسش به دست می‌آید. چنین پیوندی از طریق یک «ساختار» در منطق میسر می‌شود، که به طور روشمند معانی را بر اساس عناصر یک دامنه به نمادهای `ℒ` اختصاص می‌دهد. در زیر بطور دقیق تعریفی از چنین ساختاری آمده است:
یک ساختار عبارت است از سه تایی مرتب `〈ℒ,D,I〉` که در آن:
`ℒ` یک زبان صوری است که شامل مجموعهای از نمادها (مانند نماد محمولی، نماد تابعی و نمادهای ثابت‌ها) و احتمالاً برخی قواعد ساخت فرمول است.
`D` یک مجموعه ناتهی است که اغلب به عنوان دامنه (نیز جهان سخن) ساختار نامیده می‌شود. `D` مجموعهای است که تعبیر زبان `ℒ` بر آن تعبیر می‌شود.
`I` تابع تعبیر (یا فقط تعبیر) به همراه `D` به عنوان دامنه تعبیر `I` است. تابع `I` یک نگاشت از عناصر زبان (`ℒ`) در `D^n` است که به عناصر `ℒ` معانی مصداقی در `D^n` را به شرح زیر می‌گمارد:
از هر نماد محمولی n-جایبانی در `ℒ` به یک رابطه n-تایی در `D^n`.
از هر نماد تابعی n-جایبانی در `ℒ` به یک تابع n-متغیری از `D^n` در `D`.
از هر نماد ثابت در `ℒ` به یک عنصر مشخص و متمایز در `D`.
این نگاشت (`I`) پایه معنایی را برای تعبیر نمادهای `ℒ` در ساختار تعریف شده توسط دامنه `D` فراهم می‌کند. چنین ساختاری را نیز به صورت `ℒ`-ساختار (ℒ-structure) می‌نویسند.
■ صدق‌پذیری (Satisfiability)
انگاشت‌های صدق‌پذیری و صدق به طور شهودی آشکار هستند↝، اما به پیروی از تارسکی (۱۹۳۶)، ما نیز در اینجا تعریف دقیقی برای آنها ارائه خواهیم کرد. چنین تعریفی برای اثبات دقیق بسیاری از نتایج فرا-ریاضی↰ (Metamathematical) ضروری است.
صدق‌پذیری یک انگاشت بنیادی است که بر اساس آن، انگاشت صدق تعریف خواهد شد. علاوه بر این، به جای صحبت از n-گانه‌های اشیاء که یک فرمول دارای n متغیر آزاد را صدق‌پذیر می‌کند، از نقطه نظر فنی بسیار آسان‌تر است که به طور یکنواخت از دنباله‌های نامتناهی-شمارا صحبت کنیم.
هنگام کار در منطق و فرمول‌های پیچیده،
در نظر داشتن یک دنباله شمارش‌پذیر امکان یک رویکرد یکسان برای تحلیل و ساختن برهان را فراهم می‌کند. این ممکن می‌کند تا نیاز نباشد مدام در پی تطبیق با تعداد متغیرهای مختلف و تنظیم آنها بود. می‌توان جدا از اینکه فرمولی چند متغیر دارد، تکنیک یکسانی را اعمال کرد تا کار ساده‌تر و کمتر در معرض خطا باشد.
گیریم `β` یک فرمول، که دارای متغیرهای آزاد `(x_[j۱], x_[j۲], x_[j۳], ...x_[jn])` است و نیز `j_۱<j_۲< j_۳,...,<j_n`، باشد.
آنچه می‌خواهیم این است که یک دنباله شمارا-نامتناهی `s=(s_۱,s_۲,s_۳,...)` باید به عنوان برآورنده (satisfying) فرمول `β` در نظر گرفته شود، اگر n-گانه `〈s_[j۱], s_[j۲], s_[j۳], ...s_[jn]〉` به معنای معمول در `β` صدق کند. (به عبارت دیگر، `β` توسط s صدق‌پذیر - satisfiable - باشد).
دو جمله «دنباله `s` فرمول `β` را برمی‌آورد.» و «دنباله `s` در فرمول `β` صدق می‌کند.» به طور معادل به کار برده می‌شوند.
برای مثال، یک دنباله نامتناهی-شمارا
`(s_۱,s_۲, s_۳,s_۴, s_۵,s_۶,...)`
از اشیاء در دامنه تعبیر M، برای فرمول `A_۱^۲(x_۲,x_۵)` صدق‌پذیر است، اگر و فقط اگر دوتایی مرتب `〈s_۲, s_۵〉` در رابطه `(A_۱^۲)^M`باشد که در تعبیر M به حرف محمولی `A_۱^۲` اختصاص داده شده است.
گیریم M یک تعبیر زبان ℒ و D دامنه M باشد. نیز، Σ مجموعه همه دنباله‌های شمارا نامتناهی عناصر D باشد.
برای فرمول β در ℒ، باید تعریف کنیم اینکه یک دنباله در Σ، به فرض `s=(s_۱, s_۲, ...)`، تحت M در β صدق می‌کند (به عبارت دیگر، دنباله s تحت M فرمول β را برمی‌آورد) به چه معنا است.
در مرحله مقدماتی، برای یک دنباله `s` معین در Σ باید یک تابع `s^***` تعریف کنیم که به هر ترم t از ℒ یک عنصر `s^***(t)` در D اختصاص دهد. به عبارت دیگر، `s^***` تابعی است که توسط دنباله `s` معین می‌شود.
اگر t یک متغیر انفرادی به فرض `x_j`، باشد آنگاه مقدار `s^***(t)` را `s_j` (عنصر j-ام دنباله s) می‌گیریم.
اگر t یک ثابت انفرادی به فرض `a_j`، باشد آنگاه مقدار `s^***(t)` را تعبیر `(a_j)^M` می‌گیریم.
اگر `f_k^n` یک حرف تابعی باشد و `(f_k^n)^M` عمل متناظر آن در D باشد، نیز `t_۱,...,t_n` ترم باشند، آنگاه:
`s^***(f_k^n(t_۱,...,t_n))` `=` `(f_k^n)^M(s^***(t_۱),...,s^***(t_n))`.
به طور شهودی، `s^***(t)` عنصر D است که با جایگزین کردن، برای هر j، یک نام `s_j` برای همه رویدادهای `x_j` در `t`† و سپس انجام اعمال تعبیر مربوط به حرف تابعی t به دست می‌آید.
†- مراد از «یک نام `s_j` برای همه رویدادهای `x_j` در `t` جایگزینی هر متغیر `x_j` در ترم `t` با عنصر خاص `s_j` از دامنه D است.
برای مثال، اگر t عبارت از `f_۲^۲(x_۳, f_۱^۲(x_۱,a_۱))` باشد و اگر دامنه تعبیر مجموعه اعداد صحیح باشد، نیز `f_۲^۲` و `f_۱^۲` به ترتیب به عنوان ضرب و جمع معمولی و `a_۱` به عنوان ۲ تعبیر شوند، آنگاه برای هر دنباله `s=(s_۱, s_۲, ...)` از اعداد صحیح، `s^***(t)` عدد صحیح `s_۳×(s_۱+۲)` است. و این واقعا چیزی نیست جز روش معمولی خواندن عبارات ریاضی.
■ روند محاسبه `s^***(t)`
با تکیه بر بحث ارائه شده، روند محاسبه تابع `s^***(t)` برای ترم t در زیر فهرست شده است:
جایگزینی متغیرهای t،
تعبیر حروف تابعی و ثابت‌های انفرادی موجود در t،
برآورد t پس از مرحله ۱ و ۲.
اکنون می‌توانیم انگاشته‌های درست و نادرست (صدق و کذب) یک فرمول را برای یک تعبیر معین تعریف کنیم.
تعریف استقرایی صدق کردن (برآوردن - Satisfaction)
اینجا تعریف صدق کردن (برآوردن - Satisfaction) که تعریفی استقرایی است را ادامه می‌دهیم.
اگر β فرمول اتمی `A_k^n(t_۱,...,t_n)` و `(A_k^n)^M` رابطه n-تایی نظیر آن [در D] باشند، آنگاه یک دنباله `s=(s_۱, s_۲, ...)` در β صدق می‌کند (یا به عبارت دیگر، دنباله `s` فرمول β را برمی‌آورد) اگر و تنها اگر
`(A_k^n)^M(`𝒮*(t۱)`,... ,`𝒮*(tn)`)`
— یعنی n-گانه `〈`𝒮*(t۱)`,... ,`𝒮*(tn)`〉` در رابطه `(A_k^n)^M` باشد.
مثال ۱- اگر دامنه تعبیر مجموعه اعداد حقیقی باشد، تعبییر `A_۱^۲` رابطه `≤`، و تعبیر `f_۱^۱` تابع `e^x` باشند، آنگاه دنباله `s=(s_۱, s_۲, ...)` از اعداد حقیقی در `A_۱^۲(f_۱^۱(x_۲),x_۵)` صدق می‌کند اگر و فقط اگر `e^(s_۲)≤s_۵`.
مثال ۲- اگر دامنه تعبیر مجموعه اعداد صحیح باشد، تعبیر `A_۱^۴(x,y,u,v)` رابطه `x.v=u.y` و تعبیر `a_۱` عدد ۳ باشد آنگاه دنباله `s=(s_۱, s_۲, ...)` از اعداد صحیح در `A_۱^۴(x_۳,a_۱,x_۱,x_۳)` صدق می‌کند اگر و فقط اگر `(s_۳)^۲=۳s_۱`.
(دنباله) s در β صدق می‌کند اگر و فقط اگر s در ¬β صدق نکند.
(دنباله) s در β ⇒ ς صدق می‌کند اگر و فقط اگر s در β صدق نکند یا s در ς صدق کند.
(دنباله) s در `(∀x_i)β` صدق می‌کند اگر و فقط هر دنباله که حداکثر در مولفه iام از s متفاوت است در `β` صدق کند.
به عبارت دیگر، دنباله `s=(s_۱, s_۲,...,s_i,...)` در `(∀x_i)β` صدق می‌کند اگر و فقط اگر برای هر عنصر c در دامنه تعبیر، دنباله `s=(s_۱, s_۲,...,c,...)` در `β` صدق کند. در اینجا، `s=(s_۱, s_۲,...,c,...)` دنباله بدست آمده از `s=(s_۱, s_۲,...,s_i,...)` را با جایگزینی مولفه iام، یعنی `s_i`، با `c` نشان می‌دهد. همچنین توجه داشته باشید که اگر s در `(∀x_i)β` صدق کند، آنگاه s به عنوان یک مورد خاص در `β` می‌کند.
به طور شهودی، دنباله `s=(s_۱, s_۲,...)` در فرمول β صدق می‌کند (یا بگونه دیگر، دنباله `s=(s_۱, s_۲,...)` فرمول β را برمی‌آورد) اگر و فقط اگر برای هر i، تمام رویدادهای آزاد `x_i` (اگر وجود دارد) در β را با نمادی که نشان دهنده `s_i` است، جایگزین کنیم، گزاره حاصل تحت تعبیر داده شده درست (صادق) باشد.
اکنون می‌توانیم پنداشت درستی و نادرستی wffها را برای یک تعبیر معین تعریف کنیم.
■ درستی، نادرستی و صدق‌پذیری (Truth, falsity, and satisfaction)
■ صدق (درستی)
■ احکام تعبیر و صدق
درخور بودن تعریف ما از صدق با این واقعیت تقویت می‌شود که می‌توانیم تمام ویژگی‌های مورد انتظار I تا XI در زیر را از انگاشت‌های درستی، نادرستی و صدق‌پذیری استخراج کنیم. برهان‌ها به صراحت ارائه نشده‌اند و به خواننده واگذار می‌شوند (نیز می‌توان در پاسخ به تمرین ۲.۱۲ آنها را یافت). اگر کسی بخواهد فقط درک شهودی و معمول انگاشت‌های درستی، نادرستی و صدق‌پذیری را به کار ببرد، بسیاری از نتایج نیز آشکار هستند.
چنین نیست که `⊧_M β` و هم `⊧_M¬β` هر دو برقرار باشند، به عبارت دیگر، فرمولی نیست که تحت M بتواند درست و هم نادرست باشد.
اگر `⊧_M β` و `⊧_M β⇒ς` آنگاه `⊧_M ς`.
تعبیر M با دامنه D را در نظر بگیرید. در این صورت:
(دنباله) s در β ∧ ς صدق می‌کنند اگر و فقط اگر s در β صدق کند و s در ς صدق کند.
(دنباله) s در β ∨ ς صدق می‌کنند اگر و فقط اگر s در β صدق کند یا s در ς صدق کند.
(دنباله) s در β ⇔ ς صدق می‌کنند اگر و فقط اگر s در β و هم در در ς صدق کند یا نه در β و نه در در ς صدق کند.
بخاطر داشته باشید β∧ς, β∨ς, β⇔ς و `(∃x_i)B` به ترتیب کوتاه شده برای ¬(β⇒¬ς), ¬β⇒ς, (β⇒ς)∧(ς⇒β) و `¬(∀x_i)¬β` هستند.
s در `(∃x_i)β` صدق می‌کند اگر و فقط اگر دنباله s' که حداکثر در مولفه iام با s متمایز است وجود داشته باشد آنگونه که s' در `(∃x_i)β` صدق کند.
[به عبارت دیگر، `s=(s_۱, s_۲,...,s_i,...)` در `(∃x_i)β` صدق می‌کند اگر و فقط اگر عنصر c در دامنه D باشد به قسمی که دنباله `(s_۱, s_۲,...,c,...)` در `β` صدق کند].
`⊧_M β` اگر و فقط اگر `⊧_M (∀x_i)β`. [به عبارت دیگر، فرمول `β` درست است اگر و فقط اگر بستار عمومی آن درست باشد].
تعریف: بستار فرمول (closure of formula):
بستار فرمول β (یا به عبارت بهتر بستار عمومی فرمول) عبارت از فرمول بسته‌ای است که از β با پیشوند کردن آن در سور عمومی آن دسته از متغیرهای آزاد β به ترتیب نزولی اندیس‌های آنها از β به دست آمده باشد.اگر β هیچ متغیر آزاد نداشته باشد، بستار β به عنوان خود β تعریف می‌شود.
برای مثال، اگر `β` فرمول `A_۱^۲(x_۳,x_۵)⇒¬(∃x_۲)A_۱^۳(x_۱,x_۲,x_۳)` باشد آنگاه بستار آن به قرار `(∀x_۵)(∀x_۳)(∀x_۲)(∀x_۱)β` خواهد بود. بنابراین، می‌توان از (VI) نتیجه گرفت که فرمول `β` درست است اگر و فقط اگر بستار عمومی آن درست باشد.
هر مورد از توتولوژی برای هر تعبیری درست است. (موردی از یک صورت گزاره‌ای عبارت است از فرمولی که با جایگزین کردن فرمول‌ها به جای همه حروف گزاره‌ای، با جایگزینی همه حروف گزاره‌ای یکسان با همان فرمول، از صورت گزاره‌ای بدست می‌آید. برای مثال، یک مورد `A_۱⇒¬A_۲∨A_۱` عبارت است از `A_۱^۱(x_۲)⇒(¬(∀x_۱)A_۱^۱(x_۱)∨ A_۱^۱(x_۲))`.
اگر متغیرهای آزاد فرمول β (در صورت وجود) در فهرست `x_(i_۱),...,x_(i_k)` باشند و اگر دنباله‌های s و s' دارای مولفه‌های یکسان در موقعیت‌های `i_۱`ام تا `i_k`ام باشند، آنگاه s در فرمول β صدق می‌کند (s فرمول β را برمی‌آورد) اگر و فقط اگر s' در فرمول β صدق کند.
راهنمایی: از استقرا در تعداد رابط‌ها و سورها در β استفاده کنید.
ابتدا این لم را ثابت کنید: اگر متغیرهای ترم t در فهرست `x_(i_۱),...,x_(i_k)` باشند و اگر s و s' در موقعیت‌های `i_۱`ام تا `i_k`ام مولفه‌های یکسانی داشته باشند، آنگاه
s*(t) = (s′)*(t) .
به ویژه، اگر t اصلاً هیچ متغیری نداشته باشد برای هر دنباله s و s' داریم
s*(t) = (s′)*(t).
اگرچه طبق (VIII)، یک فرمول خاص مانند β با k متغیر آزاد ضرورتاً فقط با k-گانه‌ها برآورده می‌شود یا نمی‌شود (صدق‌پذیر است یا چنین نیست) و نه با دنباله‌های نامتناهی-شمارا (نیاز به چنین دنباله‌ها نیست)، اما برای یک رویکرد کلی در باره صدق‌پذیری آسان‌تر خواهد بود به جای دنباله‌های متناهی با دنباله‌های نامتناهی-شمارا سروکار داشته باشد. اگر بخواهیم صدق‌پذیری را با استفاده از دنباله‌های متناهی تعریف کنیم، شرایط ۳ و ۴ تعریف صدق‌پذیری بسیار پیچیده‌تر خواهد شد.
■ رابطه و ویژگی (Relation and Property)
فرض کنید `x_[i_۱], x_[i_۲], x_[i_۳], ...,x_[i_n]` عبارت از `k` متغیر متمایز به ترتیب افزایشی اندیس‌ها باشند. گیریم `β(x_[i_۱], x_[i_۲], x_[i_۳], ...,x_[i_n])` فرمولی باشد که فقط متغیرهای `x_[i_۱], x_[i_۲], x_[i_۳], ...,x_[i_n]` را بعنوان متغیر آزاد دارد. اکنون، مجموعه k-گانه‌های `〈b_۱,...,b_k〉` از عناصر دامنه D را در نظر بگیرید، به قسمی که هر دنبالهای با عناصر `b_۱,....,b_k` که به ترتیب در موقیت‌های `i_۱`ام تا `i_k`ام آن قراردارند، فرمول `β(x_[i_۱], x_[i_۲], x_[i_۳], ...,x_[i_k])` را برآورند. در این صورت، این مجموعه را رابطه (یا ویژگی برای وقتی که k=۱ است) تعبیر تعریف‌شده توسط β می‌نامند.
با گسترش واژگان خود، می‌گوییم که k-گانه `〈b_۱,...,b_k〉` رابطه `β(x_[i_۱], x_[i_۲], x_[i_۳], ...,x_[i_k])` ر تحت تعبیر M برآورده می‌کند. این را به صورت `⊧_Mβ[b_1,...,b_k]` می‌نویسیم. این پنداشت گسترده از صدق‌پذیری با پنداشت شهودی اولیه مطابقت دارد.
مثال ۱.
اگر دامنه D در تعبیر M مجموعه انسانها باشد و `A_۱^۲(x,y)` با x برادر y است و `A_۲^۲(x,y)` با x مادر y است تعبیر شود آنگاه رابطه دوتایی در D متناظر با فرمول:
`β(x_۱,x_۲):` `(∃x_۳)(A_۱^۲(x_۱,x_۳)∧A_۲^۲(x_۳,x_۲))`
رابطه دایی-بودن تعبیر خواهد شد. در این صورت `⊧_M β[b,c]` تنها و فقط تنها زمانی برقرار است که b دایی c باشد.
مثال ۲.
اگر دامنه تعبیر اعداد صحیح مثبت باشد، تعبیر `A_۱^۲` از قرار = باشد، نیز تعبیر `f_۱^۲` ضرب و تعبیر `a_۱` عدد ۱ در نظر گرفته شود، آنگاه فرمول:
`β(x_۱):` `¬A_۱^۲(x_۱,a_۱)∧(∀x_۲)` `((∃x_۳)A_۱^2(x_۱,f_۱^۲(x_۲,x_۳))⇒` `A_۱^۲(x_۲,x_۱)∨A_۱^۲(x_۲,a_۱))`
ویژگی عدد اول بودن را معین می‌کند. بنابراین `⊧_M β[k]` اگر و تنها اگر k یک عدد اول باشد.
مثال ۳.
اگر دامنه تعبیر اعداد صحیح، تعبیر `A_۱^۲` از قرار =، نیز تعبیر `f_۱^۲` ضرب باشد، آنگاه تعبیر فرمول:
`[(∃u)(A_۱^۲(f_۱^۲(x,u),y)]` `^^` `[(∃v)(A_۱^۲(f_۱^۲(x,v),z)]`
ازقرار «`x` مقسوم علیه مشترک `y , z` است.» خواهد بود.
اگر β فرمول بسته یک زبان ℒ باشد، برای هر تعبیر M، یا `⊧_M β` یا `⊧_M ¬β` - یعنی β برای M درست است یا β برای M نادرست است. [راهنمایی: استفاده از (VIII).] البته ممکن است β برای برخی از تعبیرها درست و برای برخی دیگر نادرست باشد. (به عنوان مثال، `A_۱^۱(a_۱)` را در نظر بگیرید. اگر M تعبیری باشد که دامنه آن مجموعه اعداد صحیح مثبت است، `A_۱^۱` به عنوان ویزگی اول بودن تعبیر شود و تعبیر `a_۱` به ۲ تعبیر شود، `A_۱^۱(a_۱)` درست است. اگر تعبیر را با تعبیر `a_۱` به ۴ تغییر دهیم، `A_۱^۱(a_۱)` نادرست می‌شود.)
اگر فرمول β بسته نباشد - یعنی اگر β دارای متغیرهای آزاد باشد - β ممکن است برای برخی تعبیرها نه درست و نه نادرست باشد. به عنوان مثال، گیریم `A_۱^۲(x_۱,y_۱)` یک فرمول باشد. تعبیری را در نظر می‌گیریم که در آن دامنه تعبیر مجموعه اعداد صحیح است و `A_۱^۲(y_۱,z_۱)` به عنوان `y<z` تعبیر می‌شود. در این صورت فقط آن دنباله‌های `s=(s_۱,s_۲,...)` از اعداد صحیح در β صدق می‌کند که `s_۱<s_۲`. از این رو، β برای این تعبیر نه درست است و نه نادرست. از سوی دیگر، فرمول‌هایی هستند که بسته نیستند، اما برای هر تعبیری درست یا نادرست هستند. یک مثال ساده، فرمول `A_۱^۱(x_۱)∨¬A_۱^۱(x_۱)` است که برای همه تعبیرها صادق است.
■ لم ۱
اگر `t` و `u` ترم و `s` یک دنباله در Σ باشد و`t'` از `t` با جایگزینی تمام رویدادهای `x_i` با `u` حاصل شده باشد، نیز`s'` از `s` با جایگزینی مولفه iام `s` با s*(u) بدست آمده باشد. در این صورت:
s*(t')=(s')*(t).
[راهنمایی: از استقرای طولی روی s* استفاده کنید].
■ لم ۲
گیریم ترم `t` برای متغیر `x_i` در `β(x_i)` آزاد باشد. آنگاه:
اگر `(∀x_i)β(x_i)` توسط دنباله `s` برآورده شود آنگاه `β(t)` توسط `s` برآورده خواهد شد.
اگر `β` شامل `x_i` آزاد نباشد آنگاه
`(AAx_i)(β⇒ς)⇒(β⇒(∀x_i)ς)`
برای هر تعبیری درست است.
اثبات:
۱. فرض می‌کنیم (XI) صحیح نیست. بنابراین فرمول:
`(∀x_i)(β⇒ς)⇒(β⇒(∀x_i)ς)`
برای برخی تعبیر درست نیست.
۲. پس، بنا بر شرط ۳ (تعریف صدق‌پذیری)، دنباله `s` وجود دارد به قسمی که `s` فرمول `(∀x_i)(β⇒ς)` را برمی‌آورد ولی `β⇒(∀x_i)ς` را برنمیآورد.
۳. از این (فرمول آخر در (۲)) و شرط ۳ (تعریف صدق‌پذیری)، دنباله `s` فرمول `β` را برمی‌آورد ولی `(∀x_i)ς` را برنمیآورد. بنابراین، از شرط ۴ (تعریف صدق‌پذیری)، دنباله `s'` که در مولفه iام از `s` متفاوت است وجود دارد به قسمی که `s'` فرمول `ς` را برنمیآورد.
۴. از آنجا که `x_i` نه در `(∀x_i)(β⇒ς)` و نه در `β` آزاد است و اینکه `s` هر دو این فرمول‌ها را برمی‌آورد، از VIII بدست می‌آید که`s'` هم `(∀x_i)(β⇒ς)` و هم `β` را نیز برمی‌آورد.
۵. چون `s'` فرمول `(∀x_i)(β⇒ς)` را برمی‌آورد پس بنا بر شرط ۴ (تعریف صدق‌پذیری)، `s'` فرمول `β⇒ς` را برخواهد آورد.
۶. و چون `s'` فرمول `β⇒ς` و `β` را برمی‌آورد، شرط ۳ (تعریف صدق‌پذیری) نتیجه می‌دهد که `s'` فرمول `ς` را برخواهد آورد، که این خلاف این است که `s'` فرمول ς را برنمیآورد. بنابراین، (XI) ثابت می‌شود.▢
■ تمرین و اثبات احکام↧
Mendelson, Elliott. Introduction to mathematical logic. 6th, ed, CRC Press, Taylor & Francis Group. 2015. 2.2. p 60 - 62.
۲.۱۲ صحت (I)–(X) را نشان دهید.
حل:
I.
دنباله `s` فرمول `¬β` را برمی‌آورد اگر و فقط اگر `s` فرمول `β` را برنیاورد. از این رو، هر دنباله `¬β` را برمی‌آورد اگر و فقط اگر دنبالهای نباشد که `β` را برآورد. یعنی `¬β` درست است اگر و فقط اگر `β` نادرست باشد.
II.
حداقل یک دنباله `s` در Σ وجود دارد. اگر `s` فرمول `β` را برآورد، `β` نمی‌تواند برای `M` نادرست باشد. اگر `s` فرمول `β` را برنیاورد، `β` نمی‌تواند برای `M` درست باشد.
III.
اگر دنباله `s` هم `β` و هم `β ⇒ ς` را برآورد، `s`، با توجه به شرط ۳ در تعریف صدق، `ς
` را برمی‌آورد.
V.
`s` فرمول `β∧ς` را برمی‌آورد اگر و فقط اگر `s` فرمول `¬(β ⇒¬ς)` را برآورد.
. . . اگر و فقط اگر `s` فرمول `β⇒¬ς` را برنیاورد.
. . . اگر و فقط اگر `s` فرمول `β` را برآورد اما `¬ς` را برنیاورد.
. . . اگر و فقط اگر `s` فرمول `β` و `s` فرمول `ς` را برآورد.
VI.
آ- `⊧_M β` را فرض بگیرید. پس هر دنبالهای `β` را برمی‌آورد. به ویژه، هر دنبالهای که با دنباله `s` حداکثر در مکان `i`ام متمایز است، `β` را برمی‌آورد. بنابراین، هر دنباله `(∀x_i)β` را برمی‌آورد. یعنی `⊧_M(∀x_i)β`.
ب. `⊧_M(∀x_i)β` را فرض بگیرید. اگر `s` یک دنباله باشد، آنگاه هر دنبالهای که حداکثر در مکان `i`ام با `s` متمایز باشد، `β` را برمی‌آورد، و به ویژه، `s` فرمول `β` را برخواهد آورد. یعنی `⊧_Mβ`.
VIII.
لم: اگر همه متغیرهای ترم `t` در فهرست `x_(i_۱), …,x_(i_k)` قرار گیرند (`k≥۰` - اگر `t` دارای متغیر نباشد آنگاه `k=۰`)، و اگر دنباله های `s` و `s'` در مولفه‌های `i_۱`ام تا `i_k`ام یکسان باشند آنگاه:
`s`*`(t)=(s')`*`(t)`.
اثبات لم:
با استقرا روی `m` تعداد حروف تابعی در ترم `t` اثبات را پی می‌گیریم. فرض کنید که نتیجه برای همه اعداد صحیح کمتر از `m` برقرار است.
حالت ۱. `t` ثابت انفرادی `a_p` است. بنابراین:
`s`*`(a_p)=(a_p)^M=(s')`*`(a_p)`.
حالت ۲. `t` متغیر `x_(i_j)` است. بنابراین:
`s`*`(x_(i_j)) = s_i(j) = s'_i(j) = (s')`*`(x_(i_j))`.
حالت ۳. `t` به صورت `f_i^n(t_۱,...,t_n)` است.
برای `q ≤ n`، هر `t_q` دارای کمتر از `m` حرف تابعی است و همه متغیرهای آن در میان `(x_۱,...,x_n)` قرار می گیرند. پس با توجه به فرض استقرا داریم:
`s`*`(t_q) = (s')`*`(t_q)`.
بنابراین:
`s`*`(f_j^n(t_۱,...,t_n)) =` `(f_i^n)^M (s`*`(t_1),...,s`*`(t_n))` `=`
`(f_i^n)^M (s'`*`(t_1),...,s'`*`(t_n))=` `(s')`*`(f_i^n(t_1,...,t_n))`.
اثبات VIII:
اثبات را با استقرا روی `r` تعداد رابط‌ها و سورها در `β` پی می‌گیریم. فرض کنید که نتیجه برای همه `q<r` برقرار است.
حالت ۱.
`β` به صورت `A_j^n(t_۱,...,t_n)` است، یعنی `r=۰`. همه متغیرهای هر یک `t_i` در میان `x_(i_۱),...,x_(i_k)` هستند. بنابراین، بنا بر لم اثبات شده داریم:
`s`*`(t_i)=s'`*`(t_i)`.
اما `s` فرمول `A_j^n(t_۱,...,t_n)` را برمی‌آورد اگر و فقط اگر:
`〈(s)`*`(t_۱),....,(s)`*`(t_n)〉` در `(A_j^n)^M` باشد.
یعنی، اگر و فقط اگر:
`〈(s')`*`(t_۱),....,(s')`*`(t_n)〉` در `(A_j^n)^M` باشد.
و این معادل با این است که `s'` فرمول `A_j^n(t_۱,...,t_n)` را برمی‌آورد.
حالت ۲.
`β` به صورت `¬ς` است.
حالت ۳.
`β` به صورت `ς ⇒ δ` است.
اثبات حالت‌های ۲ و ۳ هر دو آسان است.
حالت ۴.
`β` به صورت `(∀x_i)ς` است. متغیرهای آزاد `ς` در بین `x_(i_۱),...,x_(i_k)` و `x_j` وجود دارند. فرض کنید `s` فرمول `β` را برآورده کند. پس هر دنبالهای که حداکثر در مولفه `j`ام با `s` متفاوت است، `ς` را برآورده می‌کند.
فرض کنید `s^#` هر دنبالهای باشد که حداکثر در مولفه `j`ام با `s` متفاوت باشد. نیز فرض کنید `s^b` دنبالهای باشد که در همه مولفه‌ها با `s` به جز در مولفه `j`ام یکسان باشد، جایی که دارای مولفه‌های یکسان با `s^#` است. از این رو، `s^b` فرمول `ς` را برمی‌آورد. از آنجایی که `s^b` و `s^#` در مولفه‌های `i_۱`ام تا `i_k`ام و `j`ام موافق هستند، از فرض استقرا به دست می‌آید که `s^b` فرمول `ς` را برمی‌آورد اگر و فقط اگر `s^#` فرمول `ς` را برآورد. از این رو، `s^#` فرمول `ς` را برمی‌آورد. بنابراین، `s'` فرمول `β` را برآورده می‌کند. با تقارن، عکس آن نیز برقرار است.
IX.
فرض کنید فرمول `β` بسته است. از (VIII)، برای هر دنباله `s` و `s'`، دنباله `s` فرمول `β` را برمی‌آورد اگر و فقط اگر `s'` فرمول `β` را بربیاورد. بنابراین، هر دنباله `s` فرمول `β` را برمی‌آورد. یعنی `⊧_M B`.
X.
با استقرا روی `m` تعداد حروف تابعی در ترم `t` اثبات را پی می‌گیریم.
حالت ۱. `t` از قرار `a_j` است. بنابراین `t'` عبارت است از `a_j`. از اینجا:
`s`*`(t')=s'`*`(a_j)=(a_j)^M = (s')`*`(a_j)=`
`(s')`*`(t)`.
حالت ۲. `t` وقتی که `j ≠ i` عبارت است از `x_j`.
پس `t′` عبارت است از `x_j`. از اینجا، `t'` عبارت خواهد بود از `x_j`. بنابر لم (VIII)، از آنجایی که `s` و `s'` در مولفه `j`ام یکسان هستند، داریم:
`s`*`(t′) = (s′)`*`(t)`.
حالت ۳.
`t` عبارت است از `x_i`. پس `t'` عبارت است از `u`. از این رو،
`s^***(t′) = s^***(u)`.
وقتی که
`(s′)^***(t) = (s′)^***(x_i) =s′_i = s^***(u)`.
حالت ۴.
`t` به صورت `f_j^n(t_۱,...,t_n)` است. برای `۱ ≤ q ≤ n`، فرض کنید `t_q^′` نتیجه شده از `t_q` با جایگزینی `u` بجای `x_i` باشد. اما و بنابراین:
`(s)^***(t') = s^***(f_j^n(t_۱^',...,t_n^')) =`
`(f_j^n)^M(s^***(t_۱^'), ..., s^***(t_n^')) =`
`(f_j^n)^M ((s')^***(t_۱),...,(s')^***(t_n)) =`
`(s')^***(f_i^j(t_1,...,t_n)) = (s')^*** (t)`
با استقرا روی `m` تعداد رابط‌ها و سورها در `B(x_i)` اثبات را پی می‌گیریم.
حالت ۱. `m=۰`
در این حالت `β(x_i)` عبارت خواهد بود از `A_j^n (t_۱,…,t_n)`. فرض کنید `t_q^'` نتیجه جایگزینی `t` برای تمام رخدادهای `x_i` در `t_q` باشد. بنابراین، `β(t)` از قرار `A_j^n (t_۱^',…,t_n^')` خواهد بود. بنابر لم ۱ داریم `s^***(t_q^')=(s')^***(t_q)`.
اکنون، `s` فرمول `β(t)` را برمی‌آورد اگر و فقط اگر `〈s^***(t_۱^'),...,s^***(t_n^')〉` متعلق به `(A_j^n)^M` باشد، این معادل است با `〈(s')^***(t_۱),...,(s')^***(t_n)〉` متعلق به `(A_j^n)^M` است — یعنی، `s'` فرمول `B(x_i)` را برمی‌آورد.
حالت ۲. `β(x_i)` عبارت است از`¬ς(x_i)`. اثبات این حالت سر راست است.
حالت ۳. `β(x_i)` عبارت است از `ς(x_i)⇒β(x_i)`. اثبات این حالت سر راست است.
حالت ۴. `β(x_i)` عبارت است از `(∀x_i)B(x_j)`.
حالت ۴.آ: `x_j` عبارت است از `x_i`.
بنابراین، `x_i` در `β(x_i)` آزاد نیست، و `β(t)` عبارت از `β(x_i)` است. از آنجایی که `x_i` در `β(x_i)` آزاد نیست، از (VIII) به دست می‌آید که `s` فرمول `β(t)` را برمی‌آورد اگر و فقط اگر `s′` فرمول `β(x_i)` را برآورد.
حالت ۴.ب: `x_j` با `x_i` متفاوت است.
از آنجایی که `t` برای `x_i` در `β(x_i)` آزاد است، `t` برای `x_i` در `ς(x_i)` نیز آزاد است.
فرض کنید `s` فرمول `(∀x_j)ς(t)` را برآورد. ما باید نشان دهیم `s'` فرمول را `(∀x_j)ς(x_i)` را برمی‌آورد. گیریم `s^#` دنبالهای باشد که با `s′` حداکثر در مولفه `j`ام تفاوت داشته باشد. کافی است نشان دهیم که `s^#` فرمول `ς(x_i)` را برمی‌آورد.
فرض کنید `s^b` همان `s^#` باشد با این تفاوت که مولفه `i`ام یکسان با `s` را دارد. از این رو، `s^b همان `s` است به جز در مولفه `j`ام آن. از آنجایی که `s` فرمول `(∀x_j)ς(t)` را برمی‌آورد، `s^b` فرمول `ς(t)` را برخواهد آورد. اکنون، چون `t` برای `x_i` در `(∀x_j)ς(x_i)` آزاد است، ترم `t` دارای `x_j` نیست. (امکان دیگر، اینکه `x_i` در `ς(x_i)` آزاد نباشد، که مانند مورد آ.۴ رفتار خواهد شد).
از این رو، بر اساس لم (VIII) داریم:
`(s^b)^***(t) = s^***(t)`.
پس، بنا بر فرض استقرا و اینکه `s^#` از `s^b` با جایگزین کردن `(s^b)^***(t)` به جای مولفه `i`ام در `s^b` بدست می‌آید، نتیجه می‌شود که `s^#` فرمول `ς(x_i)` را برمی‌آورد، اگر و فقط اگر `s^b` فرمول `ς(t)` را برآورد. از آنجایی که `s^b` فرمول `ς(t)` را برمی‌آورد، دنباله `s^#` فرمول `ς(x_i)` را برخواهد آورد.
برعکس، فرض کنید `s'` فرمول `(∀x_j)ς(x_i)` را برمی‌آورد. گیریم `s^b` حداکثر در مولفه `j`ام با `s` متفاوت باشد. `s^#` را همان `s'` فرض کنید که به جز در مولفه `j`ام همان `s^b` است. [یعنی، `s^#` همان `s'` باشد، ولی در مولفه `j`ام با `j`امین مولفه `s^b` جایگزین شده باشد.] پس `s^#` فرمول `ς(x_i)` را برمی‌آورد و مثل بالا داریم:
`s^***(t)=(s^b)***(t)`.
بنابراین، بنا بر فرض استقرا، `s^b` فرمول `ς(t)` را برمی‌آورد اگر و فقط اگر `s^#` فرمول `ς(x_i)` را بربیاورد. از آنجایی که `s^#` فرمول `ς(x_i)` را برآورده می‌کند، `s^b` نیز فرمول `ς(t)` را برمی‌آورد. بنابراین، `s` فرمول `(∀x_j)ς(t)` را برخواهد آورد.
فرض کنید `s` فرمول `(∀x_i)β(x_i)` را برمی‌آورد. باید نشان دهیم که `s` فرمول `β(t)` را نیز برمی‌آورد. گیریم `s'` از `s` با جایگزینی `s^***(t)` به جای `i`امین مولفه `s` ناشی شده باشد. از آنجایی که `s` فرمول `(∀x_i)β(x_i)` را برمی‌آورد و `s'` با `s` حداکثر در جای `i`ام متفاوت است،`s'` فرمول `β(x_i)` را برمی‌آورد. از لم آ.۲ داریم، `s` فرمول `β(t)` را برخواهد آورد.
۲.۱۳ ثابت کنید فرمول بسته `β` برای `M` درست است اگر و فقط اگر `β` با برخی دنباله `s` در Σ برآورده شود. (به یاد داشته باشید که Σ مجموعه دنباله‌های نامتناهی-شمارا عناصر در دامنه `M` است.
حل:
فرض کنید `β` با دنباله `s` برآورده شود. فرض کنید `s'` یک دنباله (هر دنبالهای) باشد. از (VIII) بدست می‌آید که `s'` نیز `β` را برمی‌آورد. یعنی `⊧_M β`.
۲.۱۴ ویژگی‌ها یا رابطه‌های تعیین شده توسط فرمول‌ها و تعبیرهای زیر را بیابید.
a:
`[(∃u)A_۱^۲ (f_۱^۲(x ,u), y)]` `∧` `[(∃v) A_۱^۲(f_۱^۲(x,v),z)]`
که در آن دامنه `D` مجموعه اعداد صحیح است، `A_۱^۲` تساوی (=) و `f_۱^۲` ضرب است.
ح. `x` مقسوم علیه مشترک `y` و `z` است.
b: در زیر (ii ,i) دامنه `D` مجموعه اعداد صحیح غیر منفی است، `A_۱^۲` تساوی (=)، `f_۱^۲` جمع و `f_۲^۲` ضرب است و `a_۱` به ۰ دلالت می‌کند.
i: `[(∃z)(¬A_۱^۲(z, a_۱)` `∧` `A_۱^۲(f_۱^۲(x, z), y))]`
ii: `(∃y)(A_۱^۲(x, f_۲^۲(y, y))`
c: در زیر دامنه `D` مجموعه اعداد صحیح مثبت است، `A_۱^۲` تساوی (=)، `f_۱^۲` ضرب است.
`(∃x_۳)A_۱^۲(f_۱^۲(x_۱, x_۳), x_۲)`
d: در زیر دامنه `D` مجموعه همه انسان‌های زنده است، `A_۱^۱(x)` به معنای `x` یک مرد است و `A_۱^۲(x,y)` به معنی `x` با `y` ازدواج کرده است.
`A_۱^۱(x_۱) ∧(∀x_۲)¬A_۱^۲(x_۱, x_۲)`
e: در زیر (ii ,i) دامنه `D` مجموعه همه انسانها است، `A_۱^۲(x,y)` به معنای `x` پدر یا مادر y است و `A_۲^۲(x,y)` به معنی `x` و `y` خواهر برادر (یا برادر خواهر) هستند.
i. `(∃x_۱)(∃x_۲)(A_۱^۲(x_۱, x_۳)` `∧` `A_۱^۲(x_۲, x_۴)∧A_۲^۲(x_۱, x_۲))`
ii. `(∃x_۳)(A_۱^۲(x_۱, x_۳)` `∧` `A_۱^۲(x_۳, x_۲))`
f: در زیر دامنه `D` مجموعه اعداد صحیح مثبت است، `A_۱^۲` تساوی (=)، `f_۱^۲` ضرب است و `a_۱ به ۱ دلالت می‌کند.
`(∀x_۳)((∃x_4)A_1^2(f_1^2(x_4,x_3), x_1)` `∧` `(∃x_4)(A_1^2(f_1^2(x_4,x_3), x_2))` `⇒` `A_1^2(x_3, a_1))`
g: در دامنه `D` مجموعه همه انسانها است، `A_۱^۲(u, v)` به معنای `u` پدر یا مادر `v` است و `A_۲^۲(u,v)` به معنی `u` همسر (زن) `v` است.
`¬A_۱^2(x_2,x_۱)` `∧` `(∃y)(A_۱^2(y,x_۱)` `∧` `A_2^2(x_2, y))`
۲.۱۵ برای هر یک از جملات و تعبیرهای زیر یک برگردان به فارسی معمول بنویسید و درستی یا نادرستی آن را مشخص کنید.
a. `D` مجموعه اعداد صحیح غیرمنفی است، `A_1^2` تساوی (=)، `f_1^2` جمع و `f_2^2` ضرب است. `a_1` به ۰ و `a_2` به ۱ دلالت می‌کند.
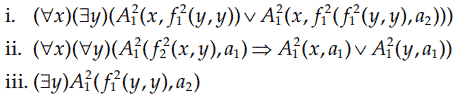
حل:
i. هر عداد صحیح غیرمنفی زوج یا فرد است. (درست).
ii. اگر حاصل ضرب دو عدد صحیح غیرمنفی صفر باشد، حداقل یکی از آنها صفر است. (درست).
iii. عدد ۱ زوج است. (نادرست).
b. که: `D` مجموعه اعداد صحیح است، `A_۱^۲` تساوی (=)، `f_۱^۲` جمع است.
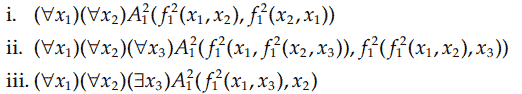
c. تمرین b، اما `D` مجموعه اعداد صحیح مثبت است، `A_1^2` تساوی (=)، `f_1^2` عبارت از `x^y` است.
d. که `D` مجموعه اعداد گویا است، `A_1^2` تساوی (=)، `A_2^2` کوچکتر (>)، `f_1^2` ضرب و `f_1^1` عبارت از `x+1` است.
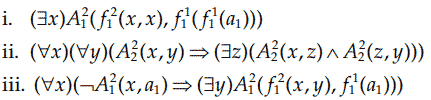
e. که `D` مجموعه اعداد صحیح غیرمنفی است، `A_1^2(u,v)` به معنی `u<v`، `A_1^3(u,v,w)` به معنی `u+v=w` است.
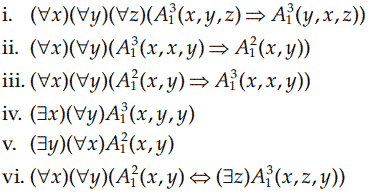
f. که: `D` مجموعه اعداد صحیح غیرمنفی است، `A_۱^۲(u,v)` تساوی (=)، `f_۱^۲` جمع و `f_۲^۲` ضرب است.
`(∀x)(∃y)(∃z)` `A_1^2(x, f_1^2(f_2^2(y,y), f_2^2(z,z)))`
■ انگاشت‌های «منطقاً معتبر»، «استلزام منطقی» و «نتیجه منطقی»
منطقاً معتبر
می‌گوییم فرمول `β` منطقاً معتبر است اگر و تنها اگر `β` برای هر تعبیر درست باشد*. (به عبارت دیگر، `β` منطقاً معتبر است اگر و تنها اگر هر تعبیر مدل `β` باشد).
[*- ریاضیدان فیلسوف لایب‌نیتس تعریفی مشابه ارائه کرد: `β` منطقاً معتبر است اگر و تنها اگر `β` برای هر جهان ممكن درست باشد].
یکی از اصول کلیدی در فلسفه لایب‌نیتس، اصل دلیل کافی↝ است که معتقد است هیچ رویداد بدون دلیل نیست. در زمینه استدلال‌های منطقی، این اصل دلالت دارد که یک نتیجه‌گیری معتبر باید لزوماً از مقدمات حاصل شود - اگر مقدمات درست باشد، باید دلیل کافی برای درست بودن نتیجه وجود داشته باشد. از اصول دیگر در فلسفه لایب نیتس، اصل جایگزینی و یکسانی شناسا ناپذیرها↝ (Substitutivity and Identity of Indiscernibles) است. این اصل مبنایی برای منطق صوری و درک اعتبار منطقی است. این اصل امکان جایگزینی عبارات با معانی یکسان را بدون تأثیر بر صدق یک گزاره فراهم می‌کند.↧Timothy Williamson ‘Is logic the study of validity?’ in Elke Brendel, Massimiliano Carrara, Filippo Ferrari, Ole Hjortland, Gil Sagi, Gila Sher, and Florian Steinberger (eds.), The Oxford Handbook of the Philosophy of Logic. Oxford: Oxford University Press.
صدق‌پذیر (برآوردنی - Satisfiable)
فرمول β را صدق‌پذیر (برآوردنی - Satisfiable) می‌گوییم اگر و تنها اگر تعبیری وجود داشته باشد که تحت آن تعبیر حداقل یک دنباله β را برآورد. (به عبارت دیگر، گفته می‌شود فرمول β صدق‌پذیر است اگر و تنها اگر تعبیری وجود داشته باشد که آن تعبیر مدل β باشد.)
بدیهی است که β منطقاً معتبر است اگر و فقط ¬β صدق‌پذیر نباشد [به عبارت دیگر، β صدق‌پذیر است اگر و تنها اگر ¬β منطقاً معتبر نباشد.
فرمول بسته و صدق‌پذیری
اگر β یک فرمول بسته باشد، می‌دانیم که β برای هر تعیبر درست یا نادرست است. یعنی همه دنباله‌ها β را برمی‌آورند یا با هیچ دنبالهای برآوردنی نیست. بنابراین، اگر β بسته باشد، β برآوردنی است اگر و فقط اگر β برای برخی از تعبیر درست باشد.
مجموعه فرمول صدق‌پذیر
به مجموعه فرمول Γ می‌گوییم صدق‌پذیر (برآوردنی) است اگر و فقط اگر تعبیری وجود داشته باشد که در آن دنبالهای باشد که هر فرمول در Γ را برآورد (که در هر فرمول Γ صدق کند).
استلزام منطقی
گوییم β منطقاً مستلزم ς است اگر و فقط اگر، در هر تعبیری، هر دنبالهای که β را برمی‌آورد، ς را نیز برآورد. به طور کلی‌تر، گفته می‌شود که ς نتیجه منطقی مجموعه فرمول Γ است، اگر و فقط اگر، در هر تعبیری، هر دنبالهای که همه فرمول‌های Γ را برآورد، ς را نیز برآورد کند. [به عبارت دیگر، ς نتیجه منطقی مجموعه فرمول Γ است، اگر و فقط اگر، در هر مدل Γ مدل ς نیز باشد].
هم‌ارز منطقی
گوییم که β و ς منطقاً هم‌ارز هستند اگر و تنها اگر منطقاً مستلزم یکدیگر باشند.
■ برخی احکام
احکام زیر نتیجه‌های سرراست تعاریف بالا هستند.
β منطقاً مستلزم ς است اگر و فقط اگر β ⇒ ς منطقاً معتبر باشد.
β و ς منطقاً هم‌ارز هستند اگر و فقط اگر β ⇔ ς منطقاً معتبر باشد.
اگر β منطقاً مستلزم ς باشد و β در یک تعبیر داده شده درست باشد، ς نیز درست است.
اگر ς نتیجه منطقی مجموعه فرمول Γ از باشد و همه فرمول‌های Γ در یک تعبیر داده شده درست باشند، ς نیز چنین است.
■ تمرین بیشتر و حل برخی (۲.۱۶ - ۲.۲۶)
۲.۱۶ مثال:
- ۱. هر مورد یک توتولوژی منطقاً معتبر است ( VII).
- ۲. اگر `t` برای `x` در `β(x)` آزاد باشد، آنگاه`(∀x)β(x) ⇒ β(t)` منطقاً معتبر است ( X).
- ۳. اگر `β` دارای `x` آزاد نباشد، `(∀x)(β⇒ς)` `⇒` `(β⇒(∀x)ς)` منطقا معتبر است (XI).
- ۴. `β` منطقا معتبر است اگر و فقط اگر `(∀y_۱) … (∀y_n)β` منطقا معتبر باشد (VI).
۵. فرمول
`(∀x_۲)(∃x_۱)A_۱^۲(x_۱,x_۲)` `⇒` `(∃x_۱)(∀x_۲)A_۱^۲(x_۱,x_۲)`
منطقا معتبر نیست. به عنوان مثال، دامنه `D` را مجموعه اعداد صحیح و معنای `A_۱^۲(y,z)` را `y < z` بگیرید. در این صورت `(∀x_۲)(∃x_۱)A_۱^۲(x_۱,x_۲)` درست است اما `(∃x_۱)(∀x_۲)A_۱^۲(x_۱,x_۲)` نادرست است.
۲.۱۷ نشان دهید فرمول‌های زیر منطقا معتبر نیستد.
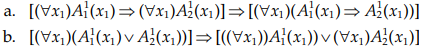
حل (a): تعبیری را در نظر بگیرید که دامنه آن مجموعه اعداد صحیح باشد. `A(x_1^1)` به معنای x زوج است و `A_2^1(x)` را به معنی x فرد است بگیرید. در این صورت `(∀x_1)A_1^1(x_1)` نادرست است و از اینجا:
`(∀x_1)A_1^1(x_1)⇒(∀x_1)A_2^1(x_1)` درست است.
ولی، `(∀x_1)(A_1^1(x_1)⇒A_2^1(x_1))` نادرست است، زیرا مدعی فرد بودن همه اعداد زوج است.
۲.۱۸ نشان دهید فرمول‌های زیر منطقا معتبر هستند.*
[*. در این مرحله، می‌توان از استدلال های شهودی استفاده کرد یا می‌توان از تعاریف دقیق رضایت و صدق، مانند استدلال بالا برای (XI) استفاده کرد. در ادامه روش دیگری برای نشان دادن اعتبار منطقی کشف خواهیم کرد.]
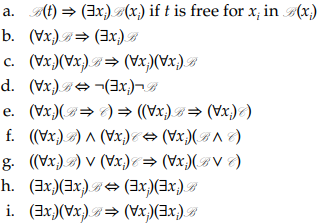
حل (a):
فرمول:
`[(∀x_i )¬β (x_i)⇒¬β(t)]⇒[β(t)⇒¬(∀x_i )¬β(x_i)]`
منطقا معتبر است زیرا موردی از توتولوژی است `(α⇒¬ β)⇒(β⇒¬α)`↱. اما از (X) می‌دانیم که فرمول `(∀x_i)¬β(x_i)⇒¬β(t)` منطقا معتبر است. بنابراین، توسط (III)، فرمول `β(t)⇒¬(∀x_i )¬β(x_i)` منطقا معتبر است.
حل (b):
اثبات شهودی: اگر `β` برای هر `x_i` درست باشد، `β` برای برخی `x_i` نیز درست است (توجه داشته باشید که دامنه تعبیر تهی نیست).
اثبات دقیق: فرض کنید `(∀x_i)β⇒(∃_i)β` منطقا معتبر نیست. پس تعبیر `M` وجود دارد که این فرمول برای آن درست نیست. از این رو، دنبالهای مانند `s` در Σ هست به قسمی که `s` فرمول `(∀x_i)β` را برمی‌آورد و `s` فرمول `¬(∀x_i)¬β`↝ را برنمیآورد. از این داریم، دنباله `s` فرمول `(∀x_i)¬β` را برمی‌آورد. اما `s` فرمول `(∀x_i)β` را برمی‌آورد، پس `β` را نیز برخواهد آورد، و چون این `s` فرمول `(∀x_i)¬β` را برآورده است، `s` فرمول `¬β` را هم برمی‌آورد. پس `s` هم `β` و هم `¬β` را برخواهد آورد، که این ممکن نیست.
۲.۱۹
a. اگر `β` یک فرمول بسته باشد، نشان دهید `β` منطقا دلالت بر `ς` دارد اگر و فقط اگر `ς` برای هر تعبیری که `β` برای آن درست است نیز باشد.
b. اگرچه، با (VI)، فرمول `(∀x_1)A_1^1(x_1)` هر گاه که `A_1^1(x_1)` درست باشد، درست است، تعبیری را بیابید که `A_1^1(x_1)⇒(∀x_1)A_1^1(x_1)` برای آن درست نباشد. (از این رو، این فرض بسته بودن `β` در (a) ضروری است).
حل b. دامنه تعبیر را مجموعه اعداد صحیح در نظر بگیرید و`A_1^1(u)` را به معنی زوج بودن `u` بگیرید. اکنون، دنباله `s` که در آن `s_1` زوج است، `A_1^1(x_1)` را برمی‌آورد، ولی `(∀x_1)A_1^1(x_1)` را برنخواهد آورد.
۲.۲۰
ثابت کنید که اگر متغیرهای آزاد `β` عبارت باشند از `y_1, …, y_n`، آنگاه `β` صدق‌پذیر است اگر و فقط اگر `(∃y_1)، …، (∃y_n)β` صدق‌پذیر باشد.
۲.۲۱
با آوردن مثال‌های خلاف نشان دهید فرمول‌های زیر منطقا معتبر نیستند (یعنی در هر مورد، تعبیری بیابید که فرمول برای آن درست نیست).
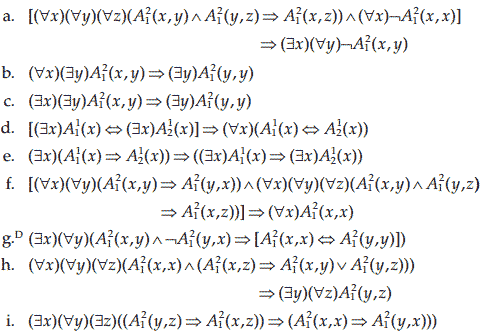
۲.۲۲
با معرفی نمادهای مناسب، جملات هر یک از استدلال‌های زیر را به صورت فرمول درآورید و مشخص کنید که آیا استدلال صحیح است یا نه، یعنی مشخص کنید که آیا نتیجه منطقا از عطف مقدمات به دست آمده است یا نه.
a. همه دانشمندان روان رنجور هستند. هیچ گیاهخواری روان رنجور نیست. بنابراین، هیچ گیاهخواری دانشمند نیست. [ صور معتبر قیاس را ببینید.]
حل a:
مقدمات عبارتند از `(i): (∀x)(S(x) ⇒ N(x))` و `(ii): (∀x)(V(x) ⇒ ¬N(x))`، و نتیجه این است `(∀x)(V(x) ⇒ ¬S(x))`.
اثبات شهودی: `V(x)` را فرض بگیرید. توسط (ii)، `¬N(x)`. توسط (i)، `¬S(x)`. بنابراین، `¬S(x)` از `V(x)` به دست می آید، و نتیجه گیری درست است. برهان دقیق‌تر را می‌توان در راستای (I) - (XI) ارائه کرد. [در یادداشت‌های بعدی، نظریه حساب محمولات، برهان دقیق را در دسترس خواهیم داشت].
b. همه مردها حیوان هستند. برخی از حیوانات گوشتخوار هستند. بنابراین، برخی از مردان گوشتخوار هستند. [ صور معتبر قیاس را ببینید.]
c. برخی از نوابغ مجرد هستند. برخی از دانش آموزان مجرد نیستند. بنابراین، برخی از دانش آموزان نابغه نیستند. [ صور معتبر قیاس را ببینید.]
d. هر آرایشگر در جونزویل (Jonesville) دقیقاً مردانی را در جونزویل اصلاح می‌کند که خودشان را اصلاح نمی‌کنند. از این رو، در جونزویل هیچ آرایشگری وجود ندارد.
e. برای هر عدد `x, y, z`، اگر `x > y` و `y > z`، آنگاه `x > z`. برای هر `x` رابطه `x>x` نادرست است. بنابراین، برای هر عدد `x` و `y` ، اگر `x > y` باشد، چنین نیست که `y > x`.
f. هیچ دانشجویی در کلاس آمار باهوش تر از دانشجویان کلاس منطق نیست. از این رو، برخی از دانشجویان در کلاس منطق باهوش تر از هر دانشجو در کلاس آمار هستند. [ صور معتبر قیاس را ببینید.]
g. همه افراد عاقل می‌توانند ریاضیات را بفهمند. هیچ یک از پسران هگل نمی‌توانند ریاضیات را بفهمند. هیچ دیوانه‌ای شایسته رای دادن نیست. از این رو، هیچ یک از پسران هگل شایسته رای دادن نیستند. [ صور معتبر قیاس را ببینید.]
h. یرای هر مجموعه `x`، یک مجموعه `y` وجود دارد به قسمی که کاردینال `y` از کاردینال `x` بزرگتر است. اگر `x` در `y` گنجانده شود، کاردینال `x` از کاردینال `y` بزرگتر نیست. همه مجموعه‌ها در `V` گنجانده شده‌اند. بنابراین، `V` مجموعه نیست.↝
i. برای هر عدد صحیح مثبت `x` داریم `x ≤ x`. برای هر عدد صحیح مثبت `x، y، z`، اگر `x ≤ y` و `y ≤ z`، آنگاه `x ≤ z`. برای هر عدد صحیح مثبت `x` و `y`، `x ≤ y` یا `y ≤ x`. بنابراین، عدد صحیح مثبت `y` وجود دارد به قسمی که، برای هر عدد صحیح مثبت `x` داریم `y ≤ x`.
j. برای هر عدد صحیح `x, y, z`، اگر `x > y` و `y > z` ، آنگاه `x > z`. `x > x` برای هر عدد صحیح `x` نادرست است. بنابراین، برای هر عدد صحیح `x` و `y`، اگر `x > y` باشد، چنین نیست که `y > x` .
۲.۲۳
تعیین کنید که آیا مجموعه‌های فرمول زیر سازگار هستند یا خیر - یعنی، آیا عطف آنها صدق‌پذیر است یا نه.
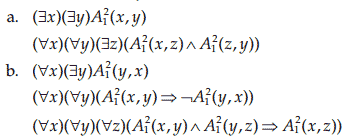
c. همه تک شاخ‌ها حیوان هستند. هیچ تک شاخ حیوان نیست.
۲.۲۴
تعیین کنید که آی فرمول‌های زیر منطقا معتیر هسنتد.
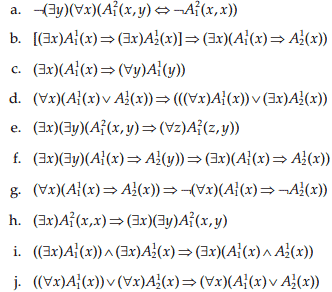
c. همه تک شاخ ها حیوان هستند. هیچ تک شاخ حیوان نیست.
۲.۲۵
یک فرمول منطقا معتبر را مثال بزنید که موردی از توتولوژی نیست. با این حال، نشان دهید که هر فرمول باز (یعنی یک فرمول بدون سور) منطقا معتبر باید موردی از یک توتولوژی باشد.
۲.۲۶
a. یک فرمول بسته صدق‌پذیر بیابید که در هر تعبیری که دامنه آن فقط یک عضو داشته باشد درست نباشد.
حل a: `(∃x)(∃y)(A_۱^۱(x) ∧ ¬A_۱^۱(y))`
b. یک فرمول بسته صدق‌پذیر بیابید که در هر تعبیری که دامنه آن کمتر از سه عضو داشته باشد درست نباشد.
