≡
فهرست:
نظریه رایانش - قضیه بازگشت درآمدی یه منطق

قضیه رایس، رتبه بندی مسائل حل نشدنی و قضیه بازگشت

منطق و نظریه رایانش (۶)

درآمد به منطق

در قسمت پیشین نظریه رایانش، ابتدا مسئله‌های نیمی-حل‌شدنی (نیمی-تصمیم‌پذیر) مورد بررسی قرار گرفت. در ادامه آن نمونه‌های مشهوری از مسئله‌های حل نشدنی را دیدیم و دو روش برای اثبات حل ناشدنی آن‌ها از قرار روش قطری و روش کاهش معرفی گردید.

در این قسمت:
آ- ابتدا به «قضیه رایس - Rice's theorem» در نظریه رایانش و پیش درآمد آن یعنی «قضیه پارامتر» می‌پردازیم. این قضیه نامدار، یعنی قضیه رایس، به گونه‌ای تکلیف حل نشدنی‌ها را یکسره خواهد کرد. این قضیه می‌گوید «هر مسئله تصمیم‌ گیری که دارای ویژگی نابدیهی است حل شدنی نیست».

ب- سپس با تکیه بر قضیه رایس، هم‌ارزی نگاشتی و درجه نگاشتی، سلسله مراتبی از مسئله‌های حل نشدنی که به «سلسله مراتب حسابی» معروف است را مرور خواهیم کرد و خواهیم دید که اگرچه همه حل ناشدنی‌ها حل نشدنی هستند، اما بعضی بیشتر حل نشدنی هستند.

ج- سرآخر به قضیه بسیار نامدار یعنی «قضیه بازگشت (Recursion Theorem)» می‌رسیم که به عنوان قضیه بنیادی نظریه رایانش نیز شناخته می‌شود. این قضیه می‌گوید برای هر مدل رایانشی (برنامه، ماشین‌ اندوختگانی، ماشین‌های تورینگ و مانند آن‌ها) ممکن است که خود را تکثیر کند، کاری که ویروس‌ها از همان اول می‌کردند.

روند منطق و نظریه رایانش (۶): قضیه رایس، رتبه بندی مسائل حل نشدنی و قضیه بازگشت

سلسله مراتب (پایگان) تصمیم‌ناپذیری
Bing AI. (2023). Personal communication. شکل. ۱.

≡

۱- قضیه پارامتر (نیز مشهور به قضیه s-m-n)

۵- کلاس حسابی

۲- قضیه رایس (Henry Gordon Rice)

۶- مجموعه حسابی

۳- سلسله مراتب (پایگان) حسابی (Arithmetical Hierarchy) و رتبه‌بندی مسئله‌های تصمیم‌ناپذیر

۷- قضیه بازگشت (The Recursion Theorem)

۴- سلسله مراتب (پایگان) حسابی (Arithmetical Hierarchy)

۸- منابع و ارجاعات

■ یادآور

☚: در این قسمت، همه نگاشت‌ها [توابع (کامل) و توابع جزئی]، مگر خلاف آن گفته شده باشد، از مجموعه توانی اعداد طبیعی، یعنی ℕn برای n≥۱، در ℕ تعریف می‌شوند. برای مثال:

f۱ : ℕ۲ → ℕ: f(x۱, x۲) = ۲x۱ + x۲ + ۱.

و به طور کلی:

f(x) : ℕn → ℕ.

☚: مراد از x (یا x<..,k>) دنباله متغیرهای (x۱,...,xk) برای k≥۱ است. برای مثال دنباله متغیرهای (x۱,x۲,x۳).

☚: فرض کنید A و R به ترتیب کلاس و رابطه باشند. ~A و ~R (همچنین A و R) به ترتیب عبارت‌اند از:

~A = A ⇔ {x|x ∉ A} (کلاس متمم)

~R = R ⇔ ~R(x)

• معرفی نماد ≃:

گیریم f و g دو تابع باشند. می‌نویسیم:

f ≃ g

اگر برای هر x داشته باشیم f و g هر دو معین با مقدار مساوی باشند یا هر دو معین نباشند. به عبارت دیگر:

g(x) ≃ f(x)↓ ⇔ (f (x)↑ ∧ g(x)↑) ⋁ ∃z(f (x) = z ∧ g(x) = z).

نیز گیریم Q و R رابطه‌های nتایی باشند. گوییم:

R ≃ Q

اگر برای هر x رابطه‌های R و Q هردو رایانش‌پذیر باشند یا هردو رایانش‌پذیر نباشند.

■ قضیه پارامتر (نیز مشهور به قضیه s-m-n)

قضیه مشهور به قضیه پارامتر (نیز نامیده به قضیه s-m-n، که علت نامگذاری آن را در ادامه خواهیم دید) دارای نقش بنیادی در نظریه رایانش (بیشتر در اثبات رایانش‌ناپذیری) است. این قضیه را ابتدا برای توابع دو متغیری و سپس در حالت کلی ارائه و بررسی می‌کنیم.

• قضیه پارامتر (حالت دو متغیری)

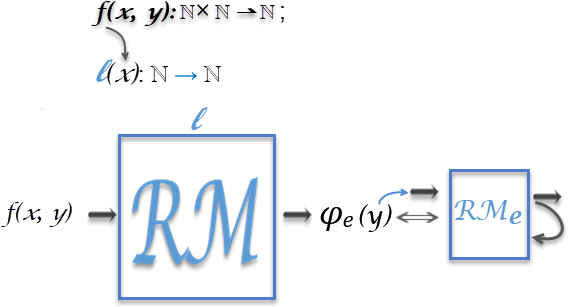
فرض کنید f(x, y) یک تابع بازگشتی جزئی (μrc) باشد. اگر در تابع f متغیر x را a به عنوان پارامتر در نظر بگیریم آنگاه↝ تابع یک متغیری ga(y) را ،که نیز μrc است، خواهیم داشت، به قسمی که: 

f(a, y) ≃ ga(y).

از آنجا که ga(y) بازگشتی جزئی است و نیز 𝓒μrc↝ برشمردنی است پس اندیس e وجود دارد به قسمی که:

f(a, y) ≃ φe(y).

قضیه پارامتر می‌گوید تابع رایانش‌پذیر l(x) وجود دارد که e را به دست می‌دهد. به عبارت دیگر، تابع رایانش‌پذیر l(x) هست به قسمی‌ که:

f(x, y) ≃ φ l(x)(y).

قضیه پارامتر - منطق و نظریه رایانش
شکل. ۱.

پیش از معرفی حالت کلی این قضیه، با ارائه مثالی با چگونگی کاربرد آن در اثبات تصمیم‌ناپذیری (مسسله‌های حل‌ناپذیر) آشنا می‌شویم.

■ مجموعه C۰ = {i:∀x φi (x) = ۰} تصمیم‌پذیر نیست.

• اثبات:

با استفاده از روش کاهش و کارزدن قضیه پارامتر نشان می‌دهیم:

K ≤m C۰

تابع دو متغیری f را مطابق زیر تعریف می‌کنیم:

f(x, y) =
۰اگر x ∈ K:
↑اگر x ∉ K:

f یک تابع μrc است. پس بنا به قضیه پارامتر↝ می‌نویسیم:

∀x, yf(x, y) = φg(x)(y),

که در آن g رایانش‌پذیر است. در این صورت:

x∈K ⇒ ∀yφg(x)(y) = C۰(y) ⟹ g(x) ∈ C۰.

x∉K ⇒ ∀yφg(x)(y)↑ ⟹ g(x) ∉ C۰.

بنابراین: تابع g مجموعه تصمیم‌ناپذیر K را به C۰ می‌کاهد↝، یعنی داریم K≤mC۰. پس C۰ تصمیم‌پذیر نیست. و می‌توان گفت درجه تصمیم‌ناپذیری K بیشتر از درجه C۰ نیست. [⇜ وارون آن، یعنی C۰≤mK برقرار نیست.]

• قضیه پارامتر (حالت کلی)

فرض کنید x = (x۱,...,xm) و y = (y۱,...,yn) باشد. نیز، تابع m+n متغیری φe(x, y) یک تابع μrc باشد. در این صورت تابع بازگشتی-نخستینی m+۱ متغیری s وجود دارد به قسمی که:

φe(x, y) ≃ φs(e, x)(y).

رابطه بالا معمولاً به صورت زیر نوشته می‌شود که علت نام‌گذاری این قضیه به s-m-n در آن آشکار است:

قضیه s-m-n در نظریه رایانش

درواقع، قضیه s-m-n رایانش‌پذیری یک تابع m+n متغیری μrc را به رایانش‌پذیری یک تابع n متغیری μrc برمی‌گرداند. اهمیت این قضیه بیشتر در اثبان دو قضیه بنیادی (قضیه رایس و قضیه بازگشت) در نظریه رایانش (عمدتاً در اثبات رایانش‌‌ناپذیری) است که در ادامه خواهیم دید است.

■ قضیه رایس (Henry Gordon Rice)

•. قضیه رایس (ویرایش یکم):

فرض کنید B یک مجموعه باشد و داشته باشیم:

 B ⊂ 𝓒۱ ∧ B ≠ ∅.

در این صورت مسئله φx∈B تصمیم‌پذیر نیست↧.

1- Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, 1980. P.105.
2- Harry R. Lewis, . Christos H. Papadimitriou. Elements of The Theory Of Computation, Prentice-Hall, 1998.

•. قضیه رایس (ویرایش دوم - ۱۹۵۳):

گیریم I یک مجموعه نمایه نابدیهی باشد، آنگاه I تصمیم‌پذیر نیست.

•. اثبات:

فرض می‌کنیم φx یک تابع μrc و B یک مجموعه نمایه (B⊂𝓒۱∧B≠∅) باشد. آنگاه داریم:

φx∈B تصمیم‌پذیر است ⟺ φx ∈ 𝓒۱ / B تصمیم‌پذیر است↝.

اکنون فرض کنید udf∅↝ متعلق به B باشد. [اگر udf∅ متعلق به B نباشد، udf∅ را متعلق به 𝓒۱/B گرفته و برهان را ادامه می‌دهیم.]

تابع g متعلق به B را انتخاب↝ و تابع f∈(x,y) را مطابق زیر تعریف می‌کنیم.

f(x, y) =
g(y)اگر x ∈ Wx:
↑اگر x ∉ Wx:

بنا به قضیه پارامتر تابع رایانش‌پذیر l(x) هست به قسمی که:

f(x, y) ≃ φl(x)(y).

بنابراین می‌توان نوشت:

x ∈ Wx↜ ⇒ φl(x) = g ⇒ φl(x) ∈ B

x ∉ Wx ⇒ φl(x) = udf∅ ⇒ φl(x) ∉ B

بنا به آنچه تا اینجا گذشت داریم:

x ∈ Wx ≤m φx∈B↜.

اما K = Wx = {n:φn(x)↓}

و می‌دانیم K تصمیم‌پذیر نیست↝. پس بنا به روش کاهش در اثبات رایانش‌ناپذیری↝، مسئله φx∈B تصمیم‌پذیر نیست.

نتیجه ۱:

با توجه به آنچه در برهان آمده است می‌توان نوشت:

K ≤m {φx∈B}.

به عبارت دیگر:

K ≤m B.

یعنی، اگر B تصمیم‌پذیر باشد آنگاه یک روند کارآمد می‌تواند به تصمیم‌پذیری K برسد. به عبارت دیگر، برای تصمیم پذیری عضویت x در K، ابتدا lx را رایانش کرده و سپس عضویت حاصل، یعنی خروجی را در B می‌آزماییم.

نتیجه ۲:

همچنین می‌توان نوشت↝:

B ≤m K.

نتیجه ۳:

از ۱ و ۲ داریم↝:

B ≡m K.

از انجاکه رابطه ≡m یک رابطه هم‌ارزی است، این رابطه کلاس مسئله تصمیم‌پذیری را به کلاس‌های هم‌ارزی افراز می‌کند. بنابراین می‌توان K را نماینده کلاس هم‌ارزی [K] گرفت و گفت تصمیم‌پذیری هیچ مجموعه رایانش‌پذیر برشمردنی سخت‌تر (سختی نسبی) از K نیست. از آنجاکه:

K۰ ≡m K↜ ⇒↜ [K] = [K۰]

می‌توانستیم K۰ را نماینده این کلاس هم‌ارزی بگیریم ولی در نظریه رایانش چنین نقشی را به K داده‌اند.

نتیجه ۴:

مجموعه‌های زیر که آشکارا مجموعه نمایه‌های نابدیهی  هستند تصمیم‌پذیر نیستند.

C۰↜ = {i: ∀n φi(n) = ۰} =
= {i: ∀x∃y T(i, x, y)↜ و φi(x) = ۰}

TOT↜ = {i: ∀n φi(n)↓} = {i: ∀x∃y T(i, x, y)}↜
= {x: Wx↜ = ℕ}

Fin = {Wi متناهی است}↜ =
= {e: متناهی است ϕe(x)} =
= {e: ∃x∀y  (y ≤ x ∨ ϕe(x) = ϕe(y)) }.

■ سلسله مراتب (پایگان) حسابی (Arithmetical Hierarchy) و رتبه‌بندی مسئله‌های تصمیم‌ناپذیر

• پایگان (سلسله مراتب - Hierarchies) سامانه‌ای است که از سازماندهی چیزها در لایه‌های مختلف بسته به درجه اهمیت آنها (در زمینه مورد مورد نظر) ناشی شده است.

مقدمه:

[پیش از ادامه این بند مناسب است نگاهی به «سلسله ‌مراتب تجمعی مجموعه‌ها (جهان فون نویمان)» در «یادآور نظریه مجموعه‌ها» داشته باشید.]

سلسله مراتب (پایگان) تصمیم‌ناپذیری

سلسله مراتب (پایگان) حسابی (Arithmetical Hierarchy) در پی ارتباط رایانش‌ (پذیری) و تعریف (‌پذیری) در منطق، رسیدن و نگریستن به قضیه‌های ناتمامیت گودل (بطور ویژه قضیه اول) و دستیابی به گونه‌ای رتبه‌بندی مسئله‌های حل نشدنی توسط رابطه ≤m است. تمرکز ما در این قسمت عمدتاً رتبه‌بندی مورد اشاره است. آنچه باقی می‌ماند در گسترش منطق محمولات مورد بحث قرار خواهد گرفت، که فعلاً مقدمات آن را می‌توان در «فصل ۱۱ - منطق محمولات» در «کتاب درآمد به منطق» یافت.

■ سلسله مراتب (پایگان) حسابی (Arithmetical Hierarchy)

تعریف. کلاس Σ۱.

فرض کنید R رابطه تصمیم‌پذیر نیز A مجموعه‌ای به قرار زیر باشد:

A = {n ∈ ℕ: ∃yR(n, y)}.

در این صورت، کلاس مجموعه‌های از گونه A را Σ۱ می‌نامیم. بنابراین، می‌نویسیم:

Σ۱ ↔ {Y: Y = {n ∈ ℕ: ∃yR(n, y) ∧ R_ تصمیم‌پذیر}}.

با توجه به تعریف Σ۱، رابطه R یک رابطه رایانش‌پذیر است پس ماشین‌ اندوختگانی (یا ماشین تورینگ) i وجود دارد که R را برای ورودی x حداکثر در s گام بر‌می‌آورد. بنابراین، Σ۱ دربردار همه مسئله‌های تصمیم‌‌گیری است که به گونه زیر بیان شدنی هستند:

{x: ∃yR(x, y) ∧ R_ r.c} ⟺ {i: ∃sT(i, x, s)↜}.

یا به گونه دیگر↝، Σ۱ کلاس مجموعه‌های c.e است.

از آنجاکه:

K = {i: ∃sT(i, i, s)↜},

بنابراین K ∈ Σ۱.

اگر کلاس مجموعه‌های رایانش‌پذیر را Cr.c بنامیم، از آنجا که هر مجموعه رایانش‌پذیر نیز مجموعه رایانش‌پذیر برشمردنی است↝، پس داریم:

Cr.c ⊂ Σ۱

تعریف: کلاس Π۱.

تعریف. مجموعه نمایه متمم (Co-c.e):

گیریم B رایانش‌پذیر برشمارشی (c.e) باشد. به متمم B، یعنی B، مجموعه نمایه متمم (Co-c.e) گفته می‌شود.

فرض کنید R رابطه تصمیم‌پذیر نیز B مجموعه‌ای به قرار زیر باشد:

B= {n ∈ ℕ: ∀yR(n, y)}.

در این صورت کلاس مجموعه‌های از گونه B را Π۱ می‌نامیم. بنابراین، می‌نویسیم:

Π۱ ↔ {Y: Y = {n ∈ ℕ: ∀yR(n, y) ∧ R_ تصمیم‌پذیر}}.

با توجه به تعریف Π۱ رابطه R یک رابطه رایانش‌پذیر است پس ماشین اندوختگانی (یا ماشین تورینگ) i وجود دارد که R را برای ورودی x حداکثر در s گام بر‌می‌آورد. بنابراین، Π۱ دریردار همه مسئله‌های تصمیم‌‌گیری است که به گونه زیر بیان شدنی هستند:

{x: ∀yR(x, y) ∧ R_ r.c} ⟺ {i: ∀sT(i, x, s)↜}.

یا به گونه دیگر↝، Π۱ کلاس مجموعه‌های Co-c.e است.

از آنجاکه:

K =  {i: ∀y φi(y)↑},

بنابراین K ∈ Π۱.

بنا به قضیه متمم، یک مجموعه تصمیم‌پذیر است اگر و تنها اگر خود و متمم آن نیمی-تصمیم‌پذیر (c.e) باشند. بنابراین اگر X تصمیم‌پذیر باشد X نیز تصمیم‌پذیر است. و ازآنجاکه:

X = X

پس، X هم در Σ۱ و هم در Π۱ هست و از اینجا می‌نویسیم:

Σ۱ ∩ Π۱ = Δ۱,

که در آن Δ۱ اشتراک Σ۱ و Π۱ است.

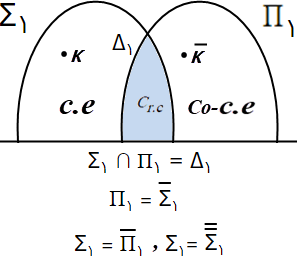
سلسله مراتب حسابی - Arithmetical Hierarchic
شکل. ۲.

⇚ از آنچه گفته شد می‌توان نوشت:

A ∈ Σ۱ ⟺ A ∈ Π۱,

A ≤m B ∧ B ∈ Σ۱ ⟹ A ∈ Σ۱.

تعریف: کلاس Σ۲.

فرض کنید R رابطه تصمیم‌پذیر نیز A مجموعه‌ای به قرار زیر باشد:

A = {n ∈ ℕ: ∃y∀sR(n, y, s)}

⟺ {n: ∃y∀sT(n, x, y, s)↜}.

در این صورت، کلاس مجموعه‌های از گونه A را Σ۲ می‌نامیم. بنابراین، می‌نویسیم:

Σ۲ ↔ {Y: Y = {n: ∃y∀sT(n, x, y, s)↜}}.

بنابراین: Fin ∈Σ۲.↝

تعریف: کلاس Π۲.

فرض کنید R رابطه تصمیم‌پذیر نیز A مجموعه‌ای به قرار زیر باشد:

B= {n ∈ ℕ: ∀y∃sR(n, s, y)}

⟺ {n: ∀y∃sT(n, x, y, s)↜}.

در این صورت کلاس مجموعه‌های از گونه B را Π۲ می‌نامیم. بنابراین، می‌نویسیم:

Π۲ ↔ {Y: Y = {n ∈ ℕ: ∀y∃sR۲(n, s, y) ∧ R_ تصمیم‌پذیر}}.

بنا بر تعریف TOT، یعنی مجموعه نمایه توابع کامل، داریم:

TOT ∈ Π۲.

نیز داریم:

TOT = {i : ∀s∃tT(i, x, t, s)↜}.
TOT= ~{i :∀s∃tT(i, x, t, y)}  
 = {i :~∀s∃tT(i, x, t, y)}  
= {i :~~∃s~∃tT(i, x, t, s)}∃xP(x) ↔ ~∀y~P(x) ↜
= {i :∃s~~∀t~T(i, x, t, s)}∀xP(x) ↔ ~∃y~P(x) ↜
= {i :∃s∀t~T(i, x, t, y)}  
= {i :∃s∀tT(i, x, t, s)}بنا به قضیه متمم، از
آنجا که T تصمیم‌پذیر
است پس T نیز
تصمیم‌پذیر است.
یعنی، TOT در Σ۲ است.

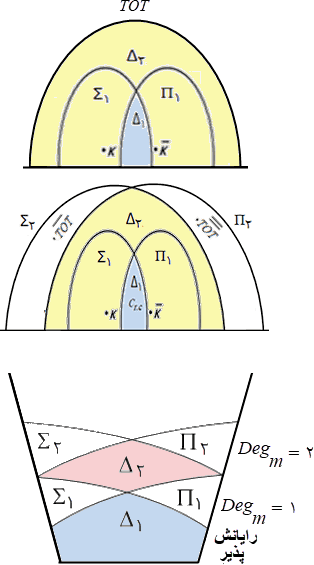
نیز با توجه به تعریف Σ۱, Σ۲, Π۱, Π۲, Δ۱, Δ۲ و اینکه هیچ یک از آنها تهی نیستند و نیز داریم:

TOT ∉ Σ۱, TOT ∉ Π۱,

همچنین، می‌توان نوشت:

Σ۱ ⊂ Σ۲, Π۱ ⊂ Π۲,

Σ۱ ⊂ Π۲, Π۱ ⊂ Σ۲,

 Δ۱ = Σ۱ ∩ Π۱, Δ۲ = Σ۲ ∩ Π۲.

A ∈ Σ۲ ⟺ A ∈ Π۲,

A ≤m B ∧ B ∈ Σ۲ ⟹ A ∈ Σ۲.

سلسله مراتب حسابی - Arithmetical Hierarchic
شکل. ۳.

به همان ترتیب که برای رتبه‌های ۱ و ۲ انجام شد، می‌توانیم فهرست نامتناهی زیر را داشته باشیم.

Σ۱ {i: ∃sT(i, x, s)↜}
Π۱ {i: ∀sT(i, x, s)↜}
Σ۲ {i: ∃y∀sT(i, x, y, s)↜}
Π۲ {i: ∀y∃sT(i, x, y, s)↜}
Σ۳ {i: ∃t∀y∃sT(i, x, y, t, s)↜}
Π۳ {i: ∀t∃y∀sT(i, x, y, t, s)↜}
.... ....

■ کلاس حسابی

تعریف:

به Σn (برای n>۰) کلاس حسابی گوییم اگر بتوان آن را به گونه زیر نوشت:

Σn>۰ = {X: X = {x: ∃y۱∀y۲. . .QynR(x, y۱, y۲, ... , yn)}},

که در آن R رابطه تصمیم‌پذیر و اگر n فرد باشد، Q سور وجودی (∃) و در غیراین صورت سور عمومی (∀) است.

به Πn (برای n>۰) کلاس حسابی گوییم اگر بتوان آن را به گونه زیر نوشت:

Πn>۰ = {X: X = {x: ∀y۱∃y۲. . .QynR(x, y۱, y۲, ... , yn)}},

که در آن R رابطه تصمیم‌پذیر و اگر n فرد باشد، Q سور عمومی (∀) و در غیراین صورت سور وجودی (∃) است.

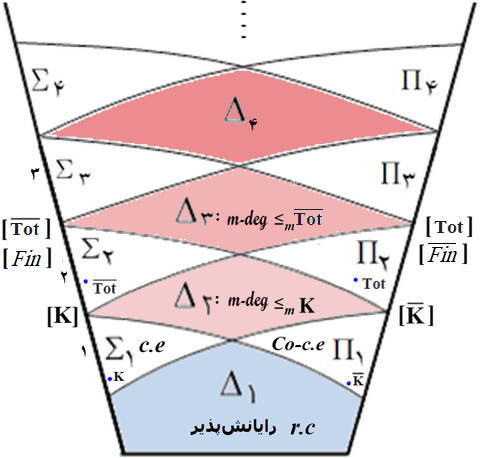
سلسله مراتب حسابی - Arithmetical Hierarchic
شکل. ۴. رتبه‌های حسابی (درجه حل‌ نشدن مسئله‌های حل نشدنی).
برای مثال، درجه حل نشدن مسئله‌های رده ۳ بیشتر از درجه حل‌ نشدن مسئله‌های رده ۲ است. (اگرچه مسئله‌های رده ۲ و ۳ همه حل نشدنی هستند، اما مسئله‌های رده ۳ بیشتر حل نشدنی هستند.)

■ مجموعه حسابی

تعریف:

به عناصر Σn و Πn مجموعه حسابی گفته می‌شود. می‌توان نشان داد:

 A ∈ Σn ⟺ A ∈ Πn.

a- Σn ⊂ Σn+۱, Σn ⊂ Πn+۱.

b- Πn ⊂ Πn+۱, Πn ⊂ Σn+۱.

c- Δn = Σn ∩ Πn.↧

Borut Robič. The Foundations of Computability Theory (Springer-Verlag Berlin Heidelberg 2015), p. 286.

d- Σ۱ ⊂ Σ۲ ⊂ Σ۲ ⊂ . . . Σn-۱ ⊂ Σn ⊂ . . ..

e- Π۱ ⊂ Π۲ ⊂ Π۲ ⊂ . . . Πn-۱ ⊂ Πn ⊂ . . ..

f- A ∈ Σn ⟹ ∀m >n; A ∈ Δm.

g- A ∈ Πn ⟹ ∀m >n; A ∈ Δm.

h- A, B ∈ Σn ⟹ A ∩ B, A ∪ B ∈ Σn.

i- A, B ∈Πn ⟹ A ∩ B, A ∪ B ∈ Πn.

j- A ≤m B ∧ B ∈ Σn ⟹ A ∈ Σn.

اگر کلاس مجموعه‌های رایانش‌پذیر را Σ. بنامیم، بنا به قضیه متمم داریم:

 Σ۰ = ‍‍~Σ۰.

بنابراین می‌نویسیم:

Σ۰ = ‍‍~Σ۰ , Π۰ ≝ ~Σ۰.

Δ۰ ≝ Σ۰ ∩ Π۰.

Σ۰ = ‍‍Π۰ = Δ۰.

☚: اگر چه ∅∈Σ۰ و ℕ∈Σ۰، اما ℕ ≰m ∅، بنابراین کلاس Σ۰ در رتبه‌بندی (ش.۵) نیامده است. به عبارت دیگر، در این رتبه درجه (نگاشتی) 0 (degm-0) یکتا وجود ندارد. در یاداشت‌های بعدی خواهیم دید که چنین درجه‌ای در رتبه‌بندی تورینگی وجود دارد.

■ قضیه بازگشت (The Recursion Theorem)

مقدمه:

ارجاع به خود - خود مرجعی (Self-reference)

کم و بیش در باره ویروس‌های کامپیوتری و اینکه آنها می‌توانند خود را تکثیر و منتقل کنند، می‌دانیم. یک ویروس‌ کامپیوتری یک برنامه کامپیوتر (یک الگوریتم / یک تابع بازگشتی / یک ماشین اندوختگانی / یک ماشین تورینگ) است. این برنامه افزون بر هدف بدخواهانه خود این توان را دارد که خود را بازآفرینی کند (از خود رونوشت بگیرد) و این رونوشت را از طریق درگاه‌های (ports) ممکن انتقال دهد. این بازآفرینی و انتقال می‌تواند همیشه ادامه یابد. برای اینکه یک برنامه بتواند خودش را بازنویسی کند باید خودش را بخواند، یعنی این برنامه باید به‌گونه‌ای به خودش ارجاع دهد (یعنی خود-مرجع↝ - Self-reference باشد)↝. این متناقض می‌نماید، اما ویروس‌های کامپیوتری این کار را انجام می‌دهند! موضوع این بند «قضیه بازگشت - Recursion theorem» در نظریه رایانش است که به موجب آن باید بتوانیم برنامه‌ای بنویسیم که بتواند خودش را کپی کند (و برای مثال آن را چاپ کند).

پیش از ادامه این بند مناسب است نگاهی به «قضیه نقطه برجا» در «یادآور نظریه مجموعه‌ها» داشته باشیم. بخشی از نمودار توضیحی آن قضیه نیز در زیر آمده است:

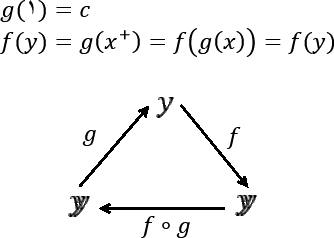
قضیه بازگشت ( نقطه برجا)در نظریه مجموعه‌ها- Fixed point theorem
شکل. ۵. قضیه نقطه برجا (Fixed point theorem)
نظریه مجموعه‌ها↝

فرض کنید f تابع رایانش‌پذیر از ℕ در ℕ و φz تابع μrc باشد. افزون بر این فرض کنید(ف-۱) n هست به قسمی که داشته باشیم:

φn(x) = φf(n)(x). :آ. فرض.۱

بنابراین، تابع μrc φf(n)(x) که در آن f(n) رایانش‌پذیر است باید وجود داشته باشد. برای رایانش این تابع باید f(n) توسط φ رایانش شود. فرض کنید مقدار f(n) برابر a شود. در این صورت بنا بر (ف-۱) باید:

تابع φ با اندیس a ≃ تابع φ با اندیس n.

از اینجا، φ باید از تعریف خودش (الگوریتم خود / کد خود) آگاه باشد تا شرط بالا برآورده کند و برای این کار باید به خودش بازگشت (رجوع) کند.

نظریه توابع بازگشتی قضیه بازگشت (Recursion theorem)
شکل. ۶. نظریه توابع بازگشتی
قضیه بازگشت (Recursion theorem)

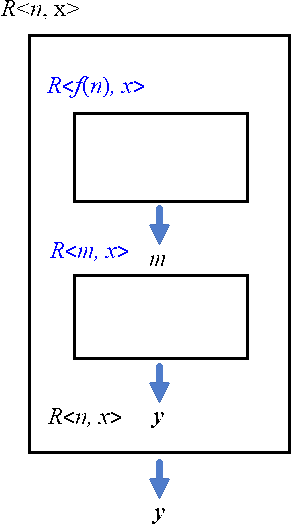
اگر جایگزین رابطه آ را برای ماشین‌های اندوختگانی بنویسیم، داریم:

R<n, x> = y = R<R<f(n), *>, *>

⇕

n ≃ R<f(n), *>.

یعنی، خروجی ماشین R ماشین R است. [در قسمت ماشین‌های تورینگ با جزئیات بیشتر به قضیه «بازگشت» باز خواهیم گشت.]↧

همچنین می‌توانید به برنامه کواین (Quine Program) در آدرس زیر مراجعه نمایید:

https://rosettacode.org/wiki/quine

قضیه بازگشت ( نقطه برجا)در نظریه مجموعه‌ها- Fixed point theorem
شکل. ۷. قضیه بازگشت

قضیه بازگشت:

گیریم f تابع رایانش‌پذیر از ℕ در ℕ و φz تابع μrc باشد؛ آنگاه n هست به قسمی که داشته باشیم:

φn = φf(n).

[n را مقدار نقطه برجا (fixed-point value) برای تابع f می‌نامند.]

اثبات:

فرض می‌کنیم d یک تابع برجا (تثبیت شده) یک‌به‌یک و f تابع دلخواه رایانش‌پذیر از ℕ در ℕ است. توجه داشته باشید که d جز آنچه گفته شد ویژگی دیگری ندارد و هنوز به‌طور کامل تعریف نشده ‌است. آشکار است که f⚬d یک تابع (کامل) است. تابع φv(x) را که در آن v مقداری برجا (تثبیت شده / fixed) است به قرار زیر در نظر می‌گیریم:

۱. φv(x) ≃ f(d(x)).

با توجه به اینکه d یک تابع معین است پس عدد n وجود دارد به قسمی که:

۲. d(v) = n.

از ۱ و ۲ داریم:

۳. φv(v) = f(d(v)) = f(n).

اکنون تابع 𝓟 در زیر را در نظر بگیرید:

𝓟(m, z) =
φφm(m)(z)اگر φm(m)↓:
↑وگرنه:

𝓟 یک تابع μrc است. از اینجا و بنا بر قضیه پارامتر تابع رایانش‌پذیر l هست به قسمی که:

۴. 𝓟(m, z) = φl(m)(z).قضیه پارامتر:

[از آنجا که تابع برجای d را تنها یک تابع رایانش‌پذیر یک‌به‌یک فرض کرده بودیم تابع l در بالا را همان d می‌گیریم.]

خلاصه آنچه تا اینجا گذشت:

۱. φv(x) ≃ f(d(x)).    
۲. d(v) = n.    
۳. φv(v) = f(d(v)) = f(n).    
۴. 𝓟(v, z) = φd(v)(z).    

اکنون می‌توانیم بنویسیم:

a.φn(z)  = φd(v)(z) از ۲:
b.𝓟(v, z)= φd(v)(z)  قضیه پارامتر:
c  = φφv(v)(z)بنا بر تعریف تابع 𝓟:
d.= φf(n)(z).از a:

منابع و ارجاعات

1- Davis, Martin, editor. The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.

2- Davis, Martin. The Universal Computer: The Road from Leibniz to Turing. CRC Press/Taylor & Francis Group, 2018.

3- Davis, Martin,  Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.

4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf

5- Stephen Cole Kleene. Mathematical logic, Dover Publications (December 18, 2002).

6- Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, (1980.)

7- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.

8- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing.  (2011).

9- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)

10- George Tourlakis, Computability, Springer International Publishing. (2022.)

11- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. (2015.)

12- Hartley Rogers, Jr· Theory of Recursive Functions and Effective Computability. The MIT Press; Fifth Printing edition (April 22, 1987).

13- Herbert B. Enderton An Introduction to Recursion Theory. Academic Press is an imprint of Elsevier (2011).

14. Dean, Walter, "Recursive Functions", The Stanford Encyclopedia of Philosophy (Winter 2021 Edition), Edward N. Zalta (ed.)

15- S. Barry Cooper. Computability theory. Chapman & Hall/CRC mathematics (2003.)

◄ توجه: