ماشین تورینگ اوراکل (غیب‌گو)
منطق و نظریه رایانش (۷)
درآمد به منطق
سقراط – (۳۹۹-۴۷۰ پیش از میلاد)
در قسمت قبل در بحث رایانش‌پذیری نسبی و روش کاهش
گفته شد که اگرچه همه مسئله‌های
حل نشدنی حل نشدنی‌اند اما برخی بیشتر↝
حل نشدنی هستند. این که برخی مسئله «حل نشدنی‌تر» است معنایی بیش از
آنچه در قسمت قبل دیدیم دارد. در این قسمت با کمک
اوراکل‌ها↧
اوراکل‌ها کاهن‌ها (نیمه فرشتگان) معبد دلفی در یونان باستان بودند که تصور می‌شد دریچه‌هایی هستند که از طریق آنها خدایان مستقیماً با مردم سخن می‌گویند.از گونه‌ای
مدل
نظری رایانش
بحث می‌کنیم که هر مورد آن به یک اوراکل مخصوص خود دسترسی دشته باشد. اوراکلِ این
ماشین، به عنوان یک موجود انتزاعی، توانایی حل یک مسئله
خاص در یک گام را دارد. افزون بر آن، ماشین می‌تواند در هر لحظه در طول اجرا
در باره هر مورد آن مسئله در یک گام از اوراکل خود پرس و جو نماید. از اینجا به
مفهوم «کاهش پذیری تورینگ»
و نیز «درجه‌ها و پرش‌های تورینگ» خواهیم رسید. در آخر با «پایگان درجه‌های تورینگ»
-- Hierarchies of Turing-Degrees -- مواجه
خواهیم شد و پایگان درجه‌های تورینگ و
پایگان حسابی
را که در قسمت قبل دیدیم باهم خواهیم دید.
ماشین تورینگ اوراکل (غیب‌گو)
■ مقدمه
☚: مراد از استعاره «اوراکل» در این قسمت، اشاره به کاهنان نیمه انسان نیمه فرشته (سروش عالم غیب↝) معبد دلفی یونان باستان است و نباید آن را با شرکت نرم‌افزاری مشهور اوراکل↝ مربوط دانست.
≡
۱- مقدمه | ۷- درجه تورینگ (Turing Degree) |
۲- اوراکل (Oracle) | ۸- پرش تورینگ (Turing Jump) |
۳- ماشین تورینگ اوراکل (Oracle Turing Machine) | ۹- سلسله مراتب (پایگان) درجه‌های تورینگ (Hierarchies of Turing-Degrees) |
۴- کاهش‌پذیری تورینگ (Turing Reducibility) | ۱۰- پایگان درجه‌های نگاشتی و پایگان درجه‌های تورینگ |
۵- مجموعه کامل تورینگ (Turing Complete) | ۱۱- منابع و ارجاعات |
۶- هم‌ارزی تورینگ (Turing Equivalence) |
در این قسمت ما به دنبال آنیم که بدانیم اگر یک مسئله غیر قابل حل
(تصمیمناپذیر)
را حل می‌کردیم، آنگاه چه رده یا رده‌های دیگر از مسئله‌های غیر قابل حل دیگر را می‌توانستیم حل کنیم.
به عبارت دیگر، می‌خواهیم روندی را برای حل مسئله‌های غیر قابل حل بیابیم!
اما «حل یک مسئله غیر قابل حل» یعنی چه؟
مدل رایانشی آن چه است؟
بنا بر تز چرج-تورینگ همه مدل‌های (ماشین‌های) رایانش هم‌ارز هستند و یک مسئله غیر قابل حل در هر مدل رایانش غیر قابل حل است. بنابراین نمی‌توان در جهان طبیعی چنین ماشینی ساخت
و یافت. اما چه می‌شود اگر یک ماشین تورینگ معمولی
(یا ماشین اندوختگانی
و مانند آن) را به
یک اوراکل↧
اوراکل (Oracle)
در اینجا اشاره به کاهن‌ها (نیمه فرشتگان) معبد دلفی در یونان باستان دارد که تصور می‌شد
دریچه‌هایی هستند که از طریق آنها خدایان مستقیماً با مردم سخن می‌گویند.
https://en.wikipedia.org/wiki/Oracle
(Oracle -
کاهن غیب گو) مجهز کنیم و آن را
ماشین
اوراکل بنامیم. یعنی، یک ماشین تورینگ معمولی که
مجهز به اوراکل مخصوص خود نیز باشد. این ماشین، یعنی ماشین اوراکل،
می‌تواند به عنوان یک دستورالعمل منفرد در خود برای پرسش از عضویت عنصری در مجموعه‌ای
مانند B از اوراکل خود پرس و جو نماید. در همین رابطه، تورینگ در پایان‌نامه دکتری خود
(که به صورت مقاله در ۱۹۳۹ توسط خود تورینگ منتشر شد) می‌نویسد:
«فرض می‌کنیم که ابزارهای نامشخصی، به عنوان یک اوراکل، برای حل
مسائل تئوری اعداد در اختیار ما قرار گرفته باشد. در اینجا ما بیشتر از این به سرشت
این اوراکل نخواهیم پرداخت، جز اینکه بگوییم این اوراکل خود نمی‌تواند یک ماشین
باشد. [اما] با کمک این اوراکل، می‌توانیم نوع جدیدی از ماشین را (که آنها را 𝒪-machines می‌نامیم)
تشکیل دهیم آنگونه که یکی از روندهای اصلی آن حل یک
مسئله تئوری اعداد معین باشد. . . ↧.»
Turing, A.M. Systems of Logic based on Ordinals. Proceedings of the London Mathematical Society 45(2), 161–228 (1939).
این مقاله را می‌توانید در کتاب زیر بیابید.
Davis, Martin, editor. The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Dover Publication, 2004.
خود تورینگ بیش از این به ماشین اوراکل نپرداخت. اما امیل پست (Emil Post) در سال ۱۹۴۴ این مفهوم را بکار گرفت↧ تا مفاهیم «کاهش‌پذیری تورینگ»، «هم‌ارزی تورینگ» و «سلسله مراتب (پایگان) درجه‌های تورینگ (Hierarchies of Turing-Degrees)» را گسترش دهد. در ادامه این قسمت آنچه گفته شد را با جزئیات مرور خواهیم کرد.
Post, E., Recursively Enumerable Sets of Positive Integers and Their Decision Problems. Bulletin of the American Mathematical Society 50, 284–316 (1944).
■ اوراکل (Oracle)
گیریم B زیرمجموعه اعداد طبیعی باشد. نیز فرض کنید بر ستیغ قله‌ای معبدی هست که در آن کاهن غیب‌گویی (Oracle) هست که بر در معبد در پس دو پیشخوان (۱ و ۲) با مدادی در دست و سر در گریبان نشسته و به پیشخوان ۱ می‌نگرد. کاهن اگر در پیشخوان ۱ نوشته‌ای بر پاره کاغذی بیابد که پرسش از عضویت عنصری در مجموعه B باشد،
برای نمونه: ،[a ∈ ℕ], a ∈ B?
پرسش را بر پیشخوان ۲ می‌نهد. سپس بر پاره کاغذی غیب‌گویانه و فراطبیعی پاسخ (درست) آری یا نه را بر پاره کاغذی می‌نویسد و آن را بر پیشخوان ۲ قرار می‌دهد تا نوبتی دیگر که پرسشی بر پیشخوان ۱ بیابد. چنین کاهن غیب‌گویی را یک اوراکل B (برای B) می‌نامیم و آن را با 𝒪(B) نشان می‌دهیم. توجه داریم که 𝒪(B)، یعنی اوراکل B فقط نسبت به مجموعه B، خبرگی غیبب‌گویانه و فرا-طبیعی دارد. بنابراین:
۱- اوراکل دانای مطلق نیست،
۲- اینکه
چگونه اوراکل B برای عضویت عضوی در B
تصمیم می‌گیرد، حتی اگر B تصمیم‌پذیر هم نباشد، مورد پرسش
ما نیست. اوراکل غیب‌گویانه پاسخ را در می‌یابد.
■ ماشین تورینگ اوراکل (Oracle Turing Machine)
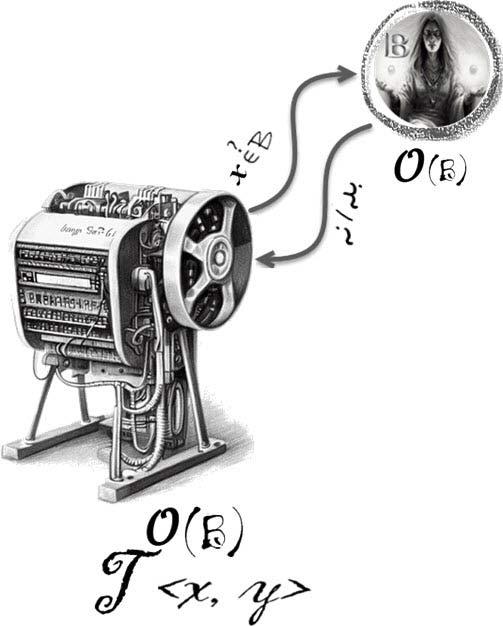
یک ماشین تورینگ اوراکل یک ماشین عادی تورینگ است که مجهز به یک اوراکل، به فرض 𝒪(B)، باشد. یک ماشین تورینگ اوراکل با نمایه x، ورودی y و دسترسی به اوراکل B را با نماد:
T𝒪(B)<x, y>
می‌نویسیم.
■ کاهش‌پذیری تورینگ (Turing reducibility)
گیریم A و B زیرمجموعه‌های اعداد طبیعی و m۱, m۲, ..., mk اعداد طبیعی باشند (k کراندار)، نیز 𝒪(B) اوراکل B باشد. اکنون اگر عضویت n در A کاهش‌پذیر به عضویت یک mi در B با رجوع (یا بدون رجوع) به 𝒪(B) باشد، گوییم A در B رایانش‌پذیر است [نیز A کاهش پذیر تورینگ یا T-کاهش‌پذیر به B است]. در این صورت می‌نویسیم:
A ≤t B.
[در تعریف بالا نقش حضور اوراکل B، یعنی 𝒪(B)، نباید از نظر دور بماند.]
نیز می‌نویسیم:
A <t B ≝ A ≤t B ∧ B ≰t A
☚: گیریم X مجموعه دلخواه؛ ازآنجاکه X≤tX، پس X در X تصمیم‌پذیر است.
توجه به تفاوت ≤m و ≤t ضروری است. در کاهش نگاشتی، یعنی ≤m، یک روند کارآمد عضویت عنصری را در B حساب می‌کند↝. اما در ≤t عضویت آن عنصر در B را 𝒪(B) (غیب‌گویانه) می‌گوید. بنابراین کاهش‌پذیری تورینگ کلی‌تر از کاهش‌پذیری نگاشتی است، یعنی:
چند سطر پایین‌تر (۳) نشان می‌دهیم که وارون رابطه بالا برقرار نیست.
۱: گیریم A یک تصمیم‌پذیر باشد. بنا به تعریف کاهش پذیری تورینگ، برای هر مجموعه دلخواه B داریم:
A ≤t B.
■ مجموعه کامل تورینگ (Turing Complete)
تعریف: گیریم C یک مجموعه c.e باشد. C را کامل تورینگ (T-Complete) گوییم اگر برای هر مجموعه c.e مانند X داشته باشیم:
X ≤t C.
■ هم‌ارزی تورینگ (Turing equivalence)
۵: ≡t یک رابطه هم‌ارزی است و مسئله‌های تصمیم‌پذیری را به کلاس‌های هم‌ارزی (تورینگ) افراز می‌کند.
■ درجه تورینگ (Turing degree)
تعریف. درجه تورینگ:
گیریم A یک مجموعه باشد. بنا به تعریف، درجه تورینگ A (که به آن درجه حل‌ناشدنی A نیز گفته می‌شود) عبارت است از کلاس هم‌ارزی A نسبت به رابطه ≡t. بنابراین می‌نویسیم:
با توجه به آنچه تاکنون گفته شده است:
degt(∅) = degt(ℕ).
[•. این در حالی است که: ↜degm(∅) ≠ degm(ℕ)].
و بطور کلی:
degt(∅) = {A: A_رایانش‌پذیر}.
گیریم degt(A) و degt(B) دو درجه‌یِ تورینگ دلخواه باشند. گوییم درجه تورینگ A پایین‌تر از درجه تورینک B است اگر:
degt(A) < degt(B) .
در ۲.۱ دیدیم
K 
t ∅
بنابراین:
degt(∅) ≠ degt(K).
از آنجا که degt(∅) و degt(K) دو کلاس هم‌ارزی هستند اشتراک آنها تهی است. بنابراین، تا اینجا می‌توانیم بگوییم حداقل دو درجه متمایز تورینگ وجود دارد.
■ پرش تورینگ (Turing jump)
مجموعه توقف قطری (K) که تعریف آن در زیر آمده است را در نظر بگیرید:
نیز فرض کنید A یک مجموعه دلخواه باشد. اکنون مجموعه A' را به قرار زیر تعریف می‌کنیم:
Tj. پرش تورینگ:A' = K𝒪(A) ≝ {x: φ𝒪(A)x (x)↓}.
در واقع در Tj نماد ' یک نگاشت است که مجموعه A را روانه مجموعه K𝒪(A) می‌کند. به عبارت دیگر نگاشت ' مانند یک عملگر وردی خود، یعنی مجموعه A، را به واسطه یک اوراکل به K می‌برد (A را به K / روی K می‌پراند). از این جهت، ' عملگر پرش تورینگ (نگاشت پرش تورینگ) و مجموعه K𝒪(A) پرش تورینگی مجموعه A نامیده می‌شوند.
تابع φ𝒪(A)x (x)↝ را (با توجه به تز چرج-تورینگ) می‌توان معادل ماشین تورینگ اوراکل برای A مطابق زیر در نظر گرفت:
T𝒪(A)<x, T𝒪(A)<x, *>>.
چند ویژگی:
پ.۲: گیریم مجموعه B در مجموعه A رایانشی برشمردنی باشد↝، آنگاه B در A' تصمیم‌پذیر است.↧ به عبارت دیگر، مجموعه‌ای که در اوراکل A رایانشی برشمردنی باشد در اوراکل A' تصمیم‌پذیر خواهد بود.
| B
ر.ب در A |
⇐ | B ر.ب. در A'. |
Borut Robič, The Foundations of Computability Theory (Springer-Verlag Berlin Heidelberg 2015), p. 247.
بنابراین، A و A' دو مجموعه متمایز هستند.
پ.۳: برای مجموعه دلخواه X داریم:
X ≤t X'.
اثبات: از آنجا که X در X تصمیم‌پذیر است، یعنی (X≤tX↝، پس X در X نیمی-تصمیم‌پذیر نیز است↝. اکنون بنا به پ.۲ X در X' تصمیم‌پذیر است.
پ.۴: برای مجموعه دلخواه X داریم:
X' در
X
نیمی-تصمیم‌پذیر است، اما
X' در X
تصمیم‌پذیر
نیست (X'tX).↧
Borut Robič, The Foundations of Computability Theory (Springer-Verlag Berlin Heidelberg 2015), p. 248.
■ سلسله مراتب (پایگان) درجه‌های تورینگ (Hierarchies of Turing-Degrees)
پایگان (سلسله مراتب - Hierarchies) سامانه‌ای است که از سازماندهی چیزها در لایه‌های مختلف بسته به درجه اهمیت آنها (در زمینه مورد مورد نظر) ناشی شده است.
به همان شیوه که در تعریف (برساختن) نگاشت پرش تورینگ، یعنی:
A' = K𝒪(A) ≝ {x: φ𝒪(A)x (x)↓},
دیدیم، نیز می‌توانیم (A')' را تعریف کنیم (برسازیم):
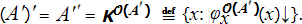
و نیز نتیجه بگیریم:
و نیز:
و سرانجام تعریف زیر را داشته باشیم.
تعریف. پرش nام تورینگ:
پرش nام تورینگ مجموعه A عبارت است از مجموعه A(n)، که به گونه استقرایی به شیوه زیر تعریف شده باشد:
| A(n) ≝ |
 |
| A | اگر n = ۰: |
| (A(n - ۱))' | اگر n ≥ ۰: |
اکنون با توجه به ویژگی‌های پرش تورینگ می‌توانیم بنویسیم:
0 <t 0' <t 0'' <t 0''' <t . . .. ↜
| پایگان (سلسله مراتب) درجه‌های تورینگ (Jump hierarchy of Turing-degrees) |
|
| . . . |
|
| 0'' | |
| مجموعه توابع کامل، مجموعه توابع متناهی، . . .. | 0'' |
| بزرگترین درجه تورینگ برای مجموعه‌های c.e (مجموعه توقف، مجموعه توقف قطری، توقف تابع فراگیر، ناتمامیت گودل، . . .. ) | 0' |
| درجه تورینگ مجموعه‌های رایانش پذیر. | 0 |
رابطه بالا پایگان (سلسله مراتب) پرشی مجموعه‌ها (Jump hierarchy of sets) نامیده می‌شود. به رابطه نظیر آن یعنی:
deg(0) <t deg(0') <t deg(0'') <t . . .
پایگان (سلسله مراتب) درجه‌های تورینگ (Jump hierarchy of T-degrees) گفته می‌شود.
قضیه کلین-پست (Kleene-Post Theorem)
مجموعه‌های رایانش‌پذیر برشمردنی A و B (یعنی A, B ≤t 0') وجود دارند به
قسمی که AtB و BtA.↧ به
عبارت دیگر می‌توان نوشت:
Robert I. Soare. (2016), Turing Computability, Theory and Applications. Springer-Verlag Berlin Heidelberg. p. 132.
باتوجه به قضیه کلین-پست فشرده‌ای از آنچه پیشتر در این قسمت آمده است در شکل زیر (ش. ۲) نشان داده شده است.
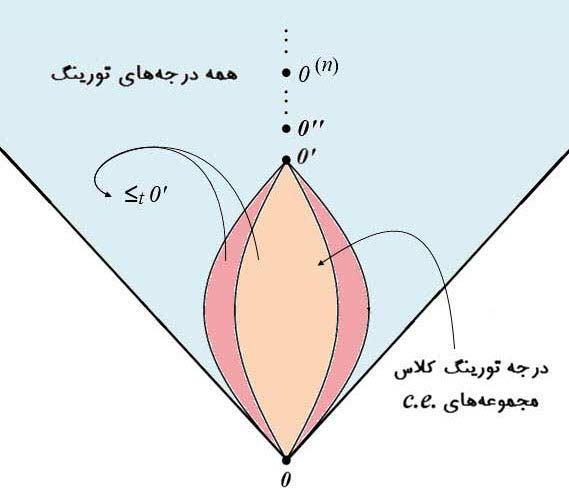
Robert I. Soare. (2016), Turing Computability, Theory and Applications. Springer-Verlag Berlin Heidelberg. p. 63.
■ پایگان درجه‌های نگاشتی و پایگان درجه‌های تورینگ
برای یاد آودری، در شکل زیر (ش. ۳) نمایی از آنچه پایگان درجه‌های نگاشتی نامیده می‌شود آمده است.
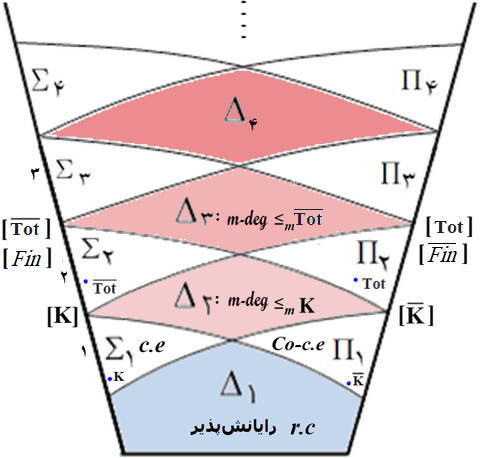
در شکل پایین (ش. ۴) نیز دو پایگان درجه‌های نگاشتی و درجه‌های تورینگ به صورت ادغام شده به نمایش در آمده است.
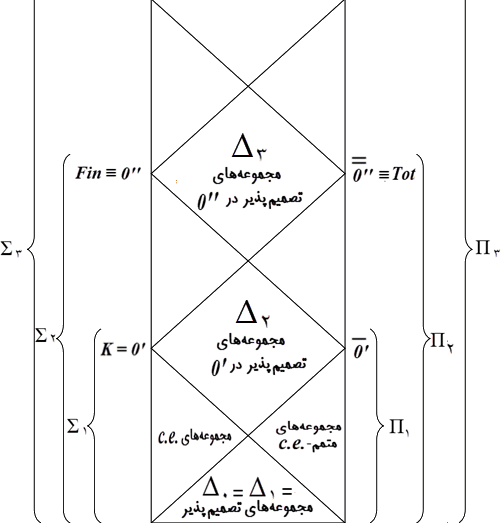
Robert I. Soare. (2016), Turing Computability, Theory and Applications. Springer-Verlag Berlin Heidelberg. p. 104.
منابع و ارجاعات
1- Davis, Martin, editor.
The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Corr. republ, Dover Publication, 2004.
2- Davis, Martin. The Universal Computer: The Road from Leibniz to
Turing. CRC Press/Taylor & Francis Group, 2018.
3- Davis, Martin, Hilbert's Tenth Problem is Unsolvable, The American Mathematical Monthly, Vol. 80, No. 3 (Mar., 1973), p. 233-269.
4- Alonzo Church. An Unsolvable Problem of Elementary Number Theory, American Journal of Mathematics, Vol. 58, No. 2. (Apr., 1936) pp. 345-363. https://www.ics.uci.edu/~lopes/teaching/inf212W12/readings/church.pdf
5- Stephen Cole Kleene. Mathematical logic, Dover Publications (December 18, 2002).
6- Nigel Cutland. Computability: An introduction to recursive function theory, Cambridge University Press, (1980.)
7- AM Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1938.
8- Adams, R. J. L. An Early History of Recursive Functions and Computability from Godel to Turing. (2011).
9- J. C. Shepherdson und H. E. Sturgis. Computability of recursive functions. Journal of the Association for Computing Machinery, Bd. 10 , S. 217–255. (1963)
10- George Tourlakis, Computability, Springer International Publishing. (2022.)
11- Robic, B. The Foundations of Computability Theory. In Springer eBooks. Springer Nature. (2015.)
12- Hartley Rogers, Jr· Theory of Recursive Functions and Effective Computability. The MIT Press; Fifth Printing edition (April 22, 1987).
13- Herbert B. Enderton An Introduction to Recursion Theory. Academic Press is an imprint of Elsevier (2011).
14. Dean, Walter, "Recursive Functions", The Stanford Encyclopedia of Philosophy (Winter 2021 Edition), Edward N. Zalta (ed.)
15- S. Barry Cooper. Computability theory. Chapman & Hall/CRC mathematics (2003.)
16- Robert I. Soare. (2016), Turing Computability, Theory and Applications. Springer-Verlag Berlin Heidelberg.
17- Robert I. Soare. (1987), Recursively Enun1erable Sets and Degrees. Springer-Verlag Berlin Heidelberg.
 |  |