ماشین تورینگ و حل مسئله
منطق و نظریه رایانش (۸)
درآمد به منطق
ماشین تورینگ یک مدل منطقی / ریاضی است که از آن برای درک نحوه اجرای (منطق) الگوریتمها توسط کامپیوتر استفاده میشود. در واقع یک ماشین تورینگ منطق یک الگوریتم را شبیه سازی میکند. در قسمتهای پیشین منطق و نظریه رایانش به ماشین(های) تورینگ به عنوان یک مدل رایانش اشاره شده است. از جمله در قسمت ماشینهای اندوختگانی توضیح درخور آن قسمت در باره ماشینهای تورینگ آمده است. [همانجا یادآوری شد که درک آسان و نیز سهولت برنامه نویسی ماشینهای اندوختگانی علت انتخاب آنها به عنوان مدل نظری رایانش در آنجا است]. این بخش، با در نظرداشتن تز چرج-تورینگ، بر روی ماشین(های) تورینگ به عنوان یک مدل نظری رایانش تمرکز میکند،.
 ماشین تورینگ و حل مسئله
ماشین تورینگ و حل مسئله
۱- مقدمه | ۸- مثال ۱. ماشین تورینگ - برگردان (Conversion) |
۲- حالت و قاعده گذار (State and Transition Rule) | ۹- مثال ۲. ماشین تورینگ - واروخوانگی (Palindrome) |
۳- ماشین تورینگ و تز چرچ-تورینگ | ۱۰- ماشین تورینگ جهانی (Universal Turing machine) |
۴- ساختار ماشین تورینگ | ۱۱- ماشینهای تورینگ قطعی و غیر قطعی. |
۵- روش نموداری نمایش ماشین تورینگ | ۱۲- دو مسئله تصمیمناپذیر |
۶- ماشین تورینگ و حل مسئله | ۱۳- ماشین تورینک و کامپیوترهای امروزی |
۷- مسئله توقف (Halting problem) |
■ مقدمه
در قلمرو علوم کامپیوتر ماشین تورینگ، که به عنوان یک انگاشته بنیادین برپای ایستاده است، یک مدل نظری رایانش است که آلن تورینگ آن را در ۱۹۳۶ پدید آورد↝. این ماشین، به عنوان یک مدل منطقی / ریاضی، یک ماشین انتزاعی را تعریف میکند. این مدل انتزاعی منطق الگوریتمها را شبیهسازی میکند و چارچوبی برای بررسی نحوه پردازش اطلاعات توسط کامپیوترها فراهم میکند. ماشینهای تورینگ در بحثهای مربوط به مدلهای رایانشی (محاسباتی) محوری بودهاند و به عنوان سنگ بنای نظریه رایانش عمل میکنند.
یک ماشین تورینگ مطابق با تعداد محدود از قواعد موسوم به قواعد گذار (Transition rules) در گذار از حالتی به حالتی به انجام عملیات بر روی نمادهای (زبان) نوشته شده بر باریکهای نواری میپردازد. و در واقع، همین حالتها و قواعد گذار هستند که سیستم (در اینجا ماشین تورینگ) را تعریف میکنند.
■ حالت و قاعده گذار
همانطور که در مقدمه گفته شد، یک ماشینهای تورینگ با حالتها و قواعد گذار بین آنها معین و متمایز میشود. بنابراین پیش از تعریف ماشین تورینگ، نیاز است تا به دو مفهوم اساسی «حالت / ایستانه / State» و «قواعد گذار / Transition Rules» توجه ویژه داشته باشیم.
•: حالت (یا ایستانه / State) یک سیستم وضعیت سیستم را در یک زمان معین به شمول همه اطلاعات مربوط به سیستم در آن زمان را تعریف میکند. میتوان یک حالت را همچون یک عکس فوری از سیستم در یک نقطه خاص از زمان دانست. معمولاً یک حالت با مجموعهای از گزارهها توصیف میشود که در آن نقطه از زمان برقرار (درست) هستند. رفتار سیستم با گذار بین حالتها توصیف میشود.
•: قاعده گذار (Transition Rule) در یک سیستم چگونگی گذار (انتقال) یک دستگاه از یک حالت به حالتی در آن دستگاه را تعریف میکند.
بازی و صفحه شطرنج شاید مناسبترین مثال برای توضیح این دو، یعنی ایستانه و قواعد گذار باشد. در شکل زیر دو حالت ممکن (از میان حالتهای ممکن دیگر) بعد از آغاز شطرنج آمده که هر کدام بر اساس دو قاعده گذار در شطرنج رخ داده است.
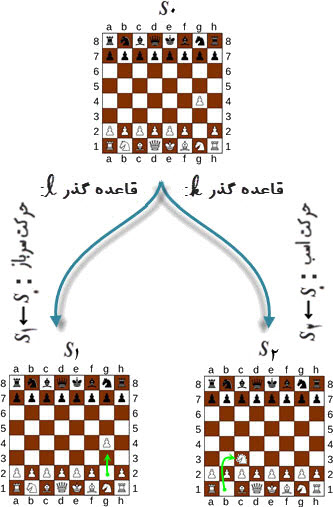
شکل ۱. ایستانه / حالت / State.
چینش آغازین یک بازی شطرنج (حالت S۰) و گذار به یکی از حالتهای ممکن بعدی (در اینجا S۱ و S۲). قاعدههای 𝓁 و k به ترتیب یکی از قواعد گذار حرکت سرباز و اسب هستند.
نکته مهمی که باید به آن توجه کرد این که در شطرنج انتخاب مهرهها برای حرکت و قاعده حرکت (توسط بازیکن) اگرچه محدود است اما به گونهای نامتعین است. در ماشین تورینگ معمولی که به آن ماشین قطعی (الگوریتم قطعی) میگویند، همانطور که خواهیم دید، این عدم تعین وجود ندارد. در ادامه این قسمت به طور کوتاه در باره ماشین تورینگ غیرقطعی نیز توضیح خواهیم داد.
■ ماشین تورینگ و تز چرچ-تورینگ
هر ماشین تورینگ یک سازواره ماشینی (machinery) رایانشی↝ است. به عبارت دیگر، بنا بر تز چرج-تورینگ، برای هر تابع بازگشتی جزئی یک ماشین تورینگ وجود دارد و نیز بر عکس آن. و همینطور، برای هر الگوریتم یک ماشین تورینگ وجود دارد و البته نه لزوماً برعکس آن↝.
■ ساختار ماشین تورینگ

شکل ۲. شمای ماشین تورینگ.
یک ماشین تورینگ شامل:
۱- زبان Σ به قسمی که Σ ≠ ∅، با الفبای متناهی و فاقد حرف خالی '#' (خالی - فاصله space - empty - blank) است. ورودی ماشین برای پردازش به زبان Σ نوشته میشود.
۲- ورودی (Input): که رشتهای متناهی به زبان Σ است.
۳- زبان Γ با الفبای متناهی و شامل نویسههای Σ، نویسه '#' و احتمالاً نویسههای بیشتر.
بنابراین داریم:
•: '#' ∈ Γ،
•: '#' ∉ Σ،
•: ∅ ≠ Σ ⊂ Γ.

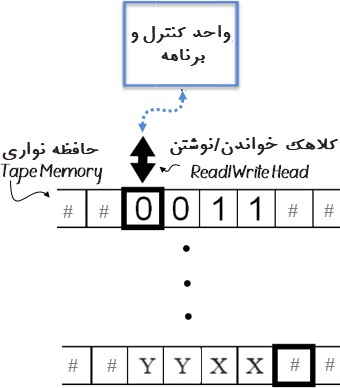
۴- حافظه خطی به نام نوار حافظه (یا فقط نوار / Tape). این نوار به خانههای هماندازه، که تعداد آنها میتواند از یک جهت نامحدود باشند، تقسیم شده است. به عبارت دیگر، تعداد خانههای نوار میتواند از یک جهت به هر اندازه مورد نیاز گسترش یابند. هر خانه این نوار میتواند شامل یک نویسه Γ باشد.
۵- کلاهک خواندن / نوشتن (Read-Write Head) با توان خواندن و نیز نوشتن (بازنویسی) نویسههای Γ در خانه نوار حافظه روبروی کلاهک (یک نویسه در یک خانه).

در آغاز کار ماشین، کلاهک روبروی اولین خانه حاوی ورودی روی نوار قرار میگیرد. کلاهک امکان لغزیدن به اندازه یک خانه به خانههای مجاور را دارد و بنابراین میتواند بر روی هر خانه نوار قرار گیرد. و از اینجا، محتوی خانه روبرو را برای پردازش در دسترس قرار دهد.
۶- مجموعه حالتها: مجموعه متناهی 𝒮 از حالتها (States) به شمول یک حالت با نام حالت آغازی SI (Initial state) و حداقل یک حالت با نام حالت پایانی ST (Final state). اگر مجموعه حالتهای پایانی را 𝓕 بنامیم آنگاه:
∅ ≠ 𝓕 ⊂ 𝒮.
۷- قواعد گذار (Transition Rules): مجموعه متناهی از قواعده گذار (نیز موسوم به دستورالعملها / برنامه تورینگ / تابع گذار). درواقع، صورت قواعد گذار (برنامه) تابع جزئی δ است که به قرار زیر تعریف شده است:
T.F. δ : 𝒮 × Γ → 𝒮 × Γ × D ; D = {→, ←, ■}.
→: برای حرکت کلاهک یک خانه به سمت راست در یک گام اجرایی (چرخه - سیکل - Cycle).
←: برای حرکت کلاهک یک خانه به سمت چپ در یک گام اجرایی (چرخه).
■ : برای بدون حرکت ماندن کلاهک در یک گام اجرایی (چرخه).
توجه ☚: تابع گذار یک ماشین تورینگ مشخصه همان ماشین خاص است و به عبارت دیگر ماشینهای تورینگ مختلف دارای توابع مشخصه متفاوت هستند.
• واحد کنترل:
واحد کنترل یک ماشین تورینگ قسمتی است که در آن برنامه تورینگ آن ماشین جای دارد. واحد کنترل همیشه در یکی از حالتهای 𝒮 قرار دارد و در آغاز کار ماشین، حالت واحد کنترل حالت آغازین است. واحد کنترل از طریق کلاهک خواندن/نوشتن میتواند به نماد روبروی کلاهک دسترسی داشته باشد. به عبارت دیگر، واحد کنترل میتواند نویسه خانه روبروی کلاهک را بخواند یا آن نویسه را با نویسهای رونویس کند. در هر گام، کلاهک میتواند تنها به یکی از خانههای مجاور خانه جاری حرکت کند.
■. چرخه (Cycle):
فرض کنید واحد کنترل از حالت Sg به حالت Si گذار کرده و کلاهک روبروی خانهای از نوار با محتوی 'b' است. نیز فرض کنید مقدار تابع گذار برای برای ورودیهای Si و 'b' به قرار:
δ (Si, 'b') = ('c', Sk, →).
است و Si یکی از حالتهای پایانی نیست. این مقدار تابع گذار توسط واحد کنترل به گونه زیر تعبیر (اجرا) میشود:
۱- محتوی خانه روبروی کلاهک با 'c' جایگزین گردد،
۲- کلاهک یک خانه به سمت راست (→) حرکت کند،
۳- واحد کنترل در حالت Sk قرار داده شود.
بعد از چرخه بالا نوبت به چرخه بعدی به همان ترتیبی که گفته شد میرسد، اما این بار برای ورودی Sk و نویسه خانه روبروی کلاهک. واحد کنترل به همین روش، تا زمانی که واحد کنترل در یکی از حالتهای پایانی قرار بگیرد، اجرای چرخهها را ادامه میدهد. در پایان اجرا، یعنی وقتی واحد کنترل در یکی از حالتهای پایانی قرار گرفته است، باید خروجی برنامه (پاسخ مسئله مورد پرسش) در نوار نوشته شده باشد. البته توجه داریم که ممکن است تابع گذار به هر علت بد نوشته شود، به گونهای که واحد کنترل هیچ گاه به یکی از حالتهای پایانی نرسد (پایانپذیری الگوریتم / ماشین بیپایان) و یا پاسخ صحیح را برای برخی ورودی به دست ندهد (صحت الگوریتم).
در شکل زیر خلاصهای از آن چه گفته شد به تصویر در آمده است.
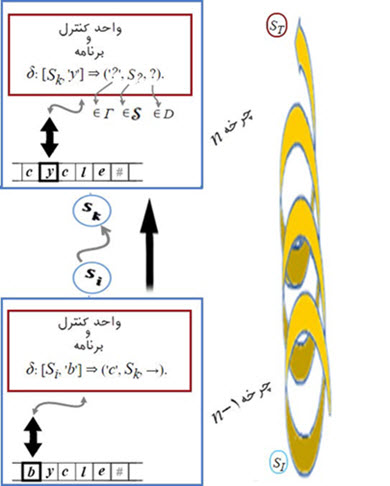
شکل
۳. اجرای یک چرخه از
تابع گذار در ماشین تورینگ.
در این نمودار دو ویژگی (توالی و انتخاب) از وسه
ویژگی بنیادی الگوریتم آشکارا
نمایان است.
■ روش نموداری نمایش ماشین تورینگ
فرض کنید مقدار تابع گذار یک ماشین تورینگ برای ورودیهای Si و 'b' به قرار زیر باشد:
δ (Si, 'b') =('c', Sk, →).
رابطه بالا را بهصورت زیر با نمودار نشان دهیم:
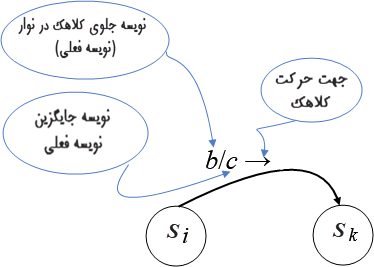
شکل ۴. نمودارسازی مقدار یک تابع گذار ماشین تورینگ.
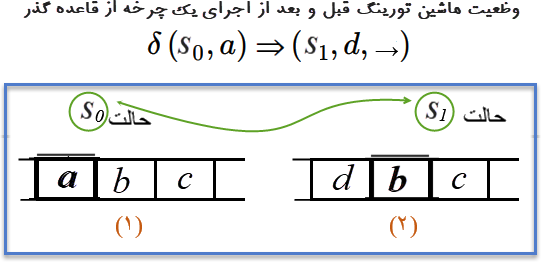
■ ماشین تورینگ و حل مسئله

اکنون و بنا بر آنچه تا اینجا آمده است میتوان در باره ماشین تورینگ و حل مسئله گفت:
برای رایانش یک تابع (حل یک مسئله) باید یک ماشین تورینگ ساخت که چینش حالتها و تابع گذار آن به گونهای باشد که با آغاز به کار ماشین (حالت آغازی Si)، در زمان محدود منجر به یکی از حالتهای پایانی شود و در این حالت جواب (صحیح) مسئله در حافظهی نواری نوشته شده باشد.
■ مسئله توقف (Halting problem)
«مسئله توقف» در قسمت «تصمیمپذیری و روش کاهش در حل مسئله» به تفصیل مورد بحث قرار گرفته است. بنا بر تز چرج-تورینگ همه آنچه در بحث توقف گفته شده است برای ماشین تورینگ نیز صادق است. به عبارت دیگر، برخی ماشین تورینگ (بعضی برنامه) برای برخی ورودی پایانپذیر نیست. یعنی، برخی ماشین تورینگ مدل یک روند کارآمد نیست. مسئله توقف را میتوان مطابق زیر برای ماشن تورینگ بازآرایی کرد:
آیا میتوان
یک ماشین تورینگ به فرض Halt![]() ساخت که به عنوان ورودی برنامه
(کد برنامه) ماشین تورینگ دلخواه دادهشدهای به فرض
P را بپذیرد و در باره پایانپذیری
P برای ورودی دلخواه به فرض x تصمیمگیری کند؟ به عبارت دیگر آیا تابع:
ساخت که به عنوان ورودی برنامه
(کد برنامه) ماشین تورینگ دلخواه دادهشدهای به فرض
P را بپذیرد و در باره پایانپذیری
P برای ورودی دلخواه به فرض x تصمیمگیری کند؟ به عبارت دیگر آیا تابع:
Halt![]() (P,
x)
(P,
x)
| اگر (P, x) پایان پذیر است: | بله |
Halt |
|
| اگر (P, x) پایان ناپذیر است: | نه |
تصمیمپذیر (محاسبهپذیر) است؟ (تصمیم ناپذیری مسئله توقف و توقف قطری را ببینید.)
■ مثال ۱. ماشین تورینگ - برگردان (Conversion)
فرض کنید ورودی ماشین در این مثال به قرار رشتهای از n صفر '0' و بلافاصله در پی آن n یک '1' است. برای نمونه، رشتههایی مانند '0011' و مثل آنها. خروجی باید برگردان نویسههای '0' به 'X' و نویسههای '1' به 'Y' در ورود باشد. برای مثال، برای ورودی '0011' خروجی باید 'XXYY' باشد.
برای ساختن این ماشین ابتدا باید تابع گذار آن را تعریف کرد. تابع گذار معمولاً در یک ساختار جدولی (ماتریس) نشان داده میشود. به چنین جدولی جدول گذار ماشین تورینگ گفته میشود. خانههای این جدول مقدار تابع گذار است. مقادیر ورودیهای تابع گذار، یعنی اعضای Γ و 𝒮، به ترتیب در سطر اول در ستون مربوط و ستون اول در سطر مربوط آن خانه نوشته شده است. در شکل زیر ساختار جدول گذار ماشین تورینگ آمده است.
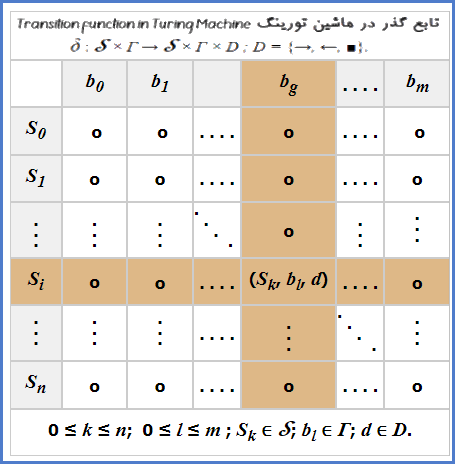
اینک به تعریف (ساختار) ماشین این مثال میپردازیم:
۱. {S0,
S1, S2,
S3, St} =
𝒮
- St حالت پایانی است.
۲.
{0, 1} = Σ
۳.
{0,
1, X, Y, #} = Γ
۴. تابع گذار به قرار زیر:
| 0 | 1 | X | Y | # | |
| S0 | (S1, X, →) | - | - | (S3, Y, →) | - |
| S1 | (S1, 0, →) | (S2, Y, ←) | (S1, Y, →) | - | |
| S2 | (S2, 0, ←) | - | (S0, X, →) | (S2, Y, ←) | - |
| S3 | - | - | - | (S3, Y, →) | (St, #, →) |
| St | - | - | - | - | - |
افزون بر جدول گذار میتوان یک ماشین تورینگ را با نموداری به نام نمودار حالت↝ (نیز ماشین گذار حالت) نشان داد. در زیر چنین نموداری برای این مثال آمده است.
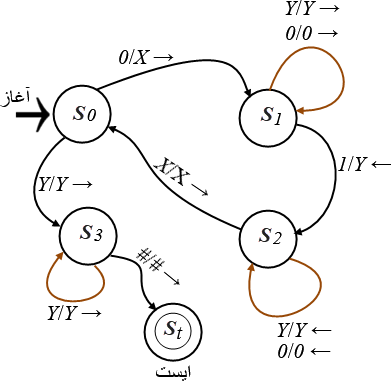
■ مثال ۲. ماشین تورینگ - واروخوانگی (Palindrome)
چینش حروف برخی واژگان در یک زبان به گونهای است که از چپ یا راست یکسان خوانده میشوند (مانند “۱۸۸۱”، “level” یا “گرگ”). به این واژگان واروخوانه (Palindrome) میگویند. در این مثال، یک ماشین تورینگ را میبینیم که درباره واروخوانه بودن ورودی خود تصمیمگیری میکند. یک واژه واروخوانه در یک زبان را میتوان به صورت بازگشتی مطابق زیر تعریف کرد:
۱. یک تک حرف، به شمول نویسه خالی '#'، یک واژه واروخوانه است.
۲. اگر X و Y واژگان واروخوانه باشند آنگاه YXY واروخوانه است.
بند ۲ تعریف را میتوان اگر چه نه به این دقت اما راحتتر چنین نیز بیان کرد:
اگر X یک واژه غیر-خالی و نیز واروخوانه باشد، آنگاه واژه حاصل از خالی کردن نویسههای سمت چپترین و سمت راستترین در X یک واروخوانه است. برای مثال اگر X برابر 'level' باشد، '#eve#' نیز واروخوانه است.
آنچه در پی میآید پیاده سازی این تعریف (تعریف بازگشتی) واروخوانگی در قالب ماشین تورینگ است. در زیر Σ↝ و Γ↝ معرفی شدهاند. حالتها و قواعد گذار نیز در نمودار حالتها نشان داده شدهاند.
۱.
{a, b} = Σ
۲.
{a, b, #} =
Γ.
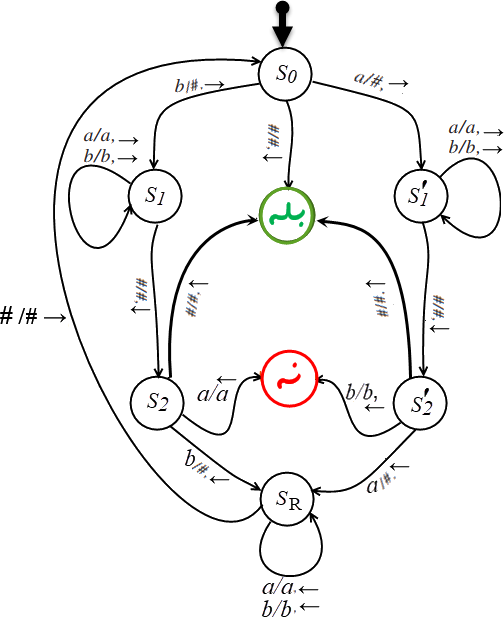
در نمودار زیر ردیابی مثال ۲ برای ورودی "abba" به نمایش در آمده است.
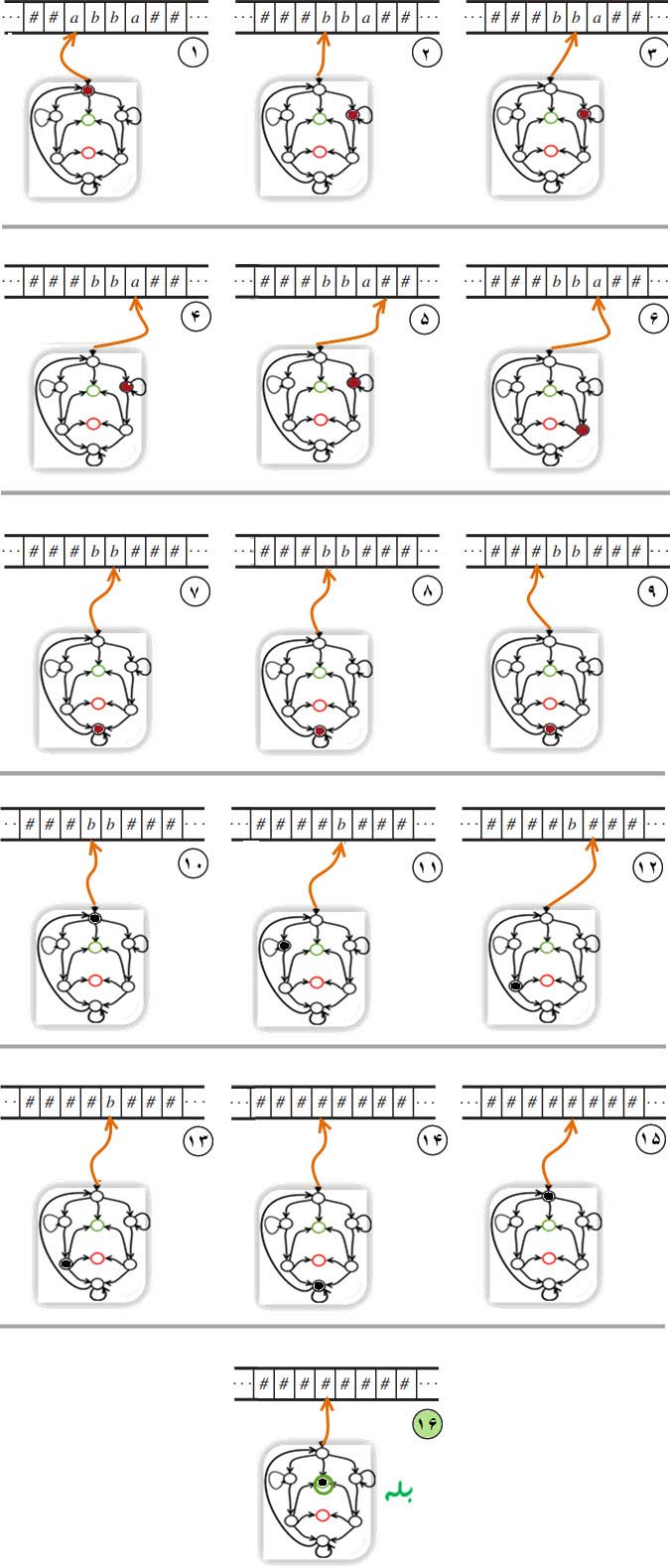
David Harel, Yishai, Algorithmics. The Spirit of Computing. (Pearson Education Limited, 3thd Ed. 2004), p. 225.
در زیر میتوانید یک قطعه کد (تابع) را بیابید که در مورد واروخوانگی یک رشته تصمیم میگیرد.
{
if (len < 2) return true;
else if (InputString[0] != InputString[len-1]) return false;
else if (len == 2) return true;
else return IsPalindrome(InputString.Substring(1, len - 2));
■ ماشین تورینگ جهانی (Universal Turing machine)

همانطور که تا اینجا دیدیم برای اجرای هر الگوریتم باید ماشین تورینگ خاص آن الگوریتم ساخته شود. از این جهت مفهوم ماشین تورینگ جهانی (Universal Turing Machine / UTM) معرفی شده است. ورودی UTM توصیف یک ماشین تورینگ (حالتها و قواعد گذار) به فرض Ti است↝.
به عبارت دیگر، ماشین تورینگ جهانی (UTM) ماشین تورینگی است که قادر است آنچه را که هر ماشین تورینگ دیگری رایانش میکند رایانش کند و با فرض درستی تز چرج-تورینگ، ماشین تورینگ جهانی میتواند هر آنچه را که "رایانشپذیر" است رایانش کند. و به وارون، هر آنچه توسط ماشین جهانی تورینگ قابل رایانش نیست رایانش پذیر به حساب نمیآید.
یک ماشین تورینگ جهانی UTM باید دو ویژگی زیر را برآورد:
۱- هر ماشین تورینگ Ti↝ را بفهمد↝؛
۲- و برمبنای (۱) Ti
را همانندسازی (رفتار
Ti
را تقلید) کند.
توضیح بیشتر و اهمیت این ماشین در نظریه رایانش را میتوان در بحث «تابع جهانی» در قسمت «توابع بازگشتی جزئی و ماشین جهانی» یافت.
■ ماشینهای تورینگ قطعی و غیر قطعی
ماشینهای تورینگ را که تا اینچا دیدیم ماشین تورینگ قطعی (Deterministic Turing machine / DTM) نام دارند. قطعیت (Determinism) در ماشینهای DTM بدین معنی است که در این ماشینها برای هر حالت و نماد فقط یک گذار وجود دارد. برخلاف DTM یک ماشین تورینگ غیر-قطعی (Nondeterministic Turing machine / NTM) میتواند چندین گذار برای یک حالت و نماد داشته باشد. این یعنی، با توجه به یک پیکربندی خاص، یک NTM میتواند چندین پیکربندی بعدی ممکن را داشته باشد.
میتوان تصور کرد که یک ماشین NTM میتواند مسیر رایانش صحیح را «گمانه زنی» کند. و اگر حداقل یک مسیر رایانش وجود داشته باشد که به حالت صحیح منتهی شود، آنگاه NTM پذیرنده ورودی خواهد بود. این جنبه از NTM ها آنها را در برخی موارد تواناتر از DTM ها میکند. با این حال، هنوز این یک پرسش باز است که آیا NTMها از نظر توانایی آنها در حل مسئله قدرتمندتر از DTMها هستند. در قسمتهای بعدی منطق و نظریه رایانش به این مورد باز خواهیم گشت. باید توجه داشت که مسئلههای حل نشدنی برای NTM نیز حل نشدنی است↝.
■ دو مسئله تصمیمناپذیر
آ. همارزی↝ دو ماشین تورینگ تصمیمپذیر نیست. و از اینجا، بنا بر تز چرج-تورینگ همارزی دو تابع رایانشپذیر جزئی تصمیمپذیر نیست.
اثبات:
فرض میکنیم T یک ماشین تورینگ داده شده باشد. ماشین تورینگ T' را به گونه زیر تعریف میکنیم:
| T'(x) = |  |
| T(x) | اگر x ≠ T [نمایهسازی توابع رایانشپذیر جزئی را ببینید.] |
 | اگر x = T [یعنی وقتی T'(x)=T'(T) که در این حالت ماشین T' ماشین T را همانند سازی میکند]: |
بنابراین T و T' همارز↝ هستند اگر و فقط اگر T(T) متوقف نشدنی باشد. و از اینجا، ماشینی که بخواهد در باره همارزی T و T' تصمیم بگیرد باید بتواند در باره توقف T(T) تصمیم بگیرد و این خود منجر به تناقض خواهد شد (مسئله توقف قطری / K را ببینید). پس دو ماشین تورینگ T و T' هستند (به فرض وجود T) که همارز هستند و همارزی آنها تصمیم پذیر نیست.)
ب. همارزی دو ماشین تورینگ پایانپذیر تصمیمپذیر نیست. و از اینجا، بنا بر تز چرج-تورینگ همارزی دو تابع رایانشپذیر تصمیمپذیر نیست.
اثبات:
فرض میکنیم T یک ماشین تورینگ داده شده باشد. ماشین تورینگ T' را به گونه زیر تعریف میکنیم:
| T' = |  | |
| ۱ | اگر
T(T) ←  : : | T'(x) بنا به تعریف پایانپذیر است. |
| ۰ | وگر نه: |
ماشین T'' را نیز به گونه زیر تعریف میکنیم:
| T'' = |  | |
| ۱ | برای هر ورودی: |
بنابراین T'' نیز پایانپذیر است. اما، T' ≃ T'' اگر و فقط اگر ماشین تورینگ برآورد کننده این همارزی توانا به تصمیم گرفتن به پایانناپذیری T(T) باشد، که این (مسئله توقف قطری / K) غیرممکن است. (پس دو ماشین تورینگ T' و T'' هستند (به فرض وجود T) که پایانپذیر و همارز هستند و همارزی آنها تصمیم پذیر نیست.)
■ ماشین تورینک و کامپیوترهای امروزی

همانطور که دیدیم، ماشین تورینگ به عنوان یک مدل نظری رایانش قادر به پیاده سازی الگوریتمهای کامپوتری (الگوریتمی که برای پیاده سازی در کامپیوتر طراحی شده) است و به طور گسترده به عنوان پایه و اساس علوم کامپیوتر مدرن در نظر گرفته میشود. از دیگر سو، کامپیوترهای امروزی (نیز موسوم به کامپیوترهای فون نویمانی↝) بر مبنای معماری فون نویمان هستند که در سال ۱۹۴۵ عمدتاً توسط جان فون نویمان پیشنهاد شد. معماری فون نویمانی بر اساس مفهوم برنامه ذخیره شده است، جایی که برنامه و هم دادهها در یک واحد ذخیره سازی جداگانه به نام حافظه ذخیره میشوند و با آنها (یعنی برنامه و داده) یکسان رفتار میشود. معماری فون نویمان، افزون بر حافظه شامل واحد مرکزی پردازش - CPU - Central Processing Unit (به شمول واحد منطق حسابی - ALU - Arithmetic Logic Unit، رجیسترها و واحد کنترل)، نیز مکانیزم های ورودی/خروجی است.
جان فون نویمان نقش مهمی در توسعه معماری مدرن کامپیوتر ایفا کرد. پیشنهاد او از مفهوم برنامه ذخیره شده و معماری فون نویمان، پایه و اساس طراحی کامپیوترهای امروزی را بنا نهاد. معماری فون نویمان نشان داده است که یک طراحی انعطاف پذیر و قدرتمند است که آزمون زمان را پس داده است.
به طور خلاصه، در حالی که ماشین تورینگ و کامپیوترهای امروزی هر دو قادر به پیاده سازی الگوریتمهای رایانهای هستند، در طراحی و قابلیتهای خود متفاوت هستند. ماشین تورینگ یک مدل نظری است که پایهای برای درک محاسبات فراهم میکند، در حالی که کامپیوترهای امروزی مبتنی بر معماری عملی فون نویمان هستند. جان فون نویمان با پیشنهاد مفهوم برنامه ذخیره شده و معماری فون نویمان نقش مهمی در پر کردن شکاف بین نظریه و عمل ایفا کرد.
