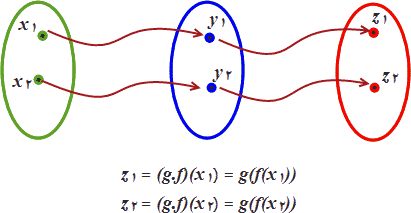
■ تابع (نگاشت)

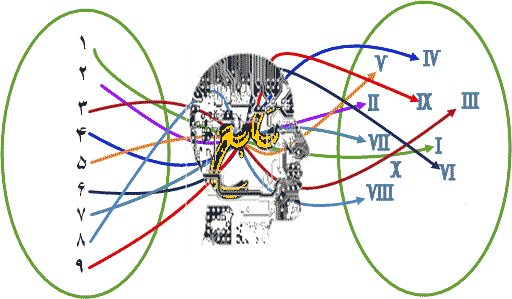
یک تابع [یا نگاشت نیز تابع کامل] وقتی از S در T تعریف میشود که برای هر عضو S یک و فقط یک عضو از T مصور باشد (عضوی در S بدون تصویر باقی نماند و فقط هم یک تصویر در T داشته باشد). با توجه به تعداد عضوهای S و T میتوان چندین تابع از S به T تعریف کرد (از چندین نظرگاه در S به T نگاه کرد.) بنابراین، با تعریف هر تابع از S به T یک تصویر S را در T خواهیم داشت. معمولاً توابع را با حروفی کوچک لاتین مانند g ،f و مانند آنها نامگذاری میکنند. وقتی تابعی از S در T بنام f تعریف شود، این تعریف را بهصورت شماتیک:
f : S→T
<f, S, T> و نیز
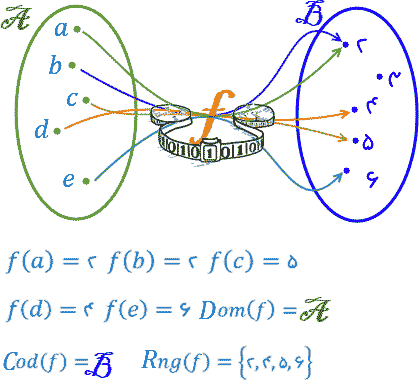
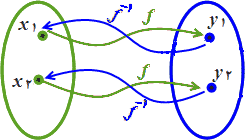
نشان میدهند. S را دامنه تابع و نیز مجموعه آغازی تابع نامیده [نشان داده با Dom(f)]. زیرمجموعهای از Tکه اعضای آن تصویر عضوی از S هستند را برد تابع مینامند [نشان داده با Rng(f)]. خود مجموعه T قلمرو تابع و نیز مجموعه انجامی تابع نام دارد [نشان داده با Cod(f)].
مهم اول در تعریف یک تابع این نیست که چگونه تصویر یک عضو دامنه را باید پیدا کرد، مهم اول شناسایی مجموعههای آغازی و انجامی و نشان دادن یا فرض کردن اینکه: «همه عناصر مجموعه آغازی تحت تابع تعریفشده دارای یک و فقط یک تصویر در مجموعه انجامی است».
عبارت داخل گیومه را معمولاً اینگونه مینویسند:
برای هر x∈S اگر،x آنگاه f(x)∈T
در عبارت بالا به (f(x مقدار تابع p;f برای x یا تصویر x تحت تابع f میگویند.
مسئله بعد میتواند این باشد که برای یک x خاص در S چگونه میتوان (f(x را یافت. روشهای مختلف برای این کار هست که بستگی به مجموعههای انجامی و آغازی و مهمتر قصد تعریف تابع دارد. ازجمله نوشتن یک عبارت جبری است که به آن ضابطه تابع نیز میگویند. برای مثال فرض کنید S و T هردو  باشند، آنگاه:
باشند، آنگاه:
e : →
→  ; e(x)=۲x-۱.
; e(x)=۲x-۱.
یک بیان از e میتواند این باشد که، برای هر عدد طبیعی یک عدد فرد نظیر وجود دارد (توجه: ما صفر را عدد طبیعی فرض نکردهایم.) طریقههای دیگری ازجمله رسم نمودارهای مختلف و همینطور جداول مرسوم است.
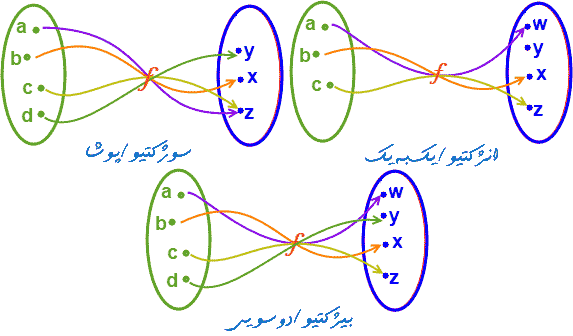
به تابع f یک تابع یکبهیک [انژکتیو - درونی / اندرونی / جاسازی شده / Injective / one to one / Embedded] (بهصورت نمادین ۱:۱) میگویند اگر و فقط اگر عضوی در Tنباشد که تصویر دو عضو متمایز Sباشد. بهعبارتدیگر، اگر a و b دو عضو متمایز S باشند، آنگاه (f(a و (f(b، یعنی تصاویر آنها، نیز متمایز باشند. [برای مثال، تابع e در بالا ۱:۱(یکبهیک) است.]
اگر برد تابع همه T باشد (عضوی در T نیست که تصویر عضوی از S نیست) آنگاه به f یک تابع پوشا / Onto [سابجکتیو Surjective / Subjective /] گفته میشود. [تابع e در بالا پوشا نیست.] اما تابع :
d: ↦ E ; d(x)=۲x-۱
↦ E ; d(x)=۲x-۱
که در آن E مجموعه اعداد فرد است پوشا است.
تابعی که هم ۱:۱ و هم پوشا باشد را تابع دو سویی [بیژکتیو / جاسازی شده / Bijective] میگویند.
اگر f دو سویی باشد آنگاه بهخودیخود یک تابع دیگر از T در S تعریف میشود. برای نشانهگذاری این تابع از حرف جدیدی استفاده نمیشود و آن را با f -۱ نشانهگذاری میکنند و به آن تابع وارون f گفته میشود [در ادامه همین قسمت از تابع وارون بیشتر میگوییم.]
اگر f دو سویی باشد میگوییم بین S و T یک تناظر یکبهیک (بهواسطه f) برقرار است.
فرض کنید A و B دو مجموعه، گوییم بین این دو یک رابطه تناظر وجود دارد اگر حداقل یک تابع دو سویه از یکی از آنها در دیگری وجود داشته باشد. تناظر بین دو مجموعه را با نماد '⇌' نشان داده و مراد از نوشتن A⇌B وجود حداقل یک تابع دو سویی بین A و B است.
توابع را همانطور که در بالا گفته شد ازجمله میتوان با استفاده از یک جدول دو سطری (یا دو ستونی) نمایش داد. در جداول زیر به ترتیب سه تابع t و v ،g تعریف شدهاند.
| g تعریف تابع | g : S ↦ B; S={۰, ۱, ۲, ۳, ۴, ۵}; B={۰, ۱} | |||||
| g(e)∈B | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ |
| g(e)∈B | ۰ | ۱ | ۰ | ۱ | ۰ | ۵ |
تابع g پوشا است ولی یکبهیک نیست | ||||||
| v تعریف تابع | v : B ↦ Σ; B={۰, ۱}; Σ={ ۰, ۲, ۴, . . .} | |
| e∈B | ۰ | ۱ |
| v(e)∈Σ | ۰ | ۱ |
تابع v پوشا نیست ولی یکبهیک است. | ||
| t تعریف تابع | t: B ↦ Γ; B= {۰,۱}; Γ={{۰, ۲, ۴, ... }, {۱, ۳, ۵, ۷, ۹, . . .}} | |
| e∈B | ۰ | ۱ |
| t(e)∈Γ | {۱, ۲, ۴, . . .} | {۱, ۳, ۵, ۷, ۹, . . .} |
| تابع t پوشا و یکبهیک است، لذا بین B و Γ تناظر یکبهیک بهواسطه t برقرار است و میتوان نوشت B⇌Γ. | ||
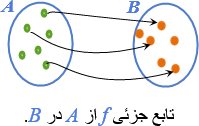
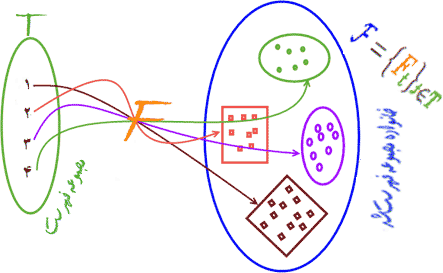
◄ اگر تابع f از S در T پوشا باشد، آنگاه هر زیرمجموعه ناتهی T تصویر یک زیرمجموعه S است.
◄ ازجمله توابع معروف تابع همانی است که برای او قصد هر عزمی خودش است یا بهعبارتدیگر مجموعه آغازی و انجامی آنیکی و تصویر هر عضو، خود آن عضو است (دنیا را از چشم خودش میبیند و نیز در آن فقط خودش را). این تابع را با idS نشان میدهند (S هم مجموعه آغازی و هم انجامی است)، بنابراین idS(x)=x. آشکار است که این تابع یکبهیک و پوشا است و (حتی!) وارون آن نیز خودش است.
◄ تابع معروف دیگر تابع ثابت نام دارد که تصویر هر عضو مجموعه آغازی فقط یک عضو از مجموعه انجامی است(مرغ یک پا دارد). اگر مجموعه آغازی بیش از یک عضو داشته باشد آنگاه این تابع وارون ندارد. اگر این تابع پوشا باشد آنگاه مجموعه انجامی تک عضوی است.
◄ گیریم A و B دو مجموعه؛ مجموعه همه توابع از A در B را با نماد گذاری BA نشان داده.

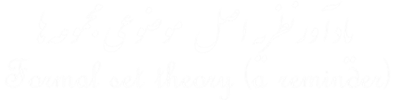



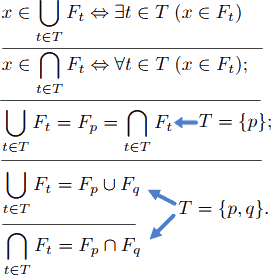
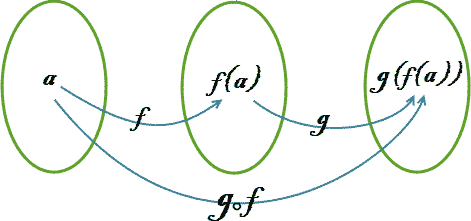
 f
f