مجموعههای متناهی، نامتناهی، شمارا و ناشمارا
یادآور نظریه مجموعهها
درآمد به منطق و رایانش
این قسمت با انگارههای متناهی، نامتناهی، شمارش، شمارشپذیری و شمارشناپذیری آغاز و سر آخر پاسخ به این پرسش که چه شمار متناهی و نامتناهی داریم.
مجموعههای متناهی، نامتناهی، شمارا و ناشمارا
■ داستانک
روزی روزگاری در گذشته یا همین حالا یا در آیندها در یکی از بیشمار جهانها در شهر سایههای بیصاحب که ساکنانش نامیرا بودند؛ فرد آ به فرد ب گفت من عددی طبیعی و بزرگتر از صفر را (n∈ +) را روی کاغذی مینویسم و تو هر روز یک و فقط یک بار آن را گمانهزنی کن و بگو. اگر گمانه تو درست بود من به تو به اندازه شمار
+) را روی کاغذی مینویسم و تو هر روز یک و فقط یک بار آن را گمانهزنی کن و بگو. اگر گمانه تو درست بود من به تو به اندازه شمار  کوه طلا جایزه میدهم. آیا روند کارآمدی هست که اجرای آن فرد ب را به جایزه برسد؟
کوه طلا جایزه میدهم. آیا روند کارآمدی هست که اجرای آن فرد ب را به جایزه برسد؟
برگرفته از: اسمولین۱
■ مجموعههای متناهی و نامتناهی (Finite and infinite sets)

بهطور شهودی میتوان دید  و نیز مجموعه اعداد صحیح، یعنی:
و نیز مجموعه اعداد صحیح، یعنی:
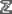 ={. . ., -۳, -۲, -۱, ۰, ۱, ۲, ۳ ,. . .}
={. . ., -۳, -۲, -۱, ۰, ۱, ۲, ۳ ,. . .}
مجموعههای نامتناهی هستند. هدف این بند تعریف دقیق نامتناهی بودن یک مجموعه است. ابتد به مثال زیر توجه نمایید.
مثال: مجموعه اعداد زوج، یعنی {۰, ۲, ۴, ۶, . . .} را E نامیده. روشن است که:
 E ⊂ .
E ⊂ .
نگاشت g از  در E را مطابق جدول زیر تعریف میکنیم.
در E را مطابق جدول زیر تعریف میکنیم.
g :  ↦ E; ↦ E; | تعریف تابع g | ||||||||
| . | . | . | ۵ | ۴ | ۳ | ۲ | ۱ | ۰ | x∈ |
| . | . | . | ۱۰ | ۸ | ۶ | ۴ | ۲ | ۰ | g(x)∈ |
| g(x)=۲x | |||||||||
| تابع g یک تناظر ۱:۱ بین اعداد طبیعی و زیرمجموعه سرهای از آن، یعنی اعداد زوج، برقرار میکند. | |||||||||
ازآنجاکه، برای هر n∈ نظیر آن، ۲n، در E و نیز برای هر عضو e∈E نظیر آن، ۲/e، در
نظیر آن، ۲n، در E و نیز برای هر عضو e∈E نظیر آن، ۲/e، در  وجود دارد، نگاشت g دو سویی است، یعنی بین
وجود دارد، نگاشت g دو سویی است، یعنی بین  و یک زیرمجموعه سره آن، در این مثال E، تناظر ۱:۱ وجود دارد و میتوان نوشت:
و یک زیرمجموعه سره آن، در این مثال E، تناظر ۱:۱ وجود دارد و میتوان نوشت:  ⇌E. بهعبارتدیگر، اعضای
⇌E. بهعبارتدیگر، اعضای  با اعضای زیرمجموعه سرهای از آن جفت شدنی است و این در حالی است که عضوهایی در
با اعضای زیرمجموعه سرهای از آن جفت شدنی است و این در حالی است که عضوهایی در  هست که در E نیست. به گونه دیگر،
هست که در E نیست. به گونه دیگر،  بهعنوان یک کل با جزئی از خود هماندازه است. این ویژگی
بهعنوان یک کل با جزئی از خود هماندازه است. این ویژگی  را نامتناهی بودن
را نامتناهی بودن  نامیده. اگر برای مجموعهای چنین زیرمجموعهای وجود نداشته باشد آنگاه آن مجموعه متناهی است.
نامیده. اگر برای مجموعهای چنین زیرمجموعهای وجود نداشته باشد آنگاه آن مجموعه متناهی است.
■ مجموعه نامتناهی (infinite set)
یک مجموعه را مجموعه نامتناهی گوییم اگر بین آن و زیرمجموعه سرهای از آن، یک تناظر یکبهیک وجود داشته باشد. به مجموعهای که نامتناهی نیست مجموعه متناهی میگویند.
برای مثال هر زیرمجموعه  که دارای بزرگترین عنصر باشد، یا بدانیم اعضای آن از یک عدد طبیعی کوچکترند (دارای کران بالا است)، یک مجموعه متناهی است.
که دارای بزرگترین عنصر باشد، یا بدانیم اعضای آن از یک عدد طبیعی کوچکترند (دارای کران بالا است)، یک مجموعه متناهی است.
☚ یک
مجموعه، به فرض X، نامتناهی است اگر یک تابع یک به یک ولی نه
پوشا از X در
خودش
وجود داشته باشد. برای مثال، f(x)=۲x در  .
.
☚ متمم
زیرمجموعههای متناهی  نامتناهیاند ولی عکس آن همیشه درست نیست.
نامتناهیاند ولی عکس آن همیشه درست نیست.
☚
با استفاده از اصل خوشترتیبی میتوان نشان داد بین هر زیرمجموعه نامتناهی  و خود
و خود  تناظر ۱:۱ برقرار است.
تناظر ۱:۱ برقرار است.
طرح اثبات:
فرض میکنیم A نامتناهی و
A⊂ .
نشان میدهیم ار
.
نشان میدهیم ار
 در A یک نگاشت
دو سویی،
به فرض f، وجود دارد. اکنون به شیوه زیر
f را تعریف
میکنیم:
در A یک نگاشت
دو سویی،
به فرض f، وجود دارد. اکنون به شیوه زیر
f را تعریف
میکنیم:
بنابر اصل خوشترتیبی A دارای کوچکترین عضو است، بنابراین f را به شیوه استقرایی به ترتیب زیر تعریف میکنیم:
A۰= A → f(۰) = least(A), [ ← کوچکترین عضو A least(A)]
A۱= A۰ - {f(۰)} → f(۱) = least(A۱),
.
.
.
An= An-۱ - {f(n - ۱)} → f(n) = least(An).
.
.
.
تابع تعریف شده، یعنی f، یک به یک است. برای دوسویی بودن آن باید نشان دهیم پوشا نیز است.
به شیوه استقرایی داریم:
۰ = least( )
⇒ f(۰) ≥ ۰
)
⇒ f(۰) ≥ ۰
.
.
.
∀n∈ f(n)
≥ n
f(n)
≥ n
⇓
n ∉ Am ⇐ m ≥ n برای هر
⇕ ترانهش:
∃n > m ⇒ n ∈ Am
⇓
f(m) = n

■ شمارایی و کاردینال
میتوان به هر مجموعه متناهی عددی که بهاندازه تعداد اعضای آن مجموعه باشد را نسبت داد و آنها را مقایسه پذیر نمود. آیا مجموعههای نامتناهی نیز مقایسه پذیراند؟ هدف این بند نشان دادن این است که چگونه ریاضیدانان مفهوم مقایسه پذیری را گسترانده تا بهطور عام برای مجموعهها، متناهی و نامتناهی، کار زدنی باشد.
داستان از شمارایی [شمارشپذیری] مجموعهها آغاز میشود. بهطور شهودی، مجموعهای شمارا است که بتوان اعضای آن را توسط اعداد طبیعی فهرست کرد (برشمرد). البته همانطور که خواهیم دید مجموعههایی نیز هستند که شمارا نیستند و اعضای آنها را نمیتوان برشمرد. شمارایی رهنمود ما به مفهوم بینهایت(ها) [اعداد نامتناهی / اعداد بینهایت] و حساب آنها خواهد بود. بنابراین اینک تعریف دقیق شمارایی یک مجموعه را مرور میکنیم.
■ مجموعه شمارا
مجموعه S را یک مجموعه شمارا [یا شمارش پذیر] گویند اگر و فقط اگر
اگر چنین تابعی، به فرض f، باشد، آنگاه میگوییم تابع S ،f را برمیشمرد [برشمردن]. در غیر این صورت میگوییم S یک مجموعه ناشمارا است [برشمردنی نیست].
☚ مجموعههای شمارای نامتناهی در متنهای منطق و ریاضی Denumerable نامیده میشوند.➥
☚ هر مجموعه متناهی شمارا است.
☚ با
توجه به تناظر ۱:۱ اعداد طبیعی و هر زیرمجموعه نامتناهی میتوان گفت: هر زیرمجموعه نامتناهی  شمارا است.
شمارا است.
■ شمارایی اعداد گویا
در جدول زیر اعداد گویای مثبت فهرست شدهاند (برشمرده شدهاند). این نشان میدهد 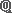 + شمارا است (به همین ترتیب
+ شمارا است (به همین ترتیب 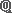 شمارا است و با توجه به
شمارا است و با توجه به  ⊂
⊂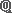 نامتناهی نیز است).
نامتناهی نیز است).
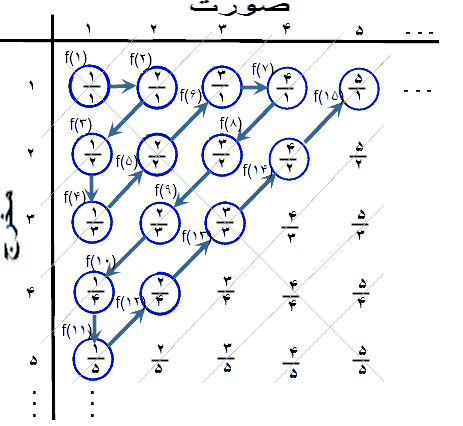
نمودار بالا که نشاندهنده شمارشپذیری اعداد گویا است، همچنین نشان میدهد مجموعه  ×
× شمارا است و میتوان نشان داد که مجموعه همه nتاییهای مرتب اعداد طبیعی نیز شمارایند.
شمارا است و میتوان نشان داد که مجموعه همه nتاییهای مرتب اعداد طبیعی نیز شمارایند.
• تابع جفت سازی استاندارد (Pairing Function)
تابع دو سویی زیر (از  ×
× در
در  )
نیز یک
تناظر یکبهیک بین
)
نیز یک
تناظر یکبهیک بین  ×
× و
و  را تعریف میکند. این تناظر به
تابع جفت سازی استاندارد
معروف است.
را تعریف میکند. این تناظر به
تابع جفت سازی استاندارد
معروف است.
<x, y> = ۱/۲ (x۲ + ۲xy + y۲ + ۳x + y).
بطور کلی با استفاده از این تابع میتوان یک تناظر یک به یک بین
 ۳
و
۳
و  ۲ تعریف کرد. برای نمونه:
۲ تعریف کرد. برای نمونه:
<x, y, z> = <<x, y>, z>.
■ چند خاصیت درباره مجموعههای شمارا
۱- حاصل ضرب دکارتی هر تعداد محدود مجموعه شمارا، شمارا است.
۲- اجتماع هر تعداد محدود مجموعه شمارا، شمارا است.
۳- فرض کنید S یک مجموعه شمارا، آنگاه مجموعه همه زیرمجموعههای متناهی S شمارا است.
۴- مجموعه اعداد جبری شمارا است. [توضیح: عدد حقیقی a را عدد جبری گویند اگر ریشه یک چندجملهای با ضرایب صحیح باشد. نشان داده میشود اعداد گویا جبری هستند ولی همه اعداد حقیقی، برای مثال عدد π و عدد e جبری نیستند. به عدد غیر جبری عدد تراگذری میگویند.]
■ نامحدود مجموعه ناشمارا و نامتناهی وجود دارد.
اثبات:
ابتدا ثابت میکنیم مجموعه توانی  ، یعنی Ƥ(
، یعنی Ƥ( ) ناشمارا و نامتناهی است.
) ناشمارا و نامتناهی است.
Ƥ( ) را Pº مینامیم (به خاطر راحتی در نوشتن).
) را Pº مینامیم (به خاطر راحتی در نوشتن).
روشن است Pº نامتناهی است و بنابراین فقط ثابت میکنیم Pº ناشمارا است.
(توجه داریم که X∈Pº اگر و فقط اگر X⊆ .)
.)
۱- میگوییم، گیریم تابع f :  ↦Pº وجود دارد به قسمی که Pº را برمیشمارد (یعنی Pº شمارا است.)
↦Pº وجود دارد به قسمی که Pº را برمیشمارد (یعنی Pº شمارا است.)
پس برای هر عضو Pº مانند X عدد طبیعی n هست به قسمی که: f(n)∈X.
۲- مجموعه D (D⊆ ) را به قسمی میگیریم که n∈D اگر و فقط اگر n∉f(n).
) را به قسمی میگیریم که n∈D اگر و فقط اگر n∉f(n).
۳- اما ازآنجاکه D∈Pº (چون D⊆ ) و طبق فرض(خلف) f همه
) و طبق فرض(خلف) f همه
اعضای Pº را برمیشمرد پس باید عددی طبیعی مانند d باشد کهf(d)=D.
۴- اما با توجه به ۲ برای هر n∈f(d) ؛n اگر و فقط اگر n∉f(n). و بنابراین بهویژه d∈f(d) اگر و فقط اگر d∉f(d)، که این، یک تناقض و لذا فرض خلف باطل است. بنابراین Pº شمارا نیست و همینطور است برای Ƥ(Ƥº) و ادامه آن.
■ برهان قطری کانتور: مجموعه اعداد حقیقی ناشمارا است (Cantor's diagonal argumentan).

میتوان نشان داد  ناشمارا است. روش اینگونه است که بازه باز (۰,۱) از
ناشمارا است. روش اینگونه است که بازه باز (۰,۱) از  را در نظر گرفته و سپس تابت میکنند برای هر برشمارش این فاصله، عددی در این فاصله است که مشمول برشمارش نخواهد شد. سپس با توجه به اینکه "اگر مجموعهای دارای یک زیرمجموعه سره ناشمارا باشد خود ناشمارا است" نتیجه میگیرند
را در نظر گرفته و سپس تابت میکنند برای هر برشمارش این فاصله، عددی در این فاصله است که مشمول برشمارش نخواهد شد. سپس با توجه به اینکه "اگر مجموعهای دارای یک زیرمجموعه سره ناشمارا باشد خود ناشمارا است" نتیجه میگیرند  ناشمارا است. کانتور به شیوهای موسوم به "برهان قطری کانتور /Cantor's diagonal argumentan" ناشمارایی
ناشمارا است. کانتور به شیوهای موسوم به "برهان قطری کانتور /Cantor's diagonal argumentan" ناشمارایی  را نشان داد. در پایین این برهان آمده است.
را نشان داد. در پایین این برهان آمده است.
مجموعه اعداد حقیقی ناشمارا است.
• برهان:
فرض میکنیم  شمارا است. بنابراین میتوان همه اعداد حقیقی در بازه [۰, ۱) بهعنوان زیر مجموعه
شمارا است. بنابراین میتوان همه اعداد حقیقی در بازه [۰, ۱) بهعنوان زیر مجموعه  برشمرد. نشان میدهیم برای هر برشمارش ممکن این بازه عددی در این بازه هست که در این برشمارش حضور ندارد.
برشمرد. نشان میدهیم برای هر برشمارش ممکن این بازه عددی در این بازه هست که در این برشمارش حضور ندارد.
فرض کنید a۱, a۲, a۳, . . ., an, . . . یک برشمارش این بازه، بفرض توسط تابع f، باشد به قسمی که هر عدد حقیقی در (۰, ۱) دقیقا برای یک (n>۰), n∈ همچون an در این برشمارش آمده باشد (از نوشتن تکرار بیپایان رقم ۹ در نمایش اعشاری خودداری میکنیم؛ برای مثال، بجای ۰/۹۹۹۹ . . . نوشته ۰/۲۰۰۰ . . . )
همچون an در این برشمارش آمده باشد (از نوشتن تکرار بیپایان رقم ۹ در نمایش اعشاری خودداری میکنیم؛ برای مثال، بجای ۰/۹۹۹۹ . . . نوشته ۰/۲۰۰۰ . . . )
اکنون میتوان برشمارش اعداد حقیقی بازه [۰, ۱) را به صورت آرایه زیر نمایاند؛
f(۱)=a۱=۰/a۱۱a۱۲a۱۳a۱۴ . . .
f(۲)=a۲=۰/a۲۱a۲۲a۲۳a۲۴ . . .
f(۳)=a۳=۰/a۳۱a۳۲a۳۳a۳۴ . . .
f(۴)=a۴=۰/a۴۱a۴۲a۴۳a۴۴ . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
که در آن aij یکی از ارقام ۰ تا ۹ باشد. اکنون عدد s=۰/s۱s۲s۳s۴ ... را به شیوه زیر تعریف میکنیم:
s۱ ≠ a۱۱:
برای نمونه ← s۱=۰ وقتی a۱۱≠۰ و s۱=۱ وقتی a۱۱=۰
s۲ ≠ a۲۲:
برای نمونه ← s۲=۰ وقتی a۲۲≠۰ و s۲=۱ وقتی a۲۲=۰
. . .
. . .
si ≠ aii:
برای نمونه ← si=۰ وقتی aii≠۰ و si=۱ وقتی aii=۰ آن)
. . .
. . .
از آنجاکه s در
بازه (۰, ۱) است باید یکی از اعداد برشمرده در
آن بازه باشد. فرض کرده این عدد s=ak باشد. اما این نشدنی است، زیرا رقم
kام s به قرار sk و رقم
kام ak به قرار akk است؛ اما ما sk را نامساوی با akk انتخاب کرده بودیم. بنابراین برشمارش بازه (۰, ۱) نشدنی است و فرض خلاف باطل است؛ یعنی  ناشمارا است.
ناشمارا است.
