برتراند راسل و اصل موضوع انتخاب و انتخاب کفش و جوراب
برای انتخاب یک جوراب از هر یک بی‌نهایت جفت جوراب نیاز به اصل موضوع انتخاب است، ولی برای یک کفش نیاز نیست. — برتراند راسل

■ درباره اصل موضوع انتخاب

نقل قول بالا از راسل در نگاه اول ممکن است به نظر کمی پیچیده بیاید. در زیر می‌کوشیم این نقل قول را واگشایی کنیم.

(آ)- فرض کنید جعبه‌ای دارای نامحدود جفت کفش است. یک مجموعه بسازید که شامل یک کفش از هر جفت باشد.

پاسخ به این قسمت آسان است و کافی است از هر جفت کفش لنگه چپ آن را انتخاب و در مجموعه مورد ساختن قرار دهیم.

(ب)- فرض کنید جعبه‌ای دارای نامحدود جفت جوراب است. یک مجموعه بسازید که شامل یک جوراب از هر جفت باشد.

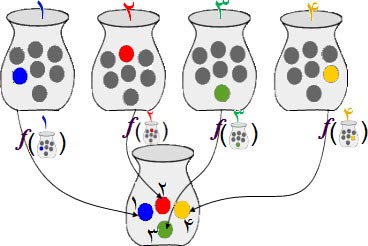
پاسخ به این قسمت هرگز آسان نیست زیرا هیچ قاعده طبیعی (نگاشت) برای انتخاب یک جوراب از هر جفت جوراب (خلاف انتخاب یک لنگه کفش از یک جفت کفش) وجود ندارد. فرض کنید مجموعه‌ نامتناهی داریم که هر عضو آن خود مجموعه‌ای دو عضوی است. در واقع و نزدیک‌تر به زبان ریاضی، این پرسش می‌خواهد بداند آیا مجموعه S وجود دارد که شامل یک عنصر از هر یک از مجموعه‌های دو عضوی باشد؟ بعبارت دیگر، آیا مجموعه S وجود دارد که شامل یک عنصر از هر یک از مجموعه نامتناهی از مجموعه‌های دو عضوی باشد؟

نکته بسیار مهم و در ظاهر شگفت این است که قبول وجود مجموعه بند (ب)، بعبارت دیگر پذیرش تابع انتخاب برای گزینش لنگه جوراب‌ها، یا عدم قبول آن موجب هیچ ناسازگاری در بنای نظریه مجموعه‌ها (و ریاضیات جاری) نمی‌شود. (در یادداشت‌های منطق خواهیم دید که اگر فرمولی در یک دستگاه اصل موضوعی (منطق کلاسیک) که سازگار است قضیه نباشد آنگاه نقیض آن‌ را می‌توان بدون خدشه به سازگاری به اصول موضوعه دستگاه افزود.)

■ اصل موضوع انتخاب

اصل موضوع انتخاب، با کوته نویسیِ(Axiom of Choice) AC توسط منطقی و ریاضیدان آلمانی ارتست زیملو ارائه گردیده. طبق این اصل اگر اعضای کلاسی، به فرض C، مجموعه‌های ناتهی باشند، آنگاه مجموعه‌ای هست که با هر یک از اعضای این کلاس دقیقاً یک عضو مشترک داشته باشد.

■ تابع انتخاب

گیریم کلاس C به قرار زیر باشد:

C = {X|X یک مجموعه ناتهی}

برای مثال C می‌تواند {X|X ∈ Ƥ(R)} یا {{۱, ۲}, {۲, ۵, ۷}} و مانند آن‌ها باشد.

اصل موضوع انتخاب می‌گوید فرض وجود C منجر به وجود تابعی، به فرض f، از C در مجموعه‌ای، به فرض Z، می‌گردد، به قسمی که، هر عضو Z انتخاب‌شده (‌دست‌آمده) توسط تابع f از عضوهای C است. یعنی، برای هر X∈C داریم:

f(X)=z∈X؛ (z∈Z). تابع f را تابع انتخاب می‌نامند.

اصل موضوع و تابع انتخاب
وقتی اعضای C مجموعه‌های متناهی باشند اصل موضوع انتخاب بدیهی و تابع انتخاب نیز محاسبه پذیر است. اما وقتی آن‌ها نامتناهی باشند غموض آشکار می‌شود.

درباره AC باید دانست:

۱- از اصل انتخاب به دست نمی‌آید چه گونه می‌توان تابع انتخاب را ساخت (محاسبه کرد) و بنابراین ناساختی (non-constructive) است. این اصل فقط مدعی وجود چنین تابعی است؛

۲- چنانچه C متناهی باشد می‌توان نشان‌ داد تابع انتخاب وجود دارد و بنابراین در این حالت وجود تابع انتخاب موکول به پذیرش اصل موضوع انتخاب نیست؛

۳- از اصل انتخاب می‌توان نتیجه گرفت که هر مجموعه خوش‌-ترتیب شدنی است (ولی نمی‌گوید چگونه باید آن را خوش-ترتیب کرد.) این نتیجه به قضیه خوش-ترتیبی [همچنین به قضیه زیملو] معروف است.

۴- هم‌ارزی اصل انتخاب و قضیه خوش-ترتیبی: از قضیه خوش-ترتیبی می‌توان اصل موضوع انتخاب را به دست آورد. به عبارت دیگر، این دو (خوش-ترتیب شدن و انتخاب کردن) هم‌ارز هستند. یعنی:

قضیه خوش-ترتیبی ⇔ اصل موضوع انتخاب

۵- گونه ضعیف‌تر AC موسوم به اصل موضوع انتخاب وابسته با ادعای کمتر می‌گوید مجموعه‌های شمارا دارای تابع انتخاب هستند.

☚ قضیه خوش-ترتیبی، شماره ۳ در بالا، متفاوت از اصل خوش‌ترتیبی است.

☚ در قسمت بعد به اصل موضوع انتخاب بر خواهیم گشت و بیشتر درباره آن صحبت می‌کنیم.

■ مثال کاربرد اصل موضوع انتخاب

فرض کنید g یک تابع پوشا از Y در X باشد. نشان دهید یک تابع یک‌به‌یک، بفرض f، از X در Y وجود دارد.

گیریم F یک تابع از X در P(Y) (مجموعه توانی‌ Y) باشد، به قسمی که:

F(x) = {y ∈ Y : g(y) = x}.

از آنجاکه g پوشا است برای هر x∈X داریم F(x)≠Ø. اکنون فرض کنید f یک تابع انتخاب (که بنا به اصل موضوع انتخاب وجود دارد) از X در Y برای F باشد. بنابراین برای هر x ∈ X داریم:

f(x) ∈ F(x) ⊆ Y.

بنابراین f یک تابع از X در Y است. اکنون می‌توان گفت اگر x۱=x۲ آنگاه F(x۱) و F(x۲) ازهم جدا هستند. و از اینجاf(x۱)≠f(x۲) . بنابراین f یک به یک است.