مربع سنتی تقابل
گزارههای حملی (منطق قیاسی)
درآمد به منطق فصل ۶ قسمت ۵
در
قسمت
پیشین دیدیم یک گزاره حملی استاندارد-ساخت دارای سه ویژگی
بنیادی است: ۱- کیفیت
[نشان دهنده ایجابی (پذیرشی) یا سلبی
(ناپذیرشی) بودن آن]
۲- کمیت
[نشان
دهنده کلی (فراگیر) یا جزيی
(بخشی) بودن آن] ۳- توزیعشدگی
(نشان دهنده چگونگی برشمارش
حدود
خود).
در این قسمت درباره آنچه موسوم به تقابل دو گزاره حملی نسبت به هم است میگوییم.
و اینکه، دو گزاره حملی میتوانند
متناقض، متضاد یا
متضاد فرعی (داخل در تضاد) و مانند اینها باشند.
مربع تقابل نموداری است که این روابط را آشکار و نمایش میدهد.
افزون بر این، استنتاجهای بیواسطه که از مربع تقابل برمیآیند را هم خواهیم دید.
۵.۶ مربع سنتی تقابل
تقابل
Opposi-tion
رابطهای منطقی که بین دو متناقض، بین دو متضاد، یا بطور کلی بین هر دو گزاره حملی که در کیفیت، کمیت، یا جهات دیگر متفاوتاند وجود دارد. این روابط در مربع تقابل نمایش داده میشوند.
متناقضها
Contrad-ictories
دو گزاره مرتبط آنگونه که یکی انکار یا نقض دیگری باشد. در مربع تقابل
سنتی، دو زوج گزاره متناقض بوسیله قطرهای مربع نشان داده میشوند:
A و E به ترتیب متناقضهای
O و I هستند.
متضادها
Contraries
دو گزاره مرتبط آنگونه که نتوانند هر دو درست باشند، گرچه ممکن باشد هر دو نادرست باشند.
داخل در تحت تضاد
Subcont-raries
دو گزاره آنگونه مرتبط که نتوانند هر دو نادرست باشند، گرچه ممکن باشد هر دو درست باشند.
تداخل
Subalter-nation
رابطه موجود در مربع تقابل
سنتی بین یک گزاره کلی
(یک A یا یک E)
و گزاره جزئی نظیر آن
(به ترتیب، یک I یا یک O).
در رابطه تداخل، گزاره جزئی (I یا O) متداخل محاطی
(sub-altern)
و گزاره کلی (A یا E) متداخل محیطی
(super-altern)
نامیده میشوند.
مربع تقابل
Square of opposition
یک نمودار مربعی و نمایشدهنده روابط منطقی (موسوم به «تقابلها») بین چهار گونه گزاره حملی (A، I، E و O) که در چهارگوشه آن قرار دارند.
استناج بیواسطه
Immediate inference
یک اندیافت که مستقیماً از یک مقدمه و بدون واسطهیِ هر مقدمه دیگر دست آمده باشد.
اقسام گوناگون استنتاجهای بیواسطه را میتوان تمیز داد، که بگونه سنتی شامل:
۱- عکس مستوی (Convers-ion)،
۲- عکس متمم (Obvers-ion)
۳- وعکس نقیض (Contraposi-tion) هست.
■ تقابل
تحلیل گزارههای حملی در قسمتهای قبلی ما را به نمایاندن روابط بین این گزارهها توانا میسازد، که این به سهم خود پایه استواری برای بسیاری استدلالها، که در زندگی روزانه انجام میدهیم، فراهم میآورد. در ادامه نیاز است تا با عبارت فنی دیگر موسوم به تقابل آشنا شویم. توضیح آنکه؛ گزارههای حملی استاندارد-ساخت با حدود موضوع و محمول یکسان میتوانند در کیفیت یا کمیت و یا هردو متفاوت باشند. به هرگونه از این تفاوتها بهطور سنتی تقابل میگویند. این عبارت حتی وقتی اختلاف آشکاری هم بین گزارهها نیست بهکاربرده میشود. انواع مختلف تقابل (که در ادامه خواهیم دید) با بعضی روابط بسیار مهم صدق(درستی / نادرستی گزارهها) همبسته است.
آ. متناقضها:
دو گزاره متناقض هستند هرگاه یکی انکار یا نقض دیگری باشد— بهعبارتدیگر، آنها نتوانند هردو باهم درست و هردو باهم نادرست باشند. دو گزاره حملی استاندارد-ساخت که دارای حد موضوع و حد محمول یکسان، ولی در کمیت و نیز در کیفیت (در هردو) متفاوتاند، متناقضاند.
بنابراین گزاره A "همه قضات وکیل هستند" و گزاره O "برخی قضات وکیل نیستند" آشکارا متناقض هستند. آنها هم در کیفیت (یکی پذیرشی و دیگری ناپذیرشی است) و هم در کمیت (یکی به همه و دیگری به بعضی اشاره دارد) متفاوت هستند. از این دو دقیقاً یکی درست و دقیقاً یکی نادرست است. آنها هردو نمیتوانند درست باشند؛ و نیز هردو نمیتوانند نادرست باشند.
به همین شیوه گزاره E "هیچ سیاستمداری آرمانگرا نیست" و گزاره I "بعضی سیاستمداران آرمانگرا هستند"، هردو در کیفیت و کمیت در تقابل و متناقض نیز هستند.
بهطور خلاصه: گزارههای A و O متناقض هستند. گزاره "بعضی P S نیست" گزاره "همه P S است" را نقض میکند. گزارههای E و I نیز متناقض هستند: گزاره "بعضی P S است" گزاره "هیچ P S نیست" را نقض میکند.
ب متضادها:
دو گزاره متضاد هستند اگر هردو نتوانند درست باشند— بهعبارتدیگر، هرگاه درستی یکی مستلزم نادرستی دیگری باشد. بنابراین "تیم خوزستان در بازی آینده تیم خراسان را خواهد برد" و گزاره "تیم خراسان در بازی آینده تیم خوزستان را خواهد برد" متضاد هستند. اگر یکی از این دو گزاره (که البته به یک بازی یکسان اشاره دارند) درست باشد، آنگاه دیگری باید نادرست باشد. اما این دو نقیض یکدیگر نیستند، زیرا ممکن است این دو تیم در قرعهکشی مقابل هم قرار نگیرند. متضادها نمیتوانند هر دو درست باشند اما خلاف متناقضها هر دو میتوانند ممکنن نادرست باشند.
مطابق با برآورد سنتی از گزارههای حملی، گزارههای کلی (A و E) که دارای موضوع و محمول یکسان هستند، ولی در کیفیت (یکی پذیرشی و دیگری ناپذیرشی) متفاوتاند، گزارههای متضاد هستند. ازاینرو گفتهشده میتوان یک گزاره A "همه شاعران رؤیاپرداز هستند" و گزاره نظیر E آن "هیچ شاعر رؤیاپرداز نیست" که نمیتوانند هر دو درست باشند– لیکن هردو میتوانند نادرست باشند را بهعنوان متضاد در نظر گرفت. این تفسیر ارسطویی دارای برخی پیامدهای مسئلهساز است و ما در قسمت ۷ همین فصل بهتفصیل درباره آنها بحث خواهیم کرد.
یکی از مشکلات برخاسته از این تفسیر ارسطویی این است که اگر هریک از گزارههای A یا E ضرورتاً درست باشد– یعنی درستی منطقی یا ریاضی داشته، مثل "همه مربعها مستطیل هستند" یا "هیچ مربع دایره نیست"، آنگاه در این حالت ادعای اینکه A و E متضاد هستند نمیتواند درست باشد، زیرا هیچ گزارهای با درستی ضروری نمیتواند به امکان نادرست باشد.
گزارههایی که نه بگونه ضروری درست و نه بگونه ضروری نادرست هستند،گزارههای ممکن نام دارند. بنابراین، پاسخ این مشکل این است که فرض شود (که فرض نامعقولی نیست) گزارههای موردنظر ممکن هستند، و آنگاه با این تعبیر ادعای اینکه گزارههای A و E با حد موضوع و حد محمول یکسان متضاد هستند میتواند درست باشد. در باقیمانده این فصل فرض بر این خواهد بود که گزارههای موردنظر ممکن هستند.
ج. داخل در تحت تضاد:
دو گزاره را داخل در تحت تضاد گویند اگر هردو نتوانند نادرست باشند، گرچه ممکن است هردو درست باشند.
بنا بر تفسیر سنتی، گزارههای جزئی (I و O)، که دارای حدهای موضوع و محمول یکسان ولی در کیفیت متفاوتاند (یکی پذیرشی و دیگری ناپذیرشی)، داخل در تحت تضاد هستند. گفتهشده، گزاره I "بعضی الماسها سنگهای گرانبها هستند"، و گزاره O "بعضی الماسها سنگهای گرانبها نیستند"، میتوانند هردو درست باشند— اما نمیتوانند هردو نادرست باشند و بنابراین باید آنها را داخل در تحت تضاد در نظر گرفت.
مشکل مشابه با آنچه در بالا دیدیم اینجا نیز نمایان میگردد. اگر هریک از گزارههای I یا O به گونه ضروری نادرست باشند (برای مثال "بعضی مربعها دایره هستند” یا "بعضی مربعها مستطیل نیستند")، آنگاه نمیتوانند داخل در تحت تضاد باشند، زیرا دو گزاره داخل در تحت تضاد میتوانند هردو درست باشند. اما اگر هر دو گزاره I و O گزارههای ممکن باشند آنگاه هردو میتوانند درست باشند و بنابراین، همانگونه که در بالا و در رابطه با تضاد دیدیم، در باقیمانده این فصل فرض بر این خواهد بود که گزارههای موردنظر ممکن هستند.
د. تداخل:
گزارههای متناظر: هرگاه دو گزاره در حد موضوع و حد محمول یکسان و در کیفیت نیز یکسان باشند (هردو پذیرشی یا هردو ناپذیرشی) ولی در کمیت متفاوت باشند (یکی کلی و دیگر جزئی)، آنان را دو گزاره متناظر گویند.
این نیز آنگونه که بهطور سنتی بهکاربرده میشود صورتی از تقابل است. بنابراین گزاره A "همه عنکبوتان حیوانات هشتپا هستند" دارای گزاره نظیر I "بعضی عنکبوتان حیوانات هشتپا هستند” خواهد بود. به همین ترتیب گزاره E "هیچ نهنگی ماهی نیست" دارای گزاره نظیر O "بعضی نهنگها ماهی نیستند،" خواهد بود. این تقابل بین گزارههای کلی و گزارههای متناظر جزئی آنها تداخل نامیده شده است. در هر زوج از گزارههای نظیر، گزاره کلی را متداخل محیطی و گزاره جزئی را متداخل محاطی مینامند.
در تداخل (بنا بر تحلیل سنتی) از تداخل محیطی درستی تداخل محاطی نتیجه میشود. بنابراین از گزاره موجب کلی، "همه پرندگان پردار هستند،” گزاره نظیر موجب جزئی، "بعضی پرندگان پردار هستند" نتیجه میشود. از گزاره سالب کلی "هیچ نهنگی ماهی نیست،" به همین ترتیب جزئی نظیر آن "بعضی نهنگها ماهی نیستند" به دست میآید. اما، این نتیجهگیری از جزئی به کلی حاصل نمیشود. از گزاره "بعضی حیوانات گربه هستند،" آشکار است که نمیتوان نتیجه گرفت "همه حیوانات گربه هستند" و همینطور مهمل خواهد بود اگر از "بعضی حیوانات گربه نیستند" نتیجه بگیریم "هیچ حیوانی گربه نیست".

ه. مربع تقابل:
به چهار طریق گزارهها میتوانند در تقابل باشند— بهعنوان تناقض، تضاد، داخل در تحت تضاد و بهعنوان تداخل (محاطی و محیطی). آنها توسط یک نمودار مهم و بسیار مورد کاربرد بنام مربع تقابل نمایش داده میشوند. این نمودار در شکل ۱-۶ نمایش داده شده است:
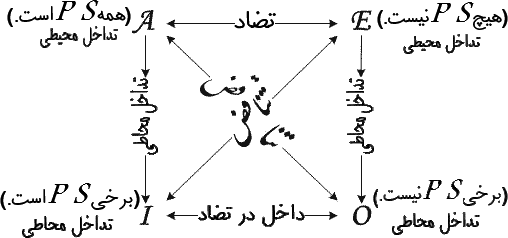
عقیده بر آن بود که روابط نشان داده در مربع تقابل مبنایی جهت اعتبار شکلهای مقدماتی و خاص از استدلال هستند. برای توضیح آنها ابتدا باید استنتاج بیواسطه و استنتاج بهواسطه را از هم تمیز دهیم.
وقتی نتیجهای را از یک یا تعداد بیشتر مقدمه استخراج میکنیم، آنگاه میباید استنتاجی حضور داشته باشد. هرگاه پای بیش از یک مقدمه در میان باشد این استنتاج را بهواسطه میگویند، زیرا نتیجه از مقدمه اول و بهواسطه مقدمه دوم بهدستآمده است. اما وقتی نتیجه فقط از یک مقدمه حاصل آمده باشد، آنگاه پای چنین واسطهای در میان نخواهد بود، و در این حالت آن را استنتاج بیواسطه میگویند.
تعدادی از استنتاجهای بیواسطه و بسیار مفید را میتوان از اطلاعات جای یافته در مربع تقابل به دست آورد. در زیر مثالهایی آمده است.
اگر گزاره A مقدمه ما باشد، آنگاه (مطابق با مربع تقابل) به گونه معتبر میتوان به دست آورد که گزاره نظیر آن (یعنی گزاره O با حد موضوع و حد محمول یکسان) نادرست است.
اگر گزاره A مقدمه ما باشد، گزاره نظیر I آن درست است.
اگر I گزاره مقدمه باشد، گزاره نظیر E آن، که نقیض آن است، باید نادرست باشد.
با فرض درستی یا نادرستی یکی از گزارههای حملی استاندارد-ساخت، درستی یا نادرستی بعضی یا همه سه گزاره دیگر بیواسطه استنتاج خواهد شد. تعداد قابلملاحظهای استنتاج بیواسطه بر مبنای جدول تقابل سنتی قابلاستخراج است، که در زیر آنها را نشان دادهایم.
| A درست فرض شده باشد. | E نادرست، I درست، O نادرست است. | |
| E درست فرض شده باشد. | A نادرست، I درست، O نادرست است. | |
| I درست فرض شده باشد. | E نادرست است، A و O نامعین هستند. | |
| O درست فرض شده باشد. | A نادرست است، E و I نامعین هستند. | |
| A نادرست فرض شده باشد. | O درست است، E و I نامعین هستند. | |
| E نادرست فرض شده باشد. | I درست است، A و O نامعین هستند. | |
| I نادرست فرض شده باشد. | A نادرست، E درست، O درست است. | |
| O نادرست فرض شده باشد. | A درست، E نادرست، I درست است.* | |
*- یک گزاره نامعین است اگر درستی یا نادرستی آن با درستی یا نادرستی گزاره دیگری معین نشود. به تعبیری دیگر، یک گزاره نامعین است اگ دانسته نباشد که درست است و همچنین دانسته نباشد که نادرست است. اگر فرض شود که گزاره A نامعین است، به هر دو تعبیر، میتوان استنباط کرد که گزاره نقیض آن O باید به همان تعبیر نامعین باشد. زیرا اگر دانسته بود گزاره O درست بوده، گزاره A که با آن متناقض بود نادرست میبود. و اگر دانسته بود گزاره O نادرست بوده، گزاره A که با آن متناقض است درست میبود. همین استدلال در مورد دیگر گزارههای استاندارد-ساخت نیز نیز برقرار است. اگر هر یک از گزارههای چهارگانه حملی بهعنوان نامعین داده شوند، متناقض آن باید به همان معنا نامعین باشد. | ||
تمرین
در تمرینات زیر (۱) چنانچه در هر دسته، گزاره اول را درست فرض کنیم آنگاه درباره درستی / نادرستی بقیه چه میتوان گفت؟ (۲)چنانچه در هر دسته، گزاره اول را نادرست فرض کنیم آنگاه درباره درستی / نادرستی بقیه چه میتوان گفت؟
۱:
آ-همه مدیران موفق آدم روشنبین هستند.
ب-هیچ مدیر موفق آدم روشنبین نیست.
ج-برخی مدیران موفق آدم روشنبین هستند.
د-بعضی مدیران موفق آدم روشنبین نیستند.
حل ۱:
اگر گزاره (آ) درست فرض شود آنگاه:
(ب) متضاد و درست است،
(ج) متداخل محاطی و درست است،
(د) متناقض و نادرست است.
اگر گزاره (آ) نادرست فرض شود آنگاه:
(ب) متضاد و نامعین است،
(ج)متداخل محاطی و نامعین است،
(د) متناقض و درست است.
۲:
آ – هیچ حیوان شاخدار گوشتخوار نیست.
ب - بعضی حیوانات شاخدار گوشتخوار هستند.
ج – بعضی حیوانات شاخدار گوشتخوار نیستند.
د – همه حیوانات شاخدار گوشتخوار هستند.
۳:
آ – بعضی ایزوتوپهای اورانیوم عنصر بسیار ناپایدار هستند.
ب – بعضی ایزوتوپهای اورانیوم عنصر بسیار ناپایدار نیستند.
ج – همه ایزوتوپهای اورانیوم عنصر بسیار ناپایدار هستند.
د – هیچ ایزوتوپ اورانیم عنصر بسیار ناپایدار نیست.
۴:
آ – بعضی اساتید کالج مدرس دلپذیر هستند.
ب – همه اساتید کالج مدرس دلپذیر هستند.
ج – هیچ استاد کالج مدرس دلپذیر نیست.
■ ■ ■ ■ ■
