برگردان گزارههای حملی به صورت استاندارد
قیاس در سخن
درآمد به منطق فصل ۸ قسمت ۳
در قسمت قبل به الگوی انحراف دوم، یعنی حضور بیش از سه حد در استدلال قیاسی، و برگردان آن به ساختِ استاندارد بوسیله حذف حدهای مترادف و متمم پرداختیم. این قسمت به الگوی انحراف سوم، یعنی وقتی مقدمات قیاس به ساخت استاندارد نیستند میپرازد و ۹ ساخت گزارهای در زبان عادی را شناسایی و روشهای کارآمدی برای برای کاهش آنها ارایه میدهد.
۸.۳ برگردان گزارههای حملی به صورت استاندارد
گزاره تکینه
گزاره شخصیه
Singular proposition
گزاره که مدعی است یک تک-شئ دارای (یا نادارای) بعضی ویژگیهای مشخص است.
گزاره ویژهساز
گزاره حصری
Exclusive propositions
گزارهای که مدعیاست محمول انحصاراً به حد موضوع نسبت داده شده.
مثال:
«هیچکس مگر ژنرالها ستاره نشان هستند»
مدعی است که محمول «ستاره نشان» فقط به موضوع، یعنی ژنرالها، حمل میشود.
گزاره استثناساز
گزاره جداساز
Exceptive Proposition
گزارهای که مدعی است همه اعضای بعض کلاس، بهاستثنای اعضای یکی از زیرکلاسهایش عضو کلاس دیگری هستند.
گزارههای استثناساز در واقعیت گزاره مرکب هستند، زیرا آنها مدعی یک رابطه شمول و یک رابطه عدم شمول هستند.
مثال:
«همه افراد بهجز کارمندان حائز شرایط هستند»
یک گزاره استثناساز است که در آن، هم "همه غیرکارمندان حائز شرایط هستند" و هم "هیچ کارمند حائز شرایط نیست" ادعاشده است.
در قسمت یکم این فصل آمد که استدلالهای قیاسی در زبان عادی ممکن است از قیاسهای حملی استاندارد-ساخت منحرف شوند و این نهتنها بخاطر آن باشد که در آنها ممکن است به نظر برسد دارای بیش از سه حد هستند (بحث شده انحراف یافتگی دوم)، بلکه افزون بر آن، گزارههای تشکیلدهنده یک قیاس در زبان عادی ممکن هست همه گزاره حملی استاندارد-ساخت نباشند. گزارههای A، E، I و O تا اندازهای دستساز جلوه میکنند و بسیاری از استدلالهای قیاسی در زبان عادی شامل گزارههای غیراستاندارد-ساخت هستند. برای برگردان (کاهش) این استدلالها به ساختهای استاندارد نیاز است تا گزارههای بکاررفته در استدلال به صورت استاندارد برگردان شوند.
اگر فهرستی مرتب از قواعد مشخص وجود داشت تا با کارزدن آنها بتوان این برگردانها را انجام داد، کار بسیار آسان بود. اما زبان عادی بیشتر از آن غنی و چندساحتی است تا بتوان تعدادی قاعده برای اینچنین برگردانی فراهم آورد. انواع مختلف برگردان برای چینشهای مختلف موردنیاز است. در هر حالت آنچه بسیار اهمیت دارد توانایی در فهم گزارههای غیراستاندارد-ساخت است و اینکه چگونه میتوان بدون کاستی در معنا، آنها را بهصورت استاندارد پیکربندی کرد.
گرچه مجموعه کاملی از قواعد را نمیتوان به دست داد، میتوان چند روش به خوبی آزمون شده را برای برگردان گزارههای غیراستاندارد از گونههای مختلف ارائه کرد. این روشها— که ۹ شمار از آنها در این قسمت میآید— را باید همچون راهنما، بجای قاعده، در نظر داشت؛ اینها تکنیکهایی هستند که میتوان با آنها گزارههای غیراستاندارد از گونههای قابلشرح معینی را به گزارههایی به ساخت استاندارد برگرداند آنگونه که بعنوان مؤلفههای سازنده استدلالهای قیاسی به کار آیند.
آ- گزارههای تکینه (شخصیه)
بعضی گزارهها تصدیق یا انکار میکنند که یک فرد یا شئ معین متعلق به یک طبقه (کلاس) دادهشده است— برای مثال، «سقراط یک فیلسوف است» یا «این میز عتیقه نیست.» به این گزارهها گزارههای تکینه (نیز: گزارههای شخصیه) گفته میشود. این گزارهها به تأیید یا انکار شمولیت یک کلاس در کلاس دیگر نپرداخته (آنچه گزاره حملی استاندارد-ساخت انجام میدهد)، بااینوجود، میتوان یک گزاره تکینه را همچون یک گزاره درباره طبقهها (کلاسها) و روابط بین آنها تعبیر کرد. ما این کار را مطابق با آنچه به دنبال میآید انجام خواهیم داد.
به هر شئ انفرادی یک کلاس یکتایی یگانه نظیر میگردد که تنها عضو آن خود شئِ انفرادی است. اکنون، ادعای اینکه شئ s متعلق به طبقه P است منطقاً همارز با این ادعا است که طبقه یکتایی S، شامل شئ s، بهتمامی مشمول طبقه P است. بعلاوه، ادعای اینکه شئ s متعلق به طبقه P نیست منطقاً همارز با این ادعا است که طبقه یکتایی S، شامل شئ s، بهتمامی مستثنا از طبقه P است.
معمول چنین است که این تعبیر بهخودیخود و بدون هرگونه تنظیم نشانهگذاری انجام پذیرد. بنابراین، هر گزاره موجب تکینه بهصورت «P s است» را اینگونه در نظر گرفته که همچون یک پیکربندی جایگزین برای گزارهیِ منطقاً همارز A «همه P - S است» بیانشده است. و به همین روش، هر گزاره سالب تکینه «P s نیست» را اینگونه در نظر گرفته که همچون یک پیکربندی جایگزین برای گزارهیِ منطقاً همارز E «هیچ P - S نیست» بیان شده است— در هر دو حالت، S بعنوان مشخصکننده طبقه یگانهای که تنها عضو آن شئ s است فهمیده میشود. بنابراین هیچ برگردان صریحی برای گزارههای تکینه در نظر گرفته نشده است، و بهطور سنتی آنها را بعنوان گزارههای A و E همانگونه که هستند طبقهبندی کردهاند. همانطور که کانت خاطرنشان کرد "برای منطقدانها توجیهپذیر است تا برای داوری در امر قیاس، گزارههای تکینه را مطابق با گزارههای کلی در نظر بگیرند[۱].
[۱]. امانوئل کانت. نقد عقل منطق، ۱۷۸۱، مفاهیم تحلیلی، فصل اول، بخش دوم.
بیشتر از یک قرن بعد برتراند راسل تعبیری را کاملاً متفاوت از گزارههای شخصیه و گزارههای حملی کلی (A و E) ارائه داد. وی بعد (در My Philosophy Development) استدلال کرد که تا وقتی منطق این دو صورت را بهتمامی متفاوت از هم نبیند «نمیتواند جلوتر برود»، زیرا یکی (تکینه) یک محمول را به یک موضوع نامداده شده نسبت میدهد، حالآنکه دیگری (کلیه) رابطهيِ بین دو محمول را بیان میکند. تعبیر راسل در آن زمان در نظریه سورها در منطق جدید جنبه مرکزی یافت، که در فصل ۱۱ بالنسبه مفصل موردبحث قرار خواهد گرفت. بررسی کانت مربوط به کاربرد گزارههای شخصیه در قیاسهای سنتی بود، که وی میاندیشید آنها باید ابزارهای منطقی بسیار توانمند باشند.
اما داستان به این سادگی نیست. بخاطر دارید که گزارههای جزئی (I و O) دارای نهاده وجودی بودند و گزارههای کلی (A و E) فاقد نهاده وجودی بودند. با به کار گرفتن تعبیر بولی، اگر با گزارههای تکینه همچون گزارههای A و E در استدلالهای قیاسی رفتار کنیم درمییابیم آزمون اعتبار آنها بهوسیله نمودارهای ون یا قواعد قیاسی مشکلات جدی پیش خواهد آورد.
در بعضی حالات یک استدلال دو مقدمهای که شامل گزاره تکینه است و آشکارا معتبر است به یک قیاس حملی معتبر برگردانده میشود، برای مثال:
| همه M - H است. s یک H است. ∴ s یک M است. | به قیاس معتبر حملی AAA-۱ (باربارا) برگردان میشود، | همه M - H است. همه H - S است. ∴ همه M - S است. |
اما در بعضی حالات دیگر برگردان یک استدلال قیاسی با دو مقدمه که شامل گزاره تکینه است و آشکارا معتبر است، منتج به قیاس حملی نامعتبر خواهد شد، برای مثال:
| s یک M است. s یک H است. ∴ بعضی M - H است. | به قیاس نامعتبر حملی AAI-۳ برگردان میشود، | همه M - S است. همه H - S است. ∴ بعضی M - H است. |
این قیاس مرتکب مغالطه وجودی شده و قاعده ۶ را رعایت نکرده.
از سوی دیگر اگر گزاره تکینه را به گزاره جزئی (I یا O) برگردانیم، مانند این مشکل بازهم وجود خواهد داشت، در بعضی حالات یک استدلال دو مقدمهای که شامل گزاره تکینه و آشکارا معتبر است به یک قیاس حملی معتبر برگردانده میشود، برای مثال:
| همه M - H است. s یک H است. ∴ s یک M است. | به قیاس معتبر حملی AII-۱ (دری) برگردان میشود، | همه M - H است. بعضی H - S است. ∴ بعضی M - S است. |
اما در بعضی حالات دیگر، استدلالهای آشکارا معتبر با دو مقدمه که دارای گزاره تکینه هستند به یک قیاس حملی نامعتبر برگردانده میشوند، برای مثال:
| s یک M است. s یک H است. ∴ بعضی M - H است. | به قیاس نامعتبر حملی III-۳ برگردان میشود، | بعضی M - S است. بعضی H - S است. ∴ بعضی M - H است. |
که مرتکب مغالطه توزیعنشدگی حد وسط است، و قاعده ۲ را رعایت نکرده.
مشکل برخاسته از این واقعیت است که، یک گزاره تکینه شامل اطلاعات بیشتری از هریک از ۴ صورت گزارههای حملی استاندارد-ساخت است. اگر ساختار "P s است" مثل "همه P - S است" باشد، چیزی که از بین میرود نهاده وجودی گزاره تکینه است، یعنی این واقعیت که S خالی نیست. اما اگر ساختار "P s است" مثل "بعضی P - S است" باشد، چیزی که از دست میرود جنبهکلی گزاره تکینه است، که حد موضوع خود را توزیع میکند، یعنی این واقعیت که همه P - S است.
حل این مشکل بهاینترتیب است که گزاره تکینه ترکیب عطفی گزارههای حملی استاندارد-ساخت باشد. یعنی، یک گزاره موجب تکینه با ترکیب عطفی گزارههای حملی مربوط، یعنی A و I همارز باشد. بنابراین، گزاره "P s است" همارز است با یک گزاره کلی "همه P - S است" و یک گزاره جزئی "بعضی P S است". بههمین ترتیب، یک گزاره سالب تکینه با عطف گزارههای حملی E و O همارز است. بنابراین، گزاره "P s نیست" همارز است با یک گزاره کلی "همه P - S نیست" و یک گزاره جزئی "بعضی P S نیست."
نمودارهای ون برای گزارههای موجب و سالب تکینه در شکل ۱ نمایش دادهشده است.
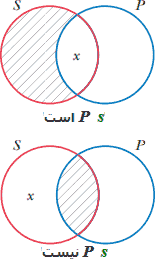
در کاربرد قواعد قیاس برای برآورد استدلالهای قیاسی که شامل گزارههای تکینه هستند، باید همه اطلاعات موجود در گزاره تکینه، یعنی هم جنبه توزیعشدگی و هم جنبه وجودی، آنها بهحساب گرفته شود.
بهشرط آنکه جنبه وجودی گزارههای تکینه را به یاد داشته باشیم، آنگاه میتوان در بررسی اعتبار استدلالهای قیاسی، از نمودارهای ون یا قواعد قیاسهای حملی استفاده کرد. در این صورت و در عمل پذیرفته است تا به گزارههای تکینه همچون گزارههای حملی (A و E) نگریسته شود.
ب- گزارههای حملی که در آنها بجای بکاربردن عبارت یا نام برای مشخص کردن یک کلاس، صفت یا عبارت وصفی بکار رفته.
برای مثال گزارههای «بعضی گلها زیبا هستند» یا «هیچ کشتی جنگی آماده انجاموظیفه نیست» باید به گزارههای حملی استاندارد برگردانده شوند. انحراف آنها از صورت استاندارد در این است که محمول «زیبا» و «آماده انجاموظیفه» بهجای طبقههای مشخصکننده ویژگیها آمدهاند. اما هر ویژگی یک طبقه را معین میکند، طبقه همهچیزهایی که آن ویژگی را دارند، بنابراین این نوع گزارهها دارای یک گزاره منطقاً همارز بهصورت حملی هستند. دو گزاره اخیر متناظر با گزارههای I و E «بعضی گلها زیبایی هستند» و «هیچ کشتی جنگی چیز آماده انجاموظیفه نیست» هستند. این دو گزاره بهصورت گزارههای حملی هستند که در آنها بجای حد محمول، عبارت وصفی آمده است، برگردان آنها به گزارههای حملی استاندارد با جایگزینی محمول وصفی با عبارتی انجامگرفته که مشخصکننده طبقهای از همهچیزهایی است که آن صفت میتواند بهدرستی به آنها نسبت داده شود.
ج- گزارههایی که فعل اصلی آنها غیر از پیوند "بودن" در ساختهای استاندارد است.
مثالهایی از این نوع بسیار معمول هستند، مانند: «همه مردم درآمد دارند» و «بعضی مردم شراب یونانی مینوشند». روش معمول برای برگردان این گزارهها بهاینترتیب است که تمام گزاره بهجز حد موضوع و سور را بعنوان یک نامگذاری برای ویژگی تعریفکننده یک طبقه در نظر گرفته، و سپس آن واژهها را با عبارتی که مشخصکننده ویژگی تعریفکننده طبقه است جایگزین نمود و بعلاوه آن را با پیوند استاندارد به حد موضوع پیوند داده. بنابراین دو مثال ارائهشده وقتی بهصورت گزارههای حملی استاندارد برگردان شوند، عبارتاند از: «همه مردم درآمددار هستند» و «بعضی مردم شراب یونانی نوشنده هستند.»
د- گزارههایی که در آنها همه اجزای گزارههای حملی استاندارد حضور دارند اما بهصورت استاندارد مرتب نشدهاند.
دو مثال از این نوع عبارتاند از «اسبهای مسابقه همه اصیل هستند» و «همه آن چیزهایی خوب هستند که خوشعاقبتاند». در این موارد ابتدا مشخص کرده که حد موضوع کدام است و سپس پیکربندی واژهها را به قسمی مرتب کرده تا صورت استاندارد-ساخت حاصل شود. اینگونه برگردان معمولاً سرراست است. دو گزاره مثال بهصورت گزاره A «همه اسبهای مسابقه اصیل هستند» و «همهچیزهایی که خوشعاقبتاند خوب هستند» برگردان میشوند.
ه- گزارههای حملی که سور آنها واژههایی غیر از سورهای استاندارد "همه،"هیچ" و "بعضی" است.
گزارههایی که توسط واژه "هر" آغاز میشوند بهسادگی قابل برگردان هستند. گزاره «هر همکاری قدردانی خواهد شد» به «همه همکاریها چیزهای قدردانی شدنی هستند» برگردان خواهد شد. و به همین ترتیب نیز برای "هرکدام"، "هر چیزی" یا "هرچه میخواهد باشد" رفتار خواهد شد. برای عبارتهایی مثل "هرکه"، "هرکس"، "هرکسی"، "هر فردی"، "کسی"، "هر آنکه" یا "آنکه" وقتی مشخص باشد که طبقه مورداشاره محدود به انسانها است، مطابق با آنچه گفته شد رفتار خواهد شد، و مشکلی نیز نباید ایجاد گردد.
واژه "یک" (ازنظر دستور زبانی بعنوان حرف تعریف) نیز میتوانند بهصورت سور بعنوان "همه" یا "بعضی" که عمدتاً به زمینه متن بستگی دارد عمل نماید. بنابراین «یک خفاش یک پستاندار است» و «یک فیل حیوان پوستکلفت است» و همینطور «خفاش پستاندار است» و «فیل حیوان پوستکلفت است» بهطور قابلقبول به «همه خفاشها پستاندار هستند» و «همه فیلها حیوانات پوستکلفت هستند» برگردان میشوند. اما آشکار است که «یک خفاش پشت پنجره پرواز میکند» و «یک فیل فرار میکند» ارجاع به همه خفاشها یا فیلها ندارند. برگردان آنها «بعضی خفاشها موجوداتی هستند که پشت پنجره پرواز میکنند» و «بعضی فیلها موجوداتی هستند که فرار میکنند» است.
گزارههای ایجابی شروعشده با "هر"، به "همه P - S است" برگردان میشوند، گزارههای سلبی شروعشده با "نه هر" مثل «نه هر P S است» به «بعضی P - S نیست» برگردانده میشوند.
و- گزارههای ویژهساز. گزارههای حملی که در آنها واژه "فقط / تنها" بکار رفته.
این گزارهها موسوم به گزاره ویژهساز (/ گزاره حصری) هستند. زیرا آنها بهصورت کلی دلالت بر آن دارند که محمول بهطور انحصاری به موضوع نسبت داده شده. مثالهایی از این نوع عبارتاند از: «فقط شهروندان حق رأی دارند» یا «تنها شجاعان سزاوار انصاف هستند». مثال اول به گزاره حملی استاندارد-ساخت «همه حق رأیداران شهروند هستند» و گزاره دوم به گزاره حملی استاندارد-ساخت «همه سزاواران انصاف شجاع هستند» برگردانده خواهند شد. گزارههای شروعشده با "فقط" و "نه همه بلکه" معمولاً با کاربرد قاعده زیر به گزاره A برگردانده میشوند:
موضوع و محمول را جابجا کرده و "همه" را جایگزین "فقط" نموده.
بنابراین برگردان "فقط P - S است" و نیز "هیچچیز مگر P - S" گزاره "همه S - P است" خواهد بود، و همینطور برگردان "تنها P - S است"، "همه S - P است" است.
بعضی زمینهها هست که در آنها "فقط" و"تنها" دربردارنده معنی بیشتری هستند. در این مواقع "فقط P - S است" یا "تنها P - S است" میتوانند پیشنهادکننده "همه P - S است" یا "بعضی P - S است" باشند. اما همیشه این حالت نیست. البته، وقتی زمینه متن کمک به فهم چنین تصوری را مینماید باید آن را در نظر گرفت. اما، در نبود آگاهی بیشتر برگردان اول پیشنهادشده قابلقبول است.
ز- گزارههای حملی که بهکلی فاقد واژهای هستند که دلالت بر سور نماید.
دو مثال از این نوع عبارتاند از «سگ گوشتخوار است»" و «بچهها آمادهاند». وقتی سور وجود ندارد، فهم اینکه گزاره چه میخواهد بگوید ممکن است تردید برانگیز باشد. امکان دارد معنای آنها را فقط بتوان با توجه به زمینه متن تعیین کرد، و این بررسی معمولاً تردید را برطرف خواهد کرد. در مثال اول بهاحتمال بیشتر، منظور همه سگها هستند و برگردان آن «همه سگها گوشتخوار هستند» است. در مثال دوم روشن است که فقط بعضی بچهها موردنظر هستند و بنابراین برگردان آن «بعضی بچهها آماده هستند» خواهد بود.
ح- گزارههایی که شباهت به گزارههای حملی استاندارد-ساخت ندارند، اما میتوان آنها را به ساختهای استاندارد برگرداند.
بعضی مثالها عبارتاند از «نه همه بچهها دیو را باور دارند»، «فیل سفید وجود دارد»، «فیل صورتی وجود ندارد»، «هیچچیزی هم گرد و هم چهارگوش نیست» با تأمل میتوان پی برد که این گزارهها منطقاً همارز با برگردانشدههای زیر هستند. «بعضی بچهها باورمند دیو نیستند»، «بعضی فیلها اشیاء سفید هستند»، «هیچ فیلی شئ صورتی نیست»، «هیچ شئ گردی شئ چهارگوش نیست.»
ط- گزارههای استثناساز.
بعضی مثالها از این نوع عبارتاند از «همه بهجز کارمندان قابلپذیرش هستند»، «بهغیراز کارمندان قابلپذیرش هستند»، «کارمندان فقط قابلپذیرش نیستند» برگردان گزارههای جداساز (نیر گزارههای استثناساز) تااندازهای پیچیده است، زیرا گزارههایی از این نوع بجای یک ادعا دارای دو ادعا هستند (مانند گزارههای تکینه.) برگردان همارز منطقی «همه بهجز کارمندان قابلپذیرش هستند» فقط «همه غیرکارمندان قابلپذیرش هستند» نیست بلکه (درزمینهٔ عادی) همچنین عبارت است از «هیچ کارمندی قابلپذیرش نیست.» اگر کارمندان را با S و افراد قابلپذیرش را با P کوتاهنویسی کنیم، این دو گزاره میتوانند بهصورت «همه غیرP - S است» و «هیچ P - S نیست» نوشته شوند. روشن است که این دو مستقل هستند و بهاتفاق میگویند S و P طبقههای متمم هستند.
هرکدام از این گزارههای استثناساز گزاره مرکب هستند و بنابراین نمیتوانند به یک گزاره حملی استاندارد-ساخت برگردان شوند. بجای آن باید به دو گزاره که بهطور صریح به هم ربط دادهشدهاند برگردانده شوند. بنابراین سه گزاره مثال زده بهطور یکسان به "همه غیر کارمندان افراد نپذیرفتنی هستند" و "هیچ کارمندی فرد پذیرفتنی نیست" برگردان میشوند.
باید توجه داشت که بعضی استدلالها برای اعتبار وابسته به اطلاعات عددی یا شبه عددی هستند. این استدلالها در گزارههای تشکیلدهنده خود ممکن است کمیتها را مشخصتر از گزارههای حملی استاندارد بیان نمایند، برای مثال با اندازهگرهایی مانند "یک"، "دو"، "سه"، "خیلی"، "کمی"، "بیشتر" و مانند اینها. وقتی اینچنین اطلاعات کمّی برای اعتبار برهانی که در آن به میان آورده شدهاند اساسی است، استدلال غیر قیاسی است، و نیاز به تحلیل پیچیدهتر ازآنچه توسط نظریه ساده استدلالهای قیاسی ارائه میگردد وجود دارد. بااینحال بازهم هنوز سورهای شبه-عددی در استدلالها میتواند وجود داشته باشد به قسمی که تحلیل قیاسی را میسر سازد. ازجمله میتوان از "تقریباً"، "نه کاملاً همه"، "همه بهجز معدودی" و "فقط تعدادی" نام برد. گزارههایی که در آنها اینگونه اندازهنماها بکار رفتهاند را میتوان مانند گزارههای استثناساز تحلیل کرد. در گزارههای مرکب زیر اندازهنماهای شبه-عددی بکار رفته است؛
«تقریباً همه دانشجویان در جشن حضور داشتند»، «نه همه دانشجویان در جشن حضور داشتند»، «فقط بعضی از دانشجویان در جشن حضور داشتند» و «همه بهجز تعداد اندکی از دانشجویان در جشن حضور داشتند».
هرکدام از آنها تأیید میکند که بعضی از دانشجویان در جشن حضور داشتند و درعینحال انکار میکند که همه دانشجویان در جشن حضور داشتند. آگاهی شبه عددی که آنها در بر دارند ازنقطهنظر استدلال قیاسی بیارتباط است و همه بدون تفاوت بهصورت (بعضی دانشجویان افرادی هستند که در جشن حضور داشتند، و بعضی از دانشجویان افرادی هستند که در جشن حضور نداشتند) برگردان میشوند.
از آنجائیکه گزارههای استثناساز گزاره حملی نیستند و درواقع گزاره عطفی هستند، بنابراین با توجه به نگاه ما به اصطلاح استدلال قیاسی یک استدلالِ دارای گزاره استثناساز یک استدلال قیاسی نیست. بااینوجود، آنها مستعد برای تحلیل و برآورد قیاسی هستند. اینکه چگونه یک استدلال دارای گزاره استثناساز باید مورد آزمون قرار گیرد، بستگی به موقعیت گزاره استثناساز در استدلال دارد. اگر مقدمه است، آنگاه ممکن است استدلال نیازمند به آزمون جداگانه باشد. برای مثال استدلال زیر را مشاهده نمایید:
هرکس که بازی را مشاهده کرده در جشن حضورداشته.
نه همه دانشجویان در جشن حضور داشتند.
ـــــــــــــــــــ
بنابراین بعضی دانشجویان بازی را مشاهده نکردهاند.
مقدمه اول و نتیجه، گزارههای حملی هستند، که بهآسانی بهصورت استاندارد قابل برگردان هستند. اما مقدمه دوم یک گزاره استثناساز است؛ یعنی نه یک گزاره ساده، بلکه یک گزاره مرکب است. برای فهمیدن اینکه آیا مقدمات مستلزم نتیجه هستند، ابتدا باید قیاسی که عبارت از مقدمه اول و نیمه اول مقدمه دوم و نتیجه است را برآورد کرد، بنابراین خواهیم داشت:
همه افراد شاهد بازی حاضر در جشن بودند.
بعضی دانشجویان افراد حاضر در جشن بودند.
ـــــــــــــــــــ
بنابراین بعضی دانشجویان افراد بیننده بازی هستند.
صورت این استدلال یک قیاس حملی استاندارد-ساخت AIO-۲ است که مبتلا به مغالطه حد وسط توزیعنشده است، یعنی قاعده ۲ را رعایت نکرده است. اما هنوز ثابت نشده است که استدلال اصلی نامعتبر است، زیرا قیاسی که هماکنون بررسی شد شامل فقط بخشی از مقدمات استدلال اصلی است. باید قیاس حملی متشکل از مقدمه اول و نتیجه و نیمه دوم مقدمه دوم را مورد آزمون قرار داد. در این حالت و در شکل استاندارد ما استدلال کاملاً متفاوتی را خواهیم داشت.
همه افرادی که بازی را دیدهاند، افرادی هستند که در جشن حضور داشتند.
بعضی دانشجویان افرادی نیستند که در جشن حضور داشتند.
ـــــــــــــــــــ
بنابراین بعضی دانشجویان افراد نیستند که بازی را دیدهاند.
این، قیاس حملی استاندارد-ساخت AOO-۲ (باراکو) است، و بهآسانی میتوان نشان داد که معتبر است. بنابراین، استدلال اصلی معتبر است، زیرا نتیجه یکسان است و مقدمات استدلال اصلی شامل مقدمات این قیاس استاندارد-ساخت هستند. بنابراین برای آزمون یک استدلال، که یکی از مقدمات آن گزاره استثناساز است، ممکن است نیاز به آزمون دو قیاس استاندارد-ساخت جداگانه باشد.
اگر مقدمات یک استدلال هردو گزارههای حملی باشند، و نتیجه استثناساز باشد، روشن است که استدلال نامعتبر است، زیرا دو گزاره حملی فقط میتوانند یکنیمه یا نیمه دیگر نتیجه مرکب را دربر داشته باشند، آنها نمیتوانند هردو گزاره را باهم نتیجه دهند، برای اثبات استدلال ممکن است نیاز باشد تا همه قیاسهای قابل ساختن از استدلال اصلی مورد آزمون قرار گیرند. اکنون دیگر نیاز به ادامه بحث نیست و اینجا کفایت بحث را برای توانمندی دانشجویان در ازعهده برآمدن اینچنین شرایط را اعلام میکنیم.
روشهای آزمون اعتبار استدلال که تاکنون گسترش داده شد— نمودارهای ون و قواعد قیاسی— فقط در مورد قیاسهای حملی استاندارد-ساخت قابل کارگیری مستقیم هستند. بنابراین بسیار مهم است تا روانشدن و سهولت را در برگردان انواع بسیار گزارههای غیراستاندارد به گزاره استاندارد بدست آورد.
تمرین
گزارههای زیر را به گزارههای حملی استاندارد – ساخت برگردان نمایید :
۱- رزها خوشبویند
حل:
برگردان استاندارد- ساخت : همه رزها چیزهای خوشبو هستند.
۲- ارکیدهها خوشبو نیستند.
۳- زندگی درازتر افسوس جوانی ازدسترفته.
۴- نه هر کس که ارزش ملاقات دارد ارزش دوستی هم دارد.
۵- اگر این، یک جونکو است، بهترین چیزی است که میتوان با پول خرید.
حل:
همه جونکوها بهترین چیزهایی هستند که میتوان با پول خرید.
۶- چیزی که نوشیدنی گازدار واقعی نیست کوکاکولا هم نیست.
۷- هیچچیزی هیجان بخش و هم بیخطر نیست.
۸- تاکنون فقط افراد شجاع توانستهاند به مدال افتخار نائل آیند.
۹- مشاوران خوب عموماً مورد قدردانی درخور قرار نمیگیرند.
۱۰- کسانی که صورتشان به سمت خورشید است سایه خود را نمیبینند.
حل:
هیچ فردی که صورتش به سمت خورشید است سایه خود را نمیبیند
۱۱- شنیدن آوای او خود یک الهام است.
۱۲- کسی که شمشیر برگزید با شمشیر هلاک شد.
۱۳- فقط اعضا میتوانند از درب جلوئی استفاده کنند.
۱۴- هیچکس دوستدار سارا نیست.
۱۵- گروه آبیها هیچ نامزد گروه نارنجیها را پشتیبانی نمیکنند.
حل:
هیچ نامزد نارنجیها کسی نیست که توسط آبیها پشتیبانی شود.
(یا هیچ آبی پشتیبان نارنجیها نیست.)
۱۶- هر سبکی خوب است مگر خسته کنندهها.
۱۷- آنها کسانی را فقط بایستند و منتظر بمانند را هم پذیرایی میکنند.
۱۸- شادی در اوست که آگاه به محدودیتهای خویش است.
۱۹- یک زیبایی یک شادی همیشگی است.
۲۰- کسی آراسته نماز برپای میدارد که بیپیرایه عاشق است.
حل:
همه عاشقان بیپیرایه نمازگزار آراستهاند.
۲۱- هرچه بدرخشد طلا نیست.
۲۲- هیچکس به اندوه بزرگ نمیاندیشد مگر بزرگ.
۲۳- او که ترس را به استهزا میگیرد حتی زخمی هم هرگز ندیده.
۲۴- هرچه بکاری همان بدروی .
۲۵- سخنی نرم دشمنی را فراری میدهد.
حل:
همه سخنان نرم چیزهایی هستند که دشمنی را فراری میدهند.
