مسئله و استدلال
تحلیل استدلال
درآمد به منطق فصل ۲ قسمت ۳
در قسمت پیشین و پیشتر از آن پیگیر آشکار کردن ساختار استدلال در زبان بودیم و استدلالهایی از بزرگان خرد را دیدیم. هرچه هست، این برهانآوریها برآمده از پرسشی آراسته و پیراسته (مسئله) بود. ما اغلب وقتی اغتشاش در وضعی را حس نماییم كه پیشتر پرسشی روشن و جوابی درخور داشته است، به حضور مسئلهای در زندگی پیمیبریم. حل مسئله روندی است ذهنی، که مستلزم تحلیل موضوعی از گونهای است. اندیشیدن بازتابانه درهر قلمرو، کنشورزیِ حل مسئله است. در این قسمت با آوردن مثالهایی از مسایلِ ازپیشساخته، که اغلب پیچیدگیهایی از مسائل واقعی را درخود دارند، به مسئله و استدلال برای آن (حل مسئله) میپردازیم. و ازجمله با آنچه را که «تحلیل به شیوهِ پسگستر» (Retrograde Analysis) مینامند، آشنا میشویم.
۳.۲ مسئله و استدلال
■ مساله چیست؟
استدلال روندی است كه از مقدمات دانسته (یا مفروضات، یعنی مقدماتی که فعلاً درست فرض شده) آغاز و بهسوی نتیجه یا نتیجههای برآمده از آنها پیش میرود. ما خود درگذر ایام استدلالهای خود را میسازیم تا تصمیم بگیریم چگونه در برخورد با حوادث رفتار نماییم، به داوری در كردار دیگران بنشینیم، دفاع از منش یا آمال سیاسی خود نماییم، و همه اینها و نیز بسیاری دیگر. مهارت در ساختن و بكارگرفتن خوب و بجای این دلیلآوریها كه سرانجام به كردار ما منجر خواهندشد، ارزش مهم و بس والا دارند.
مسائل از پیش تدوینیافته شستهرفتهتر از مسائل واقعی (برخاسته از زندگی) و معمولاً خیلی سادهتر از آنها هستند. پرداختن به آنها میتواند نیازمند به اندیشهورزی باشد و افزون بر آن چالشبرانگیز هم باشد؛ حل آنها در بیشتر مواقع مستلزم گسترش نوعی استدلال است كه با نمونههای بکار بسته توسط كارآگاهان، خبرنگاران، و اعضای هیئتهای منصفه چندان متفاوت نیست. بهعبارتدیگر، برای رسیدن به جواب یا جوابهای مسئله نیاز به تشكیل زنجیرههایی از استخراج نتایج (استدلال) است كه این نتایج به سهم خود باید بهعنوان مقدمات (نتیجههای فرعی / میاننتیجهها) برای استنتاجهای بعدی بکار گرفته شوند. در حل این مسائل ممکن است گاهی به استفاده از فراست و درواقع سماجت بیشتر نیاز باشد. پیدا کردن مسیر منجر به حل در آنها ممکن است مستلزم جمعبندیِ دوباره اطلاعات دادهشده و حتی نتایج بهدستآمده در یك مرحله از مسیرِ حل باشد. حل و تمرین مسائل از پیش تدوینیافته میتواند بسیار مشكل و گاهی حتی ناامیدكننده باشد — اما حل آنها مانند هر كامیابی برآمده از استدلال بسیار خرسندكننده است. معماها و بازیهای منطقی افزون براینکه میتوانند بهعنوان مدل بکارروند تا استدلال را با آنها تمرین كرد — سرگرمی خوبی نیز هستند. "شادی حاصل از برخورد با شك" به گفته جان دیویی فیلسوف آمریکایی "یك نشانه ذهنِ آموخته است." [و نیز از ارسطو: "سرگرمشدن با اندیشهای که نپذیرفتهای، نشانه یک ذهنِ آموخته است."]
■ مسئله و چرخه حل مسئله
اندیشیدن بازتابانه — خواه در جامعه شناسی، پزشکی، حقوق، فیزیک یا در هر قلمروی — کنشورزی حل مسئله است. بهعبارتدیگر، حل مسئله روندی است ذهنی که مستلزم تحلیل و آشکارسازی موضوعی از گونهای است. چرخه حل مسئله رهیافتی برای حل مسئله است که در آن مراحل معینی بهطور مکرر (موسوم به چرخه) اجرا میگردد به قسمی که هر چرخه از چرخه قبل آشکاری بیشتر به مسئله بتاباند تا سرانجام به حل مسئله، حلناپذیری مسئله یا بیحاصل شدن چرخهها (باز باقیماندن مسئله) بیانجامد.
در شکل زیر (شکل ۱) گونهای از چرخه حل مسئله (توصیه شده توسط جرج پولیا اینجا و اینجا) را میتوان دید.
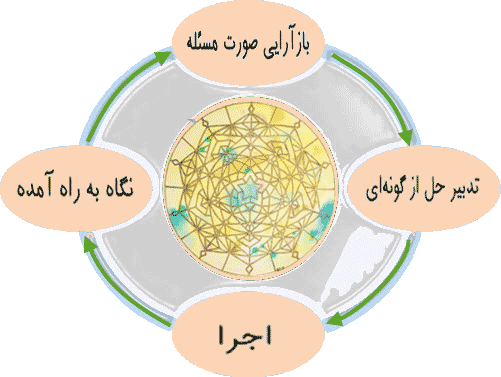
■ حل مسئله
در نوع رایجی از این معماها (مسائل از پیش تدوینیافته) تعدادی سرنخ ارائه و خواسته میشود تا بهتشخیص نام، نقش، یا واقعیتهای دیگر درباره یك یا چند ویژگی معین پیبرده شود. دراینجا مثال سادهای آمده است:
خدمه پرواز یك هواپیما عبارتاند از آریـن، بـاربـد و كیـوان. مشاغل آنها در این پـرواز، نه الزاماً به ترتیبی كه نامهایشان آمد: خلبان، كمکخلبان و مهندس پرواز است. هر شغل نیز فقط توسط یك فرد اداره میشود.
كمكخلبان كه تنها فرزند خانواده خود است كمترین حقوق را میگیرد.
كیوان كه با خواهر باربد ازدواجکرده بیشتر از خلبان حقوق میگیرد.
شغل هر یك را تعیین نمایید.
در حل اینگونه مسائل ابتدا باید به دنبال میدانی بود كه در آن اطلاعات كافی برای استخراج نتایجی بیش ازآنچه در مقدمات هست، موجود باشد. در این مسئله بیشتر از همه در مورد كیوان اطلاعات داریم: او خلبان نیست، زیرا ماهانه او بیشتر از خلبان است؛ و كمكخلبان هم نیست چون كمكخلبان كمترین ماهانه را دارد. از روش حذف میتوان نتیجه گرفت: كیوان باید مهندس پرواز باشد. از این نتیجه فرعی اخذشده میتوان به شغل باربد پیبرد. از آنجا که باربد یك خواهر دارد و كمكخلبان تكفرزند است پس باربد كمكخلبان نیست؛ او مهندس پرواز هم نیست چون این شغل كیوان است. بنابراین باربد باید خلبان باشد. اكنون تنها آرین باقیمانده و بنابراین او باید كمكخلبان باشد.
وقتی مسئلههایی ازایندست پیچیدهتر میشوند، یک روش مفید ساختن یک نمای گرافیکی موسوم به ماتریس از گزینههای ممکن و پرکردن آن با اطلاعات جدید فراهمشده است. سودمندی چنین ماتریسی در حل مسئلهای که درپی آمده خواهیم دید.
آرین، كیوان، رحمان، وحید چهار هنرمند خلاق هستند. یكی از آنها بالرین، دیگری نگارگر، یکی هم خواننده و دیگری نویسنده است و البته نه الزاماً به ترتیبی كه نامهایشان آمد.
(۱) آرین و رحمان در شبی كه خواننده اولین برنامه خود را اجرا کرده بود در میان تماشاگران بودند.
(۲) تصاویر كیوان و نویسنده را همیشه نگارگر كشیده است.
(۳) نویسنده، كه زندگینامه نوشتهشده توسط او از وحید در میان كتب پرفروش بوده، قصد دارد زندگینامه آرین را نیز بنویسد.
(۴) آرین تاکنون هیچچیز از رحمان نمیداند.
زمینه كار هنری هر یك را تعیین نمایید.
حفظ کردن واقعیات آمده در صورتمسئله و میاننتیجههای قابل دریافت از آنها كاری طاقت فرسا است. یادداشت نتایج به شکل نوشتن معمولی میتواند تاحدی مفید باشد، اما میتواند به یك كلاف سردرگم هم منجر شود. نیاز به روشی است تا بهوسیله آن اطلاعات صورتمسئله و نتایج حاصله میانی را مرتب و آماده نگاهداشت، روشی كه، چیزهایی را كه میدانیم و یا طی حل مسئله به آنها دستیافتهایم را همزمان با گسترش زنجیره استنتاجها و افزایش نتایج، بهصورت منظم نگهداریکند و بعلاوه بهآسانی در دسترس قراردهد. ماتریس ساختاری جدولی است كه در آن، خانههایی برای نگهداری و نمایاندن همه رویدادهای ممكنه و میان نتیجهها، آماده شده است.
ماتریس دراین مسئله باید آرایهای را برای چهار نفر (در چهار سطر) و بعلاوه برای چهار زمینه هنری (در چهارستون) كه هریك ازاین افراد دارند دراختیار بگذارد. این ساختمان جدولی باید بهشکل آنچه در زیر آمده باشد:
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | ||||
| کیوان | ||||
| رحمان | ||||
| وحید |
در مسیر حل وقتی پیبردیم، فردی كه نام وی در ستون سمت راست آمده نمیتواند صاحب آن زمینه هنری باشد كه عنوان آن در بالای هر ستون مشخصشده، آنگاه در خانهای از خانههای سمت چپ (هم سطر با نام وی)، و واقع در ستونی با این عنوان هنری، حرف "ن" را (به نمایندگی “نادرست“)، میگذاریم. در آغاز حل این مسئله و بدون هیچ واسطهای میتوان نتیجه گرفت كه (مقدمه ۱) آرین و رحمان، هیچکدام، خواننده نیستند. بنابراین در خانههای سمت چپ نام آنها و واقع در ستون سوم (خواننده) حرف ن را قرار میدهیم. بهروش مشابه میتوان از مقدمه ۲ نتیجهگرفت كه كیوان نه نگارگر و نه نویسنده است، بنابراین حرف ن را در سمت چپ نام او در خانههای واقع در ستون دوم (نگارگر) و ستون چهارم (نویسنده) قرار میگذاریم. از مقدمه ۳ پیمیبریم نویسنده نه آرین است و نه وحید، بنابراین حرف ن را در سمت چپ نام آنها در ستون چهارم قرارمیدهیم. اقلامی را كه تاكنون ثبتکردیم همه از اطلاعات اصلی و دادهشده بهدستآمده، اكنون ماتریس باید به شکل زیر درآمده باشد:
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | ن | ن | ||
| کیوان | ن | ن | ||
| رحمان | ن | |||
| وحید | ن |
از طلاعاتی كه اكنون در اختیارداریم (در آرایههای ماتریس نمایان است) و کاربرد قاعده حذف میتوان نتیجه گرفت رحمان باید نویسنده باشد، بنابراین حرف د ("درست") را در خانه سمت چپ نام او و در ستون چهارم (نویسنده) میگذاریم
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | ن | ن | ||
| کیوان | ن | ن | ||
| رحمان | ن | د | ||
| وحید | ن |
و یک ن در هریک از خانههای باقیمانده سمت چپ این نام میگذاریم:
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | ن | ن | ||
| کیوان | ن | ن | ||
| رحمان | ن | ن | ن | د |
| وحید | ن |
این آرایه (ستون نگارگر) آشکار میکند نگارگر باید آرین یا وحید باشد. آرین را میتوان با این روش حذف کرد كه: میدانیم تصویر رحمان توسط نگارگر كشیده شده است (مقدمه ۲)، و آرین هیچچیز درباره رحمان نمیداند (مقدمه ۴) — بنابراین آرین نمیتواند نگارگر باشد. پس میتوان حرف ن را سمت چپ نام آرین در ستون دوم (نگارگر) گذاشت. اکنون جدول بهصورت زیر درآمده است:
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | ن | ن | ن | |
| کیوان | ن | ن | ||
| رحمان | ن | ن | ن | د |
| وحید | ن |
در مرحه بعدی نتیجه میگیریم كه آرین باید بالرین باشد، لذا حرف د را سمت چت نام او در ستون اول (بالرین) گذاشته.
| بالرین | نگارگر | خواننده | نویسنده | |
| آرین | د | ن | ن | ن |
| کیوان | ن | ن | ||
| رحمان | ن | ن | ن | د |
| وحید | ن |
حالا میتوان یك ن در همین ستون برای كیوان و وحید گذاشت.
| بالرین | گارگر | خواننده | نویسنده | |
| آرین | د | ن | ن | ن |
| کیوان | ن | ن | ن | |
| رحمان | ن | ن | ن | د |
| وحید | ن | ن |
تنها فقره باقیمانده و ممكن برای كیوان خواننده است و لذا حرف د را در خانه مربوط و ن را در ستون خواننده و سمت چپ نام وحید گذاشته.
| بالرین | نگرگر | خواننده | نویسنده | |
| آرین | د | ن | ن | ن |
| کیوان | ن | ن | د | ن |
| رحمان | ن | ن | ن | د |
| وحید | ن | ن | ن |
دوباره توسط حذف به این نتیجه میرسیم كه وحید باید نگارگر باشد و لذا یك د در آخرین خانه خالی باقیمانده گذاشته. اكنون مدل نمایشی ما بهصورت زیر درآمده است:
| بالرین | نگاگر | خواننده | نویسنده | |
| آرین | د | ن | ن | ن |
| کیوان | ن | ن | د | ن |
| رحمان | ن | ن | ن | د |
| وحید | ن | د | ن | ن |
ماتریس ما اکنون دیگر پرشده است و جواب کامل آشکار است: آرین بالرین؛ كیوان خوانند؛ رحمان نویسنده؛ و وحید نگارگر است.
بعضی مسائل بغرنج از این نوع که نیازمند به حل در چندین بعد هستند بسیار چالش آور میشوند و مشكل بتوان آنها را بدون استفاده از ماتریس حل کرد.
شما با شش كره روبرو هستید: دو قرمز، دو سبز، و دو آبی. همچنین میدانید در هر زوج همرنگ كرهها یكی از دیگری سنگینتر است. افزون برآن میدانید كه سه كره سنگینتر هموزن هستند، و همینطور سه كره سبکتر نیز هموزن هستند. این شش كره كه آنها را ب R1 ,R2 ,G1 ,G2 ,B1 ,B2 نشان میدهیم به طریق دیگری قابل تمیز نیستند. علاوه بر كرهها یك ترازو نیز موجود هست.
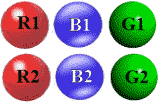
اکنون پرسش مسئله:
فقط با دو اندازهگیری توسط ترازو، چگونه میتوان كره سنگینتر و كره سبکتر را در هریك از این سه گروه مشخص كرد؟
حل: ابتدا توزین R2+B1 R1+G1
R1+G1
اگر آنها هموزن باشند:

در این حالت، از مقدمات مسئله میدانیم از زوج R1 و R2، یكی سنگینتر و دیگری سبکتر است. با داشتن دو كره قرمز در كفههای مجزا، باید از دو كره دیگر یكی سنگینتری و دیگری سبکتری باشد، زیرا دو سنگین در یك كفه ترازو آن را پایین میآورند و دو سبك در یك كفه آن را بالا میبرند. بنابراین تاكنون دانسته شد كه:
G1سنگینتری و B1 سبكتری است یا G1سبكتری و B1 سنگینتری است.
نتیجه بالا راهگشا برای توزین بعدی است. پس اگر در توزین اول دو طرف برابر بودند:
 B1
B1 اگر(در این توزین) G1 پایین برود:
B1سبكتری است (و B2 سنگینتری است)؛ و
R1سبكتری است (و R2 سنگینتری است).
اما چنانچه در توزین اول R2+B1 R1+G1 دو کفه ترازو میزان نباشند چه رخ خواهد داد؟ فرضکنید كفه R1+G1 پایین برود. (اگر R1+G1 بالا برود، حل وارون خواهد بود):
R1+G1 دو کفه ترازو میزان نباشند چه رخ خواهد داد؟ فرضکنید كفه R1+G1 پایین برود. (اگر R1+G1 بالا برود، حل وارون خواهد بود):
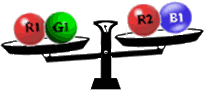
میدانیم در این حالت R1 (كره قرمز در كفهای كه پایینرود) باید سنگینتری باشد؛ زیرا اگر R1 سبكتری بود R2 سنگینتری میشد. و اگر R2 سنگینتری بود، كفه R1+G1 نمیتوانست پایین برود.
ازآنجاییکه R1 سنگینتری است، یكی از حالات زیر باید رخ دهد.
| (آ) | : | G1 سبكتری است و B1 سبكتری است؛ |
| (ب) | : | G1 سنگینتری است و B1 سنگینتری است؛ |
| (ج) | : | G1 سنگینتری است و B1 سبكتری است. |
ملاحظات بالا راهگشا بهاین است که اگر در اولین توزین R1+G1 پائینرود توزین دوم بهقرار : R1+R2  G1+B1 خواهد بود.
G1+B1 خواهد بود.
اكنون میدانیم كه R1 سنگینتری است. در توزین دوم، كفه R1+R2 (سنگینتری+سبکتری) باید پایین یا بالا رود یا دو کفه میزان باشند. در هر سه حالت همه كرهها را میتوان بهروش زیر مشخص نمود:
| ۱- | اگر كفه R1+R2 پایین باشد آنگاه G1 و B1 باید هردو سبكتری باشند (زیرا یك سنگین و یك سبك سنگینتر از دو سبك است). در این حالت تركیب (آ) كه در بالا آمده بهصورت زیر درخواهد آمد: G1سبكتری و B1سبكتری — و باقی مسئله نیز حلشده است. |
| ۲- | اگر كفه R1+R2 بالا باشد G1 و B1 باید هردو سنگینتری باشند (زیرا یك سنگین+یك سبك باید از دو سنگین سبكتر باشند). در این حالت تركیب (ب) كه در بالا آمده بهصورت زیر درخواهد آمد: G1سنگینتری و B1سنگینتری — و باقی مسئله نیز حلشده است. |
| ۳- | اگر دو كفه میزان شوند G1 و B1 باید بهصورت یک سنگین + یک سبک باشد. در این حالت تركیب (ج) كه در بالا آمده بهصورت زیر درخواهد آمد: G1 سنگینتری و B1 سبكتری — و باقی مسئله نیز حلشده است. |
در مسائل واقعی، بیشتر اوقات باید برای علت یك وضعیت رخداده دلیلیابی نمود، یعنی از چیزی که هست بهسوی آن چیز كه بود رفت. دانشمندان — بهویژه باستانشناسان، زمینشناسان، فیزیكدانان، و پزشكان — اغلب با مسائلی مواجه میشوند كه سرچشمه آنها چندان روشن نیست و بهعبارتدیگر پرسشبرانگیز هستند.
■ تحلیل پسگستر
آن استدلال، كه درپی آن است تا توضیحدهد، چگونه چیزها ازآنچه قبلاً بودند میبایست گسترش مییافتند تا چنین باشند که هستند، به تحلیل پسگستر (Retrograde analysis) موسوم است. برای مثال، در مقابل تعجب ستارهشناسان، در عبور ستاره دنبالهدار هایکوتاک (Hyakutake) از کنار زمین در سال ۱۹۹۶م مشاهده شد این ستاره ۱۰۰ برابر بیشتر پرتو ایكس ازآنچه حداكثر برای یك ستاره دنبالهدار پیشبینی میشد، پراكندهاست. یكی از كارشناسان ستارههای دنبالهدار در انستیتوی پلانك آلمان گفتهبود كه: "ما مجبوریم تا توضیح این دادهها صبر کنیم— اما این از آن نوع مسائلی است كه خود میخواهید با آن روبرو شوید."
درواقع چنین نیز است که خود میخواهیم با آنها مواجه شویم، و به همین دلیل مسائلی برای تحلیل به شیوه پسگستر تدبیر میشوند. در دنیای واقع، مسائل منطقی از درون یک چهارچوبکاری نظری که از دانستههای علمی یا تاریخی فراهمشدهاند برمیخیزد؛ اما، در مسائل از پیش تدوینیافته آن چهارچوبکاری نظری میباید توسط خود مسئله آماده شده باشد. دراین مسائل قواعدی باید بهمیان آوردهشوند تا توسط آنها تحلیل میسر گردد. صفحه شطرنج یک عرصه مشهور برای ارائه مسائل "تحلیل پسگستر" هست؛ قواعد شطرنج زمینه نظری موردنیاز را فراهم میسازند. گرچه صرف بازی شطرنج مهارتی را نمیطلبد، خوانندگانی كه با قواعد این بازی آشنا نیستند میتوانند ازآنچه در پی آمده، درگذرند.
مسائل پسگستر در شطرنج بهطور کلی دارای قالبی به این صورت هستند كه: ترتیبی از مهرههای چیده شده در صفحه شطرنج ارائه میشود؛ این ترتیب چینش، ناشیشده از بازیای هست كه در آن همه قواعد رعایت شدهاند. پرسش ایناست: چه حركات یا دنباله حركاتی تاکنون انجامیافته تا صحنه بدینگونه که هست درآمده؟ یك مثال ازاین نوع درپی آمده. نمودار صفحه شطرنج در مرحلهای از بازی نشان دادهشده است و در تمام حركات قبلی قواعد بازی شطرنج بهطور كامل رعایت گردیده است.

برای تحلیل، سطرها از پایین به بالا از شماره 1 تا 8 و ستونها از چپ به راست از حرف a تا h نشاندار شدهاند. بهاینترتیب هر خانه صفحه شطرنج بهطور منحصربهفرد بهصورت تركیب حرف-عدد متمایز میگردد: شاه سیاه در a8 است، پیاده سفید در h2، و بقیه نیز همانطور که در شکل دیدهمیشود هستند. مسئله بهاین صورت مطرح است: آخرین حركت را سیاه انجامداده است. این حركت چهبوده؟ افزون برآن، حركت سفید بلافاصله قبل ازآنچه چهبوده؟ آیا میتوانید قبلاز خواندن پاراگراف بعدی حل و استدلال آن را بیان نمایید؟
حـل:
شاه سیاه آخرین حركت را انجامداده. ازآنجاکه ممكن نیست دو شاه در خانههای مجاور باشند، مبدأ حركت نمیتواند خانه b7 یا خانه b8 باشد، بنابراین میتوان مطمئن بود که از خانه a7 حركت کرده است، جائی كه در حالت كیش بود.
جواب اول بهسادگی مهیاگردید. اما چه حركتی قبلاً توسط بازیكنِ سفید، شاه سیاه را در حالت كیش قرارداده؟ این حركت نمیتواند توسط وزیر سفید در g1 انجامشده باشد، زیرا راهی وجودنداشته كه وزیر سفید بهاین خانه، g1، حرکت کند، بدونآنكه شاه سیاه را در حالت اجبار به حركت توسط ایجاد كیش قراردهد! بنابراین كیش باید توسط حركتی توسط یكیدیگر از مهرههای سفید انجامشده باشد. یعنی این حركت باید باعثشود تا مانع برای وزیر سفید در حمله به شاه سیاه از بینبرود. چه مهره سفیدی میتواند در یك ردیف اریب از خانههای سیاه باشد و به خانهای سفید در گوشه حرکتکند؟ فقط اسبی كه در خانه b6 قرار داشته. بنابراین میتوان اطمینان داشت که قبل از آخرین حركت سیاه (حركت شاه سیاه از a7 به a8) آخرین حركت سفید انتقال اسب خود از b6 به a8 بوده است.
البته آشكار است، بعضی مسائل نیازمند به استدلال كه درگذر زمان ما را دربرابر خود میخوانند بندرت وصف آنها ( صورتمسئله) وضوح و شستهرفتگی معماهای مطرحشده در این بخش را دارند. بسیاری از مسائل واقعی بهدقت توصیف نمیشوند، و بد شرحی آنها میتواند منجر به كجراهه و نرسیدن به جواب گردد، در این حالت نیازاست تا بخش یا بخشهایی از توصیف مسئله حذف یا جایگزین گردد. اما، برای حل معماهای منطقی آنگونه كه در این بخش مشاهده شد، نمیتوان به این روش عمل نمود.
برای بعضی از مسائل واقعی حتی وقتی وصفی دقیقی از آنها ارائهشده، ممكن است هنوز این توصیف کافی نباشد و برای حل نیاز به دادههای ضروری دیگری باشد كه در دسترس نیستند. ممكن است حل مسئله به كشفیات علمی بیشتری وابستهباشد، یا به وسایل و اختراعاتی كه از قبل نیاز به آنها تصور نمیشد، یا جستجو در قلمروهایی كه هنوز كاوشی در آنها روی نداده و یا كشف نشدهاند. اما در بیان معماهای منطقی، مثلاً در شرح یك جنایت رازآلود، همه اطلاعات لازم برای حل باید ارائه شوند، درغیر اینصورت این احساس در ما انگیخته خواهد شد كه رازنویس، یا سازنده معما با ما منصف نبوده است.
سرانجام اینكه، در معماهای منطقی پرسش مسئله صریح و روشن است (برای مثال، كدامیك از چهار نفر خواننده است؟ آخرین حركت مهره سیاه و سفید چه بوده است؟) و چنانچه جواب پیدا شود قطعی خواهد بود. اما در بسیاری از مسائل برخاسته از دنیای واقع وضع بدین گونه نیست. ما اغلب وقتی به حضور مسئلهای واقعی در زندگی پیمیبریم (شاید به ناگهان هم باشد) كه، حداقل در آغاز ناسازگاری یا رویداد نامتعارفی حاصل شده است - یا وقتی حضور اغتشاش در وضعیتی را حس نماییم كه همیشه به همراه خود پرسشی سرراست و جوابی درخور نیز داشته.
باوجود همه این تفاوتها، مسائلی كه برای حل به شیوه برهان سامانمند طراحی میشوند بهقدر كافی شباهت با مسائل واقعی دارند تا بهكارگیری آنها در مطالعه منطق موجه باشد.
تمرین
برای حل مسائل زیر نیاز به استدلال هست. اثبات درستی یک جواب نیازمند به استدلالی (که اغلب شامل استدلاهای فرعی نیز هست) است که مقدمات آن در صورتمسئله آمدهاند- و نتیجه آن همان جوابی است که باید یافتهشود. اگر جواب صحیحباشد یک استدلال معتبر میتواند آن را اثباتکند. در حل این مسائل از خواننده بهطورجدی خواسته و پافشاری میشود که خود را صرفاً درگیر پیداکردن جواب ننماید، بلکه همچنین به پیكربندی استدلالهایی بپردازد که ثابت میکنند آن جوابها صحیحاند.
| ۱. | در یک جامعه ویژه و خیالی، سیاستمداران هرگز راست نمیگویند، غیر سیاسیون همیشه راست میگویند. یک غریبه سه نفر از اهالی این جامعه را ملاقات کرده و از اولی میپرسد، آیا شما یک سیاستمدار هستید؟ اولین نفر به پرسش جواب میدهد. فرد دوم بلافاصله میگوید، نفر اول انکار میکند که سیاستمدار است. نفر سوم میگوید که فرد اول سیاستمدار است. چندنفر ازاین سه نفر محلی سیاستمدارند. حل: برای دیدن حل کلیک کنید :[←] | ||||||||||
| ۲. | سه زندانی در یک زندان زندانی هستند. یکی از آنها بینایی کامل دارد. نفر دوم فقط از یك چشم بینا است و نفر سوم کاملاً نابینا است. زندانبان روزی به زندانیان گفت که از جعبهای شامل سه کلاه سفید و دو کلاه قرمز، او سه کلاه انتخاب خواهد کرد و آنها را بر سر زندانیان خواهد گذاشت. هیچکسی نمیداند چه رنگ کلاهی بر سر اوست. زندانبان به زندانی که بینایی کامل داشت گفت او اگر بتواند بگوید چه رنگ کلاهی بر سر دارد آزاد خواهد شد. برای آنکه زندانی با حدس و گمان جواب را نگوید، زندانبان زندانی را در صورت جواب غلط تهدید به مرگ نمود. زندانی اول نتوانست بگوید که کلاه وی چه رنگی است. به زندانی دوم نیز که از یک چشم نابینا بود چنین پیشنهادی شد. زندانی دوم نیز نتوانست بگوید چه کلاهی را پوشیده است. زندانبان نخواست زندانی سوم را که نابینا بود بیازارد و چنین پیشنهادی را نیز به او ارائه کند، اما موافقت کرد هرگاه خود خواست این پیشنهاد را به او هم کند. زندانی نابینا گفت: من نیازی به بینایی خود ندارم؛ | ||||||||||
| ۳. | خدمه یك قطار عبارتاند از راننده، مکانیک و مهندس. در قطار سه مسافر نیز بنامهای جونز، رابینسون و اسمیت وجود دارند. اطلاعات زیر را از این افراد میدانیم: ۱. آقای رابینسون در دیترویت زندگی میکند. ۲. راننده در میانه راه شهرهای دیترویت و میشیگان زندگی میکند. ۳. درآمد سالانه آقای جونز دقیقاً برابر ۲۰۰۰۰ دلار است. ۴. اسمیت یکبار در بازی بیلیارد از مکانیک برده است. ۵. همسایه دیواربهدیوار راننده یكی از سه مسافر گفته شده است كه دقیقاً سه برابر راننده درآمد دارد. ۶. مسافری كه در شیکاگو زندگی میکند همنام با راننده است. نام مهندس چیست؟ | ||||||||||
| ۴. | كارمندان یك شركت اعتباری مالی عبارتاند از آقای بلك، آقای وایت، خانم كافی، دوشیزه آمبروز، آقای كلی، و دوشیزه ارنشاو. شغل آنها در شركت و البته نه لزوماً به ترتیب اسامی آمده شده عبارت است از مدیر، معاون، صندوقدار، تندنویس، تحویلدار، و منشی. معاون پسر بزرگ مدیر است. منشی داماد تندنویس است. آقای بلك مجرد است. آقای وایت بیستودوساله است. خانم آمبروز خواهراندر تحویلدار است. آقای كلی همسایه مدیر است. شغل هر یك را تعیین نمایید. | ||||||||||
| ۵. | تورلی توسط یك باند تبهكار به خاطر عقب افتادن پرداختهای خود به قتل رسید. بازرس ویژه قتل پس از تحقیق، پنج مظنون را توقیف و از آنان خواست تا هرچه در این باره میدانند بگویند. هریك از مظنونان سه گزاره گفتند كه دوتای آن درست و یكی نادرست است. گزارههای آنها بهقرار زیر است:
حل: برای دیدن حل کلیک کنید :[←] | ||||||||||
| ۶. | آقای شولتز، خواهر او، و همچنین دختر و پسر وی علاقهمند به بازی گلف هستند و اغلب نیز باهم بازی میکنند. گزارههای زیر درباره آنها درست است. آ. بدترین بازیكن و قل بهترین بازیكن از جنس مخالف هستند. ب. بهترین بازیكن و بدترین بازیكن هم سن هستند. چه كسی بهترين بازیکن است؟ | ||||||||||
| ۷. | دانیل کیل رین در یک جاده خلوت در ۲ مایلی پونتیاک در ایالت میشیگان در ساعت 10:30صبح 17 مارس سال گذشته کشته شد. اُتو، کرلی، اسلیم ، میکی و کید یک هفته بعد در دیترویت دستگیر و مورد بازپرسی قرار گرفتند. هر یک از این پنج نفر چهار گزاره گفتند که سهتا از آنها درست و دوتای دیگر نادرست بودند. یکی از آنها کیل رین را کشته است.
چه کسی کیل رین را کشت؟ | ||||||||||
| ۸. |  یك صفحه شطرنجی دارای هشت سطر و هشت ستون با خانههای یکدرمیان قرمز و سفید را در نظر بگیرید. یك مكعب مستطیل چوبی را نیز در نظر بگیرید كه میتوان آن را طوری روی این صفحه قرارداد تا بهطور دقیق و كامل فقط دو خانه مجاور هم را بپوشاند. روشن است كه دقیقاً ۳۲ مهره از این مكعب مستطیلها نیاز است تا تمام خانههای شطرنج پوشانده شوند. اكنون فرض كنید كه فقط ۳۱ مهره مكعب مستطیلی در اختیارداریم تا صفحه شطرنجی را پوشانده. بنابراین، و بهناچار دو خانه نپوشیده باقی خواهند ماند. آیا میتوان طوری صفحه شطرنج را با این ۳۱ مهره مكعب مستطیلی پوشاند كه دو خانه نپوشیده عبارت باشند از اولین خانه سمت چپ اولین سطر و دیگری آخرین خانه سمت راست آخرین سطر؟ اگر میتوان چگونه؟ و اگر نمیتوان چرا؟ | ||||||||||
| ۹. | در همان جامعه خیالی تمرین یك، تازهوارد غریبهای سه نفر از افراد بومی را ملاقات كرده و از آنان میپرسد: "چند نفر از شما سیاستمدار هستید؟". اولین بومی میگوید: "ما همگی سیاستمدار هستیم." بومی دوم میگوید: "نه، فقط دوتا از ما سیاستمدار هستند." بومی سوم میگوید: "هیچکدام درست نگفتند." آیا بومی سوم سیاستمدار است؟ | ||||||||||
| ۱۰. | اتاقی را با چهار دیوار در نظر بگیرید كه یك میخ در مركز هر دیوار كوبیده شده است، بعلاوه در كف و سقف اتاق نیز یك میخ كوبیده شده است. بنابراین، درمجموع شش میخ كوبیده شده در این اتاق وجود دارد. میخها توسط رشته نخهایی به هم متصل شدهاند، هر میخ توسط یك رشته نخ جدا به تمام میخهای دیگر متصل شده است. این رشته نخها به دورنگ آبی و قرمز هستند و هیچ رنگ دیگری در میان نیست. روشن است كه این رشته نخها تعداد زیادی مثلث درست میکنند، میتوان هر دسته سهتایی از این میخها را بهعنوان سه رأس یك مثلث در نظر گرفت. آیا میتوان رنگ رشته نخها را طوری انتخاب كرد که هیچ مثلثی دارای سه ضلع(رشته نخ) همرنگ نباشد؟ اگر میتوان چگونه؟ و اگر نمیتوان چرا؟ | ||||||||||
| ۱۱. | چالش برای خواننده: برای حل مسئله پایانی این قسمت باید مجموعهای از استدلال را تشكیل داد، به قسمی كه هرکدام پشتیبان بعدیهای خود باشد. گرچه آسان نیست، اما كوشش برای حل آن در توان شما هست و البته تلاش شادیآور نیز است. دوازده گوی فلزی در اختیار داریم كه ازهرجهت شبیه هم بوده بهجز یكی كه فقط ازنظر وزن از بقیه متفاوت است ولی سنگینتر یا سبکتر بودن آن نسبت به یازده گوی دیگر مشخص نیست. یك ترازو دوكفهای نیز در اختیارداریم. مسئله از ما میخواهد تا فقط با سه بار توزین این گوی ناجور را مشخص و بعلاوه سنگینتر بودن یا سبکتر بودن آن را نسبت به بقیه نیز نشان دهیم. راهنمایی: برای دیدن راهنمایی کلیک کنید :[←] |
