یادآور و گزیده گزاره‌های کتگوریک (حملی)

گزاره‌های حملی (منطق قیاسی)

درآمد به منطق خلاصه فصل ۶

این قسمت مرور سریع است بر گزاره‌های حملی /Categorical Propositions در تعبیر مدرن و سنتی (آنچه در قسمت‌ها ۱ تا ۸ فصل ششم آمده.) گزاره‌های حملی در کتب منطق قدیم به زبان فارسی به قضیه‌های حملی (قضایای حملیه) موسوم هستند.

۹.۶ یادآور و گزیده گزاره‌های کتگوریک (حملی)

سرنویس

صورت کلی گزاره‌های حملی

کمیت، کیفیت و توزیع شدگی

استنتاج‌ بیواسطه و بواسطه

استنتاج بی‌واسطه بیشتر

نمودار ون برای گزاره‌های حملی

■ گزاره‌های حملی استاندارد ساخت

شِمای کلی گزاره‌های حملی (نیز در کتب منطق قدیم مشهور به قضیه‌های حملی) استاندارد ساخت:
سور حد موضوع حد محمول پیوند.

صورت گزاره	نام و گونه	مثال
همه P - S است،	A (موجب کلی)	همه وکلا آدم‌های ثروتمند هستند.
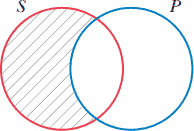
موجب کلی: همه وکلا آدم‌های ثروتمند هستند.
هیچ P - S نیست،	E (سالب کلی)	هیچ مجرم شهروند خوب نیست.
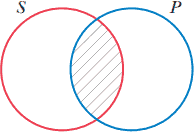
سالب کلی: هیچ مجرم شهروند خوب نیست.
بعضی P - S است،	I (موجب جزئی)	بعضی مواد شیمیایی سمی هستند.
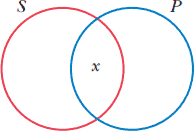موجب جزئی: بعضی مواد شیمیایی سمی هستند.
بعضی P - S نیست،	O (سالب جزئی)	بعضی حشرات آفت نیستند.
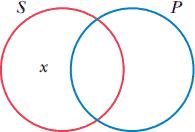سالب جزئی: بعضی حشرات آفت نیستند.

■ کمیت، کیفیت و توزیع شدگی در گزاره‌های حملی

کمیت، کیفیت، و توزیع‌پذیری
گزاره	نام نمادین	کمیت	کیفیت	توزیع‌شد‌گی توسط گزاره
همه P - S است.	A	کلی	موجب	فقط S
هیچ P - S نیست.	E	کلی	سالب	S و P
بعضی P - S است.	I	جزئی	موجب	هیچ‌کدام
بعضی P - S نیست.	O	جزئی	سالب	فقط P

■ جدول توزیع شدگی در گزاره‌های حملی

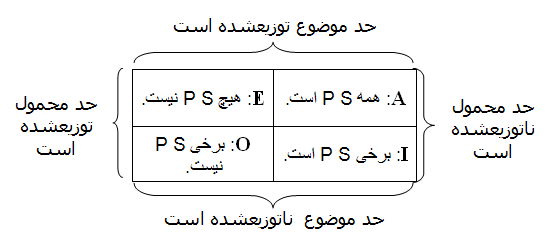
توزیع پذیری قضایای حملی

■ مربع تقابل سنتی

آ. متناقض‌ها:

دو گزاره متناقض هستند هرگاه یکی انکار یا نقض دیگری باشد— به‌عبارت‌دیگر، آن‌ها نتوانند هردو باهم درست و هردو باهم نادرست باشند. دو گزاره حملی استاندارد-ساخت که دارای حد موضوع و حد محمول یکسان، ولی در کمیت و نیز در کیفیت (در هردو) متفاوت‌اند، متناقض‌اند.

ب متضادها:

دو گزاره متضاد هستند اگر هردو نتوانند درست باشند— به‌عبارت‌دیگر، هرگاه درستی یکی مستلزم نادرستی دیگری باشد. مطابق با برآورد سنتی از گزاره‌های حملی، گزاره‌های کلی (A و E) که دارای موضوع و محمول یکسان هستند، ولی در کیفیت (یکی موجب و دیگری سالب) متفاوت‌اند، گزاره‌های متضاد هستند. این تفسیر ارسطویی دارای برخی پیامدهای مسئله‌ساز است. برای توضیح بیشتر به این‌جا و این‌جا نگاه کنید.

ج. داخل در تحت تضاد:

دو گزاره را داخل در تحت تضاد گویند اگر هردو نتوانند نادرست باشند، گرچه ممکن است هردو درست باشند. بنا بر تفسیر سنتی، گزاره‌های جزئی (I و O)، که دارای حدهای موضوع و محمول یکسان ولی در کیفیت متفاوت‌اند (یکی موجب و دیگری سالب)، داخل در تحت تضاد هستند. گفته‌شده، گزاره I "بعضی الماس‌ها سنگ‌های گران‌بها هستند"، و گزاره O "بعضی الماس‌ها سنگ‌های گران‌بها نیستند"، می‌توانند هردو درست باشند— اما نمی‌توانند هردو نادرست باشند و بنابراین باید آن‌ها را داخل در تحت تضاد در نظر گرفت. مشکل مشابه با آنچه در بالا دیدیم اینجا نیز نمایان می‌گردد. برای توضیح بیشتر به این‌جا نگاه کنید.

د. تداخل:

گزاره‌های متناظر:

هرگاه دو گزاره(حملی) در حدهای موضوع و محمول یکسان و در کیفیت نیز یکسان باشند(هردو موجب یا هردو سالب) ولی در کمیت متفاوت باشند(یکی کلی و دیگر جزئی)، آنان را دو گزاره متناظر گویند.

این نیز آن‌گونه که به‌طور سنتی به‌کاربرده می‌شود صورتی از تقابل است. این تقابل بین گزاره‌های کلی و گزاره‌های متناظر جزئی آن‌ها تداخل نامیده شده است. در هر زوج از گزاره‌های نظیر، گزاره کلی را متداخل محیطی و گزاره جزئی را متداخل محاطی می‌نامند.

ه. مربع تقابل:

به چهار طریق گزاره‌ها می‌توانند متقابل باشند— به‌عنوان تناقض، تضاد، داخل در تحت تضاد و به‌عنوان تداخل (محاطی و محیطی). آن‌ها توسط یک نمودار مهم و بسیار مورد کاربرد بنام مربع تقابل نمایش داده می‌شوند. این نمودار در شکل ۱-۶ نمایش داده شده است:

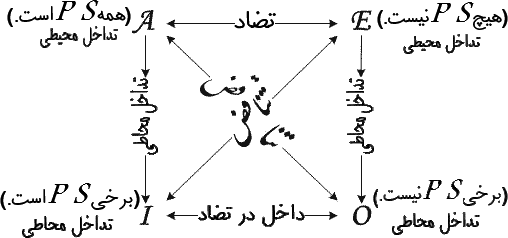
ک. استنتاج‌های بی‌واسطه و به‌واسطه:

عقیده بر آن بود که روابط نشان داده در مربع تقابل مبنایی جهت اعتبار شکل‌های مقدماتی و خاص از استدلال هستند. برای توضیح آن‌ها ابتدا باید استنتاج بی‌واسطه و استنتاج به‌واسطه را از هم تمیز دهیم. وقتی نتیجه‌ای‌ را از یک یا تعداد بیشتر مقدمه استخراج می‌کنیم، آنگاه می‌باید استنتاجی حضور داشته باشد. هرگاه پای بیش از یک مقدمه در میان باشد (آن‌گونه که در قیاس است) این استنتاج را به‌واسطه می‌گویند، زیرا نتیجه از مقدمه اول و به‌واسطه مقدمه دوم به‌دست‌آمده است. اما وقتی نتیجه فقط از یک مقدمه حاصل آمده باشد، آنگاه پای چنین واسطه‌ای در میان نخواهد بود، و در این حالت آن را استنتاج بی‌واسطه می‌گویند.

ک. استنتاج‌های بی‌واسطه بیشتر:

اگر . . .		آنگاه خوهیم داشت . . .
A درست فرض شده باشد.		E نادرست، I درست، O نادرست است.
E درست فرض شده باشد.		A نادرست، I درست، O نادرست است.
I درست فرض شده باشد.		E نادرست است، A و O نامعین هستند.
O درست فرض شده باشد.		A نادرست است، E و I نامعین هستند.
A نادرست فرض شده باشد.		O درست است، E و I نامعین هستند.
E نادرست فرض شده باشد.		I درست است، A و O نامعین هستند.
I نادرست فرض شده باشد.		A نادرست، E درست، O درست است.
O نادرست فرض شده باشد.		A درست، E نادرست، I درست است.

■ استنتاج‌های بی‌واسطه وارون

آ. عکس مستوی / وارون ساده:

عکس مستوی [مستوی:هموار] (یا وارون ساده) استنتاجی است که از جابجایی حد موضوع و حد محمول یک گزاره به دست آید. "هیچ مردی فرشته نیست" به "هیچ فرشته‌ای مرد نیست" در جدول زیر تمام این نوع استنتاج‌های بی‌واسطه را، آن‌گونه که در منطق سنتی فهمیده می‌شود، آورده‌ایم:

عکس مستوی معتبر
گزاره اصلی		عکس مستوی
A: همه P ،S است.		I: بعضی S ،P است. (توسط تحدید)
E: هیچ P ،S نیست.		E: هیچ S ،P نیست.
I: بعضی P ،S است.		I: بعضی S ،P است.
O: بعضی P ،S نیست.		(عکس مستوی معتبر نیست)

ج. عکس متمم:

برای ساختن عکس ‌متمم‌ یک گزاره، کیفیت آن را تغییر داده (موجبه به سالبه یا سالبه به موجبه) و حد محمول را با متمم آن جایگزین می‌کنیم. اما حد موضوع و همچنین کمیت گزاره را بدون تغییر باقی می‌گذاریم. در جدول زیر انواع برگردان‌های ‌متمم‌ نشان داده‌شده است.

عکس متمم
گزاره اصلی		عکس متمم
A: همه P ،S است.		E: هیچ S غیرP نیست.
E: هیچ P ،S نیست.		A: همه S غیرP است.
I: بعضی P ،S است.		O: بعضی S غیرP نیست.
O: بعضی P ،S نیست.		I: بعضی S غیرP است.

د. عکس نقیض:

برای ساختن گزاره عکس ‌نقیض حد موضوع را با متمم حد محمول، و حد محمول را با متمم حد موضوع جابجا می‌کنیم. کیفیت و کمیت دست‌نخورده باقی می‌مانند. بنابراین، عکس نقیض یک گزاره A یک گزاره A و عکس نقیض یک گزاره O یک گزاره O است و بقیه نیز به‌همین ترتیب‌اند. عکس نقیض را می‌توان به یعنی عکس مستوی و عکس متمم کاهش داد. در جدول زیر انواع عکس نقیض نشان داده‌شده است.

عکس نقیض
گزاره اصلی		عکس نقیض
A: همه P ،S است.		E: همه غیرP غیرS است.
E: هیچ P ،S نیست.		O: بعضی غیرP غیرS نیست. (توسط تحدید)
I: بعضی P ،S است.		(عکس نقیض معتبر نیست )
O: بعضی P ،S نیست.		O: بعضی غیرP غیرS نیست.

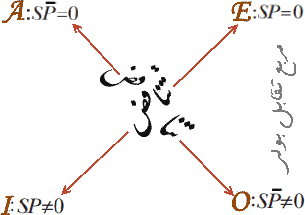
مربع تقابل بولی:

■ نمایش نمادین و نمودار ون برای گزاره‌های حملی:

صورت	گزاره	نمایش نمادین	شرح
A	همه P ،S است.	0=SP̄	طبقه چیزهایی که S و غیرP هستند خالی است.

E	هیچ P ،S نیست.	SP=0	طبقه همه‌چیزهایی که S و P هستند خالی است.

I	بعضی P ،S است.	SP≠0	طبقه همه‌چیزهایی که S و P هستند خالی نیست.(SP حداقل یک عضو دارد.)

O	بعضی P ،S نیست.	0 ≠SP̄	طبقه چیزهایی که S و غیر-P هستند خالی نیست. (SP̄ حداقل یک عضو دارد.)