قیاس و قیاس حملی
قیاس حملی (منطق قیاسی)
درآمد به منطق فصل ۷ قسمت ۱
در فصل قبل بطور گسترده با گزارههای کتگوریک (حملی) آشنا شدیم. گونهای از استدلال استنتاجی، بنام قیاس (Syllogism)، هست که فقط دارای سه عبارت گزارهای (دو مقدمه و یک نتیجه) است. به قیاسی که هر سه گزاره آن کتگوریک باشند قیاس کتگوریک (نیز قیاس حملی) گفته میشود. موضوع این فصل (فصل ۷) بررسی اینگونه قیاسها است و این قست آغازی برای شناسایی قیاس حملی و اجزای آن است.
۱.۷ قیاس و قیاس حملی
قیاس حملی
CategoriCal syllogism
یک استدلال استنتاجی که شامل سه گزاره حملی است، بقسمی که همگی باهم دقیقاً دارای سه حد باشند و هر یک از آنها [حدها] دقیقاً در دو گزاره از گزارههای تشکیلدهنده رویداده باشد.
استاندارد-ساخت
Standard form
گفته میشود یک قیاس به ساخت (یا صورت) استاندارد است اگر مقدمات و نتیجه آن همگی گزارههای حملی استاندارد-ساخت (A، E، I یا O) باشند و به ترتیب استاندارد (مقدمه مهاد، مقدمه کهاد و سپس نتیجه) مرتبشده باشد.
حد مِهین
حد اکبر
Major Term
حدی که بهعنوان حد محمول در نتیجه یک قیاس حملی استاندارد-ساخت روی میدهد.
حد کِهین
حد اصغر
Minor Term
حدی که بهعنوان حد موضوع در نتیجه یک قیاس حملی استاندارد-ساخت روی میدهد.
حد وسط
Middle Term
در یک قیاس حملی استاندارد-ساخت (که باید دقیقاً شامل سه حد باشد) آن حدی که در هر دو مقدمه آمده ولی درنتیجه حضور ندارد.
اکنون در جایی هستیم که میتوانیم از گزارههای حملی برای گسترش بیشتر استدلال بهره ببریم. استدلالهایی بر پایه گزارههای A, E, I, O که دارای دو گزاره حملی بهعنوان مقدمات (نامیده به مقدمات قیاس) و یک گزاره حملی دیگر برای نتیجه (نامیده به نتیجه قیاس) هستند. نام اینگونه استدلالها قیاس است، و بهطور کلی، یک قیاس یک استدلال استنتاجی است که در آن نتیجه از دو مقدمه به دست آمده باشد.
قیاسهایی که اینجا مورد توجه ماست حملی (کتگوریک) نام دارند، زیرا آنها استدلالهایی بر مبنای روابط بین کلاسها هستند، روابطی که توسط گزارههای حملی که با آنها آشناییم، بیان میشوند. مشخصتر، یک قیاس حملی را یک استدلال استنتاجی تعریف میکنیم که شامل سه گزاره حملی است، بقسمیکه همگی باهم دقیقاً دارای سه حد باشند و هر یک از آنها [حدها] دقیقاً در دو گزاره از گزارههای تشکیلدهنده رویداده باشد.
قیاسها بسیار معمول، واضح و بهآسانی آزمونپذیرند. دستگاه قیاسهای حملی، که برآنیم تا به کاوش در آن بپردازیم، توانا و ژرف است. لایبنیتس فیلسوف و ریاضیدان قرن هفدهم درباره اختراع صورت قیاسها جنین میگوید "یکی از زیباترین و نیز مهمترین ساختههای ذهن بشر." قیاسها نیروی پیش برنده استدلالها هستند و آنگونه که بهطور سنتی در عمل به کار میرفت ابزاری کارا چه در نوشتن و چه در مباحثات بوده است.
قبل از آنکه به اجزا و ویژگیهای قیاسها بپردازیم بجاست تا مثالی از قیاس را ببینیم. در زیر یک قیاس معتبر حملی استاندارد-ساخت آمده که در ادامه از آن بهعنوان نمونه استفاده خواهیم کرد:
هیچ پهلوان ترسو نیست.
بعضی سربازان ترسو هستند.
بنابراین بعضی سربازان پهلوان نیستند.
قیاس حملی استاندارد-ساخت:
برای تحلیل دقیق یک چنین استدلال نیاز است تا استدلال به صورت [ساخت] استاندارد باشد. گفته میشود یک قیاس حملی استاندارد-ساخت است (همانطور که مثال بالا چنین است) هرگاه دو مورد درباره آن درست باشد:
(آ) مقدمات و نتیجه آن همگی گزاره حملی استاندارد-ساخت (A, E, I یا O) باشند؛ و
(ب) آن گزارهها به روش قاعدهمند (ترتیب-استاندارد) مرتبشده باشند.
اهمیت این ساخت (صورت) استاندارد هرآینه وقتی آشکار خواهد شد که عهدهدار آزمون اعتبار قیاسها گردیم.
برای توضیح ترتیبی که یک قیاس را به ساخت استاندارد مرتب میکند باید نامهای منطقی مقدمات قیاس و همینطور نامهای منطقی حدهای قیاس و نیز اینکه چرا این نامها — که بسیار مهم و مفید هستند — به آنها منتسب شدهاند را بدانیم. این قدم بعدی ما در تحلیل قیاسات حملی خواهد بود. در این فصل، برای کوتاهی در سخن، به قیاسهای حملی صرفاً "قیاس" خواهیم گفت.
■ الف. حدهای قیاس: مِهین (یا اکبر)، کِهین (یا اصغر) و وسط
سه گزاره حملی در مثال ما در بالا در مجموع دقیقاً دارای سه حد هستند: پهلوانان، سربازان، و ترسوها. برای تشخیص نام حدهای قیاس به نتیجه قیاس نگاه میکنیم که البته دارای دو حد است. نتیجه در مثال ما یک گزاره O است، «بعضی سربازان پهلوان نیستند.» حدی که در نتیجه قیاس بهعنوان محمول حضور دارد (در مثال ما «پهلوانان»)، حد مِهین (یا حد اکبر) قیاس نام دارد. حدی که در نتیجه قیاس بهعنوان موضوع (در مثال ما "سربازان") حضور دارد، حد کِهین (یا حد اصغر) قیاس نام دارد. حد سوم قیاس (در مثال ما "ترسوها") که هرگز در نتیجه حضور نخواهد داشت، اما همیشه در هردو مقدمه حضور دارد، حد وسط نام دارد.
مقدمات قیاس نیز دارای نامهای خود هستند. و این نامگذاری بعد از حضور حدها در آنها انجام میشود. حدهای مهین و کهین هر یک باید در مقدمه متفاوتی حضور داشته باشند. مقدمهای که شامل حد مهین است مقدمه مِهین (همچنین مهاد قیاس یا کبرای قیاس) نام دارد. در مثال ما، "پهلوانان" حد مِهین است بنابراین مقدمهای که شامل "پهلوانان" است— هیچ پهلوان ترسو نیست— مقدمه مِهین است. مقدمه مهین بودن آن به این خاطر نیست که اول آمده است، بلکه فقط به خاطر آن است که شامل حد مِهین است. فارغ از آنکه مقدمات به چه ترتیب نوشته میشدند، این، مقدمه بازهم مهین میبود.
مقدمهای که شامل حد کِهین است مقدمه کِهین [همچنین کهاد قیاس یا صغرای قیاس] نام دارد. در مثال، "سربازان" حد کِهین است بنابراین مقدمهای که شامل "سربازان" است - بعضی سربازان ترسو هستند.- مقدمه کِهین است. مقدمه کهین بودن آن به این خاطر نیست که اول آمده است، بلکه فقط به خاطر آن است که شامل حد مِهین است.
مرور کلی
| اجزای قیاس استاندارد ساخت | |
| حد مِهین | حد محمول نتیجه |
| حد کِهین | حد موضوع نتیجه |
| حد وسط | حدی که در هردو مقدمه آمده ولی در نتیجه نیست. |
| مقدمه مهین (مهاد قیاس) | مقدمهای که شامل حد مهین است. در قیاس استاندارد ساخت مقدمه مهاد همیشه در اول میآید. |
| مقدمه کهین (کهاد قیاس) | مقدمهای که شامل حد کهین است. |
| حدود قیاس | حد مهین (یا حد اکبر)، حد کِهین (یا حد اصغر)، حد وسط |
مقدمه مِهین
مهاد قیاس
کبرای قیاس
مقدمه کبرای
Major premise
در یک قیاس حملی استاندار-ساخت آن مقدمهای که شامل حد مهین است.
مقدمه کِهین
کهاد قیاس
صغرای قیاس
مقدمه صغرا
Minor Premise
در یک قیاس حملی استاندار-ساخت آن مقدمهای که شامل حد کهین است.
ضرب
ضرب قیاس
Mood
یک ویژگی قیاسهای حملی استاندارد-ساخت که بهوسیله ساختهای (صورتهای) گزارههای حملی استاندارد-ساخت مشمول در آن معین میشود. ازآنجاکه فقط چهار ساخت(صورت) گزارههای (A، E، I یا O) وجود دارد و هر قیاس دقیقاً شامل سه گزاره از این نوع است، دقیقاً ۶۴ ضرب وجود دارد. هر ضرب بهوسیله سه حرف گزارههای متشکله آن بهصورت . . . AAA, AAE, AAI, AAO, AEA, AEE, AEI, AEO, AIO و مانند آنها تا OOO مشخص میگردد.
کمی پیشتر گفته شد، یک قیاس دارای ساخت استاندارد است، هرگاه مقدمات آن به روش قاعدهمند (ترتیب-استاندارد) مرتب شده باشند. اکنون میتوان مرتب بودن را توضیح داد: در یک قیاس استاندارد-ساخت، مقدمه مهین نخست، مقدمه کهین دوم، و نتیجه در پایان میآیند. چرائیِ اهمیت این ترتیب بزودی آشکار خواهد شد.
ب. ضرب قیاس
هر قیاس دارای یک ضرب است. ضرب یک قیاس بهوسیله نوع گزارههای حملی استاندارد-ساخت (A, E, I یا O) حاضر در آن قیاس تعیین میشود. بنابراین، ضرب هر قیاس توسط سه حرف نشان داده میشود، و این سه حرف همیشه به ترتیب مشخص (ترتیب-استاندارد) ظاهر میشوند. حرف اول نشاندهنده نوع گزاره مهاد قیاس، حرف دوم نشاندهنده نوع گزاره کهاد قیاس، و حرف سوم نشاندهنده نوع گزاره نتیجه قیاس است. در قیاس مثال بالا، نوع مقدمه مهاد («هیچ پهلوان ترسو نیست») یک گزاره E، مقدمه کهاد («بعضی سربازان ترسوهستند.») یک گزاره I، و نتیجه («بعضی سربازان پهلوان نیستند.») یک گزاره O است. بنابراین ضرب قیاس EIO خواهد بود.

ج. شکل قیاس
ضرب قیاسهای استاندارد-ساخت بهتنهایی صورت منطقی قیاس را مشخص نمیکند. این را میتوان با مقایسه دو قیاس (آ) و (ب) در زیر با ضرب یکسان، که به گونه منطقی بسیار متفاوتاند، دریافت.
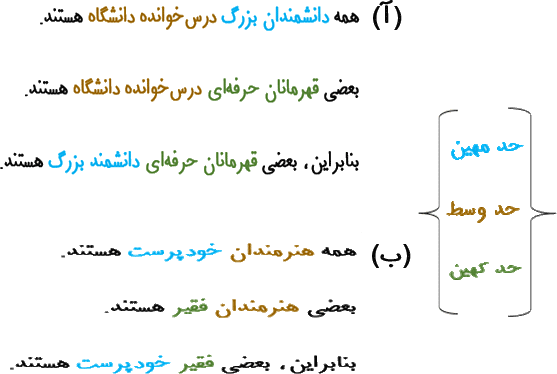
ضرب هر دو قیاس AII است. اما یکی از آنها معتبر و دیگری چنین نیست. تفاوت بین آنها را میتوان با بیشترین آشکاری نشان داد چنانچه سازههای منطقی آنها را بوسیله کوتاه نویسی حدهای کهین با S (موضوع نتیجه)، حدهای مهین با P (محمول نتیجه) و حدهای وسط را با M نشان دهیم. بعلاوه اگر نماد سهنقطه "∴" را بجای "بنابراین" بکار ببریم، آنگاه سازههای این دو قیاس را بهقرار زیر به دست میآوریم:
الف.
همه
M - P است.
بعضی M -
S است.
________________
∴ بعضی
P - S است.
ب.
همه
P - M است.
بعضی S -
M است.
________________
∴ بعضی
P - S است
این دو بسیار متفاوت هستند. در یکی با برچسب الف، حد وسط، M، حد محمول هردو مقدمه است. اما در دیگری با برچسب ب، حد وسط، M، حد موضوع هردو مقدمه است. خواهیم دید که قیاس ب یک استدلال معتبر است؛ ولی قیاس الف معتبر نیست.
این مثالها نشان میدهند گرچه صورت قیاس بهطور جزوی توسط ضرب آن مشخص میشود (AII در هردو حالت بالا)، اما قیاسهایی با ضرب یکسان میتوانند دارای تفاوت مهم در صورتهای خود باشند که بستگی به جای نسبی حد وسط آنها دارد. برای توصیف صورت یک قیاس بهتمامی، ما باید ضرب آن را بیان کنیم (سه حرف سه گزاره) و نیز شکل آنها را — که مراد ما از شکل موقعیت حد وسط در مقدمات است.
قیاسها میتوانند به چهار— و فقط چهار شکل مختلف باشند.
۱. حد وسط میتواند حد موضوع مقدمه وسط و حد محمول مقدمه کهین باشد،
۲. حد وسط میتواند حد محمول هردو مقدمه باشد،
۳. حد وسط میتواند حد موضوع هردو مقدمه باشد،
۴. حد وسط میتواند حد محمول مقدمه مهین و حد موضوع مقدمه کهین باشد.
این در جایگاههای مختلف قرار گرفتن حد وسط، به ترتیب تشکیلدهنده اشکال اول، دوم، سوم، و چهارم قیاس است. هر قیاس باید به یکی از این اشکال باشد. وقتی این اشکال را طبق آرایه زیر (از راست به چپ) شِماتیک کنیم آنوقت خصوصیات آنها آسانتر تجسم مییابد. در رجوع به این آرایه از ضربها صرفنظر شده و نیز سور و رابطه نشان داده نشدهاند— لیکن موقعیت نسبی حدهای قیاس برجسته شدهاند.
|
چهار شکل قیاسهای حملی مقدمات و نتیجه را از چپ به راست بخوانید. |
|
|
M — P
S — M ∴S — P شکل اول |
P — M S — M ∴S — P شکل دوم |
|
M — P M — S ∴S — P شکل سوم |
P — M M — S ∴S — P شکل چهارم |
| P حد مهین (محمول نتیجه)؛ S حد کهین (موضوع نتیجه)؛ M حد وسط (حدی که در هر دو مقدمه میآید) | |
هرگاه ضرب و شکل هر قیاس استاندارد-ساخت را مشخص کنیم آنگاه آن قیاس بهتمامی توصیف میشود. قیاسی را که قبلاً بهعنوان نمونه آوردیم (هیچ قهرمانی ترسو نیست....) در شکل دوم است؛ و حد وسط آن یعنی "ترسوها" محمول هردو مقدمه است و ضرب آن نیز EIO است. بنابراین میتوان آن را بهتمامی بهعنوان قیاسی با صورت EIO-۲ توصیف نمود. همانطور که گفتیم این یک قیاس معتبر است؛ و نیز خواهیم دید هر قیاس معتبر نام مخصوص به خود را دارد. نام این صورت، EIO-۲، فستینو [Festino] است و اصطلاحاً گفته میشود این قیاس "در فستینو" است. مثال دیگری ببینیم:
هیچ P - M است.
همه M - S است.
ـــــــــــــــــــــــــــ
∴هیچ P - S است.
این قیاس در شکل اول است (حد وسط موضوع مقدمه مهاد و محمول مقدمه کهاد است)؛ ضرب آن EAE است. بنابراین میتوان آن را بهتمامی با EAE-۱ توصیف کرد، یک صورت که نام انحصاری آن سلرنت [Celarent] است. هر قیاس با این صورت "در سلرنت" است همانطور که هر قیاس با صورت قبلی "در فستینو" است. و از آنجائی که دانسته است سلرنت (EAE-۱) و فستینو (EIO-۲) معتبر هستند، میتوان نتیجه گرفت که هرگاه با یک استدلال در یکی از این اشکال روبرو شدیم آن نیز معتبر است.
■ شمارش صورتهای قیاس
با کار زدن این ابزارهای تحلیلی میتوان هر قیاس حملی ممکن را با ضرب و شکل آن مشخص کرد. اگر همه ضربهای ممکن را فهرست میکردیم و با {. . . AAA, AAE, AAI, AAO, AEA, AEE, AEI, AEO, AIO} آغاز و ادامه میدادیم تا همه حالات ممکن فهرست شوند، درنهایت ( تا رسیدن به OOO) شصتوچهار (۶۴) ضرب ممکن شمرده میشد. و ازآنجاکه هر ضرب میتواند در یکی از چهار شکل روی دهد، پس میتوان دقیقاً ۲۵۶=۶۴×۴ صورت مختلف از قیاسهای حملی استاندارد-ساخت را مفروض دانست. از این ۲۵۶ صورتهای ممکن، همانگونه که خواهیم دید، فقط تعداد کمی از آنها معتبر هستند. و هریک از این صورتهای معتبر نام خاص خود را دارند که شرح آن در ادامه خواهد آمد.
تمرین
هر یک از قیاسهای زیر را بهصورت استاندارد بازنویسی و ضرب و شکل آن را مشخص نمایید.
روند حل:
گام ۱- نتیجه را تشخیص دهید؛
گام ۲- حد محمول که همان حد مهین/کبرا نتیجه است را مشخص کنید؛
گام ۳- مقدمه مهین[یا مهاد قیاس] که همان مقدمه شامل حد مهین است را تعیین کنید؛ گام ۴- بررسی کنید تا مقدمه دیگر مقدمه کهین[ یا کهاد قیاس] باشد؛ یعنی بررسی کنید که آیا شامل حد مهین، یعنی همان موضوع نتیجه، هست یا نه؛
گام ۵- استدلال را بهصورت استاندارد بازنویسی نمایید: ابتدا مقدمه کبرا، دوم مقدمه صغرا و در پایان نتیجه،
گام ۶- نام ضرب و شکل قیاس را تعیین کنید.
۱- هیچ زیردریاییاتمی کشتیبازرگانی نیست، چون هیچ کشتیجنگی کشتیبازرگانی نیست، و همه زیردریاییهایاتمی کشتی جنگی هستند.
حل:
هیچ زیردریاییاتمی کشتیبازرگانی نیست.
همه زیردریاییهایاتمی کشتیجنگی هستند.
بنابراین هیچ کشتیجنگی کشتیبازرگانی نیست.
گام ۱. نتیجه عبارت است از "هیچ کشتی جنگی کشتیبازرگانی نیست".
گام ۲. "کشتیبازرگانی" بخش محمولی نتیجه است پس حد مهین قیاس نیز هست.
گام۳. مقدمه کبرا[مِهین]، مقدمهای است که شامل عبارت "زیردریاییهای اتمی کشتیبازرگانی نیستند" هست.
گام ۴. مقدمه باقیمانده یعنی، "همه زیردریاییهایاتمی کشتیهایجنگی هستند" ازآنجاکه شامل حد موضوع نتیجه "کشتیجنگی" نیست، مقدمه صغرا[کِهین] است.
گام ۵. صورت استاندارد این قیاس بهقرار زیر است؛
گام ۶. سه گزاره این قیاس به ترتیب عبارتاند از E ،A ،E و حد وسط، یعنی "زیردریاییهای اتمی" حد موضوع هردو مقدمه است، پس قیاس به شکل سوم است. بنابراین ضرب و شکل قیاس عبارت است از: ۳-EAE
۶- همه دیویدی گردانها دارای مکانیسم ظریف و گران هستند، هیچ مکانیسم ظریف و گران مناسب برای بازی بچهها نیست، در نتیجه هیچ دیویدی گردانی مناسب برای بازی بچهها نیست.
۷- همه نوجوانان خلافکار افراد ناسازگار هستند؛ و بعضی نوجوانان خلافکار حاصل یک زندگی ازهمپاشیده هستند؛ بنابراین بعضی افراد ناسازگار حاصل زندگیهای ازهمپاشیده هستند.
۸- هیچ فرد سرسخت که حاضر به پذیرش اشتباه نیست معلم خوب نیست، و ازآنجاکه بعضی از افراد دانا افرادی سرسخت هستند که حاضر به پذیرش اشتباه نیستید، پس بعضی معلمهای خوب افراد دانا نیستند.
۹- همه پروتئینها ترکیبات آلی هستند، لذا همه آنزیمها پروتئین هستند، چون همه آنزیمها ترکیبات آلی هستند.
۱۰- هیچ اتومبیل مسابقه برای راندن در سرعت معمولی نیست، اما همه اتومبیلهایی که برای خانوادهها ساخته میشود برای راندن در سرعت معمولی است، ازآنچه گفته شد برمیآید که هیچ اتومبیل مسابقه برای خانواده ساخته نشده است.
حل:
گام ۱. نتیجه عبارت است از: هیچ اتومبیل مسابقه برای خانواده ساخته نشده است.
گام ۲. حد مهین: اتومبیلهایی که برای خانوادهها ساخته میشود.
گام ۳. مقدمه مِهین: همه اتومبیلهایی که برای خانوادهها ساخته میشود وسیلهنقلیه برای راندن در سرعت معمولی است.
گام ۴. مقدمه کِهین: هیچ اتومبیل مسابقه وسیلهنقلیه برای راندن در سرعت معمولی نیست.
گام ۵. صورت استاندارد این قیاس بهقرار زیر است؛
همه اتومبیلهایی که برای خانوادهها ساخته میشود وسیلهنقلیه برای راندن در سرعت معمولی است.
هیچ اتومبیل مسابقه وسیلهنقلیه برای راندن در سرعت معمولی نیست .
بنابراین هیچ اتومبیل مسابقه وسیلهنقلیه برای خانواده ساخته نشده است.
گام ۶. سه گزاره این قیاس به ترتیب، از چپبر است، عبارتاند از A ،E ،E. حد وسط، یعنی "وسیلهنقلیه برای راندن در سرعت معمولی" حد محمول هردو مقدمه مهین و کهین است، پس قیاس در شکل دوم است. بنابراین ضرب و شکل قیاس عبارت است از: ۲-AEE.
