تکنیک نمودار ون در آزمون قیاس

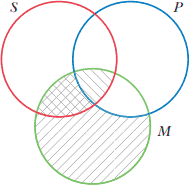
در فصل قبل چگونگی بکار گرفتن نمودارهای دودایره‌ای ون را برای نمایش گزاره‌های حملی یکنوا-ساخت توضیح دادیم. برای آنکه بتوان از نمودار‌های ون برای آزمون قیاس بهره برد، باید هر دو مقدمه قیاس در یک نمودار نشان داده شود. برای این کار نیاز به‌رسم سه دایره همپوشان (دوبه‌دو متقاطع) است، زیرا دو مقدمه قیاس دارای سه حد مختلف هستند، یعنی: حد کِهین، حد مِهین و حد وسط. این حد‌ها را بطور کوتاه شده و به ترتیب با P، S و M نشان می‌دهیم. ابتدا دو دایره برای نشان دادن فقط یک گزاره تکی رسم، و سپس دایره سومی را در پایین آن‌ها بقسمی که با هردو دایره رسم شده قبلی همپوشانی داشته باشد رسم می‌کنیم. این سه دایره را به ترتیب با S و P و M برچسب دار کرده. بهمان شیوه که دایره رسم شده با برچسب S نشان‌دهنده دو کلاس S و S̄ خواهد بود، دو دایره همپوشان رسم‌شده یا برچسب‌های S و P چهار کلاس (SP, SP̄, S̄P و S̄P̄) را نشان خواهند داد، و به همین طریق سه دایره رسم شده همپوشان با برچسب‌های P ،S و M نشان‌دهنده هشت کلاس: SP̄M̄, SPM̄, S̄PM̄, SP̄M, SPM, S̄PM, S̄P̄M و S̄P̄M̄ خواهند بود. همان‌طور که در شکل ۱ دیده می‌شود، همه کلاس‌ها با هشت ناحیه که از تقسیم صفحه با سه دایره ایجادشده، نشان داده‌شده‌اند.

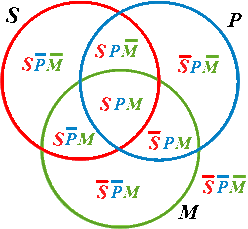
شکل ۱ در بالا را می‌توان برحسب کلاس‌های معینِ مختلف، برای مثال کلاس‌های همه سوئدی‌ها(S)، همه پزشکان(P)، و همه موسیقی‌دان‌ها(M)، تعبیر کرد. SPM ضرب سه کلاس است و حاصل‌ضرب عبارت است از کلاس همه سوئدی‌های پزشک که موسیقیدان هستند. SPM̄ ضرب دو کلاس و متمم کلاس سوم است و حاصل‌ضرب عبارت است از سوئدی‌های پزشکی که موسیقیدان نیستند. SP̄M ضرب کلاس اول و سوم و متمم کلاس دوم است و حاصل‌ضرب عبارت است از سوئدی‌های موسیقیدان غیرپزشک. SP̄M̄ ضرب کلاس اول و متمم دو کلاس دیگر است، یعنی کلاس همه سوئدی‌های غیر موسیقیدان و غیرپزشک. بعدی، یعنی S̄PM ضرب کلاس‌های دوم و سوم با متمم کلاس اول است، یعنی کلاس همه پزشکان موسیقیدان غیر سوئدی. S̄PM̄ ضرب کلاس دوم و متمم دوکلاس دیگر است: کلاس همه پزشک‌هایی که نه موسیقیدان هستند و نه سوئدی. S̄P̄M ضرب کلاس سوم با متمم دو کلاس دیگر است، یعنی کلاس موسیقیدان‌های غیرپزشک و غیر سوئدی. سرانجام S̄P̄M̄ متمم ضرب سه کلاس اصلی است: کلاس همه‌چیزهایی که نه سوئدی و نه موسیقیدان و نه پزشک هستند.

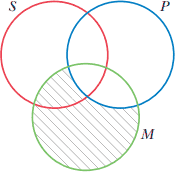
اگر فقط به دو دایره با برچسب P و M توجه کنیم، روشن است که با سایه زدن یا قرار دادن یک x می‌توان هر گزاره حملی استاندارد-ساخت را که دارای حدهای P و M است را، فارغ از آنکه کدام حد موضوع و کدام حد محمول است، نمودار سازی کنیم. بنابراین، برای نمودار ‌سازی گزاره "همه P - M است" ( 0=MP̄) همه M به‌جز آن قسمت که درون P (همپوشان با P است) است را سایه زده. همان‌طور که دیده می‌شود، این ناحیه شامل دو قسمت برچسب دار SP̄M و S̄P̄M است. شکل ۲ این نمودار را نشان می‌دهد.

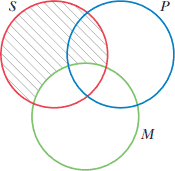
و اگر فقط به دو دایره با برچسب S و M توجه داشته باشیم، روشن است که با سایه زدن یا قرار دادن یک x می‌توان هر گزاره حملی استاندارد-ساخت را که دارای حدهای S و M است را، فارغ از آنکه کدام حد موضوع و کدام حد محمول است، می‌توان نمودار سازی کرد. بنابراین، برای نمودار سازی گزاره "همه M - S است" (0=SM̄)، همه S به‌جز آن قسمت را که درون M (همپوشان با M) است سایه زده. همان‌طور که دیده می‌شود، این ناحیه شامل دو قسمت برچسب دار SPM̄ و SP̄M̄ است. نمودار این گزاره در شکل ۳ دیده می‌شود.

اکنون فایده داشتن سه دایره همپوشان روشن می‌شود و آن اینکه روشی میسر می‌گردد تا بتوان دو گزاره را باهم نمودار سازی کرد— البته با شرایط، یعنی، فقط سه حد متمایز در آن‌ها حضور داشته باشد. بنابراین می‌توان نمودار دو گزاره "هر P - M است" و "هر M - S است" را هردو باهم مطابق شکل ۴ نشان داد.

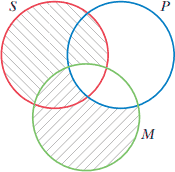
این شکل(شکل ۴) نمودار دو مقدمه قیاس ۱-AAA است:

همه P - M است.
همه M - S است.
ــــــــــــــــــــــــــــــ
∴ همه P - S است.

این قیاس فقط و فقط وقتی معتبر‌ است که دو مقدمه آن مستلزم نتیجه باشند، یعنی هر دو باهم آنچه را بگویند که توسط نتیجه گفته‌شده. بنابراین نمودار سازی مقدمات یک قیاس معتبر ‌باید کفایت نمودار سازی نتیجه آن را نیز نماید، و این باید بدون هیچ علامت‌گذاری بیشتر دایر‌ه‌ها باشد. برای نمودار سازی نتیجه یعنی "همه P S است". باید دو قسمت برچسب‌دار و سایه زده باشد. با بررسی نموداری که دو گزاره مقدمه را نشان می‌دهد، خواهیم دید که نتیجه نیز نمودار سازی شده است. از این واقعیت می‌توان نتیجه گرفت که AAA-۱ یک قیاس معتبر است.[مثل هر قیاس معتبر دیگر این قیاس هم دارای نام است. ضرب آن AAA است زیرا شامل سه گزاره A است، شکل اول است زیرا حد وسط موضوع مقدمه مهاد و محمول مقدمه کهاد است. هر قیاس به این صورت معتبر باربارا (bArbArA) نام دارد. [نام‌ بقیه قیاس‌های معتبر در قسمت ۵ همین فصل خواهد آمد.] اکنون نمودار ون را برای یک قیاس که بطور آشکار نامعتبر است بکار برده:

همه سگ‌ها پستاندار هستند.
همه گربه‌ها پستاندار هستند.
ــــــــــــــــــــــــــــــ
بنابراین همه گربه‌ها سگ هستند.

نمودار هر دو مقدمه در شکل ۵ آمده است.

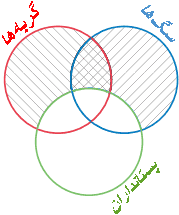
در این نمودار، S مشخص‌کننده کلاس همه گربه‌ها، P مشخص‌کننده همه سگ‌ها و M مشخص‌کننده کلاس همه پستانداران هستند، و بعلاوه قسمت‌های: SPM̄, S̄PM̄ و نیز SP̄M̄ سایه زده شده‌اند. اما نتیجه نمودار سازی نشده است، زیر SP̄M سایه‌زده نشده است, و برای نمودارشدن نتیجه باید SP̄M̄ و SP̄M هردو سایه‌زده می‌شدند. بنابراین مشاهده می‌شود که نمودار سازی دو مقدمه یک قیاس به‌صورت ۲-AAA برای نمودار سازی ‌شدن نتیجه کفایت نمی‌کند. این ثابت می‌کند که نتیجه چیز بیشتری ازآنچه توسط مقدمات بیان‌شده است را می‌گوید. به‌عبارت‌دیگر، نشان می‌دهد که مقدمات مستلزم نتیجه نیستند. اما استدلالی که در آن مقدمات مستلزم نتیجه نباشند نامعتبر است، و بنابراین ثابت می‌شود که قیاس داده‌شده نیز نامعتبر است (بعلاوه ثابت شد که هر قیاس به‌صورت AAA-۲ بی‌اعتباراست.)

در آزمون قیاس به‌وسیله نمودار ون، وقتی قیاس مورد آزمون دارای یک مقدمه کلی و یک مقدمه جزئی است، مهم است که ابتدا مقدمه کلی نمودار سازی شود. بنابراین، در آزمون قیاس AII-۳:

همه هنرمندان خودبین هستند.
بعضی هنرمندان بی‌چیز هستند.
ــــــــــــــــــــــــــــــ
بنابراین بعضی بی‌‌چیزها خودبین هستند.

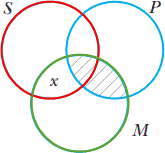
باید قبل از گذاشتن x برای نمودار سازی مقدمه جزئی "بعضی هنرمندان فقیر هستند"، ابتدا مقدمه کلی "همه هنرمندان خودبین هستند" را نمودار سازی کرد. شکل ۶ این مقدمات را که بطور صحیح نموداری شده‌اند نشان می‌دهد.

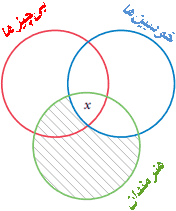
اگر قبل از اينكه ناحیه SP̄M و به دنبال آن ناحیه SP̄M̄ برای نمودار سازی مقدمه کلی نمودار سازی شوند، ابتدا مقدمه جزئی را نمودار سازی کرده بودیم، نمی‌دانستيم كه x را بايد در SPM يا SP̄M يا در هر دو قرارداد. اگر x را در SP̄M يا روي خطي كه آن را از SPM جدا می‌کند قرار می‌دادیم، آنگاه سايه زدن SP̄M موجب می‌شد تا اطلاعاتي كه قرار است در نمودار باشد نامفهوم گردد. اکنون‌که اطلاعات مقدمات در نمودار درج‌شده‌اند، بايد ديد كه آيا نتيجه نيز نمایان است يا نه. اگر نتيجه "بعضي فقيرها خودبین هستند" نمودار سازی شده باشد، x باید درجایی از ناحيه همپوشان توسط دايره‌های "بی‌چیزها" و "خودبين‌ها" باشد. اين ناحيه همپوشان شامل هر دو ناحيه SPM̄ و SPM است، كه هر دو باهم شامل ناحيه SP می‌شوند. اكنون آنچه را كه نتيجه قياس بیان می‌کند در شكل توسط نمودار سازی مقدمات قياس حاصل(نمودار سازی) گردیده؛ بنابراين قياس معتبر خواهد بود.

حال به مثال دیگری پرداخته كه بررسی آن، نكته مهم‌تری را درباره نمودارهای ون به میان می‌آورد. فرض كنید قرار است به آزمون قیاس زیر پرداخته:

همه دانشمندان بزرگ فارغ‌التحصیل دانشگاه هستند.
بعضی قهرمانان حرفه‌ای فارغ‌التحصیل دانشگاه هستند.
ــــــــــــــــــــــــــــــ
بنابراین بعضی قهرمانان حرفه‌ای دانشمندان بزرگ هستند.

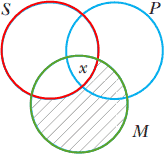
بعدازآنکه در ابتدا با سايه زدن نواحي SPM̄ و S̄PM̄ (شکل ۷) مقدمه كلي را نموداری كرديم،

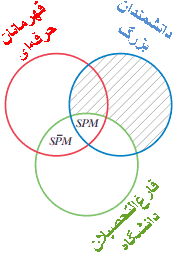
با این معما روبر هستیم که براي نموداری كردن مقدمه جزئی، x را كجا قرار دهیم. با توجه به اينكه مقدمه جزئی عبارت است از "بعضي قهرمانان حرفه‌ای فارغ‌التحصیل دانشگاه هستند،" x بايد درجایی كه دو دايره با برچسب‌های "قهرمانان حرفه‌ای" و " فارغ‌التحصیل دانشگاه" همپوشان هستند، قرار داده شود. اما ناحیه همپوشان خود دارای دو ناحيه: SPM و SP̄M است. پرسش این است که x را بايد در کدام‌یک از آن‌ها قرارداد؟ مقدمات چيزی بما نمی‌گویند، و چنانچه خود تصمیم بگیریم که آن را باید در کدام ناحیه از این‌ دو ناحیه قرار داده، موجب افزودن اطلاعات بیشتری[تصمیم‌گیری توسط ما] ازآنچه در مقدمات است به نمودار می‌کردد. اين باعث خواهد شد كاربرد نمودار به‌عنوان آزمون اعتبار خدشه‌دار گردد. قرار دادن x در هرکدام از آن‌ها موجب فراتر رفتن از مقدمات خواهد شد. اما اگر يك x روي خطي كه ناحيه SM را به دو ناحيه SPM و SP̄M تقسيم كرده قرار دهيم، مقدمه دوم بطور دقيق و بدون افزودن چيزی نمودار می‌شود. قرار دادن يك x روی خط مرزی دو ناحيه، نشان مي‌دهد چيزي هست كه متعلق به يكي از آن‌هاست، ولي مشخص نمی‌کند به کدام‌یک. نمودار كامل شده دو مقدمه در شكل ۸ دیده می‌شود:

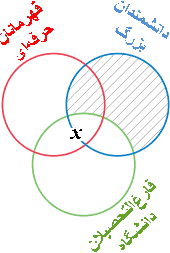
وقتی این نمودار را برسی می‌کنیم تا ببینیم آیا نتیجه در آن نمودار است یا نه، پی می‌بریم كه چنین نیست. برای آنكه نتیجه: یعنی "بعضی قهرمان حرفه‌ای دانشمندان بزرگ هستند" نمودار سازی شده ‌باشد، باید یك x در ناحیه هم‌پوشان دو دایره بالایی، یعنی در SPM̄ یا SPM وجود می‌داشت. اولین از این دو سایه‌زده است و بطورقطع شامل x نیست. بعلاوه، نمودار xای را نیز در SPM نشان نمی‌دهد. این درست است که ‌باید عضوی در SPM̄ و یا SPM وجود داشته باشد، اما نمودار نمی‌گوید در اولی است و در دومی نیست یا برعکس، و تمام آنچه مقدمات می‌گویند، این است که نتیجه ممکن است نادرست باشد. ما نمی‌دانیم که نتیجه نادرست است بلكه فقط می‌دانیم که توسط مقدمات ادعا یا از آن‌ها نتیجه نشده‌ است. این بند آخر كافی است تا بگویم استدلال معتبر نیست. نمودار نه‌تنها برای نامعتبر بودن این قیاس كفایت می‌کند بلكه برای نبود اعتبار برای همه قیاس‌ها به‌صورت ۲-AII نیز كافی است.

مبنای نظری كاربرد نمودارهای ون برای تشخیص قیاس‌های معتبر از نامعتبر چه است؟ جواب به این پرسش شامل دو قسمت است. یکم، همان‌گونه كه در قسمت دوم همین فصل توضیح داده شد، مربوط است به سرشت صوری استدلال‌های قیاسی. در آنجا نشان دادیم كه یك آزمون قابل‌قبول برای اعتبار یا عدم اعتبار یك قیاس تثبیت‌کننده اعتبار یا عدم اعتبار قیاس‌های مختلف با صورت دقیقاً یكسان خواهد بود. این تكنیك مبنای كاربرد نمودارهای ون است. توضیح آنکه چگونه آن‌ها[یعنی نمودارهای ون] به این هدف نائل می‌شوند بخش دوم جواب به پرسش خواهد بود.

بطورمعمول، یك قیاس درباره کلاس‌هایی از چیزهاست كه در آن، همه آن‌ها حاضر و در اختیار نیستند، مثل کلاس موسیقیدانان، دانشمندان بزرگ، یا نمک‌های سدیم و مانند آن‌ها. درباره رابطه شمولیت و یا نبود شمولیت بین این کلاس‌ها ممكن است اقامه دلیل شود که ممکن است [این روابط] بطور تجربی و در دوره‌هایی از بررسی توسط دانشمندان كشف گردند. اما ازآنجاکه همه اعضای این کلاس‌ها هرگز به‌یک‌باره برای بررسی در اختیار نیستند، لذا بطور مسلم قابلیت وارسی مستقیم هم نخواهند داشت. البته می‌توان، به بررسی وضعیتی كه خود ایجاد كرده‌ایم پرداخته، یعنی وضعی كه در آن کلاس‌هایی مدخلیت دارند كه بسیار مشخص فقط چیزهایی هستند كه حاضر و بطور مستقیم برای وارسی گشوده هستند. در این صورت می‌توانیم بطور قیاسی درباره این وضعیت خودساخته بحث کنیم. نمودارهای ون وسایلی هستند برای بیان گزاره حملی استاندارد-ساخت، اما آن‌ها همچنین وضعیت‌های خودساخته ما نیز هستند، یعنی همان الگوهای گرافیكی، یا جوهر به‌جامانده روی كاغذ، یا شیارهای برجسته شده گچ روی تخته؛ و گزاره‌هایی را كه آن‌ها بیان می‌كنند می‌توانند به این‌گونه تعبیر شوند كه آن‌ها به خود نمودارها ارجاع دارند. برای ارائه یك مثال كه می‌تواند به روشن شدن آنچه گفته شد كمك نماید، تصور كنید قیاس ویژه‌ای داریم كه حد‌های آن دلالت بر اقسام مختلف انسان‌های موفق، علاقه‌مند به شغل‌، و توانمند به تمركز كه می‌توانند در سراسر جهان گسترده باشند دارد:

افراد موفق كسانی هستند كه مشتاقانه علاقه‌مند به كارشان هستند.
هیچ‌کس كه مشتاقانه علاقه‌مند به كارش باشد حواسش به‌آسانی ضمن كار پرت نمی‌شود.
ــــــــــــــــــــــــــــــ
بنابراین هیچ‌کس که به‌آسانی حواسش ضمن كار پرت می‌شود آدم موفقی نیست.

شكل این قیاس ۴-AEE است، و می‌توان آن را مطابق زیر به قالب آورد:

همه P M است.
هیچ M S نیست.
ــــــــــــــــــــــــــــــ
∴ هیچ S P نیست.

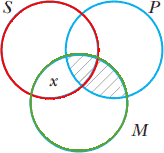
برای آزمون نمودار ون را مطابق شكل ۹ رسم کرده، كه در آن نواحی SPM̄ و S̄PM̄ برای نشان دادن اولین مقدمه سایه‌دار شده‌اند، همچنین SP̄M و SPM به خاطر مقدمه دوم سایه‌دار شده‌اند.

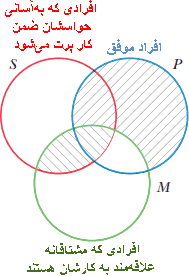
با بررسی این نمودار مشخص می‌شود ناحیه SP (که شامل نواحی SPM و SPM̄ است) سایه‌دار شده است، بنابراین نتیجه قیاس هم‌اکنون نمودار سازی شده است. اكنون، چگونه این نمودار به ما می‌گوید كه قیاس داده‌شده معتبر است؟ این قیاس اشاره به کلاس‌های وسیعی شامل چیزهایی دور از دست است: تعداد زیادی افراد در سراسر جهان هستند که حواسشان به‌آسانی ضمن کار پرت می‌شود. اما، می‌توان به همین صورت قیاسی را ساخت که به اشیایی اشاره کند که در آن برای وارسی در دسترس باشند. این اشیا عبارت‌اند از نقاط واقع در بخش‌های سایه زده نشده دایره‌های با برچسب‌های P ،S و M در نمودار ون. قیاس جدید به‌صورت زیر خواهد بود:

همه نقاط واقع در بخش‌های سایه نزده دایره P نقاطی هستند واقع در بخش‌های سایه نزده‌ دایره M.
هیچ نقطه‌ای واقع در بخش‌های سایه نزده دایره M نقطه‌ای واقع در بخش‌های سایه نزده دایره S نیست.
ــــــــــــــــــــــــــــــ
بنابراین هیچ نقطه واقع در قسمت سایه نزده دایره M نقطه‌ای واقع در بخش‌های سایه نزده دایره S نیست.

این قیاس به هیچ‌چیز غیرقابل‌دسترس اشاره نمی‌کند، و دربار وضعی است که خودساخته‌ایم: یعنی نمودار ون که آن را خود رسم کرده‌ایم. همه قسمت‌ها و همه امکانات برای بررسی شمول وعدم شمول بین کلاس‌ها بی‌واسطه حاضر و بطور مستقیم برای وارسی گشوده هستند. می‌توان همه امکانات را اینجا مشاهده کرد، و ازآنجاکه همه نقاط P نقاط M هم هستند، و M و S نقطه مشترکی ندارند، S و P هم نمی‌توانند نقطه مشترکی داشته باشند. چون در این قیاس فقط به کلاس‌های نقاط واقع در نمودار ارجاع شده است، و با توجه به قابل‌مشاهده بوده همه‌چیزهایی که این قیاس درباره آن‌ها می‌گوید، بطور دقیق مشخص است که قیاس معتبراست. با توجه به اینکه قیاس اصلی درباره افراد دقیقاً به همین صورت قیاس دوم است، با اطمینان و با توجه به سرشت صوری استدلال‌های قیاسی، قیاس اصلی نیز معتبر خواهد بود. توضیحات برای اثبات عدم اعتبار یک قیاس نامعتبر از طریقه نمودار ون بطور دقیق به همین شیوه و یکسان با آن است. بنابراین ما بطور غیرمستقیم به آزمون قیاس اصلی از طریق آزمون مستقیم قیاس دوم پرداخته، که صورت یکسان با آن دارد، اما ارجاع آن به نمودار نشان‌دهنده آن صورت یکسان بود.

منطق دیداری

در نمودار وِن x را کجا باید قرارداد؟

در نمودار وِن برای نمایان‌سازی قیاس‌های حملی، سه حد قیاس (حد موضوع: Subject، حد محمول: Predicate، حد وسط: Middle) با سه دایره به‌هم‌پیوسته به ترتیب با برچسب‌های P، S و M نمایش داده می‌شوند.

وقتی برای یکی از مقدمات قیاس نیاز است تا یک x روی خط‌های یک نمودار ون مانند بالا قرار داده شود، ممکن است پرسیده: روی کدام خط؟ و چرا؟ جواب: x همیشه روی خطی از دایره‌ای گذاشته می‌شود که کلاس نسبت داده‌شده به آن دایره در آن مقدمه نیامده باشد.

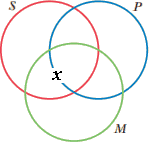
مثال: فرض کنید مقدمه: "بعضی M S است" داده‌شده. در اینجا نمی‌توان مشخص کرد که آیا x به‌عنوان نشان‌دهنده "بعضی" یک P است یا یک P نیست‌ ـــ پس، x آن‌گونه که در شکل زیر می‌توان ‌دید، روی خط دایره P قرار خواهد گرفت:

مثال دیگر: فرض کنید مقدمه: "بعضی P M نیست" داده‌شده. در اینجا نمی‌توان مشخص کرد که آیا آن M که P نیست یک S است یا یک S نیست ـــ پس، x آن‌گونه که در شکل زیر می‌توان‌ دید، روی خط دایره S قرار خواهد گرفت:

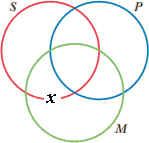
تمرین

آ: با انتخاب برچسب‌های S و P به‌عنوان حد موضوع و حد محمول نتیجه، و M به‌عنوان حد وسط، هر یک از قیاس‌های زیر را به‌تفصیل شرح دهید . ( اگر به قالب‌های چهار شکل قیاس نیاز دارید به ابتدای قسمت ۵ همین فصل(اشکال چهار گانه قیاس) رجوع نمایید.

۱. AEE-۱

حل:

چون گفته‌شده قیاس به شکل اول است، بنابراین حد وسط آن یعنی M حد موضوع مقدمه کهاد است. (قالب‌های قیاس را در ۷-۱ مشاهده نمایید). نتیجه قیاس یک گزاره E است و بنابراین در قالب "هیچ P S نیست" خواهد بود. مقدمه اول(مقدمه مهاد) که شامل حد محمول نتیجه است، یک گزاره A است و بنابراین در قالب "همه P M است" خواهد بود. مقدمه دوم(کهاد) که شامل حد موضوع نتیجه است یک گزاره E است، و بنابراین در قالب "هیچ M S نیست" خواهد بود. ازآنچه گفته شد برمی‌آید که این قیاس به گونه زیر است:

همه P M است.
هیچ M S نیست.
ــــــــــــــــــــــــــــــ
هیچ P S نیست.

آزمون آن توسط نمودار ون در شکل ۷ آمده است و نشان می‌دهد که قیاس معتبر نیست.

۱۴. OAO–۴	۱۰. IAI–۴	۶. OAO–۲	۲. EIO–۲
*۱۵. EIO–۱	۱۱. AOO–۳	۷. AOO–۱	۳. OAO–۳
	۱۲. EAE–۱	۸. EAE–۳	۴. AOO–۴
	۱۳. IAI–۱	۹. EIO–۳	*۵. EIO–۴

حل ۵
معتبر EIO-۴ فریسیسون Fresison		هیچ P M نیست. بعضی S M است. ـــــ ∴ بعضی P S نیست.
حل ۱۰
معتبر IAI–۴ دیماریس Dimaris		بعضی M P ایست. همه S M است. ـــــ ∴ بعضی P S است.
حل ۱۵
معتبر EIO–۱ فریو Ferio		هیچ P M نیست. بعضی M S است. ـــــ ∴ بعضی P S نیست.

ب: هریک از قیاس‌های زیر را به قالب‌های استاندارد درآورده، ضرب و شکل آن‌ها را نام‌برده، و اعتبارشان را به‌وسیله نمودارهای ون بیازمایید.

*۱. بعضی آرمان‌گراها فناتیک هستند، زیرا همه اصلاح‌طلبان آرمان‌گرا هستند و بعضی اصلاح‌طلبان فناتیک هستند.

۲. بعضی فیلسوف‌ها ریاضی‌دان هستند؛ چون بعضی دانشمندان فیلسوف هستند و همه دانشمندان ریاضی‌دان هستند.

۳. بعضی پرندگان عقاب نیستند، زیرا هیچ عقابی سیمرغ نیست و همه سیمرغ‌ها پرنده هستند.

۴. بعضی روان‌پریش‌ها زیان ‌رسان نیستند، اما همه مجرمان زیان رسان هستند، و بنابراین بعضی روان پریشان مجرم نیستند.

*۵. همه وسایل نقلیه زیرآبی زیردریایی هستند، بنابراین هیچ زیردریایی وسیله نقلیه تفریحی نیست، چون هیچ وسیله نقلیه تفریحی وسیله نقلیه زیرآبی نیست.

۶. هیچ فرد پیش‌گام زیان ‌رسان نیست و همه جنایتکاران زیان ‌‌رسان هستند، پس هیچ جنایتکاری فرد پیش‌گامی نیست.

۷. هیچ موسیقیدانی ستاره‌شناس نیست، همه موسیقیدانان طرفدار فوتبال هستند، درنتیجه هیچ ستاره‌شناسی طرفدار فوتبال نیست.

۷. بعضی مسیحیان متودیست نیستند، زیرا بعضی مسیحیان پروتستان نیستند، و بعضی پروتستان‌ها متودیست نیستند.

۹. هیچ فردی که هدف اولیه او برنده شدن در انتخابات باشد آزادیخواه واقعی نیست، و همه سیاستمداران فعال افرادی هستند که هدف اولیه آن‌ها برنده شدن در انتخابات است که این موجب می‌شود هیچ آزادیخواه واقعی سیاستمدار فعال نباشد.

*۱۰. هیچ فرد سست‌عنصر رهبر کارگری نیست، چون هیچ فرد سست‌عنصر آزادیخواه واقعی نیست، و همه رهبران کارگری آزادیخواهان واقعی هستند.

حل ۱
IAI-۳ معتبر Disamis دیسامیس		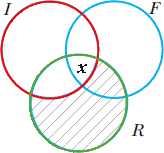بعضی اصلاح‌طلبان فناتیک هستند. همه اصلاح‌طلبان آرمان‌گرا هستند. ـــــ ∴ بعضی آرمان‌گراها فناتیک هستند.
حل ۵
EAE-۴ نامعتبر		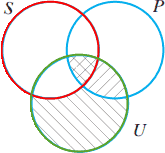هیچ وسیله نقلیه تفریحی وسیله نقلیه زیرآبی نیست. همه وسایل نقلیه زیرآبی زیردریایی هستند ـــــ ∴ هیچ زیردریایی وسیله نقلیه تفریحی نیست.
حل ۱۰
AEE-2 معتبر Camestres کامسترس		همه رهبران کارگری آزادیخواهان واقعی هستند. هیچ فرد سست‌عنصر آزادیخواه واقعی نیست ـــــ ∴ هیچ فرد سست عنصر رهبر کارگری نیست