نمایاندن ۱۵ صورت قیاس‌های حملی معتبر

ضرب قیاس ازجمله ویژگی یک قیاس است که توسط گزاره‌های تشکیل‌دهنده آن (A، E، I، یا O) معین می‌گردد. ۶۴ ضرب مختلف از قیاس حملی و به‌عبارت‌دیگر ۶۴ دسته سه‌تایی از گزاره‌ها: AAA، AAI، AAE، و مانند آن‌ها تا EOO، و OOO وجود دارد.

شکل قیاس یک ریخت منطقی است که توسط جای قرار گرفتن حد وسط در مقدمات مشخص می‌گردد. بنابراین چهار شکل ممکن وجود خواهد داشت که می‌توانند به‌وضوح به فراجنگ آیند اگر نمایش شمایلی این چهار حالت ممکن، آن‌چنان‌که در جدول مرور کلی نمایش ‌داده شده، به خاطر سپرده شوند.

مرورکلی

اشکال چهارگانه قیاس

	شکل اول	شکل دوم	شکل سوم	شکل چهارم
نمایش شماتیک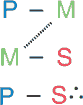
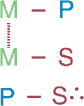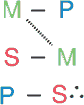شرح	حد وسط موضوع مقدمه مهاد، و محمول مقدمه کهاد است.	حد وسط محمول هر دو مقدمه است.	حد وسط موضوع هر دو مقدمه است.	حد وسط محمول مقدمه مهاد، و موضوع مقدمه کهاد است.

همان‌طور که می‌توان دید:

• در شکل اول: حد وسط موضوع مقدمه کبرا و محمول مقدمه صغرا است.

• در شکل دوم: حد وسط محمول هردو مقدمه است.

• در شکل سوم: حد وسط موضوع هردو مقدمه است.

• در شکل چهارم: حد وسط محمول مقدمه کبرا و موضوع مقدمه صغرا است.

۶۴ ضرب قیاس حملی می‌توانند به‌صورت یکی از چهار ریخت (شکل) ظاهر شوند. ضرب و شکل یک قیاس باهم و به گونه‌ یگانه صورت منطقی آن‌ را معین می‌کنند. بنابراین و به‌طور دقیق (همان‌طور که قبلاً نیز گفته شد) ۲۵۶ (۴×۶۴) صورت ممکن از قیاس حملی استاندارد-ساخت وجود دارد.

بخش زیادی از این صورت‌ها نامعتبر هستند و می‌توان آن‌هایی را که حداقل یکی از قوانین گفته‌شده در قسمت قبل را رعایت نکرده حذف نمود. صورت‌های باقی‌مانده پس از این حذف‌ها تنها صورت‌های قیاسی معتبر خواهند بود. از ۲۵۵ صورت ممکن فقط ۱۵ صورت حذف نخواهند شد و بنابراین معتبر خواهند بود. باید در خاطر بماند که ما تعبیر بولی از گزاره‌های حملی را پذیرفته‌ایم، و طبق آن گزاره‌های کلی (A و E) دارای ویژگی وجودی نیستند. تفسیر کلاسیک از گزاره‌های حملی که مطابق آن طبقه‌ها مورد رجوع توسط گزاره‌ها دارای عضو هستند بعضی از استنتاج‌ها را قابل‌قبول می‌نماید که در اینجا نامعتبر شمرده‌شده‌اند. برای مثال، تفسیر قدیمی‌تر استنتاج تداخل محاطی را از تداخل محیطی روا می‌دارد—مانند: استنتاج گزاره I از گزاره نظیر آن A و همین‌طور استنتاج گزاره O از گزاره نظیر آن E. این نکته تأکیدی است بر آنکه قیاس‌های دیگری (موسوم به قیاس‌های تضعیف‌شده) در اینجا به‌عنوان معتبر در نظر گرفته نشده‌اند. دلایل مقنع برای نپذیرفتن تفسیر قدیمی‌تر به‌طور نسبتاً مفصل در بحث مغالطه وجودی آمده است.

به خاطر آسانی دسترسی به این قیاس‌ها، منطق‌دانان کلاسیک نام‌های یگانه‌ای را به هر قیاس معتبر منسوب کرده‌اند، که هرکدام [از این نام‌ها] به‌تمامی توسط ضرب و شکل آن معین می‌گردد. هنگام کار با استدلال‌های قیاسی، دانستن این مجموعه‌ کوچک از قیاس‌های معتبر و همین‌طور نام آن‌ها بسیار مفید اثر خواهد بود. نام‌ها به‌دقت برگزیده‌شده است و هریک شامل سه حرف صدادار است که ضرب قیاس را مشخص می‌کنند (به همان ترتیب موجود در ساخت استاندارد، یعنی: مقدمه مِهین(کبرا)، مقدمه کِهین(صغرا)، و نتیجه). جایی که قیاس‌‌ معتبری در یک ضرب ولی به شکل‌های مختلف وجود دارد، به هرکدام یک نام یگانه نسبت داده‌اند. برای مثال قیاسی در ضرب EAE و شکل اول Celarent نام‌گذاری شده است، و قیاس معتبر دیگری در همین ضرب، یعنی EAE، در شکل دوم، Cesare نام‌گذاری شده است. اصول جاری برای ساختن این نام‌ها و انتخاب درست حروف صدادار و بی‌صدا، کاملاً حساب‌شده انجام‌گرفته است. بعضی از این قراردادها، همان‌طور که قبلاً گفته شد، در رابطه با قیاس‌های تضعیف‌شده هستند و بنابراین در تعبیر بولی که ما پذیرفته‌ایم قابل‌قبول نیستند. اما بعضی دیگر از این قراردادها پذیرفته‌شده باقی خواهند ماند. برای مثال، حضور حرف s به دنبال حرف صدادار e نشان می‌دهد که وقتی گزاره E به عکس مستوی برگردان شود (همان‌طور که همه گزاره‌های E برگردانده می‌شوند) در همان ضرب به قیاس دیگری در شکل اول تبدیل می‌شود که به‌عنوان بنیادی‌ترین شکل در نظر گرفته‌شده. برای مثال، وقتی مقدمه مِهین(کبرا) Festino، در شکل دوم، به عکس مستوی برگردان شود به Ferio کاسته می‌گردد؛ و Cesare، در شکل دوم، به Celarent کاهش‌یافته و مانند آن‌ها. این امکان‌ها و برگردان‌های دیگر توضیحی است که چرا نام گروه‌های قیاس با حرف بی‌صدای یکسان شروع‌شده‌اند.

هدف از این نام‌گذاری‌ها به ‌کار زدن آن‌ها در عمل بود (و هنوز هم هست.) اگر فردی بداند که بعضی ترکیب‌های مشخص از ضرب و شکل معتبر است، و بعلاوه بتواند معتبرها را به نام تشخیص دهد، آنگاه شایستگی هر قیاس در یک شکل یا ضرب داده شده، تقریباً بلافاصله قابل‌تعیین است. برای مثال ضرب AOO فقط در شکل دوم معتبر است. تنها صورت معتبر AOO-۱ موسوم به باراکو (Baraco) است. فردی که با باراکو آشناست و می‌تواند آن را به‌آسانی تمیز دهد، نیز می‌تواند اطمینان داشته باشد که قیاسی با همین ضرب در تمام اشکال دیگر می‌تواند به‌عنوان نامعتبر رد گردد. یک قیاس باراکو را برای مثال در اینجا آورده:

همه ریاضی‌دانان خوب دارای اندیشه خلاق هستند.
بعضی تحصیل‌کرده‌ها دارای اندیشه خلاق نیستند.
بنابراین بعضی تحصیل‌کرده‌ها ریاضی‌دان خوب نیستند.

فرد با تمرین می‌تواند هماهنگی موجود در قیاس‌‌های مختلف به صورت‌های معتبر را دریابد. کسی که با باراکو آشناست و می‌تواند آن را به‌آسانی تمیز دهد، می‌تواند مطمئن باشد که قیاسی با این ضرب در هر شکل ظاهرشده دیگر می‌تواند نامعتبر باشد.

ساخت استاندارد قیاس‌های حملی کلید ورود به این سیستم است. روش کارآمد و آسان برای تشخیص تعداد کم قیاس‌های معتبر از میان تعداد زیاد قیاس‌ها میسر و در دسترس است، اما این وابسته بدان است که قیاس مورد ملاحظه به صورت (ساخت) استاندارد باشد(یا بتوان آن‌ را به ترتیب استاندارد) درآورد— یعنی، به ترتیب، مقدمه مِهین، مقدمه کِهین و سپس نتیجه. تشخیص یگانه قیاس معتبر متکی به تشخیص ضرب آن است، و ضرب آن با سه حرف، که مشخص‌کننده سه گزاره آن به ترتیب استاندار است، معین می‌گردد. اگر مقدمات قیاس به ترتیب دیگری در میان گذاشته شود، البته قیاس معتبر باقی می‌ماند و این را می‌توان با استفاده از نمودار‌های ون نشان داد. ولی چیزهای زیادی از دست خواهند رفت. توانمندی ما در شناسایی یگانه قیاس‌ها، و بهره از این شناسایی در درک و دریافت کامل از صورت‌های آن‌ها و آزمون اعتبار تند و آسان آن‌ها، همه بر پایه‌ ساخت استاندارد آن‌ها استوار است.➥

منطق‌دان‌های کلاسیک که این صورت‌ها را مورد مداقه قرار می‌دادند، کاملاً با ساختار و "احساس" منطقی آن‌ها آشنا می‌شدند. این سیستم برازنده و به‌دقت ازکاردرآمده موجب توانایی استدلال‌ کننده در سخنان و نوشتارها در مواجه با قیاس‌ها می‌شد تا بلا‌فاصله به تمیز آنان که معتبر بودند، نائل آید و با اطمینان آن‌ها را که چنین نبودند دریابد. برای قرن‌ها چنین رسم بود تا در دفاع از استحکام برهان ارائه‌شده نام صورت قیاس معتبری را که بکار بسته‌شده بود ذکر نمایند. حتی در بحبوحه یک مباحثه داغ، نام بردن از آن‌ها نشان باسوادی و فراست به‌حساب می‌آمد، و دلیلی بود بر این‌که برهان استنتاجی که به آن تکیه شده است خدشه‌بردار نیست. وقتی نظریه قیاس به‌خوبی جاافتاده شود، این مهارت ابزاری، سودمند و دلپذیر قابل‌گسترش می‌گردد.➥

استدلال قیاسی فراوان بکار گرفته می‌شد و از عمده ابزار ضروری تحصیل‌کردگی به‌حساب می‌آمد، به‌گونه‌ای که ارسطو مفسر اصلی و آموزه‌دار بزرگ آن برای بیش از هزار سال مورد تکریم وستایش قرارگرفته. شرح تحلیلی وی از قیاسات هنوز نام ساده و بی‌پیرایه خود را به همراه دارد: "ارگانون"، به معنی "ابزار".

به‌عنوان دانشجوی این سیستم منطقی سرشار، خبرگی ما در کار با قیاس‌ها‌ ممکن است متوسط فقط باشد— بااین‌وجود، داشتن شرح خلاصه‌ای از همه قیاس‌های معتبر در پیش رو، می‌تواند مفید و مورداستفاده قرار گیرد. پانزده قیاس معتبر تحت تعبیر بولی وجود دارد. در سنت قدیمی‌تر، یعنی وقتی عقیده به این بود که استدلال از مقدمات کلی به نتیجه جزئی روا است، البته تعداد قیاس‌های معتبر (که هرکدام نام یگانه خودشان را هم داشتند) بیشتر از پانزده بود. برای مثال، اگر ممکن بود گزاره I را از گزاره نظیر آن A استنتاج کرد (که به نظر ما خطا است)، آنگاه قیاس معتبر موسوم به باربارا AAA-۱ دارای یک خواهرخوانده قانونی "تضعیف‌شده" موسوم به بارباری (Barbari - AAI-۱) نیز بود. اگر ممکن بود گزاره O را از گزاره نظیر آن E استنتاج کرد (که به نظر ما خطا است)، آنگاه قیاس معتبر موسوم به کامسترسAEE-۲ دارای یک خواهرخوانده قانونی "تضعیف‌شده" موسوم به کامسترپ(Barbari - AEO-۲) نیز بود.

این پانزده قیاس معتبر را می‌توان با توجه به شکل هرکدام به چهار گروه تقسیم کرد:

مرور کلی

پانزده صورت معتبر قیاس‌های حملی استاندارد-ساخت

	صورت	نام لاتین	به فارسی
شکل اول (که در آن حد وسط عبارت است از موضوع مقدمه مِهین و محمول مقدمه کِهین.)
۱-	AAA-۱	Barbara	باربارا
۲-	EAE–۱	Celarent	سلارنت
۳-	AII–۱	Darii	دری
۴-	EIO–۱	Ferio	فریو
شکل دوم (که در آن حد وسط محمول هر دو مقدمه است.)
۵-	AEE–۲	Camestres	کامسترس
۶-	EAE–۲	Cesare	چزاره
۷-	AOO–۲	Baroko	باراکو
۸-	EIO–۲	Festino	فستینو
شکل سوم (که در آن حد وسط از موضوع هر دو مقدمه است.)
۹-	AII–۳	Datisi	داتیسی
۱۰-	IAI–۳	Disamis	دیسامیس
۱۱-	EIO–۳	Ferison	فریسون (فرگوسن)
۱۲-	OAO–۳	Bokardo	بوکاردو
در شکل چهارم ( که در آن حد وسط عبارت است از محمول مقدمه مِهین و موضوع مقدمه کِهین.)
۱۳-	AEE–۴	Camenes	کامنس
۱۴-	IAI–۴	Dimaris	دیماریس
۱۵-	EIO–۴	Fresison	فریسیسن