چهار گونهٔ گزارههای حملی
گزارههای حملی (منطق قیاسی)
درآمد به منطق فصل ۶ قسمت ۳
قسمت پیشین توضیح انگارههای «طبقه / یا
کلاس» و « گزاره حملی» بود و گفته شد گزاره حملی گزارههایی هستند که در تحلیل نسبت دو کلاس بکار میروند، یعنی در تایید یا انکار شمول کلی یا جزئی کلاسی مانند
S (موضوع) در کلاس دیگری مانند
P (محمول).
دراین قسمت افزون بر شناسایی چهار گونهیِ گزارههای حملی،
نمایش نموداری آنها نیز پیگرفته میشود.
۳.۶ چهار گونهٔ گزارههای حملی
گزاره حملی استاندارد-ساخت
Standard-form Categorical Proposition
هر گزاره حملی به صورت:
"همه P
،S است" (موجب کلی)،
"هیچ P ،S نیست" (سالب کلی)،
"بعضی P
،S است" (موجب جزئی)،
"بعضی P ،S نیست" (سالب جزئی).
این چهار گونه به ترتیب بهعنوان گزارههای A, E, I و O شناخته میشوند.
نمودار وِن
Venn diagram
نمایش شمایلی یک گزاره حملی یا یک استدلال بوسیله دایرههای همپوشان بخاطر برنمایاندن صورتهای آنها.
گزاره موجب کلی
گزاره موجبهٔ کلیه
گزاره پذیرنده کلی
Universal Affirmative Proposition
A
یک گزاره حملی استاندارد که مدعیاست تمام یک کلاس مشمول[مندرج] در کلاس دیگری است؛
همه P ،S
است.
گزاره سالب کلی
گزاره سالبهٔ کلیه
گزاره انکاری کلی
Universal Negative Proposition
E
یک گزاره حملی استاندارد که مدعیاست تمام یک کلاس مستثنا از کلاس دیگری است؛
هیچ P ،S
نیست.
چهار و فقط چهار گونه گزاره حملی استاندارد-ساخت [یکنوا پیکر] وجود دارد. در مثالهای زیر هر یک از این چهار گونه آمدهاند:
۱- همه
سیاستمداران دروغگو هستند.
۲- هیچ سیاستمدار دروغگو نیست.
۳-
برخی سیاستمداران دروغگو هستند.
۴- برخی سیاستمداران دروغگو نیستند.
اکنون و بهنوبت به بررسی بیشتر این چهار گونه خواهیم پرداخت:
۱- گزاره موجب کلی (گزاره پذیرنده کلی)
در این قسم از گزارههای حملی ادعا میکنیم که همه یک کلاس درون کلاس دیگر است. "همۀ سیاستمداران دروغگو هستند" یک مثال از این قسم است. این گزاره بیان میکند که هر عضو کلاس "سیاستمداران"، عضو کلاس دیگر "دروغگویان" نیز است. شمایِ (طرحواره) هر گزاره موجب کلی را میتوان به گونه:
همهِ P ،S است.
نوشت، که در آن حروف S و P به ترتیب نشاندهنده حدهای موضوع و محمول هستند. اینگونه گزارهها میپذیرند که رابطه شمول [یا اندراج] بین دو کلاس برقرار است. و این شمول سرتاسری یا بهعبارتدیگر کلی است و گفته میشود همه اعضای S عضو P نیز هستند. گزارههایی با این صورت استاندارد، گزارههای موجب کلی نامیده میشوند. آنها همچنین به گزارههای A نیز موسوماند.
☚: وقتی گزارههای حملی به این صورت استاندارد نوشته شوند، به S حد موضوع و به P حد محمول و بهطورکلی به هر یک از آنها حد گفته میشود. ازاینجهت منطق ارسطویی را منطق حدود نیز میگویند.
گزارههای حملی را بیشتر وقتها با نمودار، توسط دو دایره متقاطع که نمایانگر دو کلاس هستند نشان میدهند. این نمودارها به نمودارهای ون موسوم هستند و نام خود را از جان وِن (۱۹۲۳-۱۸۲۴) منطقدان و ریاضیدان که مبدع آنها بود گرفتهاند. ما در آینده این نمودارها را بهطور کامل بررسی خواهیم کرد و خواهیم دید که آنها در ارزیابی اعتبار استنتاجها بهطور فزاینده مفید هستند. اکنون از آنها برای نشاندادن مفهوم گزارههای حملی به شیوه زیر سود خواهیم برد.
یکی از دو دایره را با حرف S برای موضوع و دیگری را با حرف P برای محمول برچسب دار خواهیم کرد. نمودار یک گزاره از گونه A، که بیانگر "همه P ،S است" دارای بخش سایه زدهای[خط زده] است که خارج از P قرار دارد و نشان میدهد عضوی از S وجود ندارد که عضو P نباشد. بنابراین نمودار گزاره A بهصورت زیر نشان داده خواهد شد:
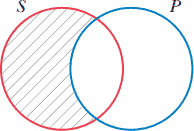
همه P ،S است،
قسمت سایهدار S نشاندهنده آن است که عضوی از S در آن ناحیه وجود ندارد و هر عضوی که در S باشد، باید در قسمت سایه نزده آن باشد که در این صورت عضو P هم خواهد بود.
۲– گزاره سالب کلی: (گزاره انکاری کلی)
در مثال دوم، یعنی "هیچ سیاستمدار دروغگو نیست"، کلاً پذیرفته نمیشود که عضوی از کلاس سیاستمداران عضوی از کلاس دروغگوها است. این گزاره مدعی است که کلاس موضوع، یعنی S، سرتاسر بیرون از رابطه شمول کلاس محمول، یعنی P است. شمایِ گزارههای حملی از این نوع به شیوه زیر نوشته میشود:
هیچ P ،S نیست،
که در آن S و P مثل قبل به ترتیب نمایشدهنده حد کلاس موضوع و حد کلاس محمول هستند. این نوع گزاره، انکار میکند که بین دو حد رابطه شمول وجود دارد و نیز این انکار کلی است. این گزارهها مدعیاند کلاس موضوع، S، بهتمامی مستثنا از کلاس محمول، P است. گزارههایی با این صورت استاندارد، گزارههای سالب کلی نامیده میشوند. آنها همچنین به گزارههای E نیز موسوماند.
در نمودار گزارههای E، این طرد متقابل را با سایهزدن ناحیه همپوشان کلاس S و کلاس P نشان میدهیم.
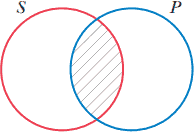
هیچ P ،S نیست،
۳– گزاره موجب جزئی (گزاره پذیرنده جزئی)
سومین مثال فوق یعنی "برخی سیاستمداران دروغگو هستند"، میپذیرد که جزئی از اعضای کلاس سیاستمداران، اعضای کلاس دروغ گویانند. اما این پذیرش سرتاسری نیست. گفتهشده فقط سیاستمداری یا بعضی سیاستمداران دروغگویند. این گزاره پیشنهاد پذیرفتن یا نپذیرفتن چیزی را دربارۀ همۀ سیاستمداران ارائه نکرده و اظهار عقیدهای دربارۀ همه سیاستمداران نمیکند. همچنین نمیگوید که بعضی سیاستمداران دروغگو نیستند، گرچه در برخی زمینهها ممکن است چنین معنائی را در خود داشته باشد. تفسیر لفظی و دقیق این گزاره عبارت از این است که کلاس سیاستمداران و کلاس دروغگویان دارای فرد یا افراد مشترکی در میان خود هستند. این چیزی است که ما از این گزاره استاندارد-ساخت مراد میکنیم.
"بعضی"، یک عبارت نامعین است. آیا معنی آن "حداقل یک" یا "حداقل دو" یا "حداقل چندین" است؟ در گفتگوی روزانه ممکن است زمینۀ گفتگو به دریافت این نکته کمک کند. اما منطق دانان به خاطر استواری و قطعیت "بعضی" را به معنی "حداقل یک"، تعبیر میکنند. شمای یک گزارۀ "موجب جزئی" را میتوان بهصورت زیر نوشت:
بعضی P ،S است،
که میگوید حداقل یک عضو از کلاس مشخصشده توسط حد موضوع S، عضو کلاس مشخصشده توسط حد محمول P نیز هست. این سازه گزارهای میپذیرد که رابطه شمول برقرار است، اما نه به گونه کلی بلکه بهطور جزئی، یعنی فقط در مورد بعضی اعضا یا اعضای خاصی از کلاس اول آن را میپذیرد. گزارههایی با این سازه استاندارد را گزارههای موجب جزئی مینامند. این نوع گزارهها همچنین موسوم به گزارههای I هستند.
در نمودار گزاره I با قرار دادن یک x در ناحیۀ مشترک دو دایره نشانداده میشود که حداقل یک عضو S عضو P هم هست. بنابراین نمودار گزارههای I بهقرار زیر است:
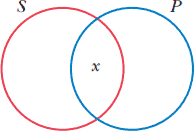
بعضی P ،S است،
۴– گزاره سالب جزئی (گزاره انکاری جزئی)
چهارمین مثال بالا، یعنی "بعضی سیاستمداران دروغگو نیستد"، مانند مثال سوم بهطور سرتاسری اشاره به سیاستمداران ندارد، بلکه فقط به بعضی از افراد این کلاس رجوع میکند؛ و ازاینجهت جزئی است. اما برخلاف مثال سوم شمول برخی از اعضای کلاس اول را در کلاس دوم نمیپذیرد؛ این دقیقاً چیزی است که انکار شده. آن را میتوان به گونه شماتیک بهصورت زیر نوشت:
بعضی P ،S نیست،
که میگوید حداقل یک عضو از کلاس مشخصشده توسط حد موضوعی S خارج از کلاس مشخصشده توسط حد محمولی P است. به گزارههایی که دارای این سازه استاندارد هستند، گزارههای سالب جزئی گفته میشود. آنها همچنین به گزارههای O نیز موسوماند. با قرار دادن یک x در ناحیهای از S که خارج از P است نشان داده میشود حداقل عضوی از S وجود دارد که عضو P نیست. بنابراین نمودار گزارههای O بهقرار زیر است:
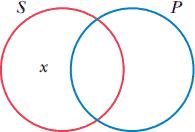
بعضی P ،S نیست،
مثالهایی که در این قسمت بکار بردیم، کلاسهایی بودند که دارای نامهای ساده بودند مانند: سیاستمداران، دروغگوها، گیاهخواران، قهرمانان و مانند آنها. اما حـدود موضوع و محمول در گزارههای استاندارد-ساخت میتواند پیچیدهتر از اینها باشند. برای مثال، در گزاره "همه نامزدهای این جایگاه، افراد شریف و جامعالاطراف هستند"، عبارت "نامزدهای این جایگاه" حد موضوع است و "افراد شریف و جامعالاطراف" حد محمول است. حدهای موضوع و محمول میتوانند از این هم پیچیدهتر شوند، اما هرکدام از این چهار ساخت – استاندارد ، سازندۀ رابطه بین یک کلاس بهعنوان موضوع و یک کلاس بهعنوان محمول خواهند بود. این چهار سازه یعنی گزارههای— I, E, A و O سنگ بنای استدلالهای استنتاجی هستند.
مرور ایجاب (پذیرش) و سلب (ناپذیرش) — کلی (کلی) و جزئی (جزئی)
☚:
به گزارههای A و I گزاره (حملی) ایجابی
و به گزارههای E و O گزارههای (حملی) سلبی میگویند.
☚:
به گزارههای A و E گزاره (حملی) کلی
و به گزارههای I و O گزاره (حملی) جزئی میگویند.
وقتی از قبل تحلیل گزارههای حملی بر ما آشکار است، آنها به نظر ساده و سرراست میآیند. اما کشف نقش بنیادی این گزارهها و نمایانسازی روابط بین آنها قدم بزرگی در توسعه روشمند منطق بهحساب میآید. آنها ازجمله سهم همیشگی ارسطو در دانش بشری خواهند بود. ظاهر ساده آنها گمراهکننده است. منطق دانان بر پایه این بنیاد سازی یعنی کلاسهای اشیا و روابط بین آنها بنیادی را در طی قرون برای تحلیل بسیار ژرف استدلالهای استنتاجی برپا ساختهاند. این سیستم را که باریکاندیشی بهکاررفته در آن، آن را بهعنوان یکی از بزرگترین دستیابیهای اندیش ورزی نشاندار کرده است، در سه مرحله به شرح زیر بررسی خواهیم کرد:
| آ- | در باقیمانده این فصل جنبههای استاندارد سازههای گزارههای حملی، یعنی روابط بین آنها را، ژرفتر توضیح خواهیم داد. نشان خواهیم داد که چه استنتاجهایی را بیواسطه میتواند از این گزارههای حملی استخراج کرد. همانگونه که خواهیم دید، مقدار قابلتوجهی از استدلالهای استنتاجی، بهخودیخود و با فهم کلی از گزارههای A -E - I -O و روابط موجود بین آنها قابلدرک هستند. |
| ب- | در این کتاب، ما قیاس را بررسی خواهیم داد – استدلالهایی که بهطور متعارف باکار گرفتن گزارههای حملی استاندارد-ساخت، ساخته میشوند. ما قلمرو قیاسها را بررسی خواهیم کرد که در آن هر صورت استدلال معتبر به گونه متمایز و با نام مخصوص خود مشخص خواهد گردید. افزون بر آن روشهای توانمند جهت تعیین اعتبار (یا بیاعتباری) قیاسها را گسترش خواهیم داد. |
| ج- | در این کتاب، ما به درآمیختن استدلالهای قیاسی و زبان استدلالی در گفتار روزانه خواهیم پرداخت. در آن فصل همچنین برخی محدودیتهای استدلال بر پایههای این بنیاد را مشخص خواهیم کرد. و درعینحال نگاه کوتاه به نفوذ و وسعت دامنه کاربرد فراهمشده توسط این بنیاد (گزارههای حملی و قیاس) خواهیم انداخت. |
مرور کلی
گزارههای حملی استاندارد ساخت
| صورت گزاره | نام و گونه | مثال |
| همه P ،S است، | A | همه وکلا آدمهای ثروتمند هستند. |
| هیچ P ،S نیست، | E | هیچ مجرم شهروند خوب نیست. |
| بعضی P ،S است، | I | بعضی مواد شیمیایی سمی هستند. |
| بعضی P ،S نیست، | O | بعضی حشرات آفت نیستند. |
تمرین
در هریک از گزارههای زیر حدهای موضوع و محمول و همچنین نام و ساخت آنها را تعیین کنید:
۱- بعضی تاریخدانان نویسندگان بسیار توانا هستند که آثار آنها مانند رمانهای ممتاز خوانده میشود.
حل:
S= تاریخدانان
P= نویسندگان بسیار توانا که آثار آنها مانند رمانهای ممتاز خوانده میشود.
ساخت(یا صورت): موجب جزئی
۲- قهرمانی که پول برای شرکت در یک مسابقۀ ورزشی پذیرفته باشد، آماتور نیست.
۳- همه ماهوارههایی که در ارتفاع کمتر از هزار مایلی قرار دارند ابزارهایی بسیار ظریف و شکننده هستند که هزاران دلار برای سازندگان آنها هزینه داشته است.
۵- برخی اعضای خانوادههای سرشناس و ثروتمند، نه ارزشمند و نه ویژگی خاص دارند.
حل:
S= اعضای خانوادههای سرشناس و ثروتمند.
P= افراد ارزشمند یا دارای ویژگی خاص.
ساخت(یا صورت): سالب جزئی
۶- بعضی نقاشیها که توسط هنرمندان چیرهدست و معروف جهانی کشیده شدهاند آثار اصیل نیستند که هیچکدامشان ارزش آن را داشته تا در موزهها نگهداری و در معرض دید عموم قرار داده شوند.
۷- همه رانندگانی که سلامت رانندگی ندارند خلافکاران خطرناک هستند که جان همراهان خود را تهدید میکنند.
۸- بعضی از سیاستمداران که نتوانستهاند به حداقل انتخاباتی دست پیدا کنند، این روزها در دولت ما به مشاغل رسمی گمارده میشوند.
۹- برخی داروها که در صورت مصرف کنترلشده بسیار مؤثر هستند؛ داروهای ضروری نیستند تا جعبه دارو در خانه از آنها پر شود.
۱۰- همه افرادی که خود، کار خلاقانه در هنر انجام نداده منتقد مسئول برای قضاوتهای ما نیستند.
حل:
S= افرادی که خود، کار خلاقانه در هنر انجام ندادهاند.
P= منتقدان مسئول برای قضاوتهای ما.
ساخت(یا صورت): سالب کلی.
