نماد و نمودار برای گزارههای حملی
گزارههای حملی (منطق قیاسی)
درآمد به منطق فصل ۶ قسمت ۸
در قسمت سه این فصل هنگام معرفی گزارههای حملی و انگاره کلاس (قسمت ۲)، نموداری کردن آنها را با نمودارهای ون دیدیم.
این قسمت به پرمایگی بیشتر این نمودارها میپردازد و افزون برآن زبان نمادین گزارههای حملی را معرفی میکند تا در قصل بعد (قیاس) بکارشان گیریم. ناگفته نماند مساله وجودی و حل آن (آمده در پاراگراف پایانی قسمت ۷ این فصل ) دانسته گرفته شده است.
۸.۶ نماد و نمودار برای گزارههای حملی
ازآنجاکه تعبیر بولی گزارههای حملی بستگی تام به انگاره کلاس خالی دارد، برای آسانی کار نماد ویژهای را برای نمایش آن— یعنی، کلاس خالی — انتخاب میکنیم. معمولاً برای این منظور نماد 0 (نماد صفر) بکار میرود. برای آنکه بگوییم کلاس مشخصشده توسط S دارای عضو نیست، بین 0 و S یک علامت مساوی قرار میدهیم. بنابراین، معادله S=0 نمایانگر آن است که sای (عضوی) در S وجود ندارد و بهعبارتدیگر این کلاس دارای عضو نیست.
گفتن آنکه کلاس مشخصشده توسط S دارای عضو است، نفی خالی بودن S است. به عبارت دیگر، گفتن آنکه S دارای عضو است همان نفی S=0 است. این نمادگذاری (نفی) را با قراردادن یک خط مورب روی علامت مساوی انجام میدهیم. بنابراین نامعادله S≠0 با نفی خالی بودن S درواقع میگوید که sای در S وجود دارد.
گزاره حملی استاندارد-ساخت همیشه به دو کلاس ارجاع دارند، بنابراین معادلهای که قرار است آنها را نشاندهد قدری پیچیدهتر خواهد بود. هرگاه دو کلاس هریک توسط یک نماد متمایز نشان داده شوند، کلاس همهچیزهایی که متعلق به هر دو هستند را میتوان با کنار هم قرار دادن دو نماد اصلی نشان داد. برای مثال، اگر S نشان دهنده کلاس طنز و P نشاندهنده کلاس شعر باشد، آنگاه کلاس همهچیزهایی که هم طنز هستند و هم شعر را با نماد SP نشان میدهیم، که نمایانگر اشعار طنزآمیز خواهد بود. به بخش مشترک دو کلاس حاصلضرب یا اشتراک دو کلاس میگویند. حاصلضرب دو کلاس عبارت است از کلاس همهچیزهای متعلق به هر دویِ آنها. کلاس همه آمریکاییها و کلاس همه آهنگسازان عبارت است از کلاس آمریکائی آهنگساز است. (باید مراقب بعضی ویژگیها در یک زبان خاص بود. برای مثال، حاصلضرب کلاس رقصنده و کلاس اسپانیولی عبارت از رقصندهای نیست که اسپانیایی باشد، بلکه رقصندهای است که اسپانیایی میرقصد.)
این روش نمادگذاری جدید راه را برای نمادگذاری گزارههای E و I بهصورت معادله و نامعادله فراهم میسازد. گزاره "هیچ P - S نیست" میگوید هیچ عضو از کلاس S عضوی از کلاس P نیست، بهعبارتدیگر، چیزی نیست که عضو هر دو کلاس باشد. این را میتوان به این صورت بازنویسی کرد که گفت، حاصلضرب دو کلاس S و P خالی است و آن را بهصورت SP=0 نمادگذاری کرد. گزاره I "بعضی P - S است" نیز میگوید حداقل یک عضو S عضو P هم است. این یعنی، حاصلضرب طبقههای S و P خالی نیست که میتوان آن را با نامعادله: SP≠0 نمادگذاری کرد.
برای نمادگذاری گزارههای A و O کافی است تا روش جدیدی را برای نمایش کلاس متمم معرفی نماییم. متمم یک کلاس عبارت از گِردآیهای از کلاس همهچیزهایی است که به کلاس اصلی تعلق نداشته باشند. همانطور که پیشتر در قسمت شش همین فصل شرح داده شد متمم کلاس سرباز عبارت است از کلاس همهچیزهایی که سرباز نیستند، یعنی غیر-سربازان. وقتی حرف S نماد کلاس همه سربازان باشد، کلاس همه غیر-سرباز را بهوسیله S̄ (که Sبار خوانده میشود) نمادگذاری میکنیم، یعنی نماد کلاس اصلی و یک علامت خط تیره بالای آن. گزاره A "همه P S است" میگوید، همه اعضای کلاس S اعضای کلاس P نیز هست؛ یا (توسط عکس متمم) "هیچ S غیر-P نیست". این مانند هر گزاره نظیر دیگر میگوید حاصلضرب طبقههای مشخصشده توسط حدهای موضوع و محمول خالی است. این گزاره با معادله 0=SP̄ نمادسازی میشود. گزاره O "بعضی P - S نیست" توسط عکس متمم به گزاره معادل I "بعضی S غیر-P است" برگردان میشود، که با نامعادله 0≠SP̄ نمادگذاری میگردد.
روابط بین چهار گزاره حملی در پیکربندی نمادگذاریشده آنها آشکار میشوند. وقتی گزارههای A و O بهصورت 0=SP̄ و 0≠SP̄ نمادگذاری شوند، آشکار است که آنها متناقضهای یکدیگر هستند. و به گونه معادل گزارههای E و I با توجه به پیکربندیهای SP=0 و SP≠0 متناقضهای یکدیگر خواهند بود. اکنون میتوان مربع تقابل بولی را، آنگونه که در شکل ۲ آمده است، نشان داد.
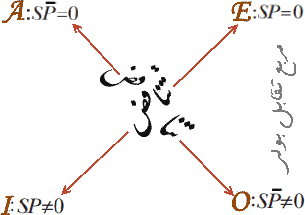
شکل ۲ - مربع تقابل بولی
هنگام توضیح چهار گونه گزاره حملی استاندارد-ساخت در قسمت سه همین فصل، روابط بین آنها را با دو دایره متقاطع و با برچسبهای S و P نشان دادیم. اکنون آن نمودار سازی برای گزارههای حملی را قدری بیشتر گسترش و نمادگذاری را توانمندتر میکنیم، بهگونهای که برای آنچه بعد خواهد آمد آسانی در تحلیل را فراهم آورد.
مرور کلی
| نمایش نمادین گزارههای حملی | |||
| صورت | گزاره | نمایش نمادی | شرح |
| A | همه P - S است | 0=SP̄ | کلاس چیزهایی که S و غیرP هستند خالی است. |
| E | هیچ P - S نیست | SP=0 | کلاس همهچیزهایی که S و P هستند خالی است. |
| I | بعضی P - S است | SP≠0 | کلاس همهچیزهایی که S و P هستند خالی نیست.(SP حداقل یک عضو دارد.) |
| O | بعضی P - S نیست | 0 ≠SP̄ | کلاس چیزهایی که S و غیر-P هستند خالی نیست. (SP̄ حداقل یک عضو دارد.) |
در ابتدا، هر کلاس را توسط یک دایره بدون علامت نشان میدهیم. سپس هر دایره را با حدی که کلاس موردنظر را مشخص میکند برچسب دار میکنیم. کلاس S توسط یک دایره ساده نمودار سازی میشود. بنابراین خواهیم داشت:

این نمودار (شکل ۳) یک کلاس است و نه یک گزاره. برای نمایان کردن آنکه S دارای عضو نیست، داخل دایره نشاندهنده آن را سایهدار میکنیم، از این طریق نشان میدهیم که دارای چیزی نیست و خالی است. برای نمایان کردن آنکه S دارای عضو است، آن را چنین تعبیر میکنیم که S حداقل دارای یک عضو هست و برای این کار جایی درون دایرهای که S را نشان میدهد یک x قرار داده و از این طریق نشان میدهیم که چیزی درون آن هست و چنین نیست که خالی باشد. بنابراین دو گزاره "sای متعلق به S نیست" و "sای متعلق به S هست"، را میتوان توسط دو نمودار مطابق شکل ۴ نشان داد.
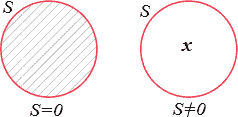
توجه داشته باشید، دایرهای که کلاس S را نموداری میکند، در عمل نمودار S̄ نیز هست، زیرا، به همان ترتیب که داخل دایره نمایانگر همه اعضای S هست، بیرون دایره نمایانگر همه اعضای S̄ خواهد بود.
برای نمودار سازی گزاره حملی استاندارد-ساخت، همانطور که پیشتر خاطرنشان کردیم، دو دایره موردنیاز است. بنابراین، کالبد یا چارچوب کار برای نمودار سازی هر گزاره حملی استاندارد-ساخت که حدهای موضوع و محمول آن به ترتیب با S و P کوتاه نویسی شدهاند، بهصورت نمودار زیر است که در آن نیز دو دایره متقاطع بکار گرفتهشدهاند (همانطور که در قسمت سه همین فصل توضیح آن آمد.)
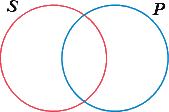
شکل ۵ نمودار دو کلاس S و P را نشان میدهد، اما در ارتباط با هیچ گزارهای نیست. این نمودار ادعایی درباره عضو داشتن یکی یا هردو یا انکار آن را نمیکند. ولی واقع مطلب آن است که در این شکل چیزی بیش از دو کلاسِ نمودارسازی شده توسط دو دایره متقاطع وجود دارد. بخشی از دایره برچسبدار S که همپوشانی با دایره برچسبدار P ندارد، همه Sهایی که P نیستند را نمودارسازی میکنند و میتوان آن را بعنوان نمایشدهنده ضرب دو کلاس S و P̄ در نظر گرفت. این بخش را میتوان با SP̄ برچسبدار کرد. ناحیه همپوشان دو دایره، ضرب دو کلاس S و P را نشان داده و نمودار همه آن چیزهایی است که به هر دو کلاس تعلق دارند. این ناحیه با SP برچسبدار شده است. آن بخش که با P برچسبدار شده و همپوشان با دایره برچسبدار S نیست نمودار همه Pهایی است که S نیستند، و ضرب کلاس S̄ و P را نشان میدهد. این بخش با S̄P برچسبدار شده است. سرانجام، آن بخش از نمودار که بیرون هر دو دایره است نمایشگر همهچیزهایی است که نه در S و نه در P هستند، و نشاندهنده کلاس چهارمی است که با S̄P̄ برچسبدار شده است.
با گذاشتن این برچسبها، شکل ۵ بهصورت شکل ۶ در زیر درخواهد آمد.
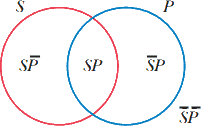
اگر در این شکل دو دایره آن، با کلاس ایرانیها (S) و کلاس شاعران(P) برچسبدار و مشخص شوند، آنگاه این نمودار را میتوان برحسب چندین کلاس مختلف تعبیر کرد. SP ضرب این دو کلاس است و شامل آن چیزهایی است که فقط و فقط به هر دویِ آنها تعلق دارد. هر عضو باید عضو هر دو، یعنی S و P باشد؛ هر عضوی باید ایرانی و شاعر باشد. این کلاس شامل همه ایرانیهای شاعر است که ازجمله و در میان بقیه شامل فردوسی و سعدی نیز است. SP̄ ضرب کلاس اول و متمم کلاس دوم است، و شامل آن چیزهایی است که متعلق به کلاس S هستند ولی متعلق به کلاس P نیستند. این ضرب کلاس ایرانیانی است که شاعر نیستند، یعنی ایرانی غیر-شاعر و دیگر فردوسی و مولوی در آن نیستند، اما در آن، ازجمله و در میان بقیه ریاضیدان جمشید کاشانی و شاه خشن آغامحمدخان قاجار هست. S̄P ضرب کلاس دوم و متمم کلاس اول است و شامل همه شاعرانی است که ایرانی نیستند. در این کلاس، غیر-ایرانی شاعر و ازجمله و در میان بقیه رابیندرانات تاگور شاعر هندی و گوته شاعر آلمانی وجود دارد. سرانجام کلاس S̄P̄ که ضرب متمم دو کلاس اصلی است. این کلاس شامل آن چیزها و فقط آن چیزهایی است که ایرانی و شاعر نیستند و درواقع این، یک کلاس بسیار وسیع هست که نهتنها شامل آدمهای انگلیسی و کوهنوردهای سوئیسی است، بلکه شامل رودخانه کارون و قله اورست هم هست. همه این کلاسها در شکل ۶ نمودارسازی شدهاند که در آن کلاس S و Pمطابق آنچه در این پاراگراف آمد تعبیر شدهاند.
نمودارهایی از این نوع موسوم به نمودارهای ون هستند و نام خود را (همانطور که پیشتر گفته شد) از جان ون منطق دان انگلیسی گرفتهاند، زیرا این روش برای نمایش طبقهها و گزارهها توسط وی ارائهشده. وقتی در این نمودارها، بخشهای مختلف برچسبدار هستند اما دارای هیچ علامتی نیستند، آنها صرفاً نشاندهنده کلاس هستند. شکل ۶ این نکته را نمایان میسازد. در این نمودارها وقتی یک دایره یا بخشی از یک دایره خالی است، این خالی بودن نشاندهنده چیزی نیست— نه میگوید عضوی از کلاس در آن ناحیه نشانداده وجود دارد و نه میگوید عضوی از کلاس در آن ناحیه نشان داده وجود ندارد.
اما با افزونههای مشخص، نمودارهای ون میتوانند علاوه بر نشاندادن کلاسها، گزارهها را نیز نمایش دهند. با سایهدار کردن برخی نواحی یا قرار دادن یک x در برخی بخشها میتوان بهطور دقیق ۴ نوع گزاره حملی استاندارد-ساخت را نمودار سازی کرد. با توجه به آنکه نمودارهای ون (همراه با نشانگذاری مناسب) گزارههای حملی را بهطور کامل و بسیار دیداری نشان میدهند، از آنها بعنوان یکی از ابزارهای بسیار توانمند و گسترده برای ارزیابی استدلالهای قیاسی استفاده میشود. اکنون نشان میدهیم که چگونه هر یک از گزارههای حملی با کاربرد این تکنیکها نشان داده میشوند.
برای نمودار سازی گزاره اره A "همه P - Sاست" که بهصورت 0=SP̄ نمادگذاری شد ناحیه SP̄ را سایهدار کرده و بهاینترتیب نشان میدهیم که در آن قسمت عضوی وجود ندارد و بهعبارتدیگر خالی است. برای گزاره E "هیچ P S نیست" که بهصورت SP=0 نمادگذاری شده، آن بخش از نمودار که نشاندهنده SP است را سایهدار کرده و بهاینترتیب نشان میدهیم که در آن قسمت عضوی وجود ندارد و بهعبارتدیگر خالی است. برای نمودار سازی گزاره I "بعضی P - Sاست" که بهصورت SP≠0 نمادگذاری شد، یک x در بخشی از نمودار که نشاندهنده کلاس SP است قرار میدهیم. این دلالت بر آن دارد که کلاس حاصلضرب خالی نیست و حداقل دارای یک عضو است؛ و سرانجام برای گزاره O "بعضی P - S نیست" که بهصورت 0≠SP̄ نمادگذاری شده یک x در بخشی که کلاس را نشان میدهد قرار داده. این x دلالت بر آن دارد که کلاس حاصلضرب خالی نیست و حداقل دارای یک عضو است. آنگونه که در شکل ۷ نشان دادهشده با کنار هم قرار دادن نمودارهایی که ۴ گزاره حملی استاندارد-ساخت را نشان میدهند، بسیار گویا و آشکار تفاوت تعبیر آنها نمایان میگردد.




اکنونکه نمودارهای «هیچ P - S نیست» و «بعضی P S نیست،» ساخته شدند و ازآنجاکه آنها همارز(معادل) با عکس مستوی خود یعنی «هیچ S P نیست» و «بعضی S P است» هستند، نمودار این گزارهها نیز هماکنون نشانداده هستند. برای نشان دادن گزاره A «همه S P است» که بهصورت 0=PS̄ نمادگذاری میشود، باید با همین چهارچوب بخشی از نمودار را که کلاس را نشان میدهد سایهدار کرد. گرچه نه بلافاصله ولی آشکار است که کلاس PS̄ و کلاس S̄P یکسان هستند. در این صورت، هر عضو متعلق به کلاس همه شاعران و کلاس همه غیر-ایرانیان باید متعلق به کلاس همه غیر-ایرانیان و کلاس همه شاعران نیز باشد. همه شاعران غیر-ایرانی همه غیر-ایرانیان شاعر هستند و برعکس آن نیز برقرار است. برای نمودار سازی گزاره O «بعضی S P نیست»، که بهصورت 0≠PS̄ نمادگذاری شده، یک x داخل بخشی از نمودار که کلاس PS̄ (مساوی با S̄P) را نشان میدهد قرار میدهیم. نمودارهای این گزارهه در شکل ۸ نشان داده شده.

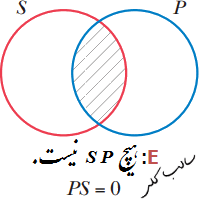


این توانمندی بیشتر نمودارهای دو دایرهای ازآنجهت اینجا گفته شد که در فصل بعدی اهمیت فراوان مییابند. در آن فصل نیاز است تا دو دایره همپوشان با برچسبهای دلخواه— به فرض S و M — بتوانند هر گزاره حملی استاندارد-ساخت شامل طبقههای S و M را بعنوان دو حد خود، بدون توجه به ترتیب رخ دادن آنها در گزاره، نمودار سازی نمایند.
نمودارهای ون نمایش شمایلگون (Iconic) گزارههای حملی استاندارد-ساخت هستند که در آنها، شمولیت و ناشمولیت مکانی متناظر با شمول و ناشمولیت غیر مکانی کلاسها است. آنها امکان یک روش نمادگذاری واضح و استثنایی را فراهم میآورند و افزون به آن، بر آنها پیسازی با سادهترین و کم واسطهترین روش آزمون اعتبار قیاسهای حملی، آنگونه که در فصل بعد خواهد آمد، میسر میگردد.
تمرین
هر یک از گزارههای زیر را بهصورت معادله یا نامعادله نشان دهید، هر کلاس را با حرف اول حد مشخصکننده آن نمایش و سپس آنها را توسط نمودارهای ون نمودارسازی کنید.
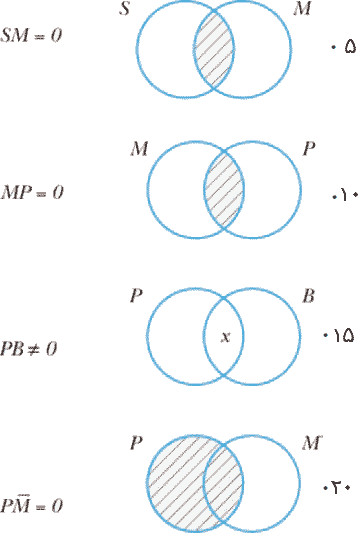
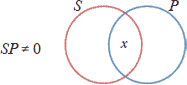
۱*- بعضی مجسمهسازان(S) نقاش(P) هستند.
۲- هیچ دستفروشی میلیونر نیست.
۳- همه بازرگانان سوداگر هستند.
۴- بعضی موسیقیدانان پیانیست نیستند.
۵*- هیچ مغازهداری عضو نیست.
۶- بعضی سیاستمداران بسیار مشهور لاابالی هستند.
۷- همه پزشکان مجاز مشغول کار در این ایالت فارغالتحصیلان مدارس پزشکی هستند که از عهده آزمونهای مخصوص تعیین کیفیت برآمدهاند.
۸- بعضی از دلالان سهام که به مشتریان خود توصیه خرید سهم میکنند خودشان سهامدار شرکتهای مورد توصیهشان نیستند.
۹- بعضی ناب گراها که هر لذت غیرمفیدی را پس میزنند بیگانه به بسیاری چیزها هستند که به زندگی ارزش زندگی کردن میدهد.
۱۰*- هیچ نقاشی مدرن شبیه عکاسی سوژه خود نیست.
۱۱- بعضی فعالان دانشجویی میانسال مردان و زنانی هستند که به دنبال بازآوردن جوانی ازدسترفته خود هستند.
۱۲- همه دانشوران قرون میانه راهبان زاهدی بودند که در صومعهها میزیستند.
۱۳- بعضی کارمندان دولت شهروند دارای روحیه اجتماعی نیستند.
۱۴- هیچ حاکم مشروط به انتخابات و عزل یک ستمگر تنبیه گر نخواهد بود.
۱۵*- بعضی بیماران که تمام نشانههای اسکیزوفرنی را نشان میدهند دچار دوقطبی روانی هستند.
۱۶- بعضی مسافران هواپیماهای بزرگ جت مسافران مشتریان راضی نشده هستند.
۱۷- بعضی کشیشان طرفدار تغییرات رادیکال اجتماعی هستند.
۱۸- بعضی مدافعان سرسخت وضع موجود عضو هیچ حزبی نیستند.
۱۹- هیچ پروژه لولهگذاری در سرزمینهای خارجی سرمایهگذاری امن نیست.
۲۰*- همه فیلمهای پورنو گرافی(P) تهدید مدنیت و نجابت(S) است.
حل تمرینهای ستاره دار: