کاهش حدهای قیاس به سه حد
قیاس در سخن
درآمد به منطق فصل ۸ قسمت ۲
درقسمت قبل، سه الگوی انحراف استدلال قیاسی از صورت استاندارد آن در زبان و سخن را دیدیم. این قسمت به الگوی انحراف دوم، یعنی حضور بیش از سه حد در استدلال قیاسی، و برگردان آن به صورت استاندارد بوسیله حذف حدهای مترادف و متمم میپردازد.
۸.۲ کاهش حدهای قیاس به سه حد
یک استدلال قیاسی باید دقیقاً سه حد داشته باشد. اگر یک استدلال در ظاهر قیاسی باشد و چنین بهنظر آید که در آن بیش از سه حد درگیرند، ممکن است بتوان آن را به یک قیاس حملی استاندارد-ساخت برگرداند، بهقسمی که حاصل همارز با آن بُوَد اما دارای سه حد و نیز کاملاً معتبر باشد. چگونه میتوان آن را انجام داد؟
■ حذف مترادفها
یک طریق، حذف مترادفها است. مترادف یک حد در قیاس یک حد چهارم نیست و درواقع روشی دیگر برای رجوع به یکی از سه حد درگیر است. بنابراین، ما کار را با حذف مترادفها در صورت وجود آغاز میکنیم. برای مثال، به نظر میرسد قیاس زیر دارای شش حد باشد.
هیچ ثروتمندی بیخانمان نیست.
همه طبیبها پولدار هستند.
ــــــــــــــــ
بنابراین، هیچ پزشکی آسمانجل نیست.
ولی "ثروتمند" و "پولدار" مترادف هستند و همینطور است "طبیب" و "پزشک" و سرانجام "بیخانمان" و "آسمانجل" هم مترادفاند. وقتی این مترادفها حذف شوند استدلال بهصورت زیر برگردان میشود.
هیچ ثروتمندی بیخانمان نیست.
همه پزشکها ثروتمند هستند.
ــــــــــــــــ
بنابراین، هیچ پزشکی بیخانمان نیست.
این استدلال بهصورت استانداردِ EAE-۱ (سلرنت-Celarent) است و بهآسانی میتوان دید که معتبر است.
■ حذف کلاسهای متمم
راه دوم برای کاهش حدها به سه حد میتواند حذف کلاسهای متمم باشد. برای مثال به استدلال زیر که همه گزارههای آن حملی و بهصورت استاندارد نیز هستند توجه نمایید:
همه پستانداران حیوان خونگرم هستند.
هیچ سوسمار حیوان خونگرم نیست.
ــــــــــــــــ
بنابراین همه سوسمارها غیر پستاندار هستند.
در سطح به نظر میرسد که این استدلال معتبر نباشد، زیرا دارای چهار حد است— و نیز در آن، یک نتیجه ایجابی از مقدمه سلبی استخراج شده است که این شکستن یکی از قواعد قیاس است.
ولی، اگر این استدلال را به یک قیاس حملی به صورت استاندارد [دارای سه حد] برگرداند، آنگاه کاملاً معتبر خواهد بود. میتوانیم تعداد حدها را به سه کاهش دهیم، زیرا دو حد آن («پستانداران» و «غیرپستانداران») متمم یکدیگرند. بنابراین، بهوسیله برگردان عکس متمم نتیجه (برای بدست آوردن عکس متمم یک گزاره کیفیت آن را تغییر داده و حد محمول را با متمم آن تعویض میکنیم) خواهیم داشت «هیچ سوسمار پستاندار نیست.» با کار زدن این استنتاج بیواسطه معتبر به برگردانِ صورت استانداردِ استدلال اصلی خواهیم رسید:
همه پستانداران حیوانات خونگرم هستند.
هیچ سوسماری حیوان خونگرم نیست.
ــــــــــــــــ
بنابراین، هیچ سوسماری پستاندار نیست.
این قیاس اخیر منطقاً همارز با قیاس اصلی است، زیرا دارای مقدمات یکسان و نتیجه منطقاً همارز است. صورت این قیاس AEE-۲ (کامسترس-Camestrs) است.
ممکن است بیش از یک برگردان به ساخت-استاندارد برای یک استدلال قیاسی وجود داشته باشد، اما اگر یکی از برگردانها به یک قیاس معتبر منجر گردد بقیه نیز میباید معتبر باشند. لذا، برای مثال، استدلال قبلی میتواند به طریق دیگر (اما منطقاً همارز) به صورت استاندارد کاهش داده شود. این بار نتیجه را دستنخورده باقی میگذاریم و با مقدمات کارخواهیم کرد. عکس نقیض مقدمه اول را به دست میآوریم و مقدمه دوم را به عکس متمم برگردان میکنیم. در این صورت خواهیم داشت:
همه غیر(حیوانات خونگرم) غیر پستاندار هستند.
همه سوسمارها غیر(حیوانات خونگرم) هستند.
ــــــــــــــــ
بنابراین همه سوسمارها غیر پستاندار هستند.
این نیز یک برگردان معتبر بهصورت AAA-۱ (باربارا) است که با همه قواعد قیاس همنوایی دارد.
هرگاه در یک استدلال قیاسی چهار حدی، یکی از حدود متمم یکی دیگر از حدود باشد، آنگاه این استدلال قیاسی، قابل برگردان به یک قیاس حملی استاندارد-ساخت و منطقاً همارز با استدلال اصلی است. و همینطور اگر یک استدلال قیاسی دارای پنج حد باشد، قابل کاهش بهصورت استاندارد خواهد بود، هرگاه دو حد آن متمم دو حد دیگر باشد. و حتی اگر یک استدلال قیاسی دارای شش حد باشد، قابل کاهش بهصورت استاندارد خواهد بود، هرگاه سه حد آن متمم سه حد دیگر باشد. کلید تمام این فرو کاهیدنها کار زدن استنتاجهای بیواسطه معتبر: عکس مستوی، عکس متمم و عکس نقیض است.
ممکن است به بیش از یک استنتاج بیواسطه برای کاهش استدلال به ساخت استاندارد نیاز باشد. به استدلال زیر توجه نمایید:
هیچ غیر مقیم شهروند نیست.
همه غیر شهروندان غیر رأیدهنده هستند.
ــــــــــــــــ
بنابراین همه رأیدهندگان مقیم هستند.
این استدلال شش حد دارد اما معتبر است. این را با کاهش به صورت استاندارد با بیش از یک روش میتوان نشان داد. یک روش که شاید طبیعیترین و آسانترین نیز باشد برگردان به عکس مستوی و سپس عکس متمم مقدمه اول باشد. این، «همه شهروندان مقیم هستند.» را به دست میدهد. سپس عکس نقیض مقدمه دوم است که «همه رأیدهندگان شهروند هستند» را به دست میدهد. سرانجام استدلال به ساخت استاندارد بهقرار زیر خواهد بود:
همه شهروندان مقیم هستند.
همه رأیدهندگان شهروند هستند.
ــــــــــــــــ
بنابراین همه رأیدهندگان مقیم هستند.
حد وسط «شهروند» حد موضوع مقدمه مِهین و حد محمول مقدمه کِهین است، بنابراین در شکل اول است. این قیاس AAA-۱ (باربارا) است که آشکارا معتبر است.
تمرین
استدلالهای قیاسی زیر را بهصورت استاندارد برگردانده و سپس اعتبار آنها را با استفاده از نمودار ون یا با کاربرد قواعد قیاس بیازمایید.
۱- بعضی سخنوران افرادی با نیروی تمامنشدنی هستند. هیچ سخنوری تحصیلنکرده نیست. بنابراین، بعضی تحصیلکردهها افرادی با نیروی تمامنشدنی هستند.
حل:
این استدلال را میتوان بهصورت زیر برگردان کرد:
بعضی سخنوران افرادی با نیروی تمامنشدنی هستند. (بعضی س ن است.).
همه سخنوران تحصیلکرده هستند. (بهوسیله عکس متمم: همه س ت است.).
بنابراین بعضی تحصیلکردگان افرادی با نیروی تمامنشدنی هستند. ( بعضی ت ن است.)
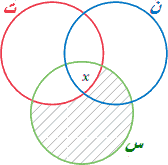
همانطور که در نمودار ون نشانداده شده این قیاس معتبر است.
۲- بعضی فلزات کمیاب و مواد گران هستند، اما هیچیک از مواد جوشکاری غیرفلز نیست، بنابراین بعضی مواد جوشکاری کمیاب و مواد گرانی هستند.
۳- بعضی از ملل آسیائی غیر متخاصم بودند، و از آنجائی که همه متخاصمین متحد آلمان یا بریتانیا بودند، بعضی ملل آسیا متحد آلمان یا بریتانیا نبودند.
۴- بعضی غیر مشروبنوشها قهرمان هستند، چون هیچ مشروبنوش در شرایط جسمی خوب نیست، و بعضی در شرایط فیزیکی خوب غیر قهرمان هستند.
۵- همهچیزهای شعلهور شدنی چیزهای غیرایمن هستند. بنابراین همه چیزهای ایمن غیرقابلانفجار هستند، زیرا همه قابل انفجارها شعلهور شدنی هم هستند.
وقتی: ج = قابلانفجار ش = چیزهای شعلهور شدنی ی = چیزهای ایمن
قیاس به ساخت استاندارد زیر برگردان میشود:
همه ج ش است.
هیچ ش ی است.
بنابراین هیچ ی ج است.
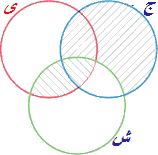
که با توجه به نمایش آن در نمودار ون این قیاس (در کامنس) معتبر است.
۶- همهچیزهای خوب این دنیا قابلمعاوضه هستند ، هیچچیز خوب این دنیا غیرمادی نیست، و هیچچیز مادی غیرقابلمعاوضه نیست.
۷- همه آنهایی که عضو نیستند یا مهمان یک عضو نیستند حذفشدهاند. بنابراین هیچ غیر محلی عضو یا مهمان یک عضو نیست، زیرا همه آنهایی که شامل شدهاند محلی هستند.
۸- همهچیزهای فانی ناقص هستند، و هیچ بشری غیر فانی نیست. بنابراین همه موجودات کامل غیر بشری هستند.
۹- همهچیزهای حاضر غیر آزاردهنده هستند، بنابراین هیچ آزاردهندهای شئ قابلدیدن نیست. زیرا همه اشیاء دیدنی چیزهای غایب هستند.
۱۰- هیچچیز مفید چیزهایی بیشتر از شش فوت طول نیستند، زیرا همه چیزهایی که برای انبار شدن سخت هستند چیزهای بیهوده هستند و هیچ شئ بیشتر از شش فوت طول برای انبار شدن آسان نیست.
وقتی: ب = چیزهای بیشتر از شش فوت طول س = چیزهای سختانبار شدنی م = چیزهای مفید
قیاس به ساخت استاندارد زیر برگردان میشود::
همه ب س است.
هیچ س م است.
بنابراین هیچ م ب است.
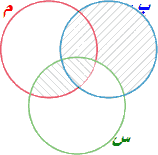
که با توجه به نمایش آن در نمودار ون این قیاس (در کامنس) معتبر است.
