زنجیره‌های منطقی (تسلسل منطقی)

مواقعی هست که تنها یک قیاس حملی برای استخراج نتیجه موردنظر از مقدمات کفایت نمی‌کند، برای نمونه از مقدمات:

همه سیاستمداران مبادی‌آداب هستند.
بعضی اعضای دولت سیاستمدار هستند.
همه اعضای دولت افراد دارای زندگی عادی هستند.

نمی‌توان نتیجه:

بعضی افراد دارای زندگی عادی مبادی‌آداب هستند.

 را فقط با یک قیاس حملی استخراج کرد. حال‌آنکه مقدمات دربردارنده نتیجه گفته‌شده هستند. برای استخراج این نتیجه بجای یک قیاس نیازمند به دو قیاس هستیم . باید به یک فرایند گام‌به‌گام استدلالی روی آورد که در آن، هر گام خود یک قیاس حملی مجزا باشد. اگر استدلال بالا را به‌صراحت بازگو کنیم، استدلال موردنظر به‌قرار زیر خواهد شد.

همه سیاستمداران مبادی‌آداب هستند.
بعضی اعضای دولت سیاستمدار هستند.
_______
بنابراین بعضی اعضای دولت مبادی‌آداب هستند.
همه اعضای دولت افراد دارای زندگی عادی هستند.
_______
بنابراین بعضی افراد دارای زندگی عادی مبادی‌آداب هستند.

هرگاه استدلالی مانند این، نهفنه‌ ارائه گردد، به قسمی که فقط مقدمات و نتیجه پایانی بیان شوند به آن زنجیره منطقی (یا تسلسل منطقی) گفته می‌شود➥.  یک زنجیره منطقی ممکن است، سه، چهار، یا هر تعداد مقدمات داشته باشد و درواقع بعضی از آن‌ها نیز بسیار طولانی هستند. مثال زیر از آثار فیلسوف گاتفرید لاییپ‌نیتش "مناد شناسی/Monadology" برگرفته‌شده است:

روح بشر چیزی است که فعالیت آن اندیشیدن است. چیزی که فعالیت آن اندیشیدن است، فعالیت آن بی‌واسطه و بدون بازنمایی اجزای آن درک می‌گردد. چیزی که فعالیت آن بدون بازنمایی اجزای آن و بدون واسطه درک می‌شود، چیزی است که فعالیت آن دارای اجزاء نیست. چیزی که فعالیت آن دارای اجزا نیست، چیزی است که فعالیت آن حرکت نیست و چیزی که فعالیت آن حرکت نیست یک جسم نیست. چیزی که جسم نیست در فضا نیست. چیزی که در فضا نیست مستعد حرکت نیست. چیزی که مستعد حرکت نیست ماندگار است (زیر ناماندگاری حرکت اجزاء است). چیزی که ناماندگار است فسادپذیر نیست. چیزی که فسادپذیر نیست فناناپذیر است. بنابراین روح بشر فناناپذیر است.

این زنجیره منطقی ده مقدمه دارد! هر زنجیره منطقی را می‌توان با صراحت دادن به مقدمات یا میان نتیجه‌ها و سپس با بررسی هر قیاس به‌دست‌آمده به‌طور جداگانه مورد آزمون قرار داد. اگر در زنجیره استدلال بالا از چندمعنایی گزاره‌ها که ممکن است وجود داشته باشد صرف‌نظر کرده، آنگاه اعتبار استدلال زنجیره‌ای لایب نیتس به‌سادگی قابل‌بررسی خواهد بود.

در اینجا مفید است تا در رابطه با تمرین‌های آمده در آخر این فصل خاطر نشان کرد که، یک زنجیره منطقی استاندارد-ساخت (یا تسلسل منطقی استاندارد-ساخت) است وقتی همه گزاره‌های آن استاندارد-ساخت باشند و هر حد دقیقاً دو بار روی‌داده، و نیز هر گزاره (به‌جز گزاره آخر) دارای یک حد مشترک با گزاره بلافاصله بعد از خود باشد. بنابراین برگردان ساخت استاندارد زنجیره استدلال ارائه‌شده توسط لوئیس کارول (ریاضیدان و منطق دان انگلیسی و به‌طور عمده مشهور به خاطر داستان "آلیس در سرزمین عجایب") که به شرح زیر آمده است:

(۱) هرکس که دارای عقل سلیم است می‌تواند منطقی عمل کند.
(۲) هیچ دیوانه‌ای برای عضویت در هیئت‌منصفه شایسته نیست.
(۳) هیچ‌یک از پسران تو نمی‌توانند منطقی رفتار کنند.
________
بنابراین هیچ‌کدام از پسران تو شایسته عضویت در هیئت‌منصفه نیست،

به‌قرار زیر است:

(‘۲) همه افراد شایسته عضویت در هیئت‌منصفه افرادی دارای عقل سلیم هستند.
(‘۱) همه افراد دارای عقل سلیم افراد با توان عمل منطقی هستند.
(‘۳) هیچ‌یک از پسران تو افراد با توان عمل منطقی نیستند.
________
بنابراین هیچ‌یک از پسران شما افراد شایسته عضویت در هیئت‌منصفه نیستند.

می‌توان میان-نتیجه از بین رفته را به‌صراحت بیان کرد و سپس قیاس‌های حملی حاصل را (مطابق آنچه در فصل هفت قسمت ۳ یا فصل هفت قسمت ۴ آمده) آزمون کرد.

تمرین

آ زنجیره استدلال‌های زیر را به ساخت استاندارد برگردانده و سپس اعتبار آن‌ها را بررسی نمایید➥.

[۴]- همه تمرینات زیر به‌جز ۴ و ۶ قسمت (آ)، بدون تصرف از کتاب منطق نمادین تألیف لوئیس کارول انتخاب‌شده‌اند.

Lewis Carroll’s Symbolic Logic (New York: C. N. Potter, 1977)

۱.

(۱) اطفال غیرمنطقی هستند.
(۲) هیچ‌کس بی‌مهارت نیست وقتی بتواند تمساح‌ها را اداره کند.
(۳) افراد غیرمنطقی بی‌مهارت هستند.
____________
بنابراین اطفال نمی‌توانند تمساح‌ها را اداره کنند.

حل:
برگردان به ساخت استاندارد:

(‘۱) همه اطفال افراد غیرمنطقی هستند.
(‘۲) همه افراد غیرمنطقی بدون مهارت هستند.
(‘۳) هیچ شخصی که بتواند تمساح‌ها را اداره کند شخص بدون مهارت نیست.
____________
بنابراین هیچ طفل فردی نیست که بتواند تمساح را اداره کند.

آن‌گونه که در زیر آمده، این زنجیره منطقی شامل دو قیاس است،

همه I  B است.
همه D  I است.
بنابراین همه D  B است.

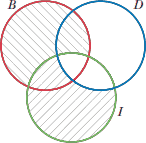
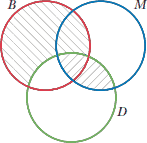
همه D  B است.
هیچ D  M نیست.
بنابراین هیچ B  M نیست.

۲.
(۱) هیچ فرد آزموده بدون مهارت نیست.
(۲) جنکین همیشه ناآزمودگی از خود نشان می‌دهد.
(۳) هیچ فرد ماهر همیشه خام‌دستی نمی‌کند.
____________
بنابراین جنکین ناآزموده است.

۳.
(۱) تنها کتاب‌هایی را که من در این کتابخانه برای خواندن توصیه نمی‌کنم کتاب‌های ناسالم هستند.
(۲) کتاب‌های سری شده خوب نگارش شده‌اند.
(۳) همه کتاب‌های رمان دارای فضای داستانی سالم هستند
(۴) من توصیه نمی‌کنم که تو هیچ‌یک از کتاب‌های سری‌نشده را بخوانی.
____________
بنابراین همه کتاب‌های رمان در این کتابخانه خوب نگارش شده‌اند.

۴.
(۱) فقط تحصیل‌کردگان با محتوی می‌توانند استاد آکسفورد شوند.
(۲) هیچ روح غیر حساس دوستدار عمیق موسیقی نیست.
(۳) هیچ‌کسی که روح حساس ندارد نمی‌تواند عاشق‌پیشه باشد.
(۴) تحصیل‌کرده با محتوایی وجود ندارد که دوستداران عمیق موسیقی نباشد.
____________
بنابراین همه استادان آکسفورد عاشق‌پیشه هستند.

۵.
(۱) هیچ شعر دلپذیری نزد اهل ذوق نامحبوب نیست.
(۲) هیچ شعر مدرن خالی از اقتباس نیست.
(۳) همه اشعار شما درباره حباب صابون هستند
(۴) هیچ شعر اقتباسی نزد اهل ذوق محبوب نیست.
(۵) فقط یک شعر مدرن می‌تواند درباره حباب صابون باشد.
____________
بنابراین همه اشعار شما غیر دلپذیر هستند.

حل:

(‘۱) همه اشعار دلپذیر شعرهایی که نزد اهل ذوق محبوب‌اند  هستند.
(‘۴) هیچ شعر تأثیر پذیرفته شعرهایی که نزد اهل ذوق محبوب‌اند نیست.
(‘۲) همه شعر‌های مدرن شعر تأثیر پذیرفته است.
(‘۵)همه شعر‌های که موضوع آن‌ها حباب صابون است شعر مدرن است.
(‘۳)همه شعر‌های شما شعرهایی که موضوع آن حباب صابون است هستند .
____________
بنابراین هیچ شعر شما دلپذیر نیست.

 

همه P  I است.
هیچ P  A نیست.
بنابراین هیچ I  A نیست.

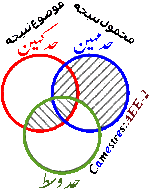
هیچ I  A نیست.
همه A  M است.
بنابراین هیچ I  M نیست.

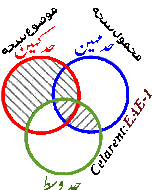
هیچ I  M نیست.
همه M  S است.
بنابراین هیچ I  S نیست.

هیچ I  S نیست.
همه S  Y است.
بنابراین هیچ I  Y نیست.

۶.
(۱) هیچ‌کس جز نویسندگان شاعر نیست.
(۲) فقط افسران نظامی فضانورد هستند.
(۳) هرکس که به یک مجله جدید کمک کند شاعر است.
(۴) هیچ‌کس نویسنده و هم افسر نظامی نیست.
____________
بنابراین یک فضانورد به یک مجله جدید کمک نمی‌کند.

---

---

---

---

  ب هریک از مجموعه گزاره‌های زیر می‌توانند به‌عنوان مقدمات برای یک زنجیره منطقی معتبر بکار روند. برای هر مجموعه نتیجه را تعیین و ثابت کنید که استدلال معتبر است.

۱.
(۱) هیچ فردی روزنامه تایمز نمی‌خواند مگر تحصیل‌کرده باشد.
(۲) هیچ خارپشتی نمی‌تواند بخواند.
(۳) آن‌هایی که نمی‌توانند بخوانند تحصیل‌کرده نیستند.

حل:

(‘۱) همه آن‌هایی که روزنامه تایمز می‌خوانند تحصیل‌کرده هستند.
(‘۳) هیچ موجودی که نمی‌تواند بخواند تحصیل‌کرده نیست.
(‘۲) همه خارپشت‌ها موجوداتی که نمی‌توانند بخوانند هستند.
بنابراین هیچ خارپشت آن‌هایی که روزنامه تایمز می‌خوانند نیست.

 

همه W  T است.
هیچ W  C نیست.
بنابراین هیچ T  C نیست.

هیچ T  C نیست.
همه C  H است.
بنابراین هیچ T  Hنیست.

۲.
(۱) همه پودینگ‌ها لذیذ هستند.
(۲) این غذا پودینگ است.
(۳) هیچ‌چیز لذیذی بی‌خطر نیست.

۳.
(۱) تنها غذاهایی را دکتر برای من تجویز کرده که خیلی مغذی نیستند.
(۲) هیچ‌چیزی که باب دل من باشد برای غذای شب مناسب نیست.
(۳) کیک‌های عروسی همیشه مغذی هستند.
(۴) دکتر همه غذاهای شب را برای من تجویز کرده است.

۴.
(۱) همه دختران من لاغر هستند.
(۲) هیچ‌کدام از فرزندان من که ورزش نمی‌کنند سلامت نیستند.
(۳) همه پرخورهایی که فرزند من هستند چاق هستند.
(۴) هیچ پسر من ورزش نمی‌کند.

۵.
(۱) وقتی من بدون غرولند مشغول کار با مثال‌های منطق هستم، تو مطمئن باش موردی است که می‌توانم آن‌ها بفهمم.
(۲) این زنجیره منطقی مطابق مثال‌هایی که من با آن‌ها آشنا هستم مرتب‌نشده است.
(۳) هیچ مثال ساده‌ای تابه‌حال سرم را به درد نیاورده.
(۴) من نمی‌توانم مثال‌هایی را بفهمم که مطابق مثال‌هایی که با آن‌ها آشنا هستم مرتب‌نشده باشد.
(۵) من هرگز برای مثالی غرولند نمی‌کنم، مگر سرم را درد آورده باشد.

حل:

(‘۲) این زنجیره‌های منطقی مثال‌هایی مثل آنچه من عادت دارم به‌قاعده مرتب‌نشده است.
(‘۴) هیچ مثالی مثل آنچه من عادت دارم به‌قاعده مرتب نشده مثال‌هایی که من بفهمم  نیستند.
(‘۱) همه مثال‌هایی که من برایشان غرولند نمی‌کنم مثال‌هایی که می‌توانم بفهمم هستند.
(‘۵) همه مثال‌هایی که سر من را به درد نمی‌آورند  مثال‌هایی که من غرولند نمی‌کنم هستند.
(‘۳) همه مثال‌های آسان مثال‌هایی هستند که سر مرا به درد نمی‌آورند.
بنابراین، این زنجیره‌های منطقی مثال‌های آسان نیستند.

هیچ U  N نیست.
همه N  S است.
بنابراین هیچ U  S نیست.

همه U  G است.
هیچ U  S نیست.
بنابراین هیچ G  S نیست.

همه G  H است.
هیچ G  S نیست.
بنابراین هیچ H  S نیست.

همه H  E است.
هیچ H  S نیست.
بنابراین هیچ E  S نیست.