سور عمومی و سور وجودی
منطق محمولات
درآمد به منطق فصل ۱۱ قسمت ۳
قسمت پیشین به نمادگذاری ثابتهای انفرادی، متغیرهای انفرادی و توابع گزارهای (حروف محمولی) در روند گسترش زبان نمادین بسوی زبان محمولات پرداخت. این قسمت به نماد سازی سور عمومی، سور وجودی، روابط آنها نیزنمایاندن این روابط در مربع تقابل مدرن میپردازد.
۳.۱۱ سور عمومی و سور وجودی
سور عمومی
Universal quantifier
نماد (x) قبل از تابع گزارهای بکار میرود تا بگوید محمول بدنبال آمده برای هر چیزی درست است.
تعمیم
Generali-zation
روند تشکیل گزاره از یک تابع گزارهای با گذاشتن یک سور عمومی یا یک سور وجودی قبل ار آن.
سور وجودی
Existen-tial quantifier
نماد (x∃) که دلالت برآن دارد، تابع گزارهای درپی آمده دارای حداقل یک مورد جانشینی درست است.
یک گزاره شخصی تایید میکند، شئای انفرادی دارای محمول [تابع گزارهای] داده شدهای (معین) است، بنابراین این گزاره شخصی مورد جانشینی یک تابع گزارهای است. اگر محمول M برای فانی و B برای زیبا باشد، آنگاه محمولهای ساده Mx و Bx را داریم که البته مدعی فانیبودن یا زیبایی هیچ شئ خاصی نیستند. اگر سقراط را جانشین متغیر انفرادی x کنیم، گزارههای شخصی "سقراط فانی است" و "سقراط زیبا است" را بدست میآوریم. ممکن است بخواهیم بگوئیم بیش از یک شئ ویژگی مورد نظر را دارد. و نیز بخواهیم بگوئیم "هر چیز فانی است" یا "بعضی چیزها زیبایند." این عبارات شامل حد محمول هستند ولی گزاره شخصی نیستند، زیرا آنها بطور خاص به شئ انفرادی خاصی اشاره نمیکنند. اینها گزاره عام هستند.
اکنون به اولین گزاره، یعنی «هر چیز فانی است»، از دو گزاره عام بالا نزدیکتر نگاه میکنیم، این گزاره را میتوان به روشهای مختلف بیان کرد که منطقاً همارز باشند. میتوان بجای آن گفت "همه چیزها فانی هستند" یا میتوان آنرا به این شیوه گفت که:
هرچه باشد شئ انفرادی دادهشدهای، آن فانی است.
در این پیکربندی اخیر کلمه "آن" یک ضمیر اشاره است که ارجاع به واژه "شئ" که مقدم به آن آمده دارد. میتوان بجای ضمیر اشاره و همچنین مقدم آن حرف x، یعنی همان متغیر انفرادی، را بکاربریم. بنابراین، اولین گزاره عام را میتوان بصورت زیر بازنویسی کرد:
برای هر x داده شده، x فانی است.
یا آن نمادسازی را که در قسمت قبل معرفی کردیم بکاربرده و بنویسیم:
برای x داده شده Mx.
میدانیم Mx یک تابع گزارهای است و نه یک گزاره. اما در این پیکربندی آخری یک عبارت داریم که شامل Mx است و آشکارا گزاره است. رسم چنین است که «برای x داده شده» را با (x) نمادسازی کرده و آنرا سور عمومی نامید. اکنون می توان گزاره عام اولی را بهتمامی بصورت
(x)Mx
نمادین کرد که روشن میگوید "هر چیز فانی است."
این تحلیل نشان میدهد میتوان یک تابع گزارهای را نه تنها با جانشینی، بلکه با تعمیم یا سوردار کردن نیز به گزاره تبدیل کرد.
حال به گزاره عام دوم که وارد میدان کردهایم نگاه میکنیم: "بعضی چیزها زیبایند." این را نیز میتوان بصورت زیر بازگفت:
"حداقل یک چیز وجود دارد که زیباست"
در این پیکربندی اخیر کلمه "که" یک ضمیر موصولی است که برگشت ارجاع به "شئ" دارد. با بکاربردن متغیر انفرادی x بجای ضمیر "که" و همینطور مقدم آن "شئ"، میتوان دومین گزاره عام را بصورت زیر بازنویسی کرد
حداقل یک x وجود دارد، بقسمی که x زیباست.
یا با کارزدن نمادسازی برای محمولات میتوان نوشت:
حداقل یک x وجود دارد، بقسمی که Bx.
بار دیگر مشاهده میکنیم که گرچه Bx یک تابع گزارهای و نه گزاره است ولی اینجا یک عبارت داریم که شامل Bx است و گزاره هم است. رسم چنین است که عبارت «حداقل یک x وجود دارد بقسمی که» را با "x∃" نمادسازی کرده و آنرا سور وجودی نامید. بنابراین، دومین گزاره عام را میتوان بهتمامی مطابق
(∃x)Bx
نمادسازی کرد که دقیقاً میگوید «بعضی چیزها زیبایند.»
بنابراین از آنچه تا اینجا گفته شد، میتوان از توابع گزارهای با تخصیص (مورد گذاری)، یعنی با جانشینی یک ثابت انفرادی بجای متغیر انفرادی آن، یا با تعمیم، یعنی قراردادن یک سور عمومی یا وجودی قبل از آن، گزارهها را ساخت. نیز در نظر داشته باشید که:
سور عمومی تابع گزارهای، x)Mx)، درست است، اگر و فقط اگر همه موردهای جانشینی آن درست باشند؛ این چیزی است که اینجا از عام بودن مراد نظر است. همچنین سور وجودی تابع گزارهای (∃x)Bx درست است اگر و فقط اگر حداقل یک مورد جانشینی درست داشته باشد.
برای فهم گزارههای سوردار و اینکه چگونه به هم ربط دارند نشان میدهیم که چگونه میتوان مربع تقابل سنتی را بر حسب گزارههای سوردار بازنمایان کرد. برای اینکار در بقیه این قسمت فرض کنیم (که کسی هم نمیخواهد آنرا انکار کند) حداقل یک شئ انفرادی وجود دارد. تحت این فرض خیلی ضعیف، هر تابع گزارهای دارای یک مورد جانشینی است، موردی که ممکن است درست یا نادرست باشد. اما بطور مطمئن، تحت این فرض، اگر سور عمومی یک تابع گزارهای درست باشد آنگاه سور وجودی آن نیز باید درست باشد. بعبارت دیگر، اگر هرM - x است، آنگاه یک شئ است که آن شئ M است.
تا اینجا گزارههای موجب شخصی بعنوان مورد جانشین توابع گزارهای ارائه شدهاند. Mx (هرM - x است) یک تابع گزارهای است. Ms که میگوید "سقراط فانی است" یک مورد آن است، یعنی یک گزاره موجب شخصی است. اما همه گزارهها ایجابی نیستند. ممکن است کسی منکر آن شود که "سقراط فانی است" و بگوید Ms~، یعنی "سقراط فانی نیست." اگر Ms مورد جانشینی Mx است، آنگاه Ms~ میتواند مورد جانشین Mx~ درنظر گرفتهشود. و بنابراین میتوانیم درک مفهومی خود از توابع گزارهای را گسترش دهیم، گسترشی فراتر از محمولات ساده که در قسمت قبل معرفی شدند و اجازه دهیم آنها شامل نماد نقیض "~" نیز باشند.
با دسترسی به نماد نقیض، میتوانیم درک خود از سورگذاری را مطابق آنچه میآید ژرفا دهیم. کار را با گزاره
هیچ چیز کامل نیست.
که میتوان آنرا بصورت زیر بازنویسی کرد آغاز میکنیم:
هر چیز غیر کامل است.
که به نوبت خود میتوان آنرا بهصورت زیر بازنویسی کرد :
برای هر شئ انفرادی مفروض هرچه که میخواهد باشد، آن شئ کامل نیست.
که این نیز میتواند بصورت زیر بازنویسی شود:
برای هر x مفروض (دادهشده)، x کامل نیست.
اگر P ویژگی کاملبودن را نمادین کند، آنگاه میتوان نمادگذاری را که هماکنون گسترش دادیم (سور و نماد نقیض) را بکار ببریم تا این گزاره ("هیچ چیز کامل نیست") را بصورت
(x)~Px
بیان کنیم.
☚: اکنون میتوان بعضی روابط مهم بین سور وجودی و عمومی را فهرست و نمایش دهیم.
یکم: گزاره عام (کلی) «هر چیزی فانی است» توسط گزاره عام (وجودی) «بعضی چیزها فانی نیستند» نفی میشود. ازآنجاکه هریک ار اینها نفی دیگریست، میتوان با اطمینان گفت (با قراردادن نماد نقیض در اول یکی) که دو شرطی
~(x)Mx 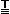 (∃x)~Mx
(∃x)~Mx
به ضرورت، منطقاً-درست (موردی از صورت توتولوژیک) است.
دوم: «هر چیزی فانی است» دقیقاً همانچیزی را میگوید که توسط «چیزی نیست که فانی نباشد» گفته میشود ــ که میتوان آنرا به دوشرطی دیگری و منطقاً-درست پیکربندی کرد:
(x)Mx 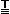 ~(∃x)~Mx.
~(∃x)~Mx.
سوم:، آشکار است که گزاره عام (کلی) «هیچ چیز فانی نیست» توسط گزاره «بعضی چیزها فانی هستند» نفی میشود. بهشیوه نمادین میتوان گفت
نفی میشود (∃x)Mx توسط (x)~Mx
و از آنجا که هر یک نفی دیگر است با اطمینان (مجدداً با مقدم کردن یکی با یک نماد نقیض) دو شرطی:
~(x)~Mx 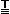 (∃x)Mx
(∃x)Mx
به ضرورت، منطقاً-درست است.
و سرانجام، چهارم: «هر چیزی فانی نیست» دقیقاً آن چیزی را میگوید که توسط «چیزی نیست که فانی باشد» گفته میشود – که میتوان آنرا با دوشرطی زیر پیکربندی کرد:
(x)~Mx  ~(∃x)Mx
~(∃x)Mx
این چهار دو شرطی منطقاً-درست روابط بین سورهای عمومی و وجودی را بیان میکنند. هرگزارهای که در آن سور با نماد نقیض مقدم شده باشد را میتوان با گزارهای که همارز با آن است تعویض کرد، بقسمیکه در آن سور با نماد نقیض مقدم نشده باشد (با کارزدن دو شرطیهای منطقاً معتبر که در بالا گفته شد.) این دو شرطیها را در زیر فهرست و محمول مثالی M (برای فانیبودن) را با نماد Φ (حرف یونانی باصدای فی) که دلالت بر هر محمولی، هرچه که میخواهد باشد دارد، تعویض میکنیم.
همارزی های منطقی ــ بیانگر روابط بین سورهای وجودی و عمومی
[(x)Φx]  [~(∃x)~Φx]
[~(∃x)~Φx]
[(∃x)Φx]  [~(x)~Φx]
[~(x)~Φx]
[(x)~Φx]  [~(∃x)Φx]
[~(∃x)Φx]
[(∃x)~Φx]  [~(x)Φx]
[~(x)Φx]
روابط بین سور عمومی و وجودی را میتوان با جنبه نموداری بیشتر با یک مربع آراسته آنچنان که در شکل ۱.۱۱ آمده است، نشانداد.
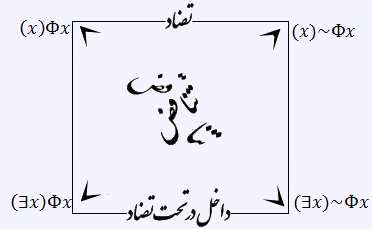
با نگهداشتن فرض وجود حداقل یک شئ انفرادی و با رجوع به این مربع میتوان گفت:

۱- دو گزاره در سطر بالایی متضاد (Contraries) هستند، یعنی هر دو میتوانند نادرست باشند ولی هر دو نمیتوانند درست باشند.
۲- دو گزاره در سطر پائینی داخل در تحت تضاد (Subcontraries) هستند، یعنی هر دو میتوانند درست باشند ولی هر دو نمیتوانند نادرست باشند.
۳- گزارههای واقع در دو سر هر قطر متناقض (Contradictories) هستند، که یکی باید درست و دیگری نادرست باشد.
۴- در هر دو ساق مربع، گزاره پائینتر لازم شده (مستلزَم) توسط گزاره بلافاصله بالای آن است.
■ ■ ■ ■ ■
در زیر است.
استدلال
