اثبات اعتبار در نظربه سورها
منطق محمولات
درآمد به منطق فصل ۱۱ قسمت ۵
قسمت پیشین به تحلیل گزاره حملی (قضیههای حملی در منطق قدیم) و روابط بین آنها در پرتو منطق جدید پرداخت. این قسمت، در ادامه تکمیل قواعد استنتاج، ۴ قاعده را به قرار: ۱- تخصیص کلی ۲- تعميم کلی ۳- تخصيص وجودی و ۴- تعمیم وجودی برای اثبات اعتبار استدلال در منطق محمولات معرفی میکند.
۵.۱۱ اثبات اعتبار
تخصیص کلی
Universal Instant-iation
U.I.
در نظریه سورها یک قاعده استنتاج که استنتاج معتبر هر مورد جانشینی یک تابع گزارهای را از سور عمومی آن مجاز میکند.
تعميم کلی
Universal Generali-zation
U.G.
در نظریه سورها، یک قاعده استنتاج که استنتاج معتبر یک عبارت سور دار عمومی یا عام را از عبارتی که بعنوان درست برای فرد انتخابی دلخواه مجاز میکند.
تخصيص وجودی
Existential Instant-iation
E.I.
در نظریه سورها، یک قاعده استنتاج که میگوید (با برخی محدودیت) میتوان از سور وجودی یک تابع گزارهای بطور معتبر درستی مورد جانشین آن را برحسب هر ثابت انفرادی که پیشتر در متن (برهان) رخ نداده باشد استنتاج کرد.
تعمیم وجودی
Existential General-ization
E.G.
در نظریه سورها یک قاعده استنتاج که میگوید از هر مورد جانشین درست یک تابع گزارهای میتوان بطور معتبر سور وجودی آن تابع را استنتاج کرد.
برای ساختن برهان صوری اعتبار آن استدلالهايی، كه اعتبارشان به ساختار داخلی گزارههای غیرمرکب بكاررفته درآنها وابسته است، بايد فهرست قواعد استنتاج خود را گسترش دهيم. برای اینکار، فقط به چهار قاعده بيشتر از آنچه داریم نیاز داریم. در ادامه این قسمت، هر یک از این چهار قاعده را در رابطه با استدلالی که نیازمند به آن است معرفی خواهیم کرد.
به اولين استدلال كه در اين فصل آمد توجه نماييد:
«همه انسانها فانی هستند.
سقراط انسان است.
بنابراين سقراط فانی است.»
اين استدلال بصورت زير نمادين میشود:
(P۱): (x)(Hx ⊃ Mx)
(P۲): Hs
∴ Ms
اولين مقدمه تصديق درستی سور عمومی تابع گزارهای Hx⊃Mx است. از آنجا كه سور عمومی يك تابع گزارهای درست است اگر و فقط اگر همه موردهای جانشينی آن درست باشند، بنابراین از مقدمه اول، هر مورد جانشينی دلخواه تابع گزارهای Hx⊃Mx را میتوان نتيجه گرفت. بويژه مورد جانشين Hs⊃Ms نیز نتیجه میشود. از اين و مقدمه دوم Hs، نتيجه Ms بطور مستقيم بوسيله قياس استثنائیM.P. بدست میآيد.
اگر اين را كه میگوید: هر مورد جانشين يك تابع گزارهای میتواند بطور معتبر از سور عمومی آن استنتاج شودــ را به فهرست قواعد استنتاج خود اضافه كنيم، آنگاه میتوانیم برهان صوری استدلال داده شده را با مراجعه به فهرست صورتهای استدلالی معتبر مقدماتی گسترشيافته خود بیاوریم. اين قاعده جديد استنتاج، اصل تخصیص کلی➥ با كوته سازی UI است. با كارگرفتن حرف يونانی نو(ν) بعنوان نشان دهنده هر نماد منفرد، هر چه که باشد، اين قاعده جديد را میتوان اینگونه معرفی کرد:
۱- تخصیص کلی / Universal Instantiation
UI: (x)Φx
∴ Φν ( یک نماد انفرادی استν)
حالا میتوانیم برهان صوری اعتبار را به شیوه زير بنویسیم:
۱. (x)(Hx ⊃ Mx)
۲. Hs
∴ Ms
۳. Hs ⊃ Ms ۱, UI
۴. Ms ۳, ۲, M.P.
گرچه با اضافه كردن UI ابزار برهانی ما بطور قابل ملاحظه قویتر شدهاست ولی هنوز بيشتر از اين نياز است. نياز به قواعد بيشتر برای اداره سورها که برخاسته از استدلالهايی چون ــ «همه انسانها فانی هستنند. همه يونانیها انسان هستند. بنابراين همه يونانيها فانی هستند.» ــ است. برگردان نمادين اين استدلال به صورت زير
(x)(Hx ⊃ Mx)
(x)(Gx ⊃ Hx)
∴ (x)(Gx ⊃ Mx)
است:
در اينجا مقدمات و نتيجه هر دو بجای گزاره شخصی، گزارههای عام هستند و همينطور سوردار شده عمومی توابع گزارهای، بجای موردهای جانشينیشان حضور دارند. از دو مقدمه و کارزدن UI، میتوان بطور معتبر گزارههای شرطی دوگانه زير را استنتاج كرد:
| Ga ⊃ Ha Ha ⊃ Ma | Gb ⊃ Hb Hb ⊃ Mb | Gc ⊃ Hc Hc ⊃ Mc | Gd ⊃ Hd Hd ⊃ Md | ... ... |
و با بكاربردن متوالی اصل قياس شرطی H.S. نیز میتوان نتايج زير را بطور معتبر استنتاج نمود:
| Ga ⊃ Ma | Gb ⊃ Mb | Gc ⊃ Mc | Gd ⊃ Md | ... |
اگر d , c, b, a, … همه افرادی بودند كه وجود داشتند، آنگاه پیآمد آن اين بود كه با توجه به درستی مقدمات، همه موارد جانشينی تابع گزارهای Gx⊃Mx بطور معتبر قابل نتیجهگرفتن بودند. از آنجايی كه سور عمومی يك تابع گزارهای درست است اگر و فقط اگر همه موردهای جانشين آن درست باشند، میتوانستيم در ادامه درستی(x)(Gx⊃Mx) که همان نتيجه استدلال داده شده است را نتيجه بگيريم.
پاراگراف قبل را میتوان بعنوان يك برهان غيرصوری استدلال دادهشده درنظر گرفت، كه در آن اصل قياس شرطی و دو اصل حاكم بر سورها مورد استناد قرار گرفتهاند. اما اين یک وصف دنبالهای طولانی و نامعين از گزاره است، یعنی: فهرست همه موردهای جانشينی دو تابع-گزارهای در مقدمات، كه بطور کلی سوردار شدهاند. يك برهان صوری نمیتواند شامل وضعیت نامعين بودن باشد، كه ممکن است حتی دنبالهای نامتناهی از گزارهها نيز باشد. لذا بايد درپی یک روش برای بيان اين دنباله بطور نامعين طولانی، به صورتی متناهی و بگونه معين بود.
یک روش، که در رياضيات مقدماتی معمول است، راهی برای انجام اینکار به ذهن میآورد. وقتی يك هندسه دان میخواهد ثابتكند همه مثلثها دارای ويژگیهای مشخصی هستند، وی ممکن است عبارات خود را اينگونه آغازکند: «مثلث دلخواه ABC را در نظر میگيريم.» سپس وی آغاز به دليل آوردن درباره مثلث ABC نماید و ثابت كند این مثلث دارای ويژگیهای مورد نظر است. از اين، وی نتيجه میگيرد كه همه مثلثها دارای اين ویژگیها هستند. چه توضيح و توجيهی برای نتيجه پايانی وی است؟ ولو آنکه، بپذيريم اين مثلث بخصوص دارای آن ویژگیها است، چرا از آن، اینكه همه مثلثها دارای آن ویژگیها هستند، بدست میآيد؟ پاسخ اين پرسش آسان است. وقتی هيچ فرضی بجز مثلث بودن در باره مثلث ABC مورد نظر نیست، آنگاه نماد "ABC" میتواند دلالت كننده به هر مثلث كه بخواهيد باشد. استدلال هندسه دان ثابت میکند که هر مثلث دارنده ویژگیهای مطرح است، و اگر هر مثلث دارنده آنهاست آنگاه همه مثلثها دارنده آنهایند. ما نیز مشابه هندسه دان در صحبت از «هر مثلث مفروض دلخواه ABC»، يك نشانگذاری را معرفی میكنيم. اين كار مانع از ادعای فهرست كردن تعداد نامعين يا نامتناهی موردهای جانشين برای يك تابع-گزارهای میشود. چرا كه ما بهجای آن، صحبت درباره هر مورد جانشين تابع گزارهای خواهيم كرد.
ما حرف كوچك y (كه تاكنون بکار نرفته) را بكار میبریم تا نمايانگر هر شئ انفرادی مفروض / منتخب دلخواه باشد. ما آن را مشابه روشی كه هندسه دادن حروف ABC را بكار میبرد بكار خواهيم برد. از آنجاكه، درستی هر مورد جانشين يك تابع گزارهای قابل دست آوردن از مسوّر (سوردار شده) عمومی آن است، میتوانيم آن مورد جانشينی كه حاصل از جانشينی y بجای x است را استنتاج نماييم، كه در آن y نمايانگر «هر» شئی انفرادی «مفروض / منتخب دلخواه» است. با توجه به آنچه گفته شد، اكنون میتوانيم برهان صوری اعتبار استدلال داده شده را آنگونه كه میآيد آغاز كنيم:
در بالا از مقدمات، گزاره Gy⊃My را نتيجه گرفتيم، كه در عمل با توجه بهاينكه y نمايانگر «هر شئی مفروض (منتخب) انفرادی» است، درستی هر مورد جانشينی تابع گزارهای Gx⊃Mx را تصديق میكند. از آنجا كه هر مورد جانشين درست است، همه موردهای جانشين بايد درست باشند و بنابراين مسور عمومی تابع-گزارهای نيز بايد درست باشد. میتوان اين اصل را به فهرست قوانين استنتاج خود اضافه كنيم و آن را اينگونه بيان نماييم: از مورد جانشين هر تابع گزارهای برحسب نام هر شئ انفرادی منتخب دلخواه، میتوان اعتبار مسوّر عمومی آن تابع گزارهای را استنتاج نمود. چون اين اصل جديد مجوز تعميم، يعنی انتقال از يك مورد جانشين خاص به تعميم یافته يا به عبارت دیگر، مسوّر کلی آن، به ما میدهد از آن بعنوان اصل تعميم کلی رجوع و آن را با "UG" كوته سازی میکنیم. اين اصل بصورت زير بيان ميشود.
۲- تعميم کلی / Universal Generalizatio
UG: Φy
∴ (x)Φx
y نمایانگر «هرشئی انتخابی دلخواه» است.
حالا میتوان خط ششم و پايانی برهان صوری را كه آغاز كرده بوديم مطابق
۶. (x)(Gx ⊃ Mx) ۵, U.G.
بنویسیم و آن را توجیه نماییم.
برای ادامه، بحث پیشین را مرور میکنیم. در برهان هندسه دان تنها فرض گرفته شده برای ABC اين است كه آن يك مثلث است؛ و لذا آنچه كه ثابت شد برای ABC درست است برای هر مثلثی نيز درست است. در برهان ما، تنها مفروض برای y شئ انفرادی بودن آن است، لذا آنچه كه ثابتشد برای y درست است، برای هر شئی انفرادی ديگر نيز درست است. نماد y يك نماد انفرادی اما بسيار مخصوص است. اين نماد نوعاً با كارزدن U.I در يك برهان حضور مییابد، ولی فقط حضور y مجوز كارزدن U.G را میدهد.
اينجا يك استدلال معتبر آمده است كه اثبات اعتبار آن به U.G و بعلاوه به U.I نیاز دارد: «هيچ انسان كامل نيست. همه يونانيان انسان هستند. بنابراين هيچ يونانی كامل نيست➥».
برهان صوری اعتبار آن به صورت زير است:
| (x)(Hx ⊃ ~Px) | ۱. | |
| (x)(Gx ⊃ Hx) | ۲. | |
| (x)(Gx ⊃ ~Px) | ∴ | |
| ۱, U.I | Hy ⊃ ~Py | ۳. |
| ۲, U.I | Gy ⊃ Hy | ۴. |
| ۴, ۳, H.S. | Gy ⊃ ~Py | ۵. |
| ۵, U.G | (x)(Gx ⊃ ~Px) | ۶. |
ممكن است به نظر برسد آنچه گفته شد تا اندازهای تصنعی است. يعنی اصرار به تمايز دقيق قائل شدن بين (x)Φx و Φy، یعنی كه نباید با آنها يكسان رفتاركرد و هر يك بايد از ديگری بوسيله U.I و U.G استنتاج شود، پافشاری به تمايزی است که در آن چیزی موجب تفاوتی نیست. ولی قطعا يك تمايز صوری بين آنها وجود دارد. گزاره (x)(Hx⊃Mx) يك گزاره ساده است حال آنكه گزاره Hy⊃My يك گزاره مرکب است که شرطی نیز است. از دو گزاره غيرمركب:
(x)(Hx⊃Mx) و (x)(Gx⊃Hx)
هيچ استنتاج مرتبطی با كارزدن فهرست اصلی نوزده قاعده نمیتوان استخراج كرد. اما از گزارههای مركب Gy⊃Hy و Hy⊃My نتيجه نشان دادهشده بوسيله قیاس شرطی حاصل میشود. اصل U.I بكار بسته شده تا از گزارههای غيرمركب كه قواعد پيشين استنتاجی ما بطور مفيد به آنها كارزدنی نيستند، گزارههای مركبی بدست آوریم، بهقسمی كه، قواعد استنتاجی پيشين، برای استخراج نتيجه موردنظر، بتوانند به آنه بكار زده شوند. از اين رو، اصول تعميم ابزار منطقی ما را گستردهتر میسازد تا آن را توانمند به برآورد اعتبار استدلالهايی سازد كه به ضرورت مستلزم گزارههای غيرمركب (تعمیم یافته) هستند و نيز بعلاوه انواع ديگر استدلال (سادهتر) كه در فصل پيشين به آنها اشاره شد. از سوی ديگر نيز بايد يك هم ارزی منطقی بين (x)Φx و Φy وجود داشته باشد وگرنه قاعدههای U.I و U.G معتبر نمیبودند. هردو، يعنی هم تفاوت و نیز همارزی منطقی برای هدف ما كه برآورد اعتبار استدلالها از طريق رجوع به يك فهرست از قواعد استنتاج است، مهم است. الحاق U.I و U.G بهاين فهرست آنرا بطور قابل ملاحظه تواناتر میسازد.
وقتی متوجه استدلالهای درگير با گزارههای وجودی میشويم، اين فهرست هنوز کافی نیست و بايد بيشتر گسترش یابد. مثال راحتی كه با آن آغاز می كنيم، به اين قرار است: «همه بزهكاران بدسگال هستند. بعضی انسان بزهكار است. بنابراين بعضی انسان بدسگال است». اين استدلال مطابق زير نمادين می شود.
(P۱): (x)(Cx ⊃ Vx)
(P۲): (Ex)(Hx • Cx)
∴ (Ex)(Hx • Vx)
سور وجودی يك تابع گزارهای درست است، اگر و تنها اگر آن تابع گزارهای حداقل يك مورد جانشینی درست داشته باشد و لذا هرچه باشد ويژگی نشانداده توسط Φ، آنگاه (∃x)Φx میگويد حداقل يك شئی انفرادی هست كه دارای ويژگی Φ است. اگر يك ثابت منفرد قبلا در زمينه (متن برهان) بكار نرفته باشد میتوان آن را بكار برد تا شئای انفرادی را نشان دهد كه دارنده ويژگی Φ است و يا در صورت تعداد بيشتر شئ انفرادی، به عنوان نشان دهنده يكی از آنها باشد كه ویژگی Φ را دارد. وقتی بدانيم يكی از اين اشياء انفرادی بهفرض a است آنگاه داریم Φa، که يك مورد جانشين درست تابع گزارهای Φx است. از اين رو اصل زير را به فهرست قوانين استنتاج خودی اضافه میكنيم: از سور وجودی يك تابع گزارهای میتوان درستی مورد جانشين آن را برحسب هر ثابت منفرد (بجز از y)، كه رويدادی پیشین در زمينه نداشته است، نتيجه گرفت. اين قاعده جديد استنتاج، اصل تخصيص وجودی است، كه كوتهشده آن نيز E.I است. اين اصل به گونه زير بيان می شود:
۳- تخصيص وجودی / Existential Instantiation
EI: (∃x)Φx
∴ Φυ
با پذيرش قاعده استنتاج E.I میتوانيم اثبات اعتبار استدلال گفته شده را آغاز كنيم.
| (x)(Cx ⊃ Vx) | ۱. | |
| (∃x)(Hx • Cx) | ۲. | |
| (∃x)(Hx • Vx) | ∴ | |
| ۲, E.I. | Ha • Ca | ۳. |
| ۱, U.I. | Ca ⊃ Va | ۴. |
| ۳, Com. | Ca • Ha | ۵. |
| ۵, Simp. | Ca | ۶. |
| ۴, ۶, M.P. | Va | ۷. |
| ۳, Simp | Ha | ۸. |
| ۸, ۷, Conj. | Ha • Va | ۹. |
تا اينجا، Ha•Va را نتيجه گرفتيم كه مورد جانشين تابع گزارهای است كه سور وجودی آن همان است که بوسيله نتيجه ادعا شده. از آنجا كه مسوّر وجودی يك تابع-گزارهای درست است، اگر و فقط اگر حداقل يك مورد جانشينی درست داشته باشد، اين اصل را نیز به فهرست قواعد میافزائیم، که میگويد ــ از هر مورد جانشينی درست يك تابع-گزارهای میتوان مسوّر وجودی آن تابع گزارهای را بطور معتبر استنتاج كرد. اين چهارمين و آخرين قاعده استنتاج، اصل تعمیم وجودی با كوتهشده E.G است كه به گونه زير بيان ميشود.
۴- تعمیم وجودی / Existential Generalization
EG: Φυ
∴ (∃x)(Φx)
(که در آن υ یک نماد انفرادی است)
دهمین و آخرين خط اثباتی را كه شروع كردهايم، اكنون میتوان بهگونه زير نوشت و آنرا موجه کرد:
۱۰ (Ex)(Hx • Vx) ۹, E.G.
نياز به محدوديت در كاربرد E.I، كه به آن اشاره شد، را میتوان با ملاحظه استدلال آشكارا نامعتبر كه به دنبال آمده است دريافت. «بعضی تمساحها در اسارت نگهداری میشوند. بعضی پرندهها در اسارت نگهداری میشوند. بنابراين بعضی تمساحها پرنده هستند». اگر غافل شويم و توجه به محدوديت اعمالی بر E.I نكنيم كه میگويد –مورد جانشين يك تابع گزارهای كه بوسيله E.I از سور وجودی آن تابع استنتاج میشود، فقط میتواند شامل نماد انفرادیای (بجز y) باشد، كه دارای رويداد پيشين در زمينه نباشد- آنگاه ممكن است ادامه دهيم و يك «برهان» برای اين استدلال نامعتبر بسازيم. اين چنين «برهان» خطادار میتواند به گونه زير باشد:
| (∃x)(Ax • Cx) | ۱. | |
| (∃x)(Bx • Cx) | ۲. | |
| (∃x)(Ax • Bx) | ∴ | |
| ۱, E.I. | Aa • Ca | ۳. |
| ۲, E.I. (!خطا) | Ba • Ca | ۴. |
| ۲, Simp. | Aa | ۵. |
| ۴, Simp. | Ca | ۶. |
| ۵, ۶, Conj. | Aa • Ca | ۷. |
| ۷, E.G. | (∃x)(Ax • Bx) | ۸. |
خطا در اين برهان در خط چهارم رخ داده است.
از مقدمه دوم، (∃x)(Bx•Cx)، میدانيم كه حداقل يك شئی هست كه هم پرنده است و نيز در اسارت نگهداری میشود. اگر آزاد بوديم تا در خط چهارم نام آنرا a بگذاريم، روشن است كه نيز میتوانستيم مدعی Ba•Ca شویم. اما آزاد نيستيم تا گمارشی مثل «a» انجام دهيم، چرا كه هم اكنون، «a» پيش دستی كرده و در خط سوم وظيفهمند بعنوان نام يك تمساح كه در اسارت نگهداری میشود است. برای پرهيز خطاهايی از اين قسم بايد در هر جا كه E.I را بكار میبريم محدوديت گفتهشده را رعايت كنيم. بحث پيشترگفته، بايد روش ساخته باشد، در هر اثبات كه نيازمند بكار زدن E.I و U.I هر دو است، آنگاه هميشه E.I بايد ابتدا بكارزده شود.
برای حالت های پيچيدهتر استدلال، بخصوص آنها كه مستلزم حضور رابطه هستند، محدوديتها بيشتری براين چهار قاعده بايد اعمال شود. اما برای استدلالهايی از قسم حاضر، كه به طور سنتی قیاس حملی ناميده میشوند محدوديتهای گفتهشده كفايت پرهيز از خطا را میكنند.
| قواعد چهار گانه سور ها | |||
| نام | کوته سازی | صورت | کارکرد |
| تخصیص کلی Universal Instantiation | U.I. | (x)Φx ∴ Φυ (υ نماد هر منفرد میتواند باشد.) | ۱- هر مورد جانشينی يك تابع-گزارهای میتواند از سور عمومی آن استنتاج شود. |
| تعمیم کلی Universal Generalization | U.G. | Φy ∴ (x)Φx (y نمادی برای هر منفرد دلخواه منتخب است.) | ۲- از مورد جانشينی يك تابع گزارهای برحسب نام هر منفرد دلخواه انتخابی میتوان بطور معتبر سور عمومی آن صورت گزارهای را استنتاج نمود. |
| تخصیص وجودی Existential Instantiation | E.I. | (∃x)Φx ∴ Φυ (υ میتواند هر ثابت منفرد، بجز y، باشد که رویدادی از آن پیشتر در زمینه نیامده باشد. | ۳- از سور وجودی یک تابع گزاره ای میتوان درستی مورد جانشینی آن را نسبت به هر ثابت منفرد (بغیر از y) که رویدادی از آن ثابت انفرادی پیشتر در زمینه رخ نداده باشد، استنتاج کرد. |
| تعمیم وجودی Existential Generalization | E.G. | Φν ∴ (∃x)Φx (υ نماد هر منفرد میتواند باشد.) | ۴- از مورد جانشينی درست يك تابع گزارهای میتوان سور وجودی آن تابع گزارهای را بطور معتبر استنتاج نمود. |
تمرین
الف- برای هر يك از استدلالهای زير يك برهان صوری اعتبار تشكيل دهيد.
۱- مثال:
(x)(Ax ⊃~Bx)
(∃x)(Cx•Ax)
∴ (x)(Cx•~x)
حل:
نتيجه اين استدلال يك گزاره است كه مسور وجودی است. از اينجا به آسانی روشن میشود كه آخرين مرحله عبارت از كار زدن EG (تعميم وجودي) خواهد بود. برای رسيدن به خط مورد نياز، باید برای مقدمات موردجانشین بسازیم(تخصيص برای مقدمات کنیم). اين كار را با كارزدن EI (تعميم وجودي) به مقدمه دوم و سپس كار زدن UI (تخصيص کلی) به مقدمه اول انجام میدهيم. محدوديت اعمالی بر كارزدن EI ما را ملزم میكند تا EI را قبل از UI بكار بزنيم، به قسمی كه بتوانيم يك ثابت منفرد يكسان، بفرض a را، برای هر دو بكار ببريم. برهان بگونه زير میتواند ساختهشود:

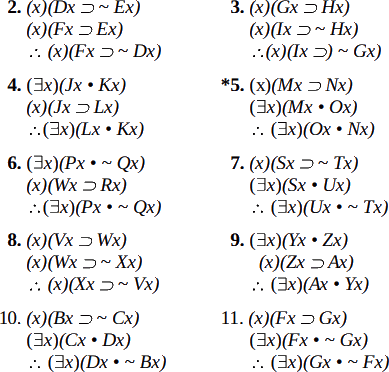
ب- برای هر يك از استدلال های زير يك برهان صوری اعتبار تشكيل دهيد و در هر حالت نشانه گذاری پيشنهادی را بكار بريد.
۱*- هيچ قهرمان كرم كتاب [خيلی كتابخوان] نيست. كاوه يك كرم كتاب است. بنابراين كاوه يك قهرمان نيست. (Ax,Bx,c)
۲- همه رقصندهها سرزنده هستند. بعضی شمشيربازها سرزنده نيستند. بنابراين بعضی شمشيربازها رقصنده نيستند. (Dx,Ex,Fx)
۳- هيچ قماربازی خوشحال نيست. بعضی ايدهآليستها خوشحالند. بنابراين بعضی ايدهآليستها قمارباز نيستند. (Gx,Hx,Ix)
۴- همه جوكرها پست هستند. هيچ پستی خوشبخت نيست. بنابراين هيچ جوكری خوشبخت نيست. (Jx,Kx,Lx)
۵- همه كوهنوردان دوست منش هستند. بعضی قانون گريزها كوهنورد هستند. بنابراين قانون گريزها دوست منش هستند. (Mx,Nx,Ox)
۶- فقط صلح طلبها طرفدار محيط زيست هستند. مذهبیهايی هستندكه طرفدار محيط زيست هستند. بنابراين صلح طلبها گاهی مذهبی هستند.
۷- گوشبری دزدی است. هيچ كس مگر محرومان دزد هستند. بنابراين گوشبرها هميشه محروم هستند.
۸- هيچ ويولونيستی نيست كه ثروتمند نباشد. سه تار نواز ثروتمند وجود ندارد. بنابراين هيچ ويولونيست سه تارنواز نيست.
۹- هيچ كس مگر دلاوران شايسته انصاف هستند. فقط سربازان دلاور اند بنابراين انصاف شايسته فقط سربازان است. (Sx: x سزاوار انصاف است,Dx: x دلاور است,Sx: x سرباز است)
۱۰*- جوينده يابنده است. سارا چيزی نيافته است بنابراين سارا جوينده نيست.
۱۱-آن: هيچ جباری چنان درندهخو نيست كه چيزی از حس ترحم نداند.
گلوكستر: من چنين كسی را نمیشناسم بنابراين جبار نيستم. (Bx,Px,g) ــ ويليام شكسپير-ريچارد سوم نمايش 1 صحنه 2

■ ■ ■ ■ ■
