جهان ممکن، مدل و اثبات عدم اعتبار
منطق محمولات
درآمد به منطق فصل ۱۱ قسمت ۶
در قسمت پیشین ۴ قاعده استنتاج ۱- تخصیص کلی ۲- تعميم کلی ۳- تخصيص وجودی و ۴- تعمیم وجودی در منطق محمولات برای اثبات اعتبار صورت استدلال معرفی شد. اما چه برای اثبات بیاعتباری؟ بنابراین، نکته کلیدی این قسمت در مفهوم مدل و جهان ممكن نهفته است و اینکه، یک صورت استدلال فقط و فقط وقتی معتبر استکه همه جهانهای ممکن (هر تعبیر) مدل آن باشند. بنابراین، برای اثبات بیاعتباری یک صورت استدلال کافیست جهان ممکنی (تعبیری) یافت که مدل صورتِ استدلال مورد وارسی نباشد.
۶.۱۱ جهان ممکن، مدل و اثبات عدم اعتبار
تعبیر
Interpre-tation
مراد از تعبیر روندی است که به صورت های گزارهای معنایی منتسب کند که به موجب آن، آن صورت گزارهای دارای مقدار ارزش درست و یا نادرست گردد.
برای مثال،
به موجب روند جدول-ارزش چهار تعبیر برای صورت شرطی،
p⊃q،
ممکن است که فقط یک تعبیر مقدار ارزش صورت را نادرست برمیآورد.
به مقادیر ارزش مقادیر معنایی / سمانتیکی نیز
میگویند.
مدل
Model
یک مدل برای یک صورت گزارهای تعبیری است که به موجب آن تعبیر، آن صورت دارای مقدار ارزش درست گردد.
برای اثبات بیاعتباری استدلالی كه شامل عبارتهای گزارهای سوردار است، میتوان از روش وازنش همسنجانه استفاده کرد. برای مثال استدلال زیر را در نظر بگیرید:
«همه محافظه كاران با اعضای دولت مخالف هستند؛ بعضی نمايندگان با اعضای دولت مخالف هستند؛ بنابراين بعضی نمايندگان محافظهكار هستند.»
این استدلال را میتوان با قیاس آن با استدلال آشکارا نامعتبر زیر:
«همه گربهها حيوانند؛ بعضی سگها حيوانند؛ بنابراين بعضی سگها گربهاند.»
ثابت کرد که معتبر نیست.
این استدلال معتبر نیست، زیرا دانسته است که مقدمات آن درست و نتيجه آن نادرست است. اما تدبير چنين فراسنجی هميشه آسان نيست، بنابراین باید در پی روشی با كارايی بيشتر رفت.
در فصل قبل (۱۰) روشی را برای اثبات بیاعتباری استدلالهای شامل گزاره های تابع–ارزش گسترش دادیم. اين روش عبارت از گمارش مقادیر ارزش به مولفههای ساده عبارتهای گزارهای استدلال بود، به قسمی كه اين گمارش مقدمات را درست و نتيجه را نادرست سازد. اين روش را میتوان به استدلالهايی كه در آنها سورها بكار میروند نيز سرايت داد. اين اقتباس مستلزم فرض عام ماست كه حداقل يك شئ انفرادی وجود دارد. برای آنكه يك استدلال شامل سورها معتبر باشد، وقتی حداقل يك شئ انفرادی وجود دارد، نباید ممكن باشد كه مقدمات آن درست و نتيجه آن نادرست باشد.
فرض كلی، يعنی وجود حداقل يك شئ انفرادی وقتی پذیرفتنی است، که اگر دقيقا يك شئ انفرادی وجود داشته باشد يا دقيقا دو شئ انفرادی وجود داشته باشد يا دقيقا سه شئ انفرادی وجودی باشد و همینطور برای بیشتر از سه شئ.
وقتی هرکدام از اين فرضها درباره تعداد دقیق اشياء انفرادی پذیرفته شود، آنگاه يك همارزی بين گزارههای عام و تركيبهای تابع-ارزشی گزارههای انفرادی وجود خواهد داشت.
اگر دقيقا يك شئ انفرادی به فرض a وجود داشته باشد آنگاه
(x)Φx  Φa
Φa  (∃x)Φx
(∃x)Φx
اگر دقيقا دو شئ انفرادی، مثل a و b وجود داشته باشد آنگاه
(∃x)Φx
 [Φa ∨ Φb] و (x)Φx
[Φa ∨ Φb] و (x)Φx
 [Φa • Φb]
[Φa • Φb]
اگر دقيقا سه شئ انفرادی وجود داشته باشد، گيريم a و b و c آنگاه
(∃x)Φx
 [Φa ∨
Φb ∨ Φc] و (x)Φx
[Φa ∨
Φb ∨ Φc] و (x)Φx
 [Φa •
Φb •Φc]
[Φa •
Φb •Φc]
در حالت كلی اگر دقيقا n شئ انفرادی، گيريم a, b, c,… ,n آنگاه
(x)Φx
 [Φa •
Φb • Φc • … •
Φn]
[Φa •
Φb • Φc • … •
Φn]
و
(∃x)Φx
 [Φa ∨ Φb ∨
Φc ∨…∨Φn]
[Φa ∨ Φb ∨
Φc ∨…∨Φn]
همه اين دوشرطیها به عنوان نتيجه تعريف ما از سورهای عمومی و وجودی درست هستنند. بعلاوه توجه داشته باشید که در اينجا هيچ استفادهای از قواعد چهار گانه سورها، که در قسمت قبل شرح داده شد، نشده است.
■ تعبیر، مدل و جهانهای ممکن

يك استدلال دارای سور معتبر است اگر و فقط اگر بشرط وجود حداقل يك شئ انفرادی، صرف نظر از تعداد آنها معتبر باشد. بنابراين يك استدلال كه در آن سور بكار رفته ثابت میشود نامعتبر است اگر يك جهان ممكن (تعبیر) یا يك مدل با حداقل يك شئ انفرادی باشد، به قسمیكه برای آن مدل مقدمات آن استدلال درست و نتيجه آن نادرست باشد. به این استدلال «همه اجيرشدگان وابسته هستند. همه سربازان اجيرشده نيستند. بنابراين هيچ سربازی وابسته نيست.» توجه كنيد. آن را میتوان مطابق زير نمادين كرد.
(x)(Mx ⊃ Ux)
(x)(Gx ⊃ ~Mx)
∴ (x)(Mx ⊃ ~Ux)
اگر فقط يك شئ انفرادي، گيريم a، وجود داشته باشد، آنگاه اين استدلال منطقاً همارز است با
(P۱): Ma ⊃ Ua
(P۲): Ga ⊃ ~Ma
∴ Ma ⊃ ~Ua.
با گمارش مقدار ارزش درست به Ga و Ua و نادرست به Ma میتوان ثابت كرد كه استدلال دوم نامعتبر است. (اين گمارش مقادير-ارزش يك راه كوتاه نويسی برای وصف مدل مورد ملاحظه است که شامل فقط يك شئ انفرادی a، که سرباز و نیز وابسته اما اجیر نیست، است.) از اینرو استدلال اصلی برای یک مدل که دقیقا دارای یک شئ انفرادی است، معتبر نيست. بههمين شيوه، بیاعتباری استدلال آمده در اول اين قسمت را میتوان ثابت کرد، یعنی با وصف يك مدل، که دقيقا شامل یك شئ انفرادی a باشد و نیز به Da و Aa مقدار ارزش درست و به Ca مقدار ارزش نادرست➥ گمارده شود.
بعضی استدلالها - برای مثال
(∃x)Fx
∴ (x)Fx
ممكن است برای هر مدل كه در آن دقيقا يك شئ انفرادی وجود دارد معتبر باشد اما برای يك مدل كه تعداد دو يا بيشتر شئ انفرادی است نامعتبر باشند. اين استدلالها نيز بايد نامعتبر به حساب آيند، زيرا يك استدلال معتبر بايد تا آنجا كه حداقل يك شئ انفرادی وجود دارد صرف نظر از اينكه چه تعداد از اين اشياء هست، معتبر باشد. مثال ديگر از اين نوع استدلال عبارتست از : «همه سگهایگله مهربان هستند. بعضی سگهایگله سگهای محافظ هستند. بنابراين همه سگهای محافظ مهربان هستند.» برگردان نمادين آن به قرار زير است:
(P۱): (x)(Cx ⊃ Ax)
(P۲): (∃x)(Cx • Wx)
∴ (x)(Wx ⊃ Ax)
برای يك مدل كه فقط دارای يك شئ انفرادی، a، است استدلال بالا منطقاً همارزاست با
(P۱): Ca ⊃ Aa
(P۲): Ca • Wa
∴ Wa ⊃ Aa
كه معتبر است. اما برای مدلی كه دارای دو شئ انفرادی a و b است منطقا معادل است با:
(P۱): (Ca ⊃ Aa)• (Ca ⊃ Aa)
(P۲): (Ca • Wa) ∨ (Ca • Wa)
∴ (Wa ⊃ Aa) • (Wa ⊃ Aa)
كه با گمارش مقدار ارزش درست به Ca و Aa و Wa و Wb و مقدار ارزش نادرست به Cb و Ab ثابت میشود كه نامعتبر است. از اينرو استدلال اصلی برای مدلی كه دقيقا دارای دو شئ انفرادی است معتبر نيست و بنابراين نامعتبر است. برای هر استدلال نامعتبر از این نوع کلی، میتوان مدلی که به تعداد معینی شیئ انفرادی دارد را وصف کرد، بگونهای که همارز منطقی استدلال تابع-ارزشی باشد که میتوان بیاعتباری آنرا با گمارش مقادیر ارزش نشانداد.
بايد مجددا تاكيد كنيم كه: در حركت از يك استدلال داده شده شامل گزارههای عام بسوی يك استدلال تابع-ارزش (كه برای يك مدل معين با استدلال دادهشده منطقا همارز است) هيچ كدام از چهار قاعده سورها به كارزده نشدهاند. بجای آن هر عبارت تابع-ارزش استدلال همارز منطقی با گزاره عام نظير در استدلال دادهشده است و اين همارزی پيشتر در اين قسمت و در اينجا بوسيله دو شرطیها كه درستی منطقی آنها نتيجه مستقيم تعاريف سورهای عمومی و وجودی است، پيكربندی شده است.
روند برای اثبات بیاعتباری استدلالهای دارای گزارههای عام مطابق یا آنچه است كه درپی میآيد. يكم، يك مدل يك عنصری، كه شامل فقط شئ انفرادی a است، را درنظر بگيريد. سپس استدلال تابع-ارزش منطقا همارز را برای این مدل بنويسيد، بگونهای كه اين استدلال عبارت باشد از حاصل حركت از هر گزاره عام(تابع گزارهای مسور) به سمت موردهای جانشينی تابع-گزارهای برحسب a. اگر بیاعتباری اين استدلال تابع-ارزش را میتوان با گمارش مقادير ارزش به مولفههای گزارهای ساده آن اثبات كرد، آنگاه همين برای بیاعتباری استدلال اصلی كفايت میكند. اگر چنين نشد، آنوقت يك مدل دو عنصری كه شامل اشيائ انفرادی a و b است را درنظر بگيريد. برای بدست آوردن استدلال تابع-ارزش منطقا همارز، برای اين مدل بزرگتر، میتوان به هر مورد جانشينی اصلی نسبت به a، يك مورد جانشين جديد تابع-گزارهای يكسان ولی نسبت به b، متصل كرد. اين «اتصال» بايد مطابق با همارزیهای منطقی گفتهشده در اين قسمت باشد، يعنی هرجا كه استدلال شامل يك تابع-گزارهای مسور عمومی، یعنی
(x)Φx
است، مورد جانشين جديد[یعنی Φb] بايد توسط رابط عطف("•") بامورد جانشين اول a تركيب شود؛ ولی هرجا كه استدلال شامل يك تابع گزارهای مسور وجودی، یعنی
(∃x)Φx
است، مورد جانشين جديد[یعنی Φb] بايد با مورد جانشين اول[یعنی Φa]توسط رابط فصل("∨")تركيب شود. استدلال قبل اين روند را نمايش میدهد. اگر بیاعتباری اين استدلال تابع-ارزش جديد را میتوان با گمارش مقادير ارزش اثبات كرد آنگاه همين برای بیاعتباری اصلی كفايت میكند. اگر چنين نشد، آنوقت يك مدل سه عنصری دارای اشياء انفرادی a, b, c را در نظر بگيريد و روند را بههمين ترتيب ادامه دهيد. هيچ يك از تمرينات كتاب نيازمند به مدلی با بيش از سه عنصر نيست.
تمرينات زير به مدلی با بيش از دو عنصر نياز ندارند.
الف. بیاعتباری موردهای زير را ثابت كنيد.
مثال:
(∃x)(Ax •
Bx)
(∃x)(Cx •
Bx)
∴ (x)(Cx ⊃ ~Ax)
حل:
ابتدا یک مدل (يا جهان ممکن، نشان داده در زیر بوسیله یک جعبه مستطیلی به رنگ سبز) بنا میکنیم که دارای دقيقا يك عنصر a باشد. بنابراين،
| صورت استدلالی | جهان ممکن | |
| (∃x)(Ax • Bx) (∃x)(Cx • Bx) ∴ (x)(Cx ⊃ ~Ax) | در a منطقاً هم ارز است با ⇐ | Aa • Ba Ca • Ba ∴ Ca ⊃ ~Aa |
بیاعتباری استدلال در اين مدل را بوسيله گمارش مقادير ارزش مطابق زير ثابت میکنیم:
| Aa | Ba | Ca |
| T | T | T |
ازآنجا كه ثابتشد اين استدلال در اين مدل غيرمعتبر است، نیز ثابت شده است كه استدلال نامعتبر است. بعبارت دیگر، a مدل این صورت استدلال نیست.
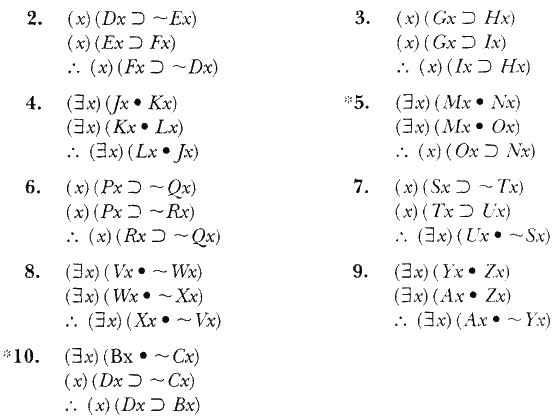
ب: بیاعتباری موارد زير را ثابت كنيد و در هر مورد نشان گذاری پيشنهادی را بكار ببريد.
۲. هيچ سياستمدار افراطی نيست. بعضی فناتيكها افراطی هستند. بنابراين بعضی ديپلماتها فناتيك نيستند
۳. همه ژنرالها زيبايند. بعضی روشنفكران زيبايند. بنابراين بعضی ژنرالها روشنفكرند.
۴. بعضی روزنامه نگاران پرمشغلههستند. بعضی پرمشغلهها خوشبخت نيستند.
۵*-بعضی سركشان پرسرصدا هستند. بعضی رسمیها پرسروصدا نيستند. بنابراين هيچ رسمی سركش نيست.
۶. بعضی پزشكان شارلاتان هستند. بعضی شارلاتانها مسئوليت پذير نيستند. بنابراين بعضی پزشكان مسئوليتپذير نيستند.
۷. بعضی سياستمداران رهبرند. بعضی رهبران سخنور نيستند. بنابراين بعضی سخنوران سياستمدار نيستند.
۸. هيچ كس مگر شجاعان سزاوار انصافند. هر سرباز شجاع است. بنابراين هيچ كس مگر سربازان سزاوار انصافند. (x:Dx شايسته انصاف است؛ x:Bx شجاع است؛ x:Sxسرباز است.)
۹. اگرچيزی متاليك باشد شكستنی است. زمينیهای شكستنی وجود دارند. بنابراين زمينیهای متاليك وجود دارند. (Mx,Bx,Dx)
۱۰*. دانشجويان عضوند. فقط اعضا میتوانند بيايند. بنابراين همه دانشجويان میتوانند بيايند. (Sx,Mx,Wx).

