گزارههای سنتی موضوع - محمول
منطق محمولات
درآمد به منطق فصل ۱۱ قسمت ۴
قسمت پیشین به نمادگذاری سور عمومی، سور وجودی، روابط آنها نیزنمایاندن این روابط در مربع تقابل جدید پرداخت. این قسمت تحلیل گزارههای حملی (قضیههای حملی در منطق قدیم) و روابط بین آنها در پرتو منطق جدید است.
۴.۱۱ گزارههای سنتی موضوع - محمول
با كاربرد سورهای عمومی و وجودی و با فهميدن مربع تقابل جدید (قسمت قبل)، که برای یادآوری در زیر بازنما شده است، میتوانيم چهار گزاره عام را كه بطور سنتی در خواندن منطق بدان تاكيد میشد تحليل و بطور دقيق در استدلال بكار بريم.
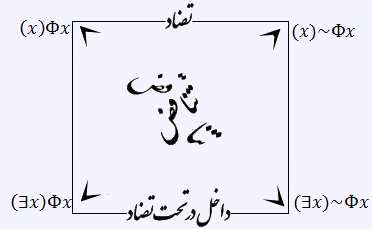
نمايش استاندارد اين چهار نوع در زير آمدهاند:
همه انسان فانی است. (موجب کلی: A)
هيچ انسان فانی نيست. (سالب کلی: E)
بعض انسان فانی است. (موجب جزئی: I)
بعض انسان فانی نیست. (سالب جزئی: O)
به هر یک از اين چهار نوع معمولاً با حرف آن رجوع میشود، یعنی به دو گزاره موجب با I ,A (از واژه لاتين AffIrmo - من تصديق میكنم) و به دو گزاره سلبی با O ,E (از واژه لاتين nEgO - من انكار میكنم.) رجوع میکنیم.➥ نمادسازی برای اين گزارهها بوسیله سورها ما را به مفهوم گستردتر یک تابع گزارهای میرساند.
ابتدا گزاره A «همه انسانها فانی هستند» را بررسی میکنیم و كار را با بازنویسیهای متوالی آن زیر آغاز میكنيم:
هرچه باشد شئ داده شده، اگر آن انسان است آنگاه آن فانی است.
در این بازنویسی دو مورد ضمير اشاره «آن» آشكارا به مقدم مشترك خود، يعنی واژه «شئ»، رجوع میكنند. مانند اوايل قسمت پیش، اين واژه دارای سه مورد رجوع يكسان (نامعین) است. آنها میتوانند بوسیله حرف x جایگرین شوند و گزاره به صورت زير بازنويسی شود:
برای هر x دادهشدهای اگر x انسان است آنگاه x فانی است.
حال اگر نمادگذاری پیشتر معرفی شده برای "اگر - آنگاه" را بکار ببریم، میتوان آنرا بصورت زیر نوشت:
[از چپ به راست]: x فانی است ⊂ x انسان است (برای هر x)
سرانجام چنانچه نمادسازی خود را برای توابع گزارهای و سورها بكاربريم آنگاه گزاره اصلی A بصورت زير نوشته میشود:
(x)(Hx ⊃ Mx)
در اين برگردان به نماد، گزاره A بعنوان سور عمومی گونهای تابع گزارهای جديد ظاهر گردیده.
عبارت Hx ⊃ Mx یک تابع گزارهای است كه موردهای جانشینی آن نه گزارههای ايجابی (موجب) و نه سلبی انفرادی هستند، بلكه آنها گزاره شرطی هستند كه مقدم و تالی آنها گزارههای انفرادی با حد موضوع يكسان است. از جمله موردهای جانشینی تابع گزارهای
(x)(Hx ⊃ Mx)
گزاره های شرطی:
Ha⊃Ma, Hb⊃Mb, Hc⊃Mc, Hd⊃Md
و مانند آنها هستند.
همچنين توابع گزارهای وجود دارد كه موردهای جانشینی آنها عبارت از عطف گزارههای انفرادی با حد موضوعی یکسان است. بنابراین
Ha•Ma, Hb•Mb, Hb•Mb, Hb•Mb
و مانند آنها موردهای جانشین تابع گزارهای Hx•Mx هستند.
همچنين تابع گزارهای Hx ∨ Mx وجود دارد كه موردهای جانشین آن تركيب فصلی Ha∨Ma و Hb∨Mb و مانند آنها است.
در واقع گزاره مرکب تابع–ارزشی، كه گزارههای مؤلفه ای ساده آن گزارههای انفرادی با حد موضوع يكسان هستند، را میتوان بعنوان مورد جانشینی یک تابع گزارهای درنظر گرفت كه شامل بعضی يا همه رابطهای تابع-ارزش مانند ~، •، ≡، ⊂، ∨ و به علاوه محمولهای ..., Ax, Bx, Cx, Dx باشد. در برگردان گزاره A به
(x)(Hx ⊃ Mx)
پرانتزها نشان گذاری نگارشی هستند. آنها دال بر اين هستند كه سور کلی (x) "كارزده به" يا "دارنده در دامنه خود" همه (مجتمع) تابع گزارهای Hx⊃Mx است.
قبل از آنكه به سراغ بحث درباره صورتهای سنتی گزارههای حملی برويم بايد گفت كه فرمول نمادين ما (x)(Hx⊃Mx) نهتنها برگردان گزاره استاندارد ساخت «همه M H است»، بلكه برگردان هر جمله ديگر فارسی كه دارای معنای يكسان است نيز هست. فهرستی جزئی از آنها را میتوان اينگونه نوشت (H را ب و M را ج میگیریم):
«يك ب يك ج است»،
«هر بای ج است»،
«هر ب ج است»،
«هيچ ب غیرج نيست»،
«اينگونه نيست كه «بای ج نباشد»،
«هرچيز كه ب است ج هم است»،
«اگر چيزی ب است آن چيز ج است»،
«هرچه است ب ج هم هست»،
«فقط چيزی كه ج است ب است»،
«هيچ چيز مگر ج ب نیست»
و «چيزی نيست كه ب باشد ولی ج نباشد».
در بعضی عبارات فارسی كه حد زمانی بكاربرده میشود، قصد از آن ارجاع به زمان نيست و میتوانند گمراه كننده باشند. بنابراين گزاره «بها هميشه ج هستند» بطور معمول معنی روشن «همه بها ج هستند» را دارد. همينطور یک معنی يكسان میتواند با كاربرد اسامی مجرد بيانشود: «انسانيت مستلزم فناپذيری است» كه بطور صحيح به عنوان يك گزاره A برگردان میشود. میتوان اين را كه زبان منطق نمادين دارای يك عبارت تك برای تعداد قابل ملاحظهای جمله فارسی است را يك امتياز از جهت مقاصد گزارشورزی و شناختی به حساب آورد ــ گرچه قطعاً يك نقص از نقطهنظر صناعت كلام و بيان شاعرانه است.
| سور گذاری گزاره A |
گزاره A «همه انسانها فانی هستند» میگوید، اگر چيزی یک انسان است آنگاه آن فانی است. بعبارت ديگر، برای هر شئ دادهشده x، اگر x يك انسان است آنگاه x فانی است. با جانشینی نماد نعل اسبی(⊂) برای «اگر – آنگاه» خواهيم داشت: ,برای هر x طبق نمادسازی برای توابع گزارهای و سورها عبارت بالا بصورت زير نوشته میشود: (x)(Hx ⊃ Mx)
|
| سور گذاری گزاره E |
گزاره E «هيچ انسان فانی نيست» میگوید، اگر چيزی انسان است آنگاه آن فانی نيست. بعبارت ديگر، برای هر شئ دادهشده x، اگر x يك انسان است آنگاه x فانی نيست. با جانشینی نماد نعل اسبی برای «اگر – آنگاه» خواهيم داشت:
طبق نمادسازی برای توابع گزارهای و سورها، عبارت بالا به صورت زير نوشته میشود: (x)(Hx ⊃ ~Mx) برگردان نمادین پیشین نهتنها صورت سنتی E را به فارسی بازگو میکند، بلکه روشهای گوناگون گفتن یک چیز یکسان همچون: Hهایی وجود ندارند که M باشند، نیز بازگو میکند.
|
| سور گذاری گزاره I |
گزاره I «بعض انسان فانی است» میگوید، حداقل یک چیز هست که انسان است و فانی است. بعبارت دیگر، حداقل یک x وجود دارد که x انسان است و x فانی است. با جانشینی نماد ترکیب عطفی خواهیم داشت؛ حداقل یک x وجود دارد، به قسمی که x انسان است • x فانی است : طبق نمادسازی برای توابع گزارهای و سورها عبارت بالا بصورت زير نوشته میشود: (x)(Hx • Mx)
|
| سور گذاری گزاره O |
گزاره O «بعض انسان فانی نیست» مدعی است، که حداقل یک شئ هست که انسان است و فانی نیست. بعبارت دیگر، حداقل یک x هست که x انسان است و x فانی نیست. با جانشینی نماد ترکیب عطفی خواهیم داشت؛ حداقل یک x وجود دارد، به قسمی که x انسان است • x فانی نیست : طبق نمادسازی برای توابع گزارهای و سورها عبارت بالا بصورت زير نوشته میشود: (∃x)(Hx • ~Mx)
|
وقتی حروف یونانی فی(Φ) و سای(Ψ) برای نمایش محمولات، هرچه که باشند، بکار روند آنگاه میتوان چهار گزاره عام سنتی موضوع – محمول را میتوان در یک آرایه مربع شکل مطابق شکل ۲ نشان داد.
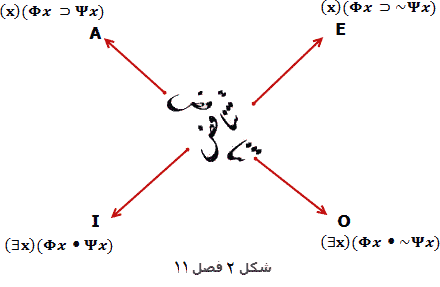
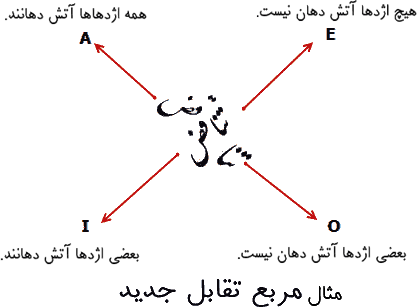
روابط نشان داده در نمودار ۲ در بالا با آنچه در نمودار ۶.۲ نشان داده شده مطابقت دارد. برای مثال، پیشتر دیدهایم که گزارههای A و O متناقض هستند، یعنی انکار یکدیگرند؛ و نیز دیدهایم که گزارههای E و I متناقض هستند
تا اینجا ما تحت این شرط ضعیف که حداقل یک شئ انفرادی وجود دارد کار کردیم. تحت این شرط ممکن است انتظار داشته یک گزاره I از گزاره نظیر خود A و یک گزاره O از گزاره نظیر خود E بدست میآید. اما در واقع، فرمول نگاری جدید ما از گزارههای حملی کلی بعنوان شرطی به تمامی تعبیر بولی را در بر دارد. برای نمونه، گزاره A میتواند خیلی هم خوب درست باشد و حال آنکه گزاره نظیر آن I نادرست باشد.
وقتی Φx یک تابع گزارهای است که موارد جانشین درست ندارد، آنگاه اهمیتی ندارد که تابع گزارهای Ψx چه قسم از موردهای جانشینی میتواند داشته باشد و در این صورت تسویر عمومی تابع گزارهای(مرکب) Hx⊃Mx درست خواهد بود.
برای مثال فرض کنید Cx کوتاهشده تابع گزاره ای «x یک قنطورس است» باشد [centaurs موجود اساطیری یونانی.] از آنجاکه قنطورس وجود ندارد هر مورد جانشین Cx نادرست است یعنی Cc ,Cb ,Ca... همه نادرست هستند. بنابراین هر مورد جانشین تابع گزارهای مرکب Cx⊃Bx یک عبارت گزارهای است که مقدم آن نادرست است. بنابراین موردهای جانشینی Cc⊃Bc ,Cb⊃Bb ,Ca⊃Ba, ...، همه درست هستند، زیرا هر عبارتگزارهای شرطی که تصدیق یک استلزام مادی است، چنانچه مقدم آن نادرست است باید درست باشد. و چون همه موردهای-جانشینی آن درست هستند، بنابراین سور عمومی تابع گزارهای Cx⊃Bx، که یک گزاره A، یعنی:
(x)(Cx ⊃ Bx)
است درست خواهد بود. اما گزاره I نظیر آن یعنی:
(∃x)(Cx • Bx)
نادرست است، زیرا تابع گزارهای Cx•Bx دارای مورد جانشین درست نیست. اینکه Cx•Bx مورد جانشین درست ندارد حاصل این واقعیت استکه Cx مورد جانشین درست ندارد. موارد جانشین گوناگون Cx•Bx عبارتند از: Cc•Bc, Cb•Bb, Ca•Ba .... که همه آنها گزاره عطفی با مولفه اول نادرست هستند، زیر Cc ,Cb ,Ca... همگی نادرست هستند. چون همه موارد جانشینی آن نادرست هستند، پس سور وجودی تابع گزارهای Cx•Bx که گزاره I یعنی:
(∃x)(Cx • Bx)
است نادرست خواهدبود. بنابراین یک گزاره A ممکن است درست باشد، حالآنکه گزاره نظیر I آن نادرست باشد.
این تحلیل نیز نشان میدهد که چرا ممکن است گزاره E درست باشد، حال آنکه گزاره نظیر آن O نادرست باشد. چنانچه در بحث قبل تابع گزارهای Bx را با تابع گزاره ای Bx~ تعویض کنیم آنگاه
(∃x)(Cx ⊃~Bx)
نادرست خواهد بود و البته روشن نیز است که قنطورسی وجود ندارد.
نکته اصلی مطلب این است که گزاره A و گزاره E مدعی نیستند یا مفروض نمیگیرند که شیئی وجود دارد؛ ادعای آنها این است که (اگر برای این، آنگاه برای بقیه آنها) نیز برقرار است. اما گزاره I و گزاره O مفروض میگیرند که اشیائی هست؛ آنها مدعی هستند که (این و دیگری) برقرار است. سور وجودی در گزارههای I و O موجب یک تفاوت بسیار عمده میشود؛ که خیلی راحت میتواند موجب شود از گزارهای که مدعی وجود شئ یا مفروض گرفتن آن نیست، وجود هر شیئی از آن نتیجه گرفته شود.
اگر این فرض عام که حداقل یک شئ انفرادی وجود دارد را مفروض بگیریم، آنگاه
(x)(Cx ⊃ Bx)
نتیجه میدهد:
(∃x)(Cx ⊃ Bx)
اما این گزاره آخری یک گزاره I نیست. گزاره «بعضی قنطورسها زیبایند» بصورت نمادین عبارت است از
(∃x)(Cx • Bx)
اما آنچه که بصورت:
(∃x)(Cx ⊃ Bx)
نمادین شدهاست، به زبان فارسی میتواند مطابق با «حداقل یک شئ وجود دارد، به قسمی که اگر آن یک قنطورس باشد آنگاه آن زیباست» برگردان شود. این نمیگوید که یک قنطورس وجود دارد، بلکه فقط میگوید یک شئ انفرادی هست که یا یک قنطورس نیست یا زیباست. این گزاره فقط در دو حالت نادرست است. یکم: اگر اصلاً شئ انفرادی وجود نداشته باشد و دوم: اگر همه اشیاء انفرادی قنطورس باشند و هیچ یک زیبا نباشند. حالت اول با تصریح این فرض (آشکارا درست)، که حداقل یک شئ انفرادی در جهان هست، منتفی میشود. حالت دوم یعنی هر گزاره به صورت
(∃x)(Cx ⊃ Bx)
در مقابل با گزاره معنیدار I
(∃)(Cx • Bx)
آنقدر نامحتمل است که به معنیدار نبودن گره میخورد.
آنچهکه گفتهشد باید روشن ساختهباشد که گرچه در زبان فارسی گزاره های I ,A «همه انسان فانی است» و «بعض انسان فانی است» فقط در واژههای آغازی خود «همه» و «بعض» متفاوتند، تفاوتشان در معنی صرفاً منحصر به حضور سور عمومی و وجودی نیست، بلکه ژرفتر از آن است. توابع گزارهای سوردار که گزارههای A و O را بدست دادهاند، فقط بطور متفاوت سوردار نشدهاند، آنها توابع گزارهای متفاوت هستند یکی شامل "⊃" و دیگری شامل «•» است. بعبارت دیگر، گزارههای A و I آنگونه که در زبان فارسی به نظر میرسند شبیه نیستند. تفاوت آنها در نمادین کردن توابع گزارهای و سوره به وضوح هویدا میشود.
اگر نماد نقیض (~) در فرمولهایی که بهقصد انجام اعمال منطقی در دست است وجود داشته باشد، چنانچه این نماد فقط به محمولات ساده کارزده باشد، آنگاه انجام اعمال سادهتر خواهند شد. اینکار را به آسانی میتوان انجام داد. بنابراین، میخواهیم به طریقی جایگزینی (تعویض) در فرمولها انجام دهیم، بهقسمیکه این نتیجه حاصل شود. این کار را میتوان بهآسانی انجام داد. از قاعده جایگزینی که در فصل 10 تاسیس شد میدانیم که همیشه مجاز هستیم یک عبارت را با عبارت منطقاً هم ارز دیگری تعویض کرد و برای اینکار چهار همارزی منطقی (فهرستشده در بالا) در دسترس است که در هرکدام از گزارهها نمایان است که سور نقضشده همارز با گزاره دیگری است که در آن نشان نقیض مستقیماً به محمول کارزده است. با کارزدن قواعد استنتاج، که دیگر آشنای قدیمی ما هستند، میتوان نشان نقیض را طوری جابجا کرد که در پایان، آنها دیگر به عبارتهای مرکب بکارزده نباشند و فقط به محمولات ساده کارزده باشند. برای مثال فرمول
~(∃x)(Fx • ~Gx)
میتواند درپیهم بازنویسی شود. اول، وقتی که همارزی منطقی سوم (فهرست شده در بالا) را بکار بندیم، فرمول به صورت زیر درخواهد آمد
(x)~(Fx • ~Gx)
سپس قضایای دمورگان را بکار میبندیم، که خواهد شد:
(x)(~Fx ∨ ~~Gx)
سپس کار زدن نقض دوگانه فرمول
(x)(~Fx ∨ Gx)
را برای ما حاصل میکند.
و سرانجام با فراخوان تعریف استلزام مادی فرمول اصلی به گزاره A
(x)(Fx ⊃ Gx)
بازنویسی میشود.
به یک فرمول که در آن نشان نقیض فقط به محمولات ساده بکار زده باشد، یک فرمول صورت–نرمال میگویند.
قبل از اینکه به مبحث استنتاجهای گزارههای غیرمرکب وارد شویم، خواننده باید تا اندازهای، در عمل، به ترجمه از فارسی به نمادگذاری منطقی ما مهارت کسب کردهباشد. زبان فارسی و کلاً زبانهای طبیعی، آنچنان دارای سازههای اصطلاحی و بیقاعده هستند که قواعد سرراستی برای برگردان جملهای از آن به نمادگذاری منطقی وجود ندارد. آنچه در هرحالت مورد نیاز است معنی جمله است، که باید فهمیدهشود و سپس برحسب توابع گزارهای و سورها بیان شود.
الف: هریک از موردهای زیر را به توابع گزارهای و سورها ترجمه کنید، در هر مورد کوتهسازی پیشنهادی را بکار ببندید و فرمولها را طوری درآورید که با سور شروع شوند و نه با نماد نقیض.
مثال: ۱- هیچ انسان بیرحم بدون اندازهای حس همدردی نیست. (x:Bx یک بیرحم است؛ x:Px تااندازهای حس همدری دارد.)
حل:
(x)(Bx⊃Px)
۲-گنجشکها پستاندار نیستند (x:Sx گنجشک است، x:Mx پستاندار است).
۳- خبرنگاران حاضرند (x:Rx یک خبرنگار است؛ x:Px حاضر است).
۴-پ رستارها همیشه ملاحظه کارند. (x:Nx پرستار است؛ x:Cx ملاحظه کار است).
۵*- سیاستمداران همیشه ثروتمند نیستند. (x:Rx سیاستمدار است؛ x:Rx ثروتمند است).
۶- شناکردن پنگوئن بودن است. (Sx شناگری؛ x:Px یک پنگوئن است).
۷- هیچ پیشاهنگی هرگز تقلب نمی کند (x:Bx پیشاهنگ ا ست؛ x:Cx تقلب می کند).
۸- فقط پزشکان مجوزدار میتوانند برای معالجات پزشکی پول دریافت کنند. (x:Lx یک پزشک مجوزدار است؛ x:Cx می تواند معالجات پزشکی پول دریافت کند).
۹-نیش مار بعضی وقتها کشنده است. (x:Sx یک نیش مار است؛ x:Fx کشنده است).
۱۰*- سرماخوردگی معمولی هرگز کشنده نیست. (x:Cx یک سرماخوردگی معمولی است؛ x:Fx کشنده است). 11-یک کودک انگشتش را به سمت امپراطور نشانه کرده است. (x:Cx کودک است؛ x:Px انگشتش را به سمت امپراطور نشانه کرده است).
۱۱- چنین نیست که هر کودکی انگشتش را به سمت امپراطور اشاره کرده باشد. (x:Cx یک کودک است؛ x:Px انگشتش را به سمت امپراطور اشاره کرده است).
۱۲- همه درخشان ها طلا نیستند. (x:Jx درخشان است؛ x:Ix طلا است).
۱۳- هیچکس مگر شجاعان شایسته انصاف هستند.
(x:Bx شجاع است؛ x:Dx شایسته انصاف است).
۱۵*- فقط شهروندان آمریکا میتوانند در آمریکا رأی دهند. (x:Cx یک شهروند آمریکا است؛ x:Vx می تواند در انتخابات آمریکا رأی دهد).
۱۶- شهروندان آمریکا میتوانند فقط در انتخابات آمریکا رای دهند. (x:Ex انتخاباتی است که شهروندان آمریکا میتوانند رای بدهند؛ x:Ux یک انتخابات آمریکا است).
۱۷- چنین نیست که همه متقاضیها استخدام شده باشند. (x:Jx متقاضی ا ست؛ x:Hx استخدام شده است).
۱۸- چنین نیست که هر متقاضیای استخدام شده باشند. (x:Jx متقاضی ا ست؛ x:Hx استخدام شده است).
۱۹- هیچ چیز مهمی گفته نشد. (x:Lx مهم است؛ x:Sx گفته شد).
۲۰*- کسانی حق به شهروندان دارند کسانیاند که دل کمک کردن دارند. (x:Cx حق شهروند شدن دارد؛ x:Hx دل کمک کردن دارد).
حل ستاره دارها
5- (∃x)(Dx•~Rx) 10- (x)(Cx⊃~Fx) 15- (x)(Vx⊃Cx) 20- (x)(Cx≡Hx)
ب: هریک از موردهای زیر را به توابع گزارهای و سورها ترجمه کنید، در هر مورد فرمولها را طوری درآورید که با سور شروع شوند و نه با نماد نقیض.
۱- هیچ از جنگ بدست نمیاید مگر با حسابگری ــناپلئون بناپارت
۲- هیچکس عقیده به قانون طبیعت ندارد. ــ
۳- او که هستی و آزادی خویش را میجوید، کسی است که هر روز از نو فتحی در پیش دارد.
۴- هیچ بشری بدبخت نیست مگر محکوم به زندگی در ایرلند باشد.
۵*- چنین نیست که هر چیز سالم خوب باشد و چنین نیز نیست که هر چیز خطرناک بد باشد.
۷- یک مساله خوب بیانشده مسالهای نیم حلشده است.
۸- یک جادوگر یا ساحره تک نیست که به غلط رفته باشد و او در اسلایترین/Slytherin نبوده باشد.ــ
۹- هرکس چیزی را دوست ندارد، اما همه ویلی نلسون را دوست ندارند.
*۱۰-هیچ کس مگر یک کله سنک همیشه بجز برای پول نوشت.
حل ستاره دارها
۱. [(∃x)(Gx•~Sx)]•[(∃x)(Dx•~Bx)]
۱۰. (x)(~Bx⊃~Wx)
ج) برای هر یک ار فرمولهای زیر فرمول صورت-نرمال منطقاً همارز با آن را بیابید.
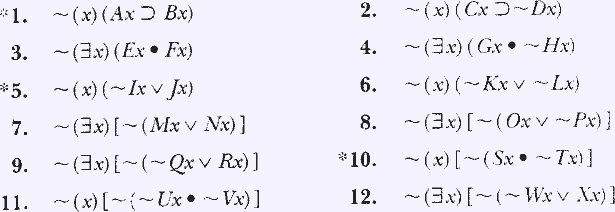
حل ستاره دارها
۱. (∃x)(Ax•~Bx) ۶. (∃x)(Ix•~Jx) ۱۰. (∃x)(Sx•~Tx)
■ ■ ■ ■ ■

 (∃x)(
(∃x)(