آزمون اعتبار استدلال با استفاده از جداول ارزش: روش جدول ارزش کامل

اکنون با دانستن دقیق معنی اعتبار یابی‌اعتباریِ یک استدلال، می‌توان روشی برای آزمون هر استدلال تابع-ارزش بدست داد. روش ما استفاده از جدول ارزش است که در عین سادگی بسیار توانا هم هست. این روش صرفاً استفاده از  تحلیل صورت‌های استدلالی است که تاکنون دیده‌ایم.

برای آزمون یک صورت استدلالی، همه موارد جانشین صورت استدلال را بررسی خواهیم کرد تا ببینیم آیا می‌توان حالتی یافت که در آن مقدمات درست ولی نتیجه نادرست باشد. گرچه یک صورت استدلال به تعداد نامحدود مورد جانشینی دارد، ولی نیاز نیست تا آن‌ها را یک‌به‌یک بررسی نماییم. ازآنجاکه مرکز توجه ما درستی یا نادرستی مقدمات و نتیجه آن‌هاست، فقط باید مقادیر ارزش درگیر را بررسی کنیم. استدلال‌هایی که ما در اینجا با آن‌ها کارداریم، فقط شامل گزاره‌ها ساده و گزاره‌های مرکبی هستند که از گزاره‌های ساده و توسط رابط‌های تابع ارزش، که با نمادهای ⋁، ⊂، • و ~ نمادین شده‌، ساخته‌شده‌اند (یعنی استدلال‌های تابع-ارزش.)

وقتی صورت استدلال فقط دارای دو متغیر گزاره‌ای p و q است،همه موارد جانشین آن‌ها به قرار:

جانشینی گزاره درست برای p و هم برای q است، یا
جانشینی گزاره درست برای p و نادرست برای q است، یا
جانشینی گزاره نادرست برای p و درست برای q است، یا
جانشینی گزاره نادرست برای p و هم برای q ،

است.

همه این حالات مختلف را می‌توان به راحت‌ترین وجه در یک جدول ارزش سرجمع کرد. برای آزمون اعتبار صورت استدلال:

(P_۱): p ⊃ q
(P_۲): q
∴ p 

جدول ارزش زیر را تشکیل می‌دهیم:

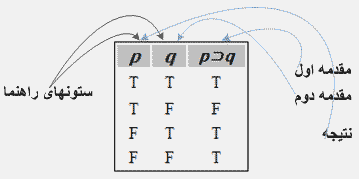
هر سطر این جدول یک دسته کامل از مورد‌های جانشینی را نشان می‌دهد. T و F در دو ستون اول به‌عنوان راهنما نشان‌دهنده مقادیر ارزش گزاره‌های جایگزین‌شده برای متغیرهای  p و q در صورت استدلال هستند.  عنوان سومین ستون "مقدمه"  اول  و ستون دوم  "مقدمه" دوم و ستون اول "نتیجه" صورت استدلال است. در بررسی این جدول ارزش درمی‌یابیم در سطر سوم برای هر دو مقدمه T و برای نتیجه F وجود دارد؛ این نشان می‌دهد حداقل در یک مورد جانشینی، این استدلال دارای مقدمات درست و نتیجه نادرست است. وجود این سطر برای نشان دادن بی‌اعتباری این استدلال کفایت می‌کند. به هر استدلالی به این صورت (یعنی، هر استدلال که صورت نوعی آن صورت استدلال داده‌شده است) گفته مرتکب مغالطه وضع تالی گردیده، زیرا مقدمه دوم وضع تالی (تصدیق تالی) گزاره شرطی در مقدمه اول است. ➥

جدول ارزش گرچه در مفهوم ساده ولی ابزاری توانمند است. تشکیل جدول ارزش، به‌گونه صحیح، برای استفاده در تثبیت اعتبار یا بی‌اعتباری هر صورت استدلال دارای اهمیت اساسی است. برای تشکیل صحیح جدول ارزش باید برای هر متغیر گزاره‌ای مانند r ،q ،p و مانند آن‌ها، که در صورت استدلال حضور دارند، ستون‌های راهنما وجود داشته باشند. این جدول باید همه ترکیبات ممکنه درستی و نادرستی متغیرهای گزاره‌ای را نمایان سازد، بنابراین باید تعدادی سطر نیز وجود داشته باشند که برای درستی و نادرستی این متغیرهای کافی باشند، از قرار ۴ سطر وقتی دو متغیر وجود دارد و ۸ سطر وقتی سه متغیر وجود دارد. بطور کلی، یک صورت استدلال دارای n متغیر گزاره‌ای نیاز به جدول ارزشی با n ستون راهنما و ۲ⁿ سطر دارد. بعلاوه، باید ستون‌های اضافی برای مقدمات و نتیجه در نظر گرفت و همچنین یک ستون به ازای هر عبارت نمادین که مقدمات و نتیجه از آن‌ها ساخته‌شده‌اند. ساختن جدول ارزش به این شیوه که گفته شد در اصل انجام یک کار به روش مکانیکی است و نیاز به‌دقت در شمارش و جایگذاری T و F در ستون‌های بجا دارد.

همه آنچه گفته شد، توسط فهم ما از رابط‌های تابع-ارزش یعنی ⋁، ⊂، • و ~ سرچشمه می‌گیرند، یعنی تحت آن حالاتی که یک گزاره مرکب تابع-ارزش درست یا نادرست می‌شود.

وقتی جدول ساخته شد و با سطرهای کامل شده در مقابل قرار گرفت، آنگاه باید آن را به‌طور صحیح خواند، یعنی، آن را برای ارزیابی صورت استدلال به‌طور صحیح بکار گرفت. باید دقت کرد که کدام ستون‌ها نماینده مقدمات صورت استدلال مورد آزمون هستند و کدام ستون نتیجه استدلال را نمایندگی می‌کند.

در آزمون استدلال بالا که آن را بی‌اعتبار برآورد کردیم، ابتدا توجه کردیم که ستون دوم و ستون سوم در جدول ارزش نمایانگر مقدمه دوم (نشان‌گذاری شده با P_۲) و مقدمه اول (نشان‌گذاری شده با P_۱) در صورت استدلال هستند و بعلاوه، نتیجه استدلال توسط اولین ستون (نشان‌گذاری شده با ∴) نمایندگی شده. با توجه به صورت استدلال موردارزیابی و ترتیبی که ستون‌ها در جدول ساخته‌شده قرار دارند، ممکن است مقدمات و نتیجه به هر ترتیبی در بالای جدول ظاهر شوند. حضور آن‌ها در چپ یا راست جدول دارای اهمیت نیست، وقتی آن‌را بکار می‌بریم باید بدانیم چه ستونی چه چیزی را نشان می‌دهد و همچنین باید بدانیم که به دنبال چه چیزی هستیم. از خود می‌پرسیم آیا حالتی وجود دارد که در سطری از آن، همه مقدمات درست و نتیجه نادرست است؟ اگر چنین سطری وجود دارد، استدلال نامعتبر است، اگر چنین سطری وجود ندارد استدلال معتبر است. پس‌ازآنکه همه‌ی سطرها بادقت و آشکاری پیشِ‌روی قرارگرفت، آنگاه داشتن دقت زیاد در خواندن جدول داری بیشترین اهمیت است.

■ رشد تصاعدی جدول ارزش

همانطور که در بالا گفته‌شد بطورکلی، یک صورت استدلال دارای n متغیر گزاره‌ای نیاز به جدول ارزشی با n ستون راهنما و ۲ⁿ سطر دارد. برای مثال صورت استدلال (آ) در زیر

(P_۱): p ⊃ q
(P_۲): q ⊃ ~r
∴ p ⊃ ~r

دارای سه متغیر گزاره‌ای q ،p و r است و بنابراین باید جدول ارزشی با ۳ ستون راهنما (برای q ،p و r به ترتیب الفبایی) و ۲^۳ یا ۸ سطر باشد.

قرارداد استاندارد و پذیرفته در اینجا برای اطمینان از اینکه همه ترکیبات مقادیر ارزش در جدول ارزش نشان داده شده است، برای ۳ متغیر گزاره‌ای به قرار زیر است.

• زیرِ متغیر گزاره‌ای سوم و در ستون راهنمای سوم (یعنی r) به ترتیب و یک درمیان T و F را قرار دهید.
• زیرِ متغیر گزاره‌ای دوم و در ستون راهنمای وسط (یعنی q) به ترتیب و یک درمیان دو T و دو F را قرار دهید.
• زیرِ متغیر گزاره‌ای یکم و در ستون راهنمای یکم (یعنی p) به ترتیب و یک درمیان چهار T و چهار F را قرار دهید.

اگر در صورت استدلال چهار متغیر گزاره‌ای r ،q ،p و s وجود داشته باشد، از ستون راهنمای چهارم زیر s آغاز کنید و یک درمیان مطابق T و F را قرار دهید. چهار ستون راهنما برای این چهار متغیر گزاره‌ای به‌قرار زیر است.

بنابراین، برای پنج متغیر گزاره‌ای s، r ،q ،p و t اولین ستون از جدول ارزش ۳۲ ستونی (برای p) دارای شانزده T و در دنبال آن شانزده F خواهد بود. ستون دوم (برای q) دارای هشت T، هشت F، هشت T و هشت F خواهد بود و همینطور تا آخرین ستون راهنما.

همانطور که در بالا آمد، یک جدول ارزش باید دارای یک ستون عمودی برای هر یک از مقدمات و نتیجه و نیز یک ستون برای هر گزاره مؤلفه‌ای باشد که مقدمات و نتیجه از آن‌ها تشکیل شده است. بنابراین، صورت استدلال بالا، یعنی

(P_۱): p ⊃ q
(P_۲): q ⊃ ~r
∴ p ⊃ ~r

باید دو ستون اضافی برای دو مقدمه در سمت راست سه ستون راهنما داشته‌باشد. همچنین یک ستون بلافاصله در سمت راست ستونِ راهنمای سوم برای ~r و یک ستون در انتهای سمت راست برای نتیجه وجود داشته باشد. حاصل این‌کار، چهارچوبه کامل‌نشده جدول-ارزش را بدست می‌دهد، که شامل هفت ستون و هشت سطر شماره گذاری‌شده برای مقادیر ارزش (یعنی T و F) است. بسیار مهم است که در این مرحله، مقدمات و نتیجه بدرستی برچسب گذاری شوند تا اطمینان حاصل شود بعداً، یعنی وقتی جدول ارزش را تکمیل کردیم، مقادیر ارزش را فقط در ستون‌های مقدمات و نتیجه بررسی کنیم.

به‌طورکلی، ستون‌های مؤلفه‌های مرکب در مقدمات و نتیجه را قبل از ساختن ستون‌های مقدمات و نتیجه به ترتیب درجه ترکیب آنها از ساده‌ترین تا مرکب‌ترین، می‌سازیم. برای مثال، برای صورت گزاره‌ای:

[p ⋁ q) • r] ⊃ s

ابتدا یک ستون برای مؤلفه‌ی زیر می‌سازیم

p ⋁ q

سپس یک ستون برای مؤلفه‌ی زیر می‌سازیم

(p ⋁ q) • r

سرانجام یک ستون برای مؤلفه‌ی زیر می‌سازیم.

[p ⋁ q) • r] ⊃ s

با در نظرگرفتن چهارچوبه جدول-ارزش در بالا، اکنون ساختن آن را به‌طور مکانیکی با نوشتن T و F برای هر صورت مؤلفه‌ای تابع-ارزش با شروع از ~r آغاز می‌کنیم. برای هر مورد نیاز است تا تعریف عملگر منطقی (رابط منطقی) اصلی صورت گزاره‌ای را مطابق جدول-ارزش بدانیم. صورت گزاره‌ای ~r وقتی درست است که r نادرست باشد و وقتی نادرست است که r درست باشد. با نگاه به ستون r ستون ~r را می‌سازیم که حاصل آن ستون کامل‌شده‌ی ~r مطابق زیر خواهد بود.

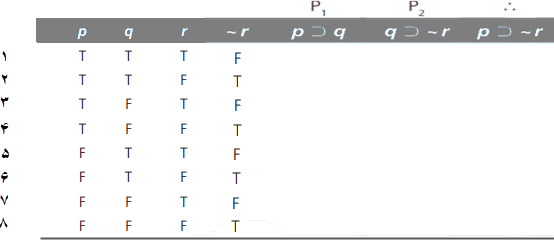
در قدم بعد، ستون مقادیر ارزش را برای مقدمه ۱، یعنی p⊃q کامل می‌کنیم. این یک صورت گزاره‌ای شرطی است و می‌دانیم که یک شرطی فقط وقتی نادرست است که مقدم آن درست و تالی آن نادرست باشد. بنابراین، با نگاه به ستون‌های‌ مقدم، یعنی p، و تالی، یعنی q، یک T زیر p⊃q، مگراینکه p درست و q نادرست باشد، می‌نوسیم. بنابراین و ازآنجاکه، فقط در سطرهای ۳ و ۴ است که p درست و q نادرست است، F را در آن سطرها و T را در سطرهای ۱، ۲ و ۵ تا ۸ می‌نویسیم.

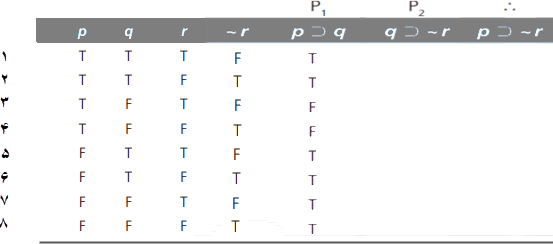
قدم بعدی پرکردن ستون مقادیر ارزش برای مقدمه ۲، یعنی q⊃~r است. این مقدمه نیز یک گزاره شرطی است و فقط وقتی نادرست است که مقدم آن، یعنی q، درست و تالی آن، یعنی ~r، نادرست باشد. بنابراین برای پرکردن صحیح این ستون با T و F به ستون q و ستون ~r نگاه می‌کنیم. فقط در سطرهای ۱ و ۵ است که q درست و ~r نادرست است، بنابراین q⊃~r بجز در سطرهای ۱ و ۵ درست خواهد بود.

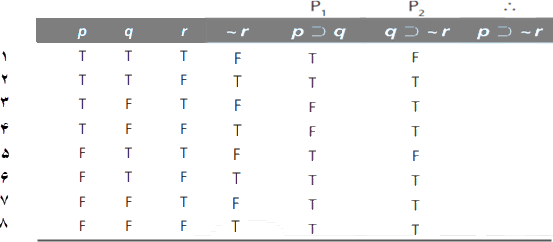
اکنون وقت پرکردن ستون مقادیر ارزش برای نتیجه، یعنی p⊃~r، است. این نیز یک گزاره شرطی است که فقط وقتی نادرست است که مقدم آن ،یعنی p، درست و تالی آن، یعنی ~r، نادرست باشد. فقط در سطرهای ۱ و ۳ است که p درست و ~r نادرست است، بنابراین p⊃~r بجز در سطرهای ۱ و ۳ درست خواهد بود.

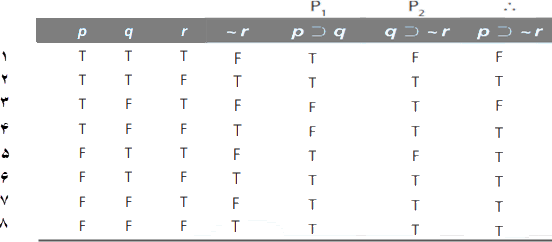
اکنون جدول ارزش استدلال کامل شده است. وقتی جدولِ ساخته‌شده و کامل‌شده در مقابل است، ضرورت دارد تا آن را به‌طور صحیح خواند — یعنی، آن را برای ارزیابی صورت استدلال موردنظر به‌کارزد. برای این منظور، حیاتی است که مقدمات و نتیجه را همان‌طور که در بالا گفته شد برچسب‌گذاری کنیم. این کمک می‌کند تا اطمینان یابیم که فقط به ستون‌هایی نگاه کنیم که مقدمات و نتیجه در آن‌ها در تعیین اعتبار یا بی‌اعتباری صورت استدلال دخیل هستند.

در آزمون اعتبار این استدلال، پرسش ما مثل همیشه این است که: آیا ممکن است در این صورتِ استدلال همه مقدمات درست و نتیجه نادرست باشد؟ اگر در این صورتِ استدلال ممکن باشد همه مقدمات درست و نتیجه نادرست باشد — یعنی، اگر این صورتِ استدلال نامعتبر باشد — آنگاه برای حداقل یک ترکیب از مقادیر ارزش برای متغیرهای گزاره‌ای، دارای تمام مقدمات درست و یک نتیجه نادرست است، که این حداقل در یک سطر از جدول ارزش کامل‌شده به نمایش در خواهد آمد.

از طرف دیگر، اگر این صورت استدلال نتواند همه مقدمات درست و یک نتیجه نادرست داشته باشد — یعنی، اگر این صورت استدلال معتبر باشد — برای هر ترکیب از مقادیر ارزش برای متغیرهای گزاره‌ای خود نمی‌تواند همه مقدمات درست و یک نتیجه نادرست را در جدول ارزش کامل‌شده داشته باشد.

بنابراین، برای تعیین اینکه آیا حداقل یک مورد از چنین حالتی وجود دارد یا نه➥، فقط باید هر سطر را به‌صورت مکانیکی اما با دقت وارسی کنیم تا ببینیم آیا در سطری، همه مقدمات درست و نتیجه نادرست است. در ردیف اول، می‌بینیم مقدمه ۱ درست است، اما مقدمه ۲ نادرست است. در خط ۲، هر دو مقدمه درست است، اما نتیجه نیز درست است، بنابراین ما به وارسی جدول به سمت پایین ادامه می‌دهیم. دیده می‌شود که هر دو مقدمه در سطرهای ۶، ۷ و ۸ درست هستند، اما در هر سه حالت نتیجه نیز درست است. وارسی دقیق نشان می‌دهد در هیچ چنین موردی، برای هیچ ترکیب از هشت ترکیب مقادیر ارزش برای متغیرهای گزاره‌ای، چنین نیست که هر دو مقدمه درست و نتیجه نادرست  باشد. این بدان معناست که صورت استدلال معتبر است.

به یاد داشته وقتی جدول ارزش کاملاً ساخته شد، پرسش این است: آیا حالتی، یعنی تک سطری وجود دارد که در آن همه مقدمات درست و نتیجه نادرست باشد؟ اگر چنین سطری وجود دارد، آنگاه صورت استدلال نامعتبر است. اگر چنین سطری وجود ندارد صورت استدلال معتبر است. برای کارآمدی بیشتر می‌توان فقط به سطرهایی نگاه کرد که در آن‌ها نتیجه نادرست است. اگر در جدول ارزش بالا فقط به سطرهایی نگاه کنیم که نتیجه نادرست است، خواهیم دید که فقط در سطرهای ۱ و ۳ نتیجه درست است و در این هر دو حالت هر دو مقدمه باهم درست نیستند.

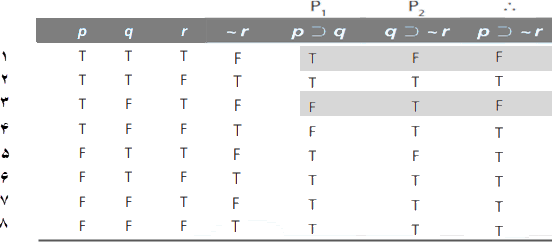
این به‌طور بسیار کارآمد به ما می‌گوید که این صورت استدلال معتبر است. (در قسمت ۱۰.۱۲، خواهیم‌دید که تکنیک جدول-ارزش کوتاهتر، از این روش کارآمدتر استفاده می‌کند و تنها حالت‌هایی را تولید می‌کند که نتیجه در آن‌ها نادرست است.)

صورت استدلالی زیر را ببینید.

(P_۱): p ⊃ q
(P_۲): q ⊃ r
(P_۳): ~r 
∴ p • ~q

ازآنجاکه، این صورت استدلال از سه متغیر گزاره‌ای تشکیل شده است، جدول-ارزش آن دارای سه ستون راهنما و هشت سطر، افزون براین یک ستون اضافی برای ~r، سه ستون اضافی برای مقدمات و یک ستون اضافی دیگر برای نتیجه خواهد بود. ما اکنون چهارچوبه جدول-ارزش را با هشت ستون و هشت سطر شماره گذاری‌شده به شرح زیر تشکیل می‌دهیم و دقت داریم که همه مقدمات و نیز نتیجه را برچسب گذاری کنیم.

در قدم بعد، با کاربرد دانش خود از گزاره‌های نقضی، شرطی و عطفی جدول ارزش را کامل می‌کنیم.

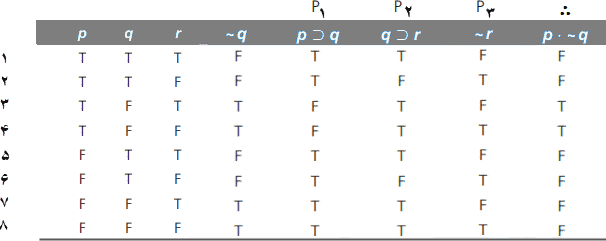
وقتی جدول ارزش به‌تمامی ساخته شد، می‌پرسیم: آیا حالتی در تک سطری وجود دارد که در آن همه‌ی مقدمات درست و نتیجه نادرست باشد؟ اگر چنین سطری وجود دارد، این صورت استدلال نامعتبر است. اگر چنین سطری وجود ندارد، این صورت استدلال معتبر است. با جستجوی نتیجه‌های نادرست، درمی‌یابیم که در این صورت استدلال، نتیجه برای همه حالت‌ها بجز دو مورد نادرست است. در چنین حالتی گاهی آسان‌تر و سریع‌تر خواهد بود، اگر در پی سطرهایی باشیم که همه مقدمات در آن‌ها دررست است. فقط یک سطر از این قسم وجود دارد.

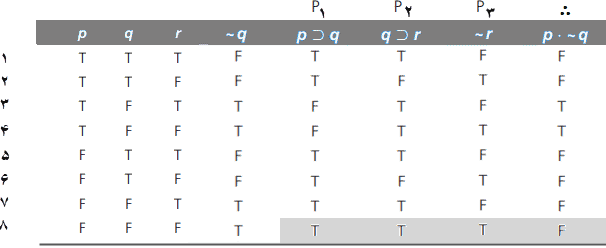
در این تک حالت، یعنی وقتی که همه مقدمات درست هستند، نتیجه نادرست است. آشکارا، این صورت استدلال می‌تواند دارای همه مقدمات درست و نتیجه نادرست باشد، زیرا وقتی p ،q و r همه نادرست باشند، مقدمات همه درست است، اما نتیجه نادرست است. جدول ارزش، هنگامی که به‌درستی ساخته شود و به‌درستی خوانده شود، به روشنی نشان می‌دهد، این صورت استدلال نامعتبر است.

سرآخر، صورت استدلال زیر را ببینید.

(P_۱): p ⊃ (q • r)
(P_۲): (q ⋁ r) ⊃ s
∴ p ⊃ s

ازآنجاکه، این صورت استدلال دارای چهار متغیر گزاره‌ای — r ،q ،p و s — است، جدول ارزش آن دارای چهار ستون راهنما و شانزده سطر خواهد بود. چه تعداد ستون برای این جدول ارزش نیاز است؟ برای هر گزاره مرکب، شامل مؤلفه‌های تابع-ارزش، یک ستون برای هر مؤلفه تابع-ارزش ایجاد می‌کنیم. بنابراین، برای اولین مقدمه باید مقادیر ارزس را در همه حالت‌ها برای گزاره مؤلفه‌ای q•r، قبل از تعیین مقادیر ارزش برای کل گزاره شرطی p⊃(q•r)، معین کرد. برای مقدمه دوم باید مقادیر ارزس را در همه حالت‌ها برای گزاره مؤلفه‌ای q⋁r، قبل از تعیین مقادیر ارزش برای کل گزاره شرطی (q⋁r)⊃s)، معین کرد. بنابراین این جدول ارزش به نه ستون نیاز دارد: چهار ستون برای متغیرهای گزاره، دو ستون برای مؤلفه‌های تابع-ارزشی q•r و q⋁r، دو ستون برای مقدمات و یک ستون برای نتیجه.

چهارچوبه جدول ارزش این صورت استدلال، با نه ستون و ۱۶ سطر، و برچسب‌های مورد نیاز برای مقدمات و نتیجه، به قرار زیر ساخته می‌شود.

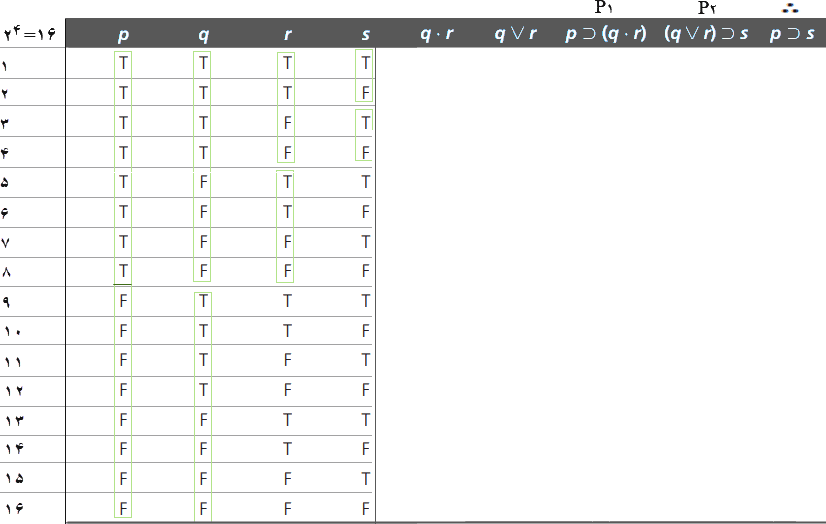
در قدم بعد، با کاربرد دانش خود از گزاره‌های عطفی و فصلی مقادیر T و F برای ستون ‌ q•rو سپس برای ستون q⋁r را وارد می‌کنیم.

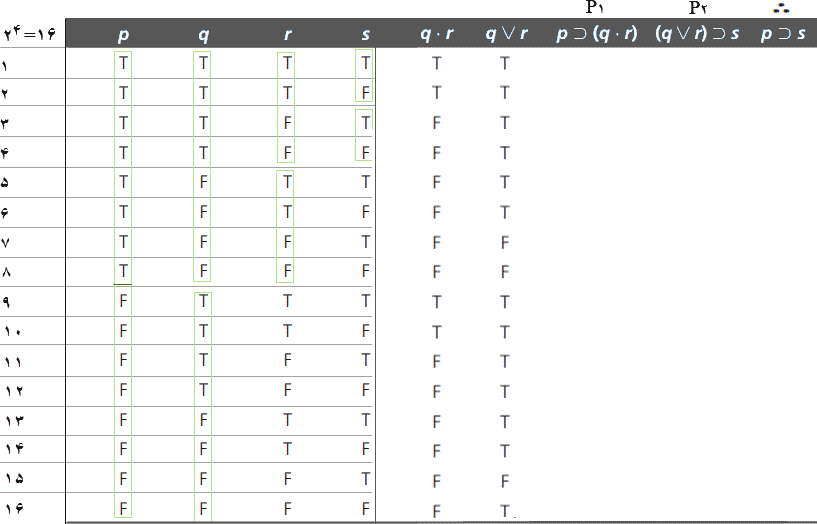
برای کامل کردن مقادیر ارزش برای ستون بعدی، ابتدا باید عمل‌گر (رابط منطقی) اصلی در مقدمه اول، یعنی p⊃(q•r)، را تعیین کرد. عمل‌گر اصلی بیرونی‌ترین عمل‌گر است — یعنی، آن عمل‌گر منطقی که بیرون از همه پرانتزها، کروشه‌ها و آکولادها است. در این حالت، مقدمه اول یک شرطی است زیرا بیرونی‌ترین عملگر منطقی آن "⊃" است. بنابراین، برای تعیین مقدار ارزش گزاره شرطی p⊃(q•r) در ستون هفتم، به مقدار ارزش مقدم آن، p در ستون اول، و مقدار ارزش تالی آن، (q•r) در ستون پنجم، برای هر ترکیب از مقادیر ارزش (یعنی در هر سطر) برای متغیرهای گزاره‌ای نگاه می‌کنیم. برای مثال، در خط ۳، هنگامی که q ،p و r به ترتیب درست، درست و نادرست هستند، مقدمه، p، درست است و نتیجه، (q•r)، نادرست است، بنابراین شرطی، p⊃(q•r)، نادرست است. به این ترتیب، T و F را در ستون هفتم برای p⊃(q•r) وارد می کنیم.

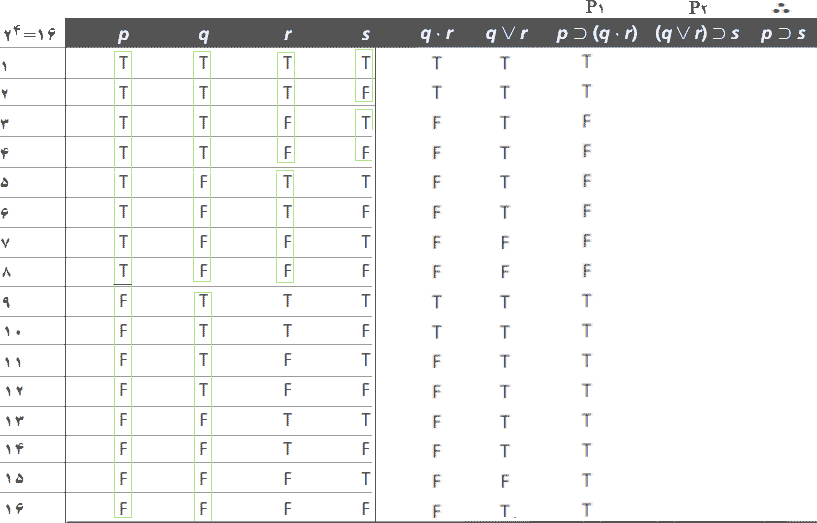
مقدمه دوم، (q⋁r)⊃s)، نیز یک شرطی است، زیرا عملگر منطقی اصلی (یا بیرونی‌ترین) "⊃" است. بنابراین، برای تعیین مقدار ارزش گزاره شرطی، (q⋁r)⊃s)، در ستون هشتم، به ارزش ارزش مقدم آن، q⋁r، در ستون ششم، و مقدار ارزش تالی آن، s، در ستون چهارم، برای هر ترکیب از مقادیر ارزش (یعنی در هر سطر) برای متغیرهای گزاره‌ای نگاه می‌کنیم. ببرای مثال، در خط ۱۲، وقتی r ،q و s به ترتیب درست، نادرست و نادرست هستند، مقدم، q⋁r، درست است و نتیجه، s، نادرست است، بنابراین شرطی، (q⋁r)⊃s)، نادرست است. به این ترتیب، T و F را در ستون ۸ برای (q⋁r)⊃s) وارد می‌کنیم.

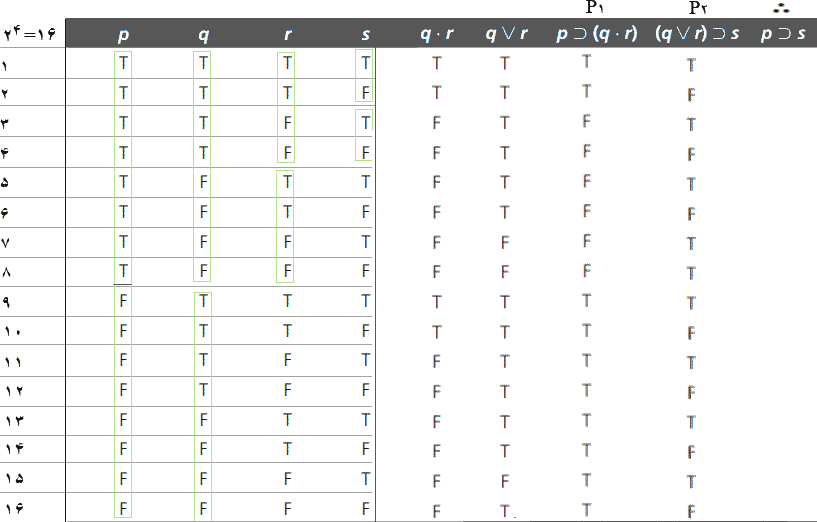
سرانجام، مقادیر ارزش برای نتیجه، یعنی p⊃s، را در ستون ۹ به‌عنوان یک تابع-ارزش از مقدار ارزش مقدم آن، یعنی p (در ستون اول)، و مقدار ارزش تالی آن، یعنی s (در ستون چهارم)، وارد می‌کنیم. جدول ارزش کامل‌شده به‌قرار زیر است.

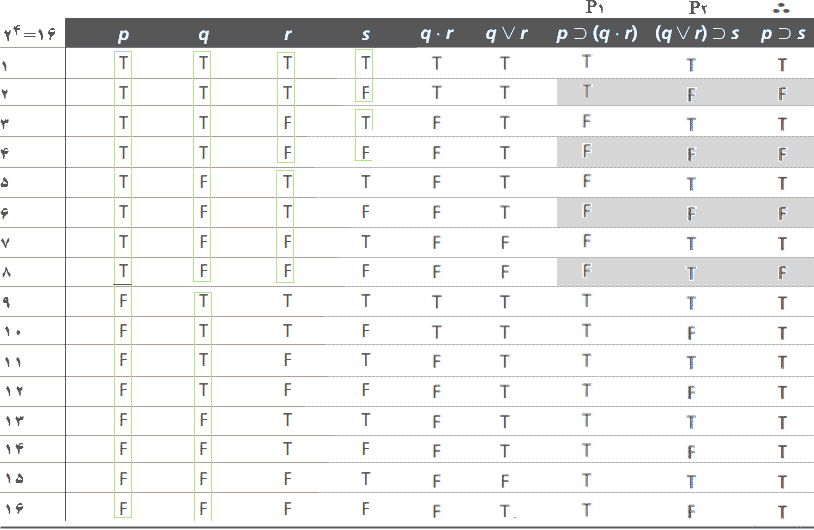
همانطور که در قسمت‌های سایه روشن مشخص شده، فقط چهار حالت وجود دارد که در آن نتیجه، p⊃s، نادرست است و در هر دو این حالت‌ها هر دو مقدمه درست نیستند. از آنجا که هیچ حالتی نیست که مقدمات آن همه درست و نتیجه نادرست باشد، این صورت استدلال معتبر است.

آنچه گفته‌شد نشان می‌دهد که روش جدول ارزش کامل برای آزمون صورت‌های استدلالی (و نیز استدلال‌ها) برای اعتبار، ساده، مکانیکی و بسیار توانمند است. با استفاده از این روش می‌توان هر صورت استدلال تابع-ارزش را اعتبارسنجی کرد.