برخی صورتهای رایج استدلال
منطق گزارهای و گزارههای تابع-ارزش
درآمد به منطق فصل ۹ قسمت ۷
در قسمت قبل روش جدول ارزش کامل (CTTM) را در منطق گزارهای همچون یک روند کارآمد (ولی نه کارساز) برای تعیین اعتبار یا بیاعتباری هر صورت استدلال (بهعبارت دیگر، تصمیم پذیری در منطق گزارهای) دیدیم. در این قسمت چهار صورت استدلالی معتبر بسیار رایج را به قرار قیاس فصلی، قیاس استثنائی، قیاس اقترانی و قیاس شرطی بعنوان صورتهای معتبر مقدماتی معرفی کردهایم.
۷.۹ برخی صورتهای رایج استدلال
آ. صورتهای رایج معتبر:
قیاس فصلی
قیاس گُسستار
Disjunctive Syllogism
یک صورت منطقی معتبر که در آن، یک مقدمه ترکیب فصلی است و مقدمه دیگر انکار یکی از دو فصل آن است و نتیجه درستی فصل دیگر است. این صورت با:
~p
∴q
قیاس استثنائی
قاعده وضع
قاعده تصدیق
Modus Ponence
Method of putting
Method of affirming
استدلالی که بر مبنای یک مقدمه شرطی و مقدمه دیگری که تائید مقدمِ مقدمه شرطی است، استوار باشد، و نتیجه نیز تالی مقدمه شرطی باشد.
این صورت با:
p
∴q
قیاس اقترانی
قاعده رفع
قاعده انکار
Modus Tollens
Method of taking away
Method of denying
استدلالی است که بر مبنای یک مقدمه شرطی و مقدمه دیگری که انکار تالیِ مقدمه شرطی است، استوار باشد، و نتیجه نیز انکار مقدمِ مقدمه شرطی باشد.
این صورت با:
~q
∴~p
قیاس شرطی
قیاس شرطی محض
Hypothetical Syllogism
Pure Hypothetical Syllogism
یک قیاس که شامل یک گزاره شرطی بهعنوان مقدمه است. اگر قیاس فقط شامل گزارههای شرطی باشد، قیاس شرطی "محض" نامیده میشود؛ اگر قیاس شامل یک مقدمه شرطی و یک مقدمه حملی باشد، قیاس شرطی "آمیخته" نامیده میشود.
این صورت با:
q ⊃ r
∴p ⊃ r
دو جهی ساختی
دو لمی ساختی
معضل سازنده
Constructive Dilemma
یک صورت استدلال معتبر ابتدایی شامل دو مقدمه و یک نتیجه. مقدمه اول ترکیب عطفی از دو گزاره شرطی است. مقدمه دوم یک ترکیب فصلی است که در آن فصل اول مقدم شرطی اول در مقدمه اول است و فصل دوم مقدم شرطی دوم در مقدمه اول است. نتیجه بطور معتبر اندریافت یک ترکیب فصلی است که در آن فصل اول تالی شرطی اول در مقدمه اول است و فصل دوم تالی شرطی دوم در مقدمه اول است.
برخی صورتهای استدلالی معتبر بسیار رایج و بطور شهودی قابلدرکاند. اکنون در موقعیتی هستیم تا آنها را بهطور دقیق مشخص کنیم، آنگونه که هر جا این صورتها بهکاربرده شدند، بتوان آنها را متمایز کرد. این صورتها نامهای خاص خود را، که بهطور گسترده نیز مورداستفاده قرار میگیرند، دارند و ما نیز از آنها با همین نامها یاد خواهیم کرد:
(۱) قیاس فصلی،
(۲) قیاس استثنائی،
(۳) قیاس اقترانی،
(۴) قیاس شرطی.
■ قیاس فصلی
یکی از سادهترین این صورتهای استدلالی بر این واقعیت استوار است که، هرگاه یک ترکیب فصلی درست باشد، آنگاه حداقل یکی از دو مؤلفه آن نیز باید درست باشد. استدلالهایی با این صورت فراوان بکار میروند.
قیاس فصلی را بصورت زیر نمادین میکنیم:
p۲: ~p
∴ q
و برای اعتبار آن جدول ارزش زیر را تشکیل میدهیم:
| p | q | p ⋁ q | ~p |
| T | T | T | F |
| T | F | T | F |
| F | T | T | T |
| F | F | F | T |
در این جدول، ستونهای آغازین یا راهنما همهی مقادیر ارزش مختلف قابل جانشین برای متغیرهای گزارهای p و q را نشان میدهند. ستون سوم جدول را با مراجعه به ستونهای اول و دوم، و ستون چهارم را فقط با مراجعه به ستون اول با مقادیر ارزش پر کردهایم. در این جدول، سطر سوم تنها سطری است که در آن مقدار ارزش T برای مقدمات (ستونهای سوم و چهارم) آمده است. بعلاوه نتیجه هم (ستون دوم) در این سطر دارای مقدار T است. بنابراین مطابق با آنچه جدول ارزش نشان میدهد، این صورت استدلال هیچ مورد جانشینی ندارد که در آن مقدمات درست و نتیجه نادرست باشد، و این ثابت میکند که صورت استدلال مورد آزمون معتبر است. آنگونه که در این فصل بکار میبریم، اصطلاح قیاس فصلی، نام یک صورت استدلالی مقدماتی، که هم اکنون ثابت شد معتبر است، خواهد بود. این صورت همیشه معتبر است و از اینجاست که در منطق جدید قیاس فصلی همیشه به یک صورت استدلالی مقدماتی معتبر ارجاع دارد. اما در منطق سنتی، قیاس فصلی بهصورت گستردهتر و به هر قیاسی که دارای یک گزاره فصلی است، گفته میشود. بعضی از این قیاسها میتواند معتبر نباشد. بنابراین باید مشخص باشد که مراد از "قیاس فصلی" کدامیک از آنهاست. اینجا منظور ما برداشت باریکتر آن است.
در اینجا نیز ضرورت است تا جدول ارزش بدقت خوانده شود، یعنی ستونی که نتیجه را نشان میدهد (ستون دوم از سمت چپ) و ستونهایی که مقدمات را نشان میدهند (ستونهای سوم و چهارم از سمت چپ) دقیقاً مشخص شوند. فقط با بکار گرفتن این سه ستون است که میتوان اعتبار این صورت استدلال موردبررسی را با اطمینان تعیین کرد. توجه کنید که دقیقاً همین جدول میتواند برای آزمون اعتبار صورت استدلالی کاملاً متفاوت بکار رود، یعنی صورت استدلالی که مقدمات آن ستونهای دوم و سوم باشند و نتیجه آن توسط ستون چهارم نشان داده شود. با توجه به اولین سطر میتوان دید که این استدلال نامعتبر است. جداول ارزش، برای آزمون اعتبار هر نوع کلی استدلال، که آنها را در اینجا بررسی میکنیم، یک روش تمام ماشینی را مهیا میکنند.
اینجا، جایی است که میتوانیم پیشگذارده خود، یعنی برگردان هر رویداد عبارت "اگر- آنگاه" به نماد استلزام مادی ⊂ را موجه نماییم. در قسمت قبل گفته بودیم در همه گونههای کلی استدلالهای معتبر، که در اینجا با آنها سر و کار داریم و شامل گزارههای "اگر- آنگاه" هستند، اگر این گزارهها را به استلزام مادی تعبیر نماییم، بازهم معتبر خواهند ماند. از جدول ارزش میتوان برای محق بودن این ادعا استفاده کرد و برگردان "اگر – آنگاه" را به نماد نعل اسبی موجه نمود.
■ قیاس استثنایی
در زیر سادهترین استدلال که بداهتاً معتبر مینماید و شامل یک گزاره شرطی است، آمده:
p۱: p ⊃ q
p۲: p
∴ q
اعتبار این صورت استدلال، که به قیاس استثنائی (هچنین: قاعده وضع، قاعده تصدیق) مشهور است، را میتوان با جدول ارزش زیر نشان داد:
| p | q | p ⊃ q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
در اینجا دو مقدمهی استدلال با ستونهای اول و سوم و نتیجه استدلال با ستون دوم نشان داده شده. فقط سطر اول نشاندهنده موارد جانشین است که در آنها هر دو مقدمه درست هستند و T نیز در ستون دوم نشان میدهد که در اینگونه استدلالها نتیجه درست است. این جدول ارزش، اعتبار هر استدلال با صورت قیاس استثنائی را تثبیت میکند.
■ قیاس اقترانی
اگر یک گزاره شرطی درست باشد، آنگاه اگر تالی آن نادرست باشد، مقدم هم نیز باید نادرست باشد. این صورت استدلالی برای وقتیکه میخواهند نادرستی یک گزاره موردحمله را نشان دهند، بسیار رایج است. یک آموزگار برجسته مذهبی که پای میفشرد سفر پیدایش هرگز بهمعنی رساله علمی بودن نیست، این استدلال کوتاه را میآورد.
Rabbi Ammiel Hirsch, “Grand Canyon,” The New York Times, 10 October 2005.
این استدلال را میتوان بهصورت زیر نمادین کرد.:
p۱: p ⊃ q
p۲: ~q
∴ ~p
اعتبار این صورت منطقی که مشهور به قیاس اقترانی (هچنین: قاعده رفع یا قاعده انکار) است، را با جدول ارزش زیر نشان میدهیم.
| p | q | p ⊃ q | ~q | ~p |
| T | T | T | F | F |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | T | T |
در اینجا نیز هیچ مورد جانشینی وجود ندارد که در آن مقدمات، p ⊃ q و q~ هردو درست و نتیجه، p~، نادرست باشد.
■ قیاس شرطی
ازجمله قیاسهای آشکارا معتبر دیگر، قیاسی است که فقط از گزارههای شرطی تشکیل شده است. در زیر یک مثال از این نوع قیاس آمده:
اگر اولین فرد محلی دروغ بگوید، آنگاه اولین فرد محلی انکار خواهد کرد که سیاستمدار است.
بنابراین اگر اولین فرد محلی یک سیاستمدار باشد، آنگاه اولین فرد محلی انکار خواهد کرد که سیاستمدار است.
صورت نوعی این استدلال در زیر آمده:
p۱: p ⊃ q
p۲: q ⊃ r
∴ p ⊃ r
ازآنجاکه این استدلال، که به آن قیاس شرطی (یا قیاس شرطی محض) میگویند، دارای سه متغیر گزارهای متمایز است، جدول ارزش آن باید دارای سه ستون آغازین (راهنما) و بعلاوه دارای هشت سطر برای نشان دادن همه موردهای جانشین ممکن باشد. بهعلاوهی سه ستون آغازین، سه ستون اضافی دیگر نیز که دوتای آن برای دو مقدمه و یکی دیگر برای نتیجه است، موردنیازاند. این جدول در زیر آمده.
| p | q | r | p ⊃ q | q ⊃ r | p ⊃ r |
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | T |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | T |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
در تشکیل جدول برای پر کردن ستون چهارم به ستونهای اول و دوم، و برای پر کردن ستون پنجم به ستونهای دوم و سوم، و برای پر کردن ستون سوم به ستونهای اول و سوم رجوع کردهایم. در مراجعه به جدول کاملشده مشاهده میکنیم که مقدمات فقط در سطرهای اول، پنجم، هقتم و هشتم همگی درست هستند که در این سطرها نتیجه نیز درست است. این جدول ارزش، اعتبار صورت استدلال را پابرجا و ثابت میکند که قیاس شرطی اعتبار خود را در برگردان گزارههای شرطی با استفاده از نماد نعل اسبی همچنان حفظ میکند.
بهاندازه کافی مثال برای روش صحیح آزمون استدلال با استفاده از تکنیک جدول ارزش آوردهایم. و احتمالاً بهاندازه کافی نیز سعی شد تا نشان دهیم اعتبار هر استدلال شامل گزارههای شرطی، وقتی شرطیها به استلزام مادی برگردانده شوند، همچنان باقی خواهند ماند. اگر شکی هم باقی است، میتواند توسط خواننده با آوردن و برگرداندن و آزمون مثالهایی مانند اینها برطرف گردد.
برای آزمون استدلالهای پیچیدهتر جداول ارزش پیچیدهتر نیاز است، زیرا برای هر متغیر اضافی، یک ستون آغازین (یا همان راهنما) اضافی نیاز است. برای یک صورت فقط با دو متغیر، دو ستون آغازین (راهنما) و همچنین چهار سطر نیاز خواهد بود. اما برای یک صورت با سه متغیر، مانند قیاس شرطی، سه ستون نیاز است، و جدول دارای هشت سطر خواهد شد. برای آزمون صورت استدلال زیر (که به دو وجهی ساختی موسوم است):
p۱: (p ⊃ q) • (r ⊃ s)
p۲: p ⋁ r
∴ q ⋁ s
با چهار متغیر گزارهای متمایز به چهار ستون آغازین و ۱۶ سطر نیاز است. بهطورکلی برای آزمون یک صورت استدلال که دارای n متغیر متمایز است به یک جدول ارزش با n ستون آغازی و ۲n سطر نیازمند هستیم.
■ صورتهای رایج نامعتبر:
اینجا باید به دو صورت استدلال نامعتبر توجه خاص نماییم، زیرا آنها دارای شباهتی ظاهری به دو صورت معتبر دارند و بنابراین اغلب موجب فریب خواننده و نویسندگان بیدقت میگردند.
۱- مغالطه وضع تالی بهصورت زیر نمادین میشود:
p۱: p ⊃ q
p۲: q
∴ p
گرچه ریخت آن شبیه قیاس استثنایی است، ولی در صورت بسیار متفاوت هستند و این صورت اخیر مطمئناً معتبر نیست. بنابراین، وقتی کسی اصرار میکند که چون طرفداران حزب سبز مدافع محیطزیست هستند، هر مدافع محیط زیست باید طرفدار حزب سبز باشد، آنگاه وی مرتکب مغالطه وضع تالی گردیده.
۲- مغالطه رفع مقدم که ریخت آن چیزی شبیه قیاس اقترانی است و بهصورت زیر نمادین میشود.
p ⊃ q
~p
∴ ~q
بهسادگی و با استفاده از جدول ارزش میتوان نشان داد که هردوی این مغالطههای رایج، بیاعتبار هستند. در جدول ارزش هریک از آنها سطری وجود دارد که در آنها مقدمات این دو استدلال مغالطه آمیز درست ولی نتیجه نادرست است.
■ موردهای جانشین و صورتهای نوعی
یک استدلال دادهشده میتواند مورد جانشین چندین صورت استدلالی باشد. بنابراین قیاس منفصله معتبر را که میتوان بهصورت زیر نمادین کرد:
R ⋁ W
~R
∴ W
میتواند یک مورد جانشین صورت استدلال زیر باشد:
p ⋁ q
~q
∴ q
و همچنین میتواند یک مورد جانشین صورت استدلال نامعتبر زیر باشد:
p
q
∴ r
آشکار است که در صورت آخری نمیتوان r را از p و q به گونه معتبر نتیجه گرفت. پس روشن است که: از یک صورت استدلالی نامعتبر میتوان موارد جانشین معتبر یا نامعتبر را به دست آورد، بنابراین، برای تعیین اعتبار یک استدلال، باید در جستجوی صورت نوعی آن استدلال بود. فقط صورت نوعی یک استدلال میتواند بهطور دقیق ساختار آن استدلال را آشکار نماید؛ به خاطر همین نیز هست که میگوییم وقتی صورت نوعی یک استدلال معتبر باشد، آنگاه آن استدلال معتبر است.
در همین مثال قبلی دیدیم که یک استدلال (R⋁W و R~، بنابراین W) میتواند مورد جانشین دو صورت استدلال باشند. اولین صورت استدلال (p⋁q و p~، بنابراین q) معتبر است، و چون این صورت، صورت نوعی استدلال دادهشده است، از اعتبار آن میتوان اعتبار استدلال دادهشده را نتیجه گرفت. دومین صورت استدلالی نامعتبر است، اما یک صورت استدلالی که صورت نوعی نیست، نمیتواند نشان دهد که یک استدلال دادهشده نامعتبر است.
باید بر این نکته تأکید کنیم که: یک صورت استدلال معتبر فقط میتواند استدلالهای معتبر را بهعنوان مورد جانشین داشته باشد. به عبارت دیگر، همه موارد جانشین یک صورت معتبر باید معتبر باشند. این همان چیزی بود که بهوسیله اثبات بروش جدول-ارزش برای اعتبار یک صورت استدلالی معتبر ثابت شد، که نشان میدهد موارد جانشین ممکن برای یک صورت معتبر، به قسمی که مقدمات آن درست و نتیجه نادرست باشد، وجود ندارد.
تمرین
الف- با استفاده از جدول ارزش-- اعتبار یا بیاعتباری هریک از صورتهای استدلالی تمرین ۱ گروه ب در ف۹.ق.۴ را برآورد نمایید.
ب- با استفاده از جدول ارزش-- اعتبار یا بیاعتباری هریک از استدلالهای زیر را برآورد نمایید.
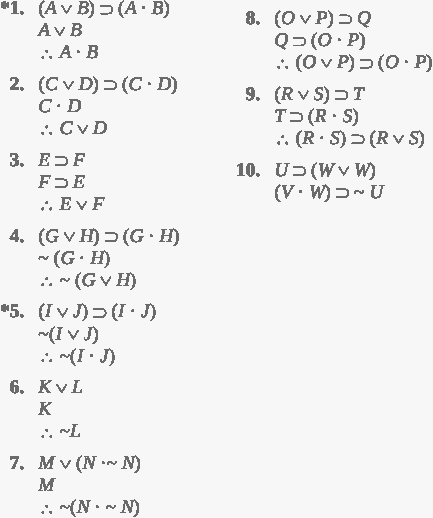
حل ستاره دار ها

ج- با استفاده از جدول ارزش-- اعتبار یا بیاعتباری هریک از استدلالهای زیر را برآورد نمایید.
۱- اگر آنگولا موفق به ثبات شود، آنگاه بوتسوانا و هم چاد روشهای لیبرالی بیشتری در پیش خواهند گرفت. اما بوتسوانا روشهای لیبرالی بیشتری در پیش نخواهد گرفت. بنابراین آنگولا موفق به ثبات نمیشود.
۲- اگر دانمارک از پیوستن به اتحادیه اروپا خودداری کند، آنگاه، اگر استونیا در حوزه نفوذ روسیه باقی بماند، آنگاه فنلاند از سیاست توسعه بازار آزار خودداری خواهد کرد. استونیا در حوزه روسیه باقی خواهد ماند. بنابراین اگر دانمارک از پیوستن به اتحادیه اروپا خودداری کند، آنگاه فنلاند از سیاست توسعه بازار آزاد خودداری خواهد کرد.
۳- اگر یونان نهادهای دموکراتیک خود را توسعه دهد، آنگاه مجارستان سیاستهای غیر واسطه را بیشتر تعقیب خواهد کرد. اگر یونان نهادهای دموکراتیک خود را توسعه دهد، آنگاه دولت ایتالیا احساس تهدید کمتری میکند. بنابراین، اگر مجارستان سیاستهای غیر واسطه را بیشتر تعقیب کند، آنگاه دولت ایتالیا احساس تهدید کمتری خواهد کرد.
۴- اگر ژاپن به افزایش صادرات اتومبیل ادامه دهد، آنگاه کره یا لائوس از افت اقتصادی رنج خواهند برد. کره از افت اقتصادی رنج نخواهد برد. بنابراین اگر ژاپن به افزایش صادرات اتومبیل ادامه دهد، آنگاه لائوس از افت اقتصادی رنج خواهد برد.
۵- اگر مونتانا خشکی شدیدی را متحمل شود، آنگاه اگر نوادا بارش معمول و سبک خود را داشته باشد، ذخیره آب اورگان بسیار کاهش مییابد. نوادا بارش معمولی سبک خود را داشت. بنابراین اگر ذخیره آب اورگان بسیار کاهش یابد، آنگاه مونتانا خشکی شدیدی را تحمل میکند.
۶- اگر برابری فرصتها محقَق شود، آنگاه باید به مردمان توسعهنیافته پیشین، هماکنون فرصتهای ویژه داده شود. اگر باید به مردمان توسعهنیافته پیشین، هماکنون فرصتهای ویژه داده شود، آنگاه بعضی از مردم درمآنهای ترجیحی دریافت خواهند کرد. اگر بعضی از مردم درمآنهای ترجیحی دریافت کنند، آنگاه برابری فرصتها محقق نمیشود. بنابراین برابری فرصتها محقق نمیشود.
۷- اگر خواست تروریستها برآورده شود، آنگاه بیقانونی پاداش خواهد گرفت. اگر خواست تروریستها برآورده نشود، آنگاه گروگآنهای بیگناه گشته خواهند شد. بنابراین یا بیقانونی پاداش خواهد گرفت یا گروگآنهای بیگناه گشته خواهند شد.
۸- اگر مردم کاملاً منطقی باشند، آنگاه یا همهی رفتار و کردار شخص را میتوان از قبل پیشبینی کرد یا جهان اساساً قطعی است. نه همهی رفتار و کردار شخص را میتوان از قبل پیشبینی کرد. بنابراین، اگر جهان اساساً قطعی نباشد، آنگاه مردم کاملاً منطقی نیستند.
۹- اگر کشورهای مصرفکننده نفت به رشد ادامه دهند، آنگاه صادرات نفت افزایش خواهد یافت یا ذخایر محلی نفت تمام خواهد شد. اگر صادرات نفت افزایش یابد و ذخایر محلی نفت تمام شود، ملتها سرانجام تهیدست خواهند شد. بنابراین اگر کشورهای مصرفکننده نفت به رشد ادامه دهند، سرانجام ملتها تهیدست خواهند شد.
۱۰- اگر کشورهای مصرفکننده نفت به رشد ادامه دهند، آنگاه صادرات نفت افزایش خواهد یافت و ذخایر محلی نفت تمام خواهد شد. اگر صادرات نفت افزایش یابد یا ذخایر محلی نفت تمام شود، ملتها سرانجام تهیدست خواهند شد. بنابراین اگر کشورهای مصرفکننده نفت به رشد ادامه دهند، سرانجام ملتها تهیدست خواهند شد.
حل ستاره دار ها

