صورت های گزارهای و همارزی مادی
منطق گزارهای و گزارههای تابع-ارزش
درآمد به منطق فصل ۹ قسمت ۸
در قسمت قبل سخن از صورت استدلال رفت و چهار صورت استدلالی معتبر بسیار پرکاربرد را به قرار قیاس فصلی، قیاس استثنائی، قیاس اقترانی و قیاس شرطی بعنوان صورتهای معتبر مقدماتی معرفی کردیم. دراین قسمت ابتدا مفهوم صورت گزارهای را به میان میآوریم و از صورتهای توتولوژیک، ممکن و متناقض سخن گفته و سرانجام خاطرنشان میکنیم برای هر صورت استدلال معتبر صورتی گزارهای توتولوژیک (منطقاً درست) نیز برای هر صورت استدلال نامعتبر صورتی ممکن یا متناقض هست.
۸.۹ صورت های گزارهای و همارزی مادی
صورت گزارهای
Statement Form
آرایهای از نمادها که نشاندهنده ساختار منطقی گزاره است، این آرایه شامل متغیرهای گزارهای و نه خود گزاره است.
صورت گزارهای فصلی
Disjunctive Statement Form
صورت گزارهای نمادین شده با p⋁q؛ که موردهای جانشین آن گزارههای فصلی هستند.
صورت نوعی
صورت خاص
Specific Form
هنگام ارجاع به گزارهای دادهشده، آن صورت گزارهای که از آن، وقتی گزاره ساده متفاوتی بهطور یکنواخت برای هر متغیرهای گزارهای در آن صورت جانشین شده گزاره دادهشده حاصل گردیده.
صورت استدلال
Argument form
دنبالهای از صورتهای گزارهای که همه بجز آخرین صورت مقدمه و آخرین صورت نتیجه است.
توتولوژی
منطقاً درست
درستی منطقی
Tautology
Logical truth
صورت گزارهای که همه موارد جانشین آن درست باشند.
تناقض
Contradiction
صورت گزارهای که همه موارد جانشین آن نادرست هستند.
یا
عبارت گزارهای که
به ضرورت نادرست است.
همارزی مادی
Material equivalence
یک رابط تابع ارزش (نمادین شده با ≡) که دو گزاره را به هم پیوند میدهد. دو گزاره وقتی همارز مادی هستند که هر دو درست یا هر دو نادرست باشند— یعنی، وقتی آنها دارای مقدار ارزش یکسان باشند. گزارههای همارز مادی همیشه مستلزم مادی یکدیگرند.
آ. صورتهای گزارهای و گزارهها:
در این قسمت به انگاره صورت گزارهای که در قسمت قبل آن را تلویحی مفروض گرفته بودیم، صراحت میدهیم. از یکسو میان نسبت استدلال به صورت استدلال و از سوی دیگر نسبت گزاره به صورت گزاره یک توازی دقیق وجود دارد. تعریف صورت گزارهای چنین چیزی را آشکار میکند:
صورت گزارهای دنباله دلخواهی از نمادها به شمول متغیرهای گزارهای و نه خود گزاره است، آنگونه که وقتی گزارههایی را بهطور یکنواخت، یعنی یک گزاره یکسان برای یک متغیر در سرتاسر صورت گزارهای، جانشین متغیرهای گزارهای نماییم، آنگاه نتیجه حاصل از این جانشینی یک گزاره باشد.
ازاینقرار p∨q یک صورت گزارهای است، زیرا وقتی گزاره جانشین متغیرهای p و q نماییم، حاصل یک گزاره خواهد بود. چون گزارهی حاصل یک ترکیب فصلی است، به p∨q یک صورت گزارهای فصلی گفته میشود. به همین قیاس p•q و p⊃q را صورتهای گزارهای عطفی و شرطی مینامند. همینطور p~ صورت نقضی نامیده. همانطور که به هر استدلال از یک صورت استدلال نوعی یک مورد جانشین آن صورت گفته، به هر گزاره از یک صورت خاص نیز یک مورد جانشین آن صورت گزارهای خواهیم گفت. نیز همانطور که صورت نوعی یک استدلال دادهشده را تشخیص دادیم، صورت نوعی یک گزاره دادهشده نیز عبارت است از آن صورت گزارهای که گزاره دادهشده از آن بهوسیله جانشینی سازگار یک گزاره ساده برای متغیرهای گزارهای مختلف به دست آمده باشد. بنابراین p∨q صورت نوعی گزاره «زندانی نابینا یک کلاه قرمز دارد یا زندانی نابینا یک کلاه سفید دارد» است.
با تعریفی که از «صورت گزارهای» در دست داریم، اکنون میتوان تعریف دقیقتر و کوتاهتر از «صودت استدلال» ارائه کرد:
صورت استدلال، دنبالهای از صورتهای گزارهای است، که در آن همه به جز آخرین صورت گزارهای، مقدمات هستند، و آخرین شکل صورت گزارهای نتیجه است.
ب. صورتهای گزارهای توتولوژیک، متناقض و ممکن:
گزاره «لینکلن ترور شده است» (نمادین شده به شکل L) و گزاره «لینکلن ترور شده است یا نشده است» (نمادین شده به شکل L⋁~L) هردو آشکارا درست هستند. ولی، میگوییم درستی آنها هرکدام "به طریق مختلف" است، یا درستی آنها از "نوع مختلف" است. به همین طریق «واشنگتن ترور شده است» (نمادین شده شکل W) و گزاره «واشنگتن ترور شده است و ترور نشده است» (نمادین شده به شکل W•~W) هردو آشکارا نادرست هستند، اما هریک "به طریق مختلف" نادرست هستند و یا نادرستی آنها از "نوع مختلف" است. این تفاوت در «نوع» درستی یا نادرستی بسیار با اهمیت و نیز بسیار گسترده است.
اینکه گزاره L درست است و گزاره W نادرست است، برخاسته از واقعیات تاریخی هستند، واقعیاتی درباره آنگونه که رویدادها رویدادهاند. یک ضرورت منطقی درباره آنها وجود ندارد. رویدادها ممکن بود جور دیگر روی دهند. بنابراین مقدار ارزش گزارههای L و W را باید با مطالعه مشاهدات تاریخی کشف کرد. اما گزاره L∨~L گرچه درست است ولی یک درستی تاریخی نیست. در اینجا ضرورت منطقی حضور دارد: رویدادها نمیتوانستند آن را نادرست سازند، و درستی آن فارغ از هر بررسی تاریخی خاص است. درستی گزاره L∨~L یک درستی منطقی، یک درستی صوری است و صرفاً به موجب صورت خود است که درست است. این گزاره مورد جانشین یک صورت گزارهای است که همه موردهای جانشین آن، گزارههای درست هستند.
یک صورت گزارهای که فقط موردهای جانشینی درست دارد، یک صورت گزارهای توتولوژیک، یا یک توتولوژی ( ریشه یونانی: tauto: همان+ logos: گفتن / بازگویی سخن گفتهشده) [نیز منطقاً درست] نامیده میشود. برای آنکه نشان دهیم صورت گزارهای p∨~p یک توتولوژی است، جدول ارزش آن را تشکیل میدهیم.
| p | ~p | p ∨ ~p |
| T | F | T |
| F | T | T |
ازآنجاکه صورت موردبررسی فقط یک متغیر گزارهای دارد، جدول ارزش آن نیز یک ستون آغازین یا راهنما خواهد داشت. بنابراین فقط دو سطر است که همه موارد ممکن جانشینی را نشان میدهند. در ستون گزاره موردبررسی فقط T وجود دارد، و این واقعیت نشان میدهد که همه موردهای جانشین آن درست هستند. هر گزاره که مورد جانشین یک صورت گزارهای توتولوژیک باشد، بهموجب صورت خود درست خواهد بود و به آن گزاره توتولوژیک یا یک توتولوژی گفته.
یک توتولوژی تابع-ارزش مانند p⋁~p آشکارا و به معنای دقیق آن به ضرورت درست است، یعنی نمیتواند برای هر ترکیب از مقادیر ارزشِ متغیر(های) گزارهای خود نادرست باشد. همانطور که یک صورت استدلال معتبر و تابع-ارزش نمیتواند دارای همه مقدمات درست و نتیجه نادرست برای هر ترکیب از مقادیر ارزش برای متغیرهای گزارهی تشکیل دهنده خود باشد، یک صورت گزارهای توتولوژیک نمیتواند برای هر ترکیب از مقادیر ارزش برای متغیر(های) گزارهای سازنده خود نادرست باشد. این واقعیت را ممکن است بتوان با آشکاری با صورت استدلالی موسوم به مصادره به مطلوب [petitio principii] (وامگیری از پرسش) نشان داد.
p۱: p
∴ p
و نیز صورت شرطی متناظر آن:
p ⊃ p
این صورت استدلال آشکارا یک وامگیری از پرسش با فرض آنچه در نتیجه خود دارد از مقدمات خود است. با این حال، این یک صورت استدلال معتبر است، زیراکه با ساختن جدول ارزش آن مشخص میشود.
| p | ∴ |
| T | T |
| F | F |
این صورت استدلال نمیتواند همه مقدمات درست و نتیجهگیری نادرست داشته باشد، زیرا وقتی مقدمات آن، یعنی p، درست است، نتیجه آن، یعنی p، درست است، و وقتی که نتیجه آن، یعنی p، نادرست است، مقدمات آن، یعنی p، نادرست است. در فصل ۵ (مغالطه)، اشاره کردیم که این گونه مغالطه یک استدلال دوری (circular) معتبر موسوم به مصادره به مطلوب (petitio principii)، لیکن ناچیز و غیر موثر است. اکنون میتوان دقیقتر گفت که گرچه صورت این استدلال معتبر است و مورد جانشینی آن میتواند صحیح باشد، اما غیر-بازنمایانگر (non-demonstrative) است. بدین معنی که هیچ استدلالی از این صورت خاص نمیتواند درستی نتیجه خود را بازنمایاند، چراکه درستی هر گزاره در مقدمه(های) خود را مفروض گرفته است. هیچ فرد عاقلی که در مورد درستی گزاره «موجودات هوشمند در جای دیگری در جهان هستی وجود دارند» تردید یا تعجب میکند، نباید و قانع نمیشود از اینکه کسی درستی این گزاره را از خود دریافته باشد!
بطور مشابه، گزاره شرطی با صورت
p ⊃ p
یک توتولوژی است و این را میتوان به سادگی با ساختن جدوب ارزش آن دید.
| p | p ⊃ p |
| T | T |
| F | T |
گزاره شرطی p ⊃ p توتولوژی است چرا که نمیتواند نادرست باشد. زیرا اگر مقدم آن، یعنی p، درست باشد، تالی آن، یعنی p، هم درست است و اگر تالی آن، یعنی p، درست باشد، مقدم آن، یعنی p، هم درست است. این مورد حدی اعتبار و توتولوژی بودن بعداً در قسمت ۸.۹➥ توضیح داده خواهد شد و ارتباط مهم بین یک صورت استدلال معتبر و صورت گزاره شرطی توتولوژیک متناظر آن را در بخش ۸.۹، یعنی وقتی قاعده رهان شرطی را موجه خواهیم کرد، بکار خواهیم زد.
به یک صورت گزارهای که فقط موردهای جانشینی نادرست دارد تناقض یا یک (صورت) متناقض گفته میشود، که منطقاً نادرست است. صورت گزارهای p•~p یک تناقض است، زیرا در جدول ارزش، در ستون زیر آن فقط F وجود دارد، که نشان میدهد همه موردهای جانشین آن نادرست هستند. هر گزارهای مانند W•~W که خود مورد جانشینی یک صورت گزارهای متناقض باشد، بهموجب صورت خود نادرست است؛ به چنین گزارهای یک تناقض گفته میشود.
به صورتهای گزارهای که دارای موارد جانشینی درست و هم نادرست باشند، صورت گزارهای ممکن گفته میشود. به هر گزاره که صورت نوعی آن ممکن است، یک گزاره ممکن گفته. (باید یادآوری شود ما اینجا یک گزاره ساده را نه منطقاً درست و نه منطقاً نادرست در نظر گرفتهایم. فقط گزارههای ساده ممکن در اینجا مجوز حضور دارند.) بنابراین صورتهای:
p, ~p, p • q, p ∨ q,p ⊃ q
صورتهای گزارهای ممکن هستند و همچنین گزارههای:
L, ~L, L • W, L ∨ W, L ⊃ W
گزارههای ممکن هستند، زیرا جدول ارزش آنها وابسته و مشروط به محتوی آنها است و نه به صورت آنها.
همه صورتهای گزارهاییِ توتولوژیک یا متناقض یا ممکن به آشکاری مثالهایی که در بالا آمد نیستند. برای مثال، گرچه جدول ارزش نشان میدهد صورت گزارهای:
[(p⊃q)⊃p]⊃p
یک توتولوژی است اما صورت ظاهر آن هرگز چنین چیزی را نشان نمیدهد.
| p | q | p ⊃ q | (p ⊃ q) ⊃ p | [(p ⊃ q) ⊃ p] ⊃ p |
| T | T | T | T | T |
| T | F | F | T | T |
| F | T | T | F | T |
| F | F | T | F | T |
در جدول ارزش میتوان دید صورت گزارهای [(p⊃q)⊃p]⊃p (موسوم به قانون پیرس) یک توتولوژی است زیرا برای هر مقدار ارزش برای متغیرهای گزارهای سازنده آن دارای مقدار ارزش درست است. ستون صورت گزارهای p⊃q و ستون صورت گزارهای (p⊃q)⊃p نشان میدهند هردو این صورتهای گزارهای ممکن هستند زیرا هر دو در حداقل برای یک ترکیب از مقادیر ارزش برای متغیرهای گزارهای p و q درست هستند و نیز هر دو در حداقل برای یک ترکیب از مقادیر ارزش برای متغیرهای گزارهای p و q نادرست هستند.
ج. همارز مادی:
همارزی مادی مانند فاصل (∨)، عاطف (•) و استلزام مادی (⊂) که رابطهای تابع-ارزش هستند، نیز یک رابط تابع ارزش است. همانطور که قبلاً توضیح دادیم، مقدار ارزش هر رابط تابع-ارزش وابسته به (تابعی از) درستی و نادرستی گزارههایی است که آنها را به هم ربط میدهد. به این جهت است که میگوییم ترکیب فصلی A و B وقتی درست است که A درست باشد یا B درست باشد یا وقتیکه هردوی آنها درست باشند. همارزی مادی نیز یک رابط تابع-ارزش است که میگوید، گزارههایی را که به هم میپیونداند دارای مقدار ارزش یکسان هستند. بنابراین دو گزاره که در مقدار ارزش معادل (همارز) باشند همارز مادی هستند. یک تعریف سرراست از همارز مادی بدین قرار است: دو گزاره را همارز مادی گویند هرگاه هر دو درست یا هردو نادرست باشند. همانگونه که نماد فصل گُوِه (∨)، و نماد استلزام مادی نعل اسبی (⊂) است، برای همارزی مادی نیز یک نماد، یعنی سه خطی " ≡"، وجود دارد. همان روش را که در مورد جدول ارزش گوه و نعل اسبی بکار بردیم، میتوان برای جدول ارزش سه خطی بکار برد. در زیر جدول ارزش همارزی مادی، ≡ ، آمده است.
| p | q | p ≡ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
هر دو گزاره درست مستلزم مادی یکدیگر هستند و این پیامدِ معنی استلزام مادی است. بنابراین، وقتی دو گزاره همارز مادی هستند، باید مستلزم یکدیگر باشند، چراکه هردو درست یا هردو نادرست هستند.
ازآنجاکه هر دو گزاره همارز مادی A و B مستلزم یکدیگرند، میتوان از همارز مادی بودن آنها نتیجه گرفت که B درست است اگر A درست باشد و نیز B درست است فقط اگر A درست باشد. چون همارزی مادی مستلزم هردوی این رابطههاست، بنابراین نشان سه خطی، ≡، را چنین میخوانیم که میگوید "اگر و فقط اگر".
در گفتار رایج گاهی از این رابط منطقی استفاده میشود. برای مثال یک فرد ممکن است بگوید، من به تماشای مسابقه فینال خواهم رفت، اگر و فقط اگر بتوانم بلیت تهیه کنم. من به تماشای مسابقه فینال خواهم رفت، اگر بتوانم بلیت تهیه کنم، اما اگر فقط بتوانم بلیت تهیه کنم به تماشای مسابقه فینال خواهم رفت. بنابراین رفتن من به تماشای مسابقه فینال و به دست آوردن بلیت توسط من همارز مادی هستند.
همانطور که قبلاً گفتهایم هر استلزام یک گزاره شرطی است. دو گزاره A و B که همارز مادی هستند، مستلزم درستی گزاره شرطی A⊃B و همچنین مستلزم درستی گزاره شرطی B⊃A هستند. از آنجا که وقتی همارزی مادی برقرار است، استلزام دوسویه است، در بیشتر موارد به گزاره A≡B یک دو شرطی گفته.
گزاره دوشرطی "A اگر و فقط اگر B"، نمادین شده با A ≡ B، به این دلیل دو شرطی نامیده میشود که از نظر منطقی همارز است (همانطور که در قسمت ۸.۹ نشان داده خواهد شد) با عطف دو گزاره شرطی، یعنی (A⊃B)•(B⊃A).
اکنون میتوانیم روابط مهم بین یک دو شرطی (یک همارزی مادی)، یک شرطی، و شرط لازم و کافی (همانطور که در بخش ۳.۹ بحث شد) را بیان کنیم.
«q اگر p» یا «اگر p، آنگاه q» (p شرط کافی برای q است): p⊃q.
«q فقط اگر p» یا (p شرط لازم برای q است): q⊃p.
«q اگر و فقط اگر p» (یا p شرط کافی برای q و p شرط لازم برای q است): (p⊃q)•(q⊃p).
«p اگر و فقط اگر q» (یا q شرط کافی برای p و q شرط لازم برای p است): (q⊃p)•(p⊃q).
«p اگر و فقط اگر q» (یا q شرط کافی برای p و q شرط لازم برای p است): p≡q.
| p | q | p ⊃ q | q ⊃ p | (q ⊃ p) • (p ⊃ q) | (p ⊃ q)•(q ⊃ p) | p ≡ q |
| T | T | T | T | T | T | T |
| T | F | F | T | F | F | F |
| F | T | T | F | F | F | F |
| F | F | T | T | T | T | T |
همانطور که بعدتر در قسمت ۹.۹ خواهیم دید صورتهای گزارهای (در جدول ارزش بالا) در سه ستون آخر بطور منطقی با یکدیگر همارز هستند. بنابراین، گزاره دو شرطی A≡B دو شرط "A اگر و فقط اگر B" را در بر میگیرد - یعنی B⊃A و A⊃B — همانطور که با عطف آن دو عبارت شرطی در عبارت منطقاً همارز (A⊃B)•(B⊃A) نشان داده میشود.
پنج عملگر منطقی تابع-ارزشی (یعنی چهار رابط و یک عملگر منطقی غیر پیوندی) وجود دارد که استدلالهای استنتاجی عموماً به آنها بستگی دارند: عطف، فصل، استلزام مادی و همارزی مادی. اکنون بحث ما درباره این مجموعه چهارگانه دیگر تمام است.
| مرور کلی | ||||
| چهار رابط تابع-ارزش | ||||
| رابط تابع-ارزش | نماد | نوع گزاره | نام مؤلفهها | مثال |
| و | • | عطفی | فصل | پرویز کارمند است و پروین دانشجو است. |
| یا | ∨ | فصلی | عطف | پرویز کارمند است یا پروین خواننده است. |
| اگر . . . آنگاه | ⊃ | شرطی | مقدم-تالی | اگر پرویز بخواند آنگاه پروین بدخلق میشود. |
| اگر و تنها اگر | ≡ | دو شرطی | مؤلفه | پروین بدخلق میشود اگر و تنها اگر پرویز بخواند. |
برای اینکه خواننده بتواند جدول ارزش تعریفی را برای هر عملگر منطقی به خاطر بسپارد، پنج قاعده کلی زیر را در پیش میگذاریم
عطفی: یک عطفی وقتی درست است که هر دو عطف آن درست باشد. در غیر این صورت نادرست است.
فصلی: یک فصلی وقتی نادرست است که هر دو فصل آن نادرست باشد. در غیر این صورت درست است
شرطی: یک شرطی فقط وقتی نادرست است که مقدم آن درست و تالی آن نادرست باشد. در غیر این صورت درست است
دوشرطی: یک دوشرطی تنها وقتی درست است که عبارتهای گزارهای دو طرف نماد ۳ خطی دارای مقدار ارزش یکسانی باشند. در غیر این صورت نادرست است.
نقیض: یک نفض وقتی درست است که گزاره مورد نقض نادرست باشد. در غیر این صورت نقضی نادرست است. (یک نقیض دارای مقدار ارزش مخالف گزاره نقض شده است.)
د. استدلال، گزارههای شرطی و توتولوژی:
به هر استدلال یک گزاره شرطی نظیر میشود که مقدم آن عطف مقدمههای استدلال است و تالی آن نتیجه آن استدلال است. بنابراین یک استدلال که به صورت قیاس استثنائی است:
p۱: p ⊃ q
p۲: p
∴ q
دارای یک گزاره شرطی با صورت:
[(p ⊃ q) • p] ⊃ q
است.
یک صورت استدلال وقتی معتبر است که نتواند دارای همه مقدمات درست و نتیجه نادرست باشد. یک گزاره شرطی نادرست است اگر و تنها اگر مقدم آن درست و نتیجه آن نادرست باشد. شرطی بالا فقط در حالتهایی نادرست است که هر دو مقدمه - p⊃q و p - درست و نتیجه، یعنی q، نادرست باشد. اگر یک صورت استدلال معتبر باشد، چنین حالتهایی وجود نخواهند داشت، به این معنی که گزاره شرطی متناظر نمیتواند نادرست باشد. بنابراین، اگر یک صورت استدلال معتبر باشد، گزاره شرطی متناظر آن باید یک توتولوژی باشد.
رابطه مهم بین یک صورت استدلال (یا استدلال) و عبارت-گزارهای شرطی متناظر آن میتواند بوسیله جداول ارزش آشکاری یاید. صورت استدلال بالا و عبارت-گزارهای متناظر آن در جدول ارزش زیر آمده است.
| p۲ | ∴ | p۱ | مقدم | تالی | شرطی |
| p | q | p ⊃ q | (p ⊃ p) • q | q | [(p ⊃ q) • p] ⊃ q) |
| T | T | T | T | T | T |
| T | F | F | F | F | T |
| F | T | T | F | T | T |
| F | F | T | F | F | T |
در این جدول ارزش میتوان دید که دو مقدمه فقط در سطر ۱ هر دو درست هستند، وقتی که p درست و q درست است. در این ترکیب مقادیر ارزش برای متغیرهای گزارهای p و q، هر دو مقدمه درست هستند و نتیجه نیز درست است. بنابراین، این صورت استدلال معتبر است زیرا نمیتواند دارای همه مقدمات درست و نتیجه نادرست باشد.
عبارت-گزارهای شرطی که با صورت استدلال تناظر دارد در آخرین ستون جدول ارزش قرار دارد. از آنجایی که یک گزاره شرطی تنها در صورتی نادرست است که مقدم آن درست و تالی آن نادرست باشد، این گزاره شرطی تنها وقتی نادرست بود که مقدم آن، یعنی (p⊃q)•p (یعنی عطف دو مقدمه استدلال) درست و تالی آن، یعنی گزاره q (یعنی نتیجه استدلال)، نادرست بود. همانطور که آشکارا میتوان دید، در هر چهار ترکیب مقادیر ارزش برای متغیرهای گزارهای p و q (یعنی در هر چهار سطر)، هیچ حالتی نیست که مقدمات همه درست و نتیجه نادرست باشد. به همین ترتیب، ستون چهارم و پنجم نشان میدهند که هیچ حالتی نیست که مقدم شرط (ستون ۴) درست و تالی (ستون ۵) نادرست باشد. به همین دلیل گزاره شرطی (ستون ۶) در هر چهار حالت درست است. گزاره شرطی نمیتواند نادرست باشد - نمیتواند یک مقدم درست و یک تالی نادرست داشته باشد - زیرا صورت استدلال نمیتواند همه مقدمات درست و یک نتیجه نادرست را داشته باشد (یعنی چون صورت استدلال معتبر است). این نشان میدهد که صورت استدلال اگر و تنها اگر معتبر است که گزاره شرطی متناظر یک توتولوژی باشد.➥
توجه داریم که برای هر صورت استدلال نامعتبر از نوع تابع-ارزشی، عبارت-گزارهای شرطی متناظر یک توتولوژی نخواهد بود. عبارت-گزارهای که عطف مقدمات آن دربردار نتیجه آن است، برای یک استدلال نامعتبر، یا ممکن یا تناقض خواهد بود.➥ برای مشاهده این، صورت استدلال نامعتبر زیر موسوم به وضع تالی را در نظر بگیرید:
p۱: p ⊃ q
p۲: q
∴ p
جدول ارزش این صورت استدلالی و شرطی متناظر آن به قرار زیر است.
| ∴ | p۲ | p۱ | مقدم | تالی | شرطی |
| p | q | p ⊃ q | (p ⊃ q) • q | p | [(p ⊃ q)•q] ⊃ p) |
| T | T | T | T | T | T |
| T | F | F | F | T | T |
| F | T | T | T | F | F |
| F | F | T | F | F | T |
همانطور که جدول ارزش نشان میدهد، دو ترکیب از مقادیر ارزش برای متغیرهای گزارهای این صورت استدلال وجود دارد که در آن هر دو مقدمه درست هستند. در سطر ۱، وقتی p درست است و q درست است، هر دو مقدمه درست هستند و نتیجه نیز درست است. در این مورد خاص، مقدم (ستون ۴) و تالی (ستون ۵) درست است و بنابراین گزاره شرطی مربوط (ستون ۶) درست است. با این حال، در سطر ۳، دو مقدمه هر دو درست است و نتیجه نادرست است، که نشان میدهد صورت استدلال نامعتبر است زیرا میتواند همه مقدمات درست و نتیجه نادرست را داشته باشد. بیاعتباری این صورت استدلال گویای این واقعیت است که گزاره شرطی مربوط در آن مورد خاص نادرست است (سطر ۳)، زیرا در آن صورت، مقدم آن (ستون ۴) درست و تالی آن (ستون ۵) نادرست است. گزاره شرطی یک توتولوژی نیست، بلکه ممکن است، و بنابراین صورت استدلال مربوط نامعتبر است. عبارت-گزارهای شرطی یک ممکن است زیرا میتواند نادرست باشد (سطر ۳) و میتواند درست باشد (سطر ۱، ۲ و ۴). شرطی میتواند نادرست باشد زیرا میتواند یک مقدم درست و یک تالی نادرست داشته باشد (سطر ۳)؛ این ممکن است زیرا این صورت استدلال نامعتبر میتواند همه مقدمات درست و یک نتیجه نادرست را داشته باشد، همانطور که در واقع در سطر ۳ وجود دارد، زمانی که p نادرست و q درست است.
این واقعیت که یک صورت استدلال معتبر است اگر و تنها اگر شرطی متناظر آن یک توتولوژی باشد، در توضیح و موجه بودن برهان شرطی که در قسمت برهان شرطی خواهد آمد مهم است.
تمرین
الف- برای هریک از گزارههای زیر که در سمت چپ آمدهاند، نشان دهید مورد جانشین کدام صورت گزارهای در سمت راست، در صورت وجود، هستند، و نیز نشان دهید کدام، در صورت وجود، صورت نوعی گزاره دادهشده است.
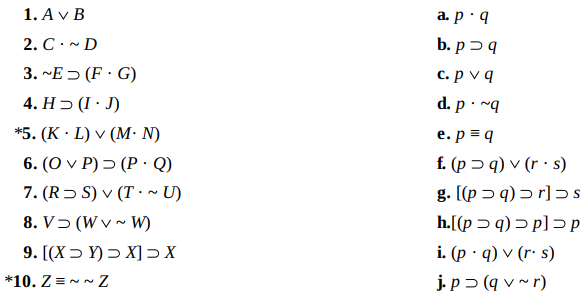
ب- با کاربرد جدول ارزش، هریک از صورتهای گزارهای زیر را بهعنوان توتولوژی، تناقض و ممکن متمایز نمایید.
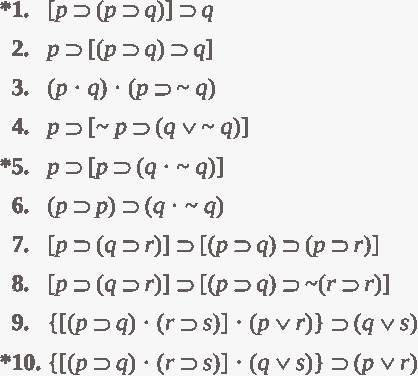
ج- با کاربرد جدول ارزش معین کنید کدامیک از دو شرطیهای زیر توتولوژی هستند.


