منطق جدید و زبان نمادین آن

برای فهم استدلال استنتاجی نیازمند به یک نظریه عام استنتاج‌ هستیم. یک نظریه بزرگ استنتاج دارای دو هدف به قرار زیر است:

نماد، تاروپود همه اندیشه و همه پژوهش است، زیستِ اندیشه و دانش درون نشانه‌ها است، نادرست است فقط بگوییم داشتن زبان خوب برای اندیشگی خوب مهم است، بلكه گوهر هستی آن است.

چارلز سندرس پیرس

برای پرهیز از کاستی‌های زبان طبیعی در تحلیل منطقی، ابتدا نیاز است برگردانی به نشان‌گذاری دقیق‌تر را داشت.

آلونزو چرچ

دو نظریه بزرگ منطقی در نیل بدین مقصود به کنکاش پرداخته‌اند. اولی آن‌ها موسوم به منطق "کلاسیک" (یا منطق ارسطویی) است که در فصل های ۶ تا ۸ بررسی گردید. دومی که موسوم به منطق جدید (نیز منطق نمادین، یا منطق ریاضی) است موضوع این و دو فصل بعد خواهد خواهد بود.

گرچه این دو بدنه بزرگ اهداف مشابه دارند، ولی آنها را به روش‌های بسیار متفاوت پیش می‌برند. منطق جدید بر پایه دستگاه قیاس‌ها بنا نشده است و با تحلیل گزاره‌های حملی آغاز نمی‌شود. منطق جدید نیز، گرچه آن را با مفاهیم و روش‌های بسیار متفاوت انجام می‌دهد، در پی تمیز استدلال معتبر از نامعتبر است. بنابراین، ما باید در ادامه مسیر از نو آغاز کنیم و دستگاه منطقی جدیدی را گسترش دهیم که با برخی موضوعات بسیار یکسان با آنچه در منطق قدیم بررسی‌شده سروکار داشته باشد— و این کار را نیز حتی با کارآمدی بیشتر انجام دهد.

منطق جدید ابتدا به مشخص کردن پیوند (رابط)‌ هایی می‌پردازد که استدلال استنتاجی وابسته به آن‌هاست. سپس، با کاربرد این پیوند‌‌ ها یک توصیف عام ازاین‌گونه استدلال‌ها و نیز گسترش روش‌های آزمون اعتبار آن‌ها ارائه می‌دهد.

نمادها اندیشیدن درباره استدلال‌ها را بسیار آسان می‌کند. آن‌ها ما را توانا می‌سازند تا به قلب یک استدلال دست‌یافته و سرشت اصلی آن را نشان داده، سپس آنچه را که مدخلیت در خود استدلال ندارد به کنار نهاده. بعلاوه، با استفاده از نماد می‌توان بعضی اعمال منطقی را توسط ماشین انجام داد که در غیر این صورت می‌توانست نیازمند به تلاش بسیار زیاد باشد. به‌ظاهر تناقض‌آمیز می‌آید، اما چنین است که یک زبان نمادین می‌تواند کمک کند تا بعضی فعالیت‌های فکری را بدون نیاز به فکر زیاد انجام داد.

ارقام هندی-عربی (1، 2، 3، ...) که امروز آن‌ها را بکار می‌بریم، سودمندی یک زبان نمادین بهبودیافته را به نمایش می‌گذارند. آن‌ها جایگزین ارقام رومی (III, II, I, . . .) شده‌اند که کار با آنان بسیار پرزحمت بود. ضرب ۱۳ در ۹ البته اکنون آسان است؛ ولی ضرب CXIII در IX هرگز چنین آسان نیست. حتی رومیان تحصیل‌کرده مجبور بودند راهی برای کارآمدی این سبک نمادگذاری اعداد بیابند*.

منطق‌ دانان کلاسیک ارزش فراوان نماد و استفاده از آن در تحلیل را می‌فهمیدند. ارسطو از نماد از نماد بعنوان متغیر در تحلیل‌های خود سود می‌برد از نماد بعنوان متغیر در تحلیل‌های خود سود می‌برد، و سیستم پالوده قیاس‌های ارسطویی، همان‌طور که در فصل‌های قبل نشان داده‌ شد، به روش‌های بسیار آگاهانه از نماد بهره می‌برد. اما بیشتر پیشرفت‌های انجام یافته در تدبیر و کاربرد مؤثرتر نماد در منطق، به‌طور عمده در قرن بیستم شکل گرفته است.

نمادگذاری مدرن که با آن استنتاج تحلیل می‌شود، از بنیاد متفاوت از روش‌های کلاسیک است. روابط بین طبقه‌های اشیاء آن‌گونه که در ارسطو و پیروان وی بود دیگر نزد منطقیان جدید مرکزیت ندارد. بجای آن، نگاه منطق‌دان امروز به ساختار درونی گزاره‌ها و استدلال همراه با رابط‌های منطقی — بسیار اندک — است؛ پیوندهایی که نقش تعیین‌کننده در همه استدلال‌های استنتاجی دارند. بنابراین منطق جدید برخلاف منطق ارسطویی دست و پاگیر نیست؛ آن‌گونه که در منطق ارسطویی نیاز بود استدلال‌های استنتاجی به صورت‌های قیاسی تبدیل شوند، کاری اغلب پرزحمت که در فصل قبل شرح آن آمد.

سیستم منطق جدید که هم اکنون بر آنیم تا به کاوش آن پرداخته، به طریقی کمتر از تحلیل قیاسی مجلل؛ اما بسیار تواناتر است. شکل‌هایی از استدلال‌های استنتاجی وجود دارند که قیاس‌ها نمی‌توانند به نیکویی به آن‌ها بپردازند. با کاربرد روش‌های منطق جدید، و زبان نمادین قابل‌ انعطاف آن، قادر خواهیم‌ شد تا به‌طور مستقیم اهداف تحلیل استنتاجی را پیگیری کنیم و نیز به فهم ژرف‌تر دست‌یابیم. نماد‌های منطقی، که اکنون در پی کاوش آن‌ها هستیم، دستیابی کامل‌تر و کارآمدتر ما را به هدف محوری منطق استنتاجی، که همانا تمیز استدلال‌های نامعتبر از معتبر است، میسر میسازد.

پانوشت:

[*]-

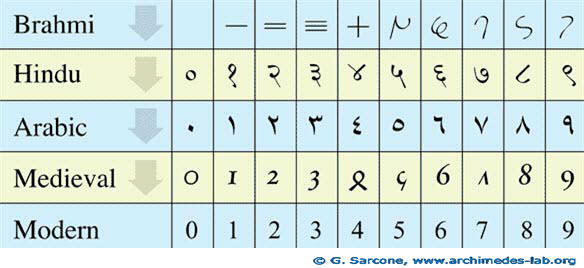
[این ارقام در هند و قبل از اسلام بکار می‌رفت. خوارزمی (۸۵۰-۷۸۰م) از آنان برای اعمال ریاضی سود جست (رساله "جمع و تفریق با ارقام هندی") و کار برد آن‌ها در شرق عالم اسلامی آن روزگار (ایران) رایج گشت. این نمادها در گذر و رسیدن به غرب عالم اسلامی (مراکش امروز و در طی چند صدسال) تغییر شکل دادند (برای مثال ۲ به 2 و مثل آن). در همان‌جا و توسط فیبوناچی (۱۲۵۰-۱۱۷۰م) ریاضیدان ایتالیایی این نمایش ارقام و فن محاسبه با آنها در اروپا نیز رایج شد. __توضیح از برگرداننده.]