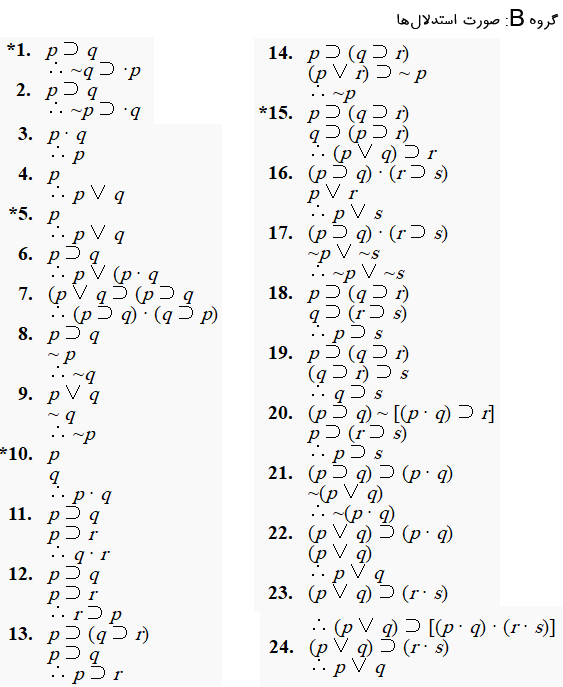صورت استدلال و وازنش با همسنجی (قیاس تشبیهی)
منطق گزارهای و گزارههای تابع-ارزش
درآمد به منطق فصل ۹ قسمت ۴
درقسمتهای قبلِ این فصل در معرفی زبان نمادین منطق گزارهها از نقش رابطهای منطقی تابع-ارزشی عطف •، نقض ~، فصل ⋁ و شرط ⊂ در این زبان نیز گفته شد. در قسمت یکم بویژه از مفهوم "صورت" و اهمیت آن در منطق مدرن صحبت به میان آمد. در این قسمت و در این رابطه با دو مفهوم متغیر و صورت استدلال روبرو میشویم.
۴.۹ صورت استدلال و وازنش با همسنجی (قیاس تشبیهی)
وازنش با همسنجی
ابطال با قیاس تشبیهی
تبکیت منطقی
Refutation by Analogy
روشی است (استدلالی است) برای نشان دادن خطای یک استدلال با آوردن استدلالی دیگر با همان صورت که آشکارا دانسته است مقدمات آن درست و نتیجه آن نادرست است.
متغیر گزارهای
حروف گزارهای
متغیر
Statement variable
Statement letter
Variable
جایبان؛ یک حرف (طبق قرارداد، هر یک از حروف کوچک آغازشده با q, p و غیره) که ممکن است یک عبارت گزارهای جایگزین آن شود.
صورت استدلال
Argument Form
آرایهای از نمادها است که ساختار استدلال را بازمینمایاند و شامل متغیرهای گزارهای و نه گزاره است.
مورد جانشین صورت استدلالی
Substitution Instance of an Argumentm
هر استدلال که با جانشینی سازگار گزاره ها بجای متغیرهای گزارهای در آن صورت استدلال حاصل شده باشد.
صورت نوعی
Specific form
هر استدلال که با جانشینی سازگار گزارهها بجای متغیرهای گزارهای در آن صورت استدلال حاصل شده باشد.
وظیفه منطق استنتاجی تمیز استدلال معتبر از نامعتبر است. اگر مقدمات یک استدلال معتبر درست باشند (که در فصل یکم توضیح داده شد)، نتیجه آن نیز باید درست باشد؛ و اگر نتیجه یک استدلال نامعتبر نادرست باشد، حداقل یکی از مقدمات آن نیز باید نادرست باشد.
اکنون میخواهیم این بیان توصیفی از اعتبار را دقیقتر بیان کرده و برای این کار مفهوم صورت استدلال را به میان میآوریم. به دو استدلال زیر توجه نمایید که چگونه دارای صورت منطقی یکسان هستند. فرض کنید ابتدا با اولین استدلال از این دو به شرح زیر روبرو شدهایم:
اگر بیکن نمایشنامههای منتسب به شکسپیر را نوشته باشد، آنگاه بیکن یک نویسنده بزرگ است.
بیکن یک نویسنده بزرگ است.
بنابراین بیکن نمایشنامههای منتسب به شکسپیر را نوشته است.
میتوانیم با مقدمات این استدلال موافق ولی با نتیجه مخالف باشیم و استدلال را نامعتبر برآوُرد کنیم. یک روش برای اثبات نامعتبر بودن استدلال استفاده از روش قیاس تشبیهی (همسنجی / آنالوجی) است. میتوان به آورنده استدلال جواب متقابل داده و بگوییم:
اگر جرج واشنگتن را ترور کرده باشند، آنگاه جرج واشنگتن مرده است.
جرج واشنگتن مرده است.
بنابراین جرج واشنگتن ترور شده است.
حالا دیگر نمیتوان بهطورجدی از این استدلال دفاع کرد، و ادامه میدهیم، «چون میدانیم مقدمات درست هستند و بعلاوه میدانیم نتیجه نادرست است، این استدلال آشکارا نامعتبر است؛ استدلال شما نیز دارای صورت یکسان با این استدلال است، بنابراین آن نیز نامعتبر است». این طریق وازنش بسیار مؤثر است.
این روش یعنی وازنش با قیاس تشبیهی (وازنش با همسنجی) راهگشا به سمت یک تکنیک عام برای آزمون استدلال است. برای ثابت کردن بیاعتباری یک استدلال کافی است تا یک استدلال دیگر را پیکربندی کرد، به قسمی که:
۱- دقیقاً بهصورت استدلال اول باشد؛
۲- و دارای مقدمات درست و نتیجه نادرست باشد.
این روش بر اساس این واقعیت است که اعتبار و بیاعتباری یک استدلال بهطور محض یک ویژگی صوری است، آنطورکه میتوان گفت: دو استدلال با صورت دقیقاً یکسان هر دو معتبر یا هر دو نامعتبر هستند؛ و این فارغ از آنکه در رابطه با چه موضوعات مختلفی باشند است. فرض ما اینجا این است که گزارههای سادهی داخل در استدلال، نه منطقاً درست هستند (مثل، همه صندلیها صندلی هستند) و نه منطقاً نادرست هستند (مثل، بعضی صندلیها غیر-صندلی هستند.) همچنین فرض کرده که روابط منطقی بین گزارههای ساده داخل در استدلال، آنهایی هستند که توسط مقدمات ضمانت یا بیانشدهاند. نکته موجود در این محدودیتها آن است که در این فصل و فصل بعد ملاحظات خود را صرفاً به استدلالهای تابع-ارزشی (استدلالی که مقدمات و نتیجه آن گزارههای تابع-ارزش باشند) محدود نماییم، و گونههای دیگر استدلال که اعتبار آنها منوط به ملاحظات منطقی پیچیدهتر است و اکنون جای عنوان کردن آنها نیست، را استثناء نماییم.
وقتی در یک استدلال گزارههای ساده را بهصورت خلاصه شده با حروف بزرگ نمایش دهیم، آنگاه صورت منطقی آن استدلال بهطور واضح نشانداده میشود. بنابراین میتوان گزارههای "بیکن نمایشنامههای منسوب به شکسپیر را نوشته است"، "بیکن یک نویسنده بزرگ بود"، "جرج واشنگتن ترور شده است"، "جرج واشنگتن مرده است" را به ترتیب با حروف A, G, B و D نشان داد و نماد ∴ را نیز را برای "بنابراین" در نظر گرفت، سپس دو استدلال قبلی را به شیوه زیر نمادین کرد:
| B ⊃ G | A ⊃ D | |
| G | و | D |
| ∴B | ∴A |
اکنون صورت یکسان آنها به آسانی دیده میشود.
برای آنکه بتوانیم درباره صورت یک استدلال بجای یک استدلال خاص بحث نماییم، نیازمند به روشی هستیم تا خود صورت استدلال را نمادین کنیم. برای این کار مفهوم "متغیر" را معرفی میکنیم. در قسمت قبل، از حروف بزرگ استفاده کردیم تا گزارههای خاص و ساده را نمادین کنیم. برای جلوگیری از اشتباه و ابهام، حروف کوچک از میانه الفبای انگلیسی، یعنی s, r, q, p , . . . را بهعنوان متغیرهای گزارهای (همچنین "متغیر" یا "حروف گزارهای") بکار میبریم. یک متغیر گزارهای، آنگونه که ما آن را بکار خواهیم برد، صرفاً یک حرف است که برای آن یا بجای آن یک گزاره میتواند جانشین شود. گزارههای مرکب و نیز گزارههای ساده میتوانند جانشین متغیرهای گزارهای شوند.
اکنون، صورت استدلال را اینگونه تعریف کرده که عبارت است از آرایهای از نمادها شامل متغیرهای گزارهای و نه گزاره، به قسمی که هرگاه گزارهها— یک گزاره یکسان برای همه موارد یک متغیر گزارهای یکسان— جانشین متغیرهای گزارهای شوند، آنگاه نتیجه یک استدلال باشد. برای محکمکاری، چنین قرار میگذاریم که در هر صورت استدلالی: p اولین رویداد یک متغیر گزارهای باشد، q دومین رویداد، r سومین رویداد و الیآخر. بنابراین، عبارت:
| p ⊃ q |
| q |
| ∴p |
یک صورت استدلالی است، که هرگاه گزارههای B و G را به ترتیب جانشین متغیرهای گزارهای p و q نماییم، آنگاه آنچه حاصل میگردد عبارت از نتیجه اولین استدلالی است که در این قسمت آورده شد. اگر گزارههای A و D برای متغیرهای گزارهای p و q جانشین شوند، آنگاه نتیجه عبارت از دومین استدلال خواهد بود. هر استدلالی که از جانشینی متغیرهای گزارهای با گزارهها به دست آید را یک مورد جانشین آن صورت استدلالی نامیده. میتوان در باره هر مورد جانشینی یک صورت استدلال گفت که دارای آن صورت است و نیز هر استدلال که دارای یک صورت معلوم است مورد جانشین آن صورت معلوم است.
برای هر استدلال معمولاً چندین صورت استدلال وجود دارد که استدلال داده شده همچون یک مورد جانشین برای همه آنهاست. برای مثال اولین استدلال این قسمت:
| B ⊃ G |
| G |
| ∴B |
یک مورد جانشین برای هر یک از چهار صورت استدلال زیر است:
| p | p ⊃q | p⊃q | p ⊃q |
| q | r | r | q |
| ∴r | ∴s | ∴p | ∴p |
استدلال دادهشده را میتوان با جانشینی B برای p و G برای q در صورت استدلالی اول؛ جانشینی B برای p و G برای جانشینی برای هم q و هم r در صورت استدلالی دوم؛ B برای هم p و هم برای s و G برای هم q و هم برای r در صورت استدلالی سوم؛ B⊃G برای q، و B برای r در صورت استدلالی چهارم به دست آورد. از این چهار صورت استدلال، اولی تناظر نزدیکتری با استدلال دادهشده دارد تا بقیه. این ازآنجهت است که استدلال دادهشده حاصل آن صورت استدلال اول است که از جانشینی یک گزاره ساده متفاوت برای هر متغیر گزارهای متمایز در آن به دست آمده. صورت استدلالی اولی را صورت نوعی استدلال دادهشده نامیده. تعریف ما از صورت نوعی یک استدلال دادهشده عبارت است از: هرگاه یک استدلال بهوسیله جانشینی یکنواخت یک گزاره ساده متفاوت برای هر متغیر گزارهای در یک صورت استدلال حاصل شده باشد، آنگاه به این صورت استدلال صورت نوعی آن استدلال گفته. برای هر استدلال دادهشده یک صورت استدلال یکتا که صورت نوعی آن است وجود دارد.
تمرین
در زیر یک گروه استدلال (گروه A از a تا o) و یک گروه صورت استدلال (گروه B از شماره ۱ تا ۲۴) آمده است.
برای هریک از استدلالها(در گروه A) نشان دهید، در صورت وجود، مورد جانشینی کدام صورت استدلالی (در گروه B) است.
بعلاوه برای هر استدلال (در گروه A) نشان دهید، کدام صورت استدلال (در گروه B) در صورت وجود صورت نوعی آن استدلال است.
مثال:
استدلال a در گروه A: پس از بررسی تمامصورتهای استدلالی در گروه B، درمیابیم که این استدلال فقط مورد جانشین شماره ۳ است. بعلاوه شماره ۳ صورت نوعی این استدلال نیز هست.
استدلال j در گروه A: با بررسی صورتهای استدلال در گروه B، درمیابیم که استدلال j مورد جانشین شماره ۶ و همینطور شماره ۲۳ است. اما فقط شماره ۲۳ صورت نوعی استدلال j است.
استدلال m در گروه A: با بررسی همه صورتهای استدلال در گروه B، درمییابیم که استدلال m در گروه A جانشین شماره ۳ و شماره ۲۴ است. اما هیچ صورت استدلال در گروه B نیست که صورت نوعی استدلال m باشد.
استدلال e در گروه A:صورت نوعی ۱۰ است .
صورت ۳ در گروه B دارای مورد جانشین o در گرو B و نیز صورت نوعی Bهم است.