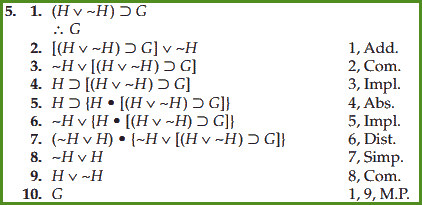ساختن برهان صوری با نوزده قاعده استنتاج
روشهای استنتاج
درآمد به منطق فصل ۱۰ قسمت ۸
در قسمت پیشین دستگاه استنتاج طبیعی همراه ۱۹ قاعده استنتاج به شمول مفاهیم مهمی همچون افزونگی، تمامیت قواعد استنتاج و تصمیم پذیری در دستگاه استنتاج طبیعی معرفی شد. این قسمت روند ساخت برهان در دستگاه استنتاج طبیعی با مثالهای راه گشا و کار بستن ۱۹ قاعده استنتاج پی میگیرد.
۸.۱۰ ساختن برهان صوری با نوزده قاعده استنتاج
در دست داشتن مجموعهای از ۱۹ قاعده استنتاج بجای فقط نه قاعده، برای انتخاب ساختن برهانهای صوری را اندازهای پیچیدهتر میکند. گرچه هدف یکسان است (یعنی همان که در قسمتهای ۴ و ۵ این فصل پیگیر آن بودیم)، لیکن روند تدبیر برهان متضمن جستجو در جعبهابزار ذهنی طولانیتری خواهد بود. این زنجیره منطقی ناگسسته که به تدبیر و تدوین میپردازیم سرانجام به نتیجه میرسد، آنگونه که هر گام با یک صورت استدلال معتبر مقدماتی یا یک همارزی منطقی موجه خواهند شد. هر استدلال دادهشده میتواند از هر دو قسم قاعده بکار گیرد. تعادل و ترتیب آنها بوسیله نیاز منطقی مواجهشده حین پیادهسازی استراتژی، یک استراتژی که منجر به فرجام برهان خواهد شد، معین میشود.
آنچه به دنبال میآید مجموعهای از برهانهای صوری بینقص است، که هرکدام بر قواعدی از هر دو نوع برپای گردیده. به خاطر آشنایی با کار زدن مجموعه کامل قواعد، ما هر یک از این برهان را بررسی خواهیم کرد تا ببینیم چه قاعدهای برای موجهسازی هر گام از برهان به کار بسته شده.
مثال ۱
۱. A ⊃ B
۲. C ⊃ ~B
∴ A ⊃ ~C
۳. ~~B ⊃ ~C
۴. B ⊃ ~C
۵. A ⊃ ~C
حل بعد از دیدن مرور کلی.
| قواعد استنتاج ۱: صورتهای استدلال معتبر مقدماتی | ||||
| قواعدی که امکان استنتاج معتبر از گزارههایی که بهعنوان مقدمه مفروضاند را ممکن میسازند. | ||||
| صورت | نام انگلیسی | کوته سازی | نام | شماره |
| p⊃q p ∴ q | Modus Ponens | M.P. | قیاس استثنائی | ۱. |
| p⊃q ~q ∴ ~p | Modus Tollens | M.T. | قیاس اقترانی | ۲. |
| p⊃q q⊃r ∴ p ⊃ r | Hypothetical Syllogism | H.S. | قیاس شرطی | ۳. |
| p∨q ~q ∴p | Disjunctive Syllogism | D.S. | قیاس فصلی | ۴. |
| (p⊃q)•(r⊃s) p∨r ∴ q ∨ s | Constructive Dilemma | C.D. | دو لِمّی ساختی | ۵. |
| p⊃q ∴ p⊃(p•q) | Absorption | Abs. | جذب [گیرایش] | ۶. |
| p•q ∴ p | Simplification | Simp. | ساده گردانی | ۷. |
| p q ∴ p • q | Conjunction | Conj. | پیوست | ۸. |
| p ∴ p ∨ q | Addition | Add. | افزایش | ۹. |
| قواعد استنتاج ۲: همارزیهای منطقی هریک از عبارتهای همارز منطقی زیر میتوانند جایگزین هر عبارت گزارهای رویدادهای هرچه که باشد گردند. | ||||
~(p•q)  (~p∨~q) | De Morgan’s Theorems | .DeM | قضیههای دمورگان | ۱۰. |
~(p∨q) (~p•~q) | ||||
(p∨q) (q∨p) | Commutation | .Com | جابجایی | ۱۱. |
(p•q) (q•p) | ||||
[(p•q)•r] [p•(q•r)] | Association | .Assoc | انجمنی | ۱۲. |
[(p∨q)∨r] [p∨(q∨r)] | ||||
[p•(q∨r)] [(p•q)∨(p•r)] | Distribution | .Dist | پخش پذیری | ۱۳. |
[p∨(q•r)] [(p∨q)•(p∨r)] | ||||
p  ~~p ~~p | Double Negation | .D.N | نقض دوگانه | ۱۴. |
p⊃q ~q⊃~p | Transposition | .Trans | ترانهش /عکس نقیض | ۱۵. |
(p⊃q) (~q ∨ p) | Material Implication | .Impl | استلزام مادی | ۱۶. |
(p≡q) [(p •q) ∨ (~p • ~q)] | Material Equivalence | .Equiv | همارزی مادی | ۱۷. |
(p≡q ) [(p⊃q)∨(p ⊃q)] | ||||
[(p •q)⊃r] [p⊃(q⊃r)] | Exportation | .Exp | واگردان | ۱۸. |
p  (p∨p) (p∨p) | Tautology | .Taut | توتولوژی | ۱۹. |
p  (p • p) (p • p) | ||||
حل مثال ۱:
مثال ۲
۱. (D • E) ⊃ F
۲. (D ⊃ F) ⊃ G /∴ E⊃ G
۳. (E • D) ⊃ F
۴. E ⊃ (D ⊃ F)
۵. E ⊃ G
حل
خط ۳ فقط (D • E) را جابجا کرده؛ مینویسیم:
۱, .Com
خط ۴ خط ۳ را واگردانده؛ مینویسیم:
۳, .Exp
خط ۵ قیاس شرطی را به خط ۴ و ۲ بکار بسته؛ مینویسیم:
۴, ۲, H.S.
توجه: بعد از تمرین متن ادامه دارد.
تمرین
(آ) در هریک از استدلالهای صوری زیر برای هر خط که مقدمه نیست، قاعده استنتاجی که آن را موجه میکند بنویسید.

حال با استفاده از مجموعه کامل قواعد استنتاج سراغ ساختن برهانهای صوری میرویم. در آغاز به استدلالهای ساده که برهان آنها فقط به دو عبارت گزارهای بیشتر از مقدمات خود نیاز دارد میپردازیم. هریک از خطهای میتوانند با یکی از صور استدلالهای مقدماتی معتبر یا قواعد جایگزینی توجیه شوند. با دو مثال، دو تمرین اول مجموعه (ب) که بلافاصله به دنبال خواهد آمد، ادامه میدهیم.
مثال۱
۱. A ⊃ ~A
∴ ~A
حل
آشکار است که برهان این استدلال در اولین گام باید با یک مقدمه تک روبرو شود. چه میتوان کرد تا سودمند باشد؟ اگر استلزام مادی را بکار بندیم عبارت-گزارهای A∨~A~ را به دست میآوریم که بعد میتوان صورت استدلال معتبر توتولوژی را به آن بکار بست، و آنوقت حاصل کار همان است که به دنبال آنیم. بنابراین برهان، آنچه در زیر آمده خواهد بود.
۱. A⊃ ~A
∴ ~A
۲. ~A ∨ ~A ۱, Impl.
۳. ~A ۲, Taut.
مثال ۲
۱. B • (C • D)
∴ C • (D • B)
حل
در این برهان نیاز است فقط گزارهها باز چیده شوند. در گام اول میتوان ترکیب عطفی اصلی مقدمه یکم را جابجا کرد که حاصل آن C•D)•B) خواهد شد. سپس باقیمیماند تا فقط سه گزاره را بوسیله انجمنی (.Assoc) گروهبندی دوباره کنیم. بنابراین برهان آنچه در پی میآید است.
| ۱. B • (C • D) ∴ C • (D • B) ۲. (C • D) • B ۳. C • (D • B) | ۱, Com. ۲, Assoc. |
در این برهان، مثل همه برهانهای صوری، آخرین خط از دنبالهای ساختهشده همان نتیجهای است که در پی استنتاج آن آنیم.
توجه: بعد از تمرین متن ادامه دارد.
تمرین
(ب) در هریک از تمرینات زیر افزودن فقط دو عبارت گزارهای به مقدمات، یک برهان صوری برای اعتبار آن به دست خواهد داد. برای هریک از استدلالهای زیر یک برهان صوری اعتبار بسازید.
در برهانهای صوری زیر و همه برهانهایی که بعداً در این قسمت میآیند، در سمت راست هر خط آنها قاعده استنتاجی که آن خط برهان را توجیه میکند بنویسید. بسیار راحتتر است اگر ابتدا شماره خط (یا خطها) بهکاررفته و سپس نام قاعده استنتاج کار زدهشده به آن شماره خطها (کوتهسازیشده)نوشته شود .
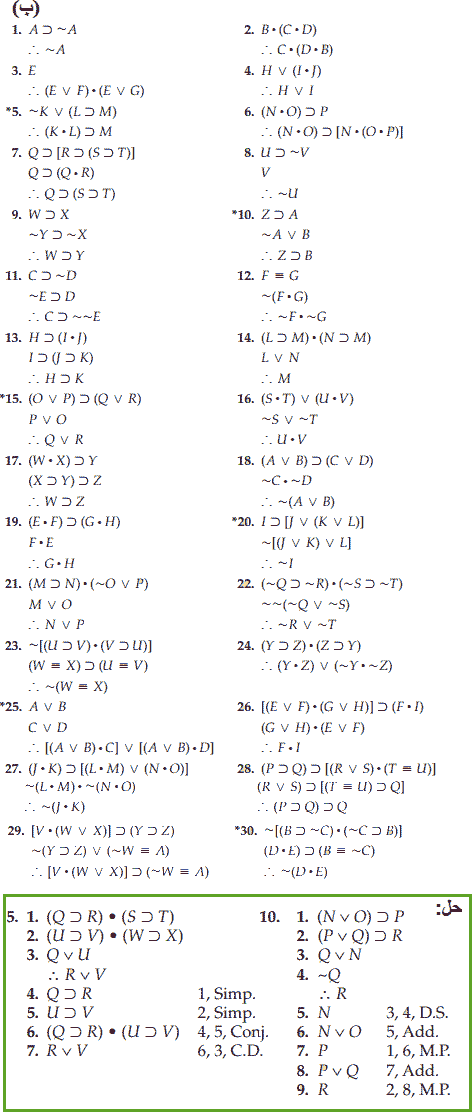
همانطور که به سمت برهانهای صوری نیازمند به سه خط افزوده به مقدمات پیش میرویم، تدوین یک استراتژی برای تعیین دنباله موردنیاز دارای اهمیت میگردد. بیشتر چنین استدلالها همچنان ساده خواهند بود، اما گاهی مسیر برهان میتواند کمتر آشکار باشد. اینجا را نیز با دو مثال آغاز میکنیم، دو تمرین اول مجموعه (ج) که بعد از مثالها آمده.
مثال ۱
۱. ~A ⊃ A
∴ A
حل
برای آغاز فقط یک مقدمه در اختیارداریم. در بیشتر موارد برگردان گزارههای شرطی به گزارههای ترکیب فصلی نتیجهبخش است. اگر این کار را با خط ۱ (با کار زدن .Imp) انجام دهیم A~~ بهعنوان فصل اول به دست خواهد آمد؛ این مؤلفه را میتوان بهراحتی با A جایگزین کرد؛ و سپس کار زدن صورت استدلال توتولوژی آنچه را که در پیاش بودیم به ما خواهد داد. این برهان بهقرار زیر است:
| ۱. ~A ⊃ A ∴ A ۲. ~~A ∨ A ۳. A ∨ A ۴. A | ۱, Impl. ۲, D.N. ۲, Taut. |
مثال ۲
۱. ~B ∨(C • D )
∴B ⊃ C
حل
در تنها مقدمه این استدلال گزاره D وجود دارد. ما به دنبال برهانی هستیم که نتیجه آن B⊃C است، و بنابراین باید به روشی D را حذف کنیم. چگونه میتوان این کار را کرد؟ میتوانیم عبارت-گزارهای C•D را با پخش A~ در آن از هم بگسلانیم. پخشپذیری دریکی از گونههایش میگوید:
[p ∨ (q • r)] ![]() [(p ∨ q)•(p ∨ r)].
[(p ∨ q)•(p ∨ r)].
آن را که به خط ۱ به کاربندیم، حاصل این جایگزینی عبارت-گزارهای:
(B ∨ C)•(~B ∨ D~)
است.
این دو، عبارات بههمپیوسته هستند، بنابراین با ساده گردانی میتوان (B∨C~) را بیرون آورد. و سپس با کار زدن .Impl این عبارت-گزارهای را با B⊃C جایگزین کرد که همان نتیجه مطلوب ماست. برهان بهقرار زیر است:
| ۱. ~B ∨ (C • D ) ∴ B ⊃ C ۲. (~B ∨ C) • (~B ∨ D) ۳. ~B ∨ C ۴. B ⊃ C | ۱, Dist. ۲, Simp. ۳, Impl. |
توجه: بعد از تمرین متن ادامه دارد.
تمرین
(ج) در هر یک از تمرینات زیر افزودن فقط سه عبارت گزارهای به مقدمات، یک برهان صوری برای اعتبار آن به دست خواهد داد. برای هریک از آنها یک برهان صوری بسازید.

برهانهای صوری گاهی نیازمند به گامها یا خطهای زیاد در دنباله هستند. ما بتدریج درمییابیم به تکرار با الگوهای معینی از استنتاج در استدلالهای طولانی مواجه خواهیم شد. بنابراین، عاقلانه است تا با این الگوهای تکرار شدنی آشنا شویم.
این را میتوان بهخوبی بوسیله دو تمرین اول مجموعه (د) که به دنبال میآید نشان داد. ابتدا فرض کنید که میدانیم گزاره دادهشده A نادرست است. ممکن است در مرحله بعدی برهان نیاز باشد ثابت کنیم گزاره دیگری، به فرض B، مستلزم درستی آن گزاره است که میدانیم نادرست است. این را میتوان بهآسانی ثابتکرد و اینچنین الگو غیرمعمول نیست. بهعبارتدیگر و به گونه صوری، چگونه میتوان A⊃B را از A~ استنتاج کرد؟ این را کنون خواهیم دید:
مثال ۱
۱. ~A ⊃ A
∴ A
حل
اگر بدانیم A~ درست است، مانند این مثال، پس A باید نادرست باشد. یک گزاره نادرست بطور مادی مستلزم هر گزاره دیگری است. بنابراین B⊃A، برای هر چه B مدعی آن باشد، وقتی میدانیم A~ درست است، باید درست باشد. در این حالت A~ بهعنوان مقدمه دادهشده؛ آنچه نیاز است افزودن B دلخواه به آن و سپس کار زدن استلزام مادی است. برهان صوری این استدلال (یا قطعه برهان [ برهان محاطی / زیر برهان / برهانک / برهان فرعی، وقتیکه بخشی از یک برهان طولانیتر است) بهقرار زیر است.
| ۱. ~A ∴A ⊃ B ۲. ~A ∨ B ۳. A ⊃ B | ۱, Add. ۲, Impl. |
مثال ۲
۱. C
∴ D ⊃ C
این الگو نیز بسیار فراوان ظاهر میشود. درستی گزارهای مانند C دانسته است؛ که در اینجا بهعنوان یک مقدمه دادهشده؛ و نیز ممکن است درستی آن در برهانی طولانیتر درجایی از دنباله ثابتشده باشد. میدانیم گزارههای درست، بطور مادی مستلزَم بوسیله هر گزارهای، هرچه باشد، هستند. بنابراین هر گزاره را که انتخاب کنیم، در اینجا D، باید مستلزِم C باشد. میپرسیم: به گونه صوری چگونه میتوان D⊃C را از C استنتاج کرد؟
حل
D در مقدمه حاضر نیست اما در نتیجه حضور دارد، بنابراین باید بهگونهای D را درون گامهای دنباله وارد کرد. میتوان D را افزود، اما کار نخواهد کرد— چون بعد از جابجایی ترکیب فصلی و جایگزینی آن بوسیله کار زدن ..Impl با شرطی D⊃C~ روبرو میشویم که قطعاً آن نتیجهای نیست که بعد از همه اینها به دنبال آن بودیم. ما D⊃C را میخواهیم. برای به دست آوردن این نتیجه باید بجای D از اول D~ را میافزودیم. مشکلی نیست، آن را انجام میدهیم، چراکه افزایش مجوز افزودن فصلی هر گزاره، هرچه باشد، را به یک عبارت-گزارهای که میدانیم درست است میدهد. سپس کار زدن .Com و .Impl آنچه را که میخواهیم به ما خواهند داد. برهان صوری این استدلال (یا قطعه برهان، وقتیکه بخشی از یک برهان طولانیتر است) بهقرار زیر است:
| ۱. ۲. ۳. ۴. | C ∴ D ⊃ C C ∨ ~D ~D ∨ C D ⊃ C | ۱, Add. ۲, Com. ۳, Impl. |
توجه: بعد از تمرین متن ادامه دارد.
تمرین
(د) هر یک از تمرینهای به دنبالآمده الگوهای تکرارشونده معمول [در استدلالهای طولانیتر] را به نمایش میگذارند. ساختن برهان صوری آنها تااندازهای ابتکار میخواهد و (در بعضی حالات) برهان آنها نیازمند به هشت تا نه خط است. بااینحال، بیشتر این برهانها فقط کمی سخت هستند و تدوین استراتژیهای موردنیاز برای به دست آوردن آنها کاری ممتاز است. بنابراین، برای هریک از استدلالهای زیر یک برهان صوری تشکیل دهید.

بعد از تمرین بهاندازه و لازم وقتیکه فرد با ۱۹ قاعده استنتاج آشنا شد، آنوقت نوبت آن است تا پیگیر برهانهای صوری باشد که طولانیتر و تنیدهتر هستند. سه مجموعه تمرینی که به دنبال میآیند تااندازهای چالش به میان میآورند، اما تدبیر برهان صوری آنها منبعی برای اقناع گوهرین است. ریاضیدان بزرگ ج. اچ. هاردی / G. H. Hardy مدتها پیش ملاحظه کرده بود که تشنگی طبیعی و گستردهای برای "تکان لرزههای" فکری وجود دارد− و اینکه "هیچچیز دیگر بطور کامل این تکانلرزه را در خود ندارد" مگر آنچه در حل مسائل منطقی هست.
استدلال در زبان طبیعی، آنگونه که در دو مجموعه تمرین آخر آمده، نیازمند به توضیح بیشتر نیستند. بعد از برگرداندن آنها به نشانهگذاری نمادین با استفاده از کوتهسازیهای پیشنهادی، ساختن برهان برای آنها تفاوتی با وقتیکه یک برهان را با یک پیکربندی نمادین آغاز میکنیم ندارد. قبل از ماجراجویی بیشتر در اقلیم منطق، سودمند است تا دو مثال از مجموعه تمرین (ه) که ازاینپس با مانند آنها سروکار داریم را بررسی کنیم.
استدلالهایی که در همه این مجموعهها ارائهشدهاند معتبر هستند. و چون میدانیم دستگاه نوزده قاعدهای که گستراندهایم تمام است، بنابراین مطمئنیم که یک برهان برای هر یک از این استدلالها قابل ساختن است. با همه این احوال، مسیر از مقدمات تا نتیجه ممکن است نهچندان آشکار باشد. در هر حالت همانطور که فرد پیش میرود باید بعضی نقشه عمل را نیز تدبیر کرده باشد.
در اینجا ما نیازمندی به نقشه برای حمله و نیز راهی که چنین نقشههایی میتوانند تدوین شوند را، با بررسی بسیار نزدیک دو تمرین اول مجموعه (ه)، نشان میدهیم:
مثال ۱
۱. A ⊃ ~B
~( C • ~A)
∴C ⊃ ~B
حل
نتیجه این استدلال یک گزاره، C، را که در مقدمه دوم آمده با یک گزاره، B~، که در مقدمه اول آمده متحد (تک ساخت) کرده. چگونه میتوان این اتحاد (تک سازی) را به انجام رساند؟ اولین مقدمه یک شرطی است که تالی آن، B~، تالی نتیجه نیز است. دومین مقدمه شامل نقیض مقدم اولین مقدمه، A~ است. اگر بتوانیم با کار کردن روی مقدمه دوم، C⊃A را به دست دهیم، آنگاه میتوان تک سازی موردنظر را با کار زدن .H.S. به دست داد. میتوان آن را انجام داد. اگر .DeM را به مقدمه دوم بکار ببندیم یک ترکیب فصلی به دست میآوریم که با جایگزینی آن بوسیله .Impl فقط یک گام کوتاه از شرطی مطلوب فاصله خواهیم داشت. برهان صوری بهقرار زیر است:
| ۱. A ⊃ ~B ۲. ~( C • ~A) ∴C ⊃ ~B ۳. ~C ∨ ~~A ۴. C ⊃ ~~A ۵. C ⊃ A ۶. C ⊃ ~B | ۲, DeM. ۳, Impl. ۴, .D.N. ۵, ۱, H.S. |
توجه کنید در این برهان، مانند بسیاری دیگر، دنبالهای که به گونه دیگر تدوینشدهباشد نیز میتواند به همین سرانجام برسد. خط ۳ برای گام اول موردنیاز است. اما میتوانستیم ترکیب فصلی در خط ۴ را باقی بگذاریم و در آنجا فقط A را با A~~ جایگزین کنیم:
| ۴. ~C ∨ A | ۳, D.N. | نیاز است تا این خط با یک شرطی جایگزین شود. |
| ۵. C⊃A | ۴, Impl. | |
| ۶. C ⊃ ~B | ۵, ۱, H.S. | سرانجام، .H.S برهان را پایان میدهد. |
تفاوت بین این دو دنباله، در این حالت، عمدتاً در ترتیب است. گاهی برهانهای جایگزینی وجود دارند که بهکلی استراتژی متفاوتی را در پیشگرفتهاند.
بهعنوان آخرین توضیح جزئیات برهانهای صوری یکی از استدلالهای طولانیتر در مجموعه (ه)، تمرین ۲۰، را بررسی میکنیم، که تدبیر استراتژی در آن نیازمند به چالش بیشتری است.
مثال ۲
۱. (R ∨ S) ⊃ (T • U)
۲. ~R ⊃ (V ⊃ ~V)
۳. ~T ∴~V
نتیجهای که به دنبال آنیم، V~، فقط در دومین از این سه مقدمه ظاهرشده و تازه در آنجا مدفون در یک گزاره مرکب بزرگتر است. چگونه باید آن را ثابت کرد؟ درمییابیم که تالی دومین مقدمه (V⊃~V) یک شرطی است که اگر با یک ترکیب فصلی جایگزین شود، V∨~V~ را به دست میدهد، و این بهنوبت خود مستقلاً، بوسیله توتولوژی V~ را حاصل خواهد داد. میتوان (V⊃~V) را بوسیله M.P. به دست آورد؟ برای این کار نیاز به R~ است. R در مقدمه اول بهعنوان بخشی از یک ترکیب فصلی آمده؛ اگر بتوانیم نقیض این ترکیب فصلی را به دست آوریم، آنگاه خواهیم توانست R~ را به دست آوریم. برای به دست آوردن نقیض این ترکیب فصلی نیاز داریم تا نقیض تالی اولین مقدمه را به دست آوریم، چراکه بتوان .M.T را بکار زد. همینطور که میتوان دید نقیض تالی (T•U) باید در اختیار باشد. ازآنجاکه مقدمه سوم T~ را تصدیق میکند پس قطعاً اگر T~ درست باشد آنگاه قطعاً (T•U) نادرست است. چگونه باید این را نشان داد؟ به نقیض آنچه در پیاش هستیم نگاهی میاندازیم: (T•U)~. این منطقاً همارز با T∨~U~ است. بنابراین میتوان T∨~U~ را با افزودن U~ به T~ ثابت کرد. اکنون همه عناصر نقشه حاضرند؛ فقط باید آنها را درون یک دنباله نشتناپذیر گذاشت. این، وقتیکه استراتژی تدوینشده باشد، چیزی نیست که هرگز مشکل باشد. با ساختن نقیض تالی اولین مقدمه، کار را آغاز میکنیم، سپس نقیض مقدم آن مقدمه و بعداً R~ را به دست میآوریم. با R~ بوسیله M.P.، عبارت (V⊃~V) را به دست میدهیم، و اینجاست که نتیجهای که به دنبالش هستیم در دستان ما خواهد بود. خطهای واقعی این برهان صوری بهقرار زیر هستند:
| ۱. (R ∨ S) ⊃ (T • U) ۲. ~R ⊃ (V ⊃ ~V) ۳. ~T ∴~V | |
| ۴. ~T ∨ ~U | ۳, Add. |
| ۵. ~(T • U) | ۴, De M. |
| ۶. ~(R ∨ S) | ۱, ۵, M.T. |
| ۷. ~R • ~S | ۶, De M. |
| ۸. ~R | ۷, Simp. |
| ۹. V ⊃ ~V | ۲, ۸, M.P. |
| ۱۰. ~V ∨ ~V | ۹, Impl. |
| ۱۱. ~V | ۱۰, Taut, Q.E.D. |
بطور سنتی معمول است نتیجه یک برهان را با سه حرف .Q.E.D پایان داد— اظهار مباهاتی مختصر که از سرواژههای عبارت لاتینی— Quod erat demonstrandum — "این همان است که میخواستیم" به دست میآید.
تمرین

تمرین
(و) برای هریک از استدلالهای زیر یک برهان صوری بسازید و در هریک نشانههای پیشنهادی را به کاربرید.
۱*. مدیریت متوجه دگرگونی نشده یا آن را تصویب کرده. وی به همه موارد توجه کرده. بنابراین او باید آن را تصویب کرده باشد. (N، A)
۲. اکسیژن در لامپ با فیلایمان ترکیب میشود و تشکیل اکسید میدهد یا بطور کامل ناپدید خواهد شد. اکسیژن نمیتواند بطور کامل ناپدید شود. بنابراین اکسیژن در لامپ با فیلایمان ترکیب میشود و تشکیل اکسید میدهد. (C، V).
۳. اگر یک رهبر سیاسی پی برد که عقاید پیشینش نادرست است و سعی در تغییر آنها نکند، وی به خاطر فریبکاری مقصراست؛ اما اگر تغییر رفتار دهد به خاطر ناسازگاری در رفتار مسئول است. وی رفتارش را تغییر خواهد داد یا نخواهد داد. بنابراین به خاطر فریبکاری مقصر خواهد بود یا مسئول ناسازگاری در رفتار خود است(A, D, I).
۴. اینگونه نیست که او آن را فراموش کرده باشد یا نمیتوانسته آن را انجام دهد. بنابراین او میتوانسته آن را انجام دهد(F، A).
۵*. اگر کاغذ تورنسل قرمز شود آنگاه محلول اسیدی است. بنابراین اگر کاغذ تورنسل قرمز شود آنگاه محلول اسید است یا جایی اشتباهی رخداده (R، A، W).
۶. او میتواند دارای دوستان زیادی باشد اگر فقط آنها را بطور فردی مورداحترام قرار دهد. اگر آنها را بطور فردی مورداحترام قرار دهد نمیتواند از آنها انتظار داشته باشد که همه شبیه هم رفتار کنند. او دوستان زیادی دارد. بنابراین او انتظار ندارد همه آنها مثل هم رفتار کنند. (F، R، E).
۷. اگر در جیب قربانی پول وجود دارد آنگاه انگیزه جنایت نمیتواند دزدی باشد. اما انگیزه جنایت دزدی یا انتقام است. در جیب قربانی پول وجود دارد. بنابراین باید انگیزه جنایت انتقام باشد(M، R، V).
۸. اگر ناپلئون غاصب قدرتی بود که بطور قانونی از آن او نبود باید محکوم شود. ناپلئون یک سلطان قانونی بود یا غیرقانونی قدرت را غصب کرده بود. ناپلئون یک سلطان قانونی نبود. بنابراین ناپلئون باید محکوم شود. (C، U، L).
۹. اگر اعتبار حساب ویژه پژوهش را گسترش دهیم وظیفه اخلاقی آنهاست تا در پروژه بعدی پیشنهاد ما را بپذیرند. ما میتوانیم حاشیه سود مناسبتری را در برآورد خود ملحوظ کنیم اگر آنها مطابق وظایف اخلاقی در پروژه بعدی پیشنهاد ما را بپذیرند. ملحوظ کردن حاشیه سود مناسبتر در برآورد موجب میشود وضع عمومی مالی ما بطور قابلملاحظه بهبود یابد. بنابراین بهبودی قابلملاحظه وضع عمومی مالی ما ناشی از گسترش بیشتر حساب ویژه پژوهش خواهد بود. (C, M, P, I).
۱۰*. اگر قوانین خوب و اجرای آنها استوار باشد آنگاه جنایت کاهش میابد. اگر اجرای استوار قوانین جنایت را کاهش میدهد پس مسئله ما در عمل است. قوانین خوب هستند. بنابراین مسئله ما در عمل است. (G, S, D, P ).
۱۱. اگر تمدن رومی پابند به آزادی شهروندان بود آنگاه شهروندان رومی بهرهمند از آزادی مذهب بودند. اگر شهروندان رومی بهرهمند از آزادی مذهب بودند آنگاه اعدامهای مسیحیان نخستین وجود نداشت. اما مسیحیان نخستین اعدام میشدند. بنابراین شهروندان رومی نمیتوانستند از آزادیهای شهروندی بهرهمند باشند. ( G, F, P).
۱۲. اگر اولین فصل ترکیب فصلی درست باشد آنگاه ترکیب فصلی درکل درست است. بنابراین اگر فصل اول و دوم ترکیب فصلی درست باشند آنگاه ترکیب فصلی درکل درست است.(F, W, S).
۱۳. اگر محل دادگستری جدید باید جای مناسبی باشد باید در مرکز شهر باشد؛ و اگر از جهت کارکردها باید قابلقبول باشد باید بهاندازه کافی وسیع باشد تا همه دفاتر لازم را در خود جای دهد. اگر دادگستری جدید در مرکز شهر قرار گیرد و به حد کافی وسیع باشد تا همه دفاتر لازم را در خود جای دهد، آنگاه هزینه آن بیشتر از 10 میلیون دلار خواهد شد. هزینه نباید بیشتر از 10 میلیون دلار شود. بنابراین دادگستری جدید در محل مناسبی نخواهد بود یا از جهت کارکردهایش قابلقبول نخواهد بود. (C، H، E، L، O).
۱۴. اگر جمال پیام را دریافت کند میآید ولی بهشرط آنکه هنوز علاقهمند باشد. گرچه او نیامد ولی هنوز علاقهمند است. بنابراین او پیام را دریافت نکرده. (C، M، A ).
۱۵* . چنانچه برآورد موزاییکی پیدایش گیتی (برآورد خلقت در کتاب تورات/سفر پیدایش) بهواقع درست باشد، آنگاه خورشید تا روز چهارم خلق نشده بود. اگر خورشید تا روز چهارم خلق نشده باشد، آنگاه نمیتوانسته در سه روز اول باعث گردش شب و روز شده باشد. کلمه "روز" در متون مقدس معنای دیگری جز آنچه هماکنون بطورمعمول پذیرفتهشده دارد یا خورشید باید علت گردش شب و روز برای سه روز اول بوده. بنابراین میتوان نتیجه گرفت پیدایش موزاییکی گیتی بهواقع درست نیست یا کلمه روز به معنای متفاوت دیگری ازآنچه اکنون از آن فهمیده میشود بکار رفته. (M، C، A، D).
۱۶. اگر صندوقدار دکمه اخطار را فشار داده بود صندوق بطور خودکار قفل میشد و پلیس در عرض سه دقیقه میرسید. اگر پلیس در عرض سه دقیقه رسیده بود به ماشین رباینده میرسید و آن را میگرفت. اما ماشین رباینده گرفته نشده. بنابراین صندوقدار دکمه اخطار را فشار نداده. (T، C، V،P، O ).
۱۷. اگر آدمیان همیشه مطابق احساس وظیفه عمل کنند آنگاه آنها باید از بسیاری لذات چشمپوشی نمایند؛ و اگر مطابق تمایلاتشان برای لذات رفتار نمایند آنگاه بیشتر وقتها از وظایف خود غفلت میکنند. انسانها یا همیشه مطابق احساس وظیفه رفتار میکنند یا مطابق تمایلاتشان برای لذات رفتار میکنند. اگر آدمیان همیشه مطابق احساس وظیفه عمل کنند آنگاه بیشتر وقتها از وظایف خود غفلت نخواهند کرد؛ و اگر مطابق تمایلاتشان برای لذات رفتار نمایند آنگاه از بسیاری لذات چشمپوشی نخواهند کرد. بنابراین آدمیان از بسیاری لذات چشمپوشی خواهند کرد اگر و تنها اگر بیشتر اوقات از وظایف خود غفلت نکنند(D, F, P, N).
۱۸. گرچه جمعیت دنیا رو به افزایش است، محصولات کشاورزی رو به کاهش و تولیدات صنعتی ثابت مانده. اگر محصولات کشاورزی رو به کاهش و جمعیت جهان روبه افزایش باشد، یا منابع جدید غذایی پیدا خواهند شد یا باز توزیع ریشهای منابع غذایی در جهان رخ خواهد داد مگر آنکه نیاز غذایی بشر کاهش یابد. هیچ منبع غذایی جدید پیدا نخواهد شد و بعلاوه نه برنامههای تنظیم خانواده پیش خواهد رفت و نه نیاز غذایی بشر کاهش خواهد یافت. بنابراین باز توزیع ریشهای منابع غذایی در جهان رخ خواهد داد(V, A, M, N, R,H).
۱۹. دزد از در واردشده یا جنایت اندرونی است و پای یکی از خدمتگزاران در میان است. دزد نمیتوانسته از بیرون آمده باشد مگر آنکه چفت در از داخل بازشده باشد؛ اما پای یکی از خدمتگزاران در میان خواهد آمد اگر چفت در از داخل بازشده باشد. بنابراین پای یکی از خدمتگزاران در میان است .( D، I، S، L).
۲۰*. اگر شهریه را پرداخت کنم پولی برایم نخواهد ماند. فقط اگر پول داشته باشم یک کامپیوتر خواهم خرید. نمیتوانم برنامهسازی کامپیوتر را یاد بگیرم مگر آنکه یک کامپیوتر بخرم. اما اگر شهریه را پرداخت نکنم نمیتوان در کلاس ثبتنام کنم؛ و اگر در کلاس ثبتنام نکنم قطعاً کامپیوتر نخواهم خرید. درهرصورت باید شهریه را بپردازم یا نپردازم. بنابراین قطعاً برنامهسازی کامپیوتر را یاد نخواهم گرفت. (P، M، C، L، E)
تمرین
(ز) پنج استدلال زیر معتبر هستند و برهان اعتبار هریک از آنها موردنظر است. ساختن برهان آنها بهگونهای از آنان که در تمرین قبلی بودند سختتر است. دانشجویانی که گاهی خود را درمانده یابند نباید دچار ناامیدی شوند. آنچه میتواند در برآورد اول سخت به نظر آید در ادامه پایستگی میتواند بسیار کمتر سخت به نظر آید. دانستن 19 قاعده استنتاج و تکرار در کار زدن این قاعدهها کلید ساختن این براهین هستند.
۱. اگر علوم انسانی بخوانی، فهم از آدمیان را گسترش خواهی داد و اگر علوم تجربی بخوانی فهم از جهان دوروبرت را گسترش خواهی داد. بنابراین اگر علوم انسانی بخوانی یا علوم تجربی بخوانی، فهم از آدمیان یا از جهان دوروبرت را گسترش خواهی داد(H, P, S, W).
۲. اگر علوم انسانی بخوانی، فهم از آدمیان را گسترش خواهی داد و اگر علوم تجربی بخوانی فهم از جهان دوروبرت را گسترش خواهی داد. بنابراین اگر هم علوم انسانی بخوانی وهم علوم تجربی بخوانی، فهم از آدمیان و فهم از جهان دوروبرت را گسترش خواهی داد(H, P, S, W).
۳. اگر تو توان انتخاب آزادانه داشته باشی آنگاه هیچیک از اعمال تو توسط رویدادهای پیشین قطعیت نمییابند. اگر تو توان انتخاب آزادانه داشته باشی آنگاه اگر اعمال تو توسط هر رویداد پیشینی قطعیت یافته باشند، اعمال تو نمیتوانند قابل پیشبینی باشند. اگر اعمال تو توسط هر رویداد پیشینی قطعیت نیافته باشند آنگاه اگر اعمال تو قابل پیشبینی نباشند آنوقت نتیجه اعمال تو نیز پیشبینی پذیر نیستند. بنابراین اگر تو توان انتخاب آزادانه داشته باشی نتیجه اعمال تو پیشبینی پذیر نخواهند بود (F، A، P، C).
۴. سقراط یک فیلسوف بزرگ بود. بنابراین سقراط ازدواج باخوشی داشت یا نداشت (G، H).
*5. اگر سقراط ازدواج باخوشی داشت یا نداشت، سقراط فیلسوف بزرگی بود. بنابراین سقراط فیلسوف بزرگی بود (H، G).