تکنیک کوتاهترِ جدول ارزش (STTT)
روشهای استنتاج
درآمد به منطق فصل ۱۰ قسمت ۹
در فصل ۹ در قسمت ۶ ( آزمون اعتبار استدلال بر پایه جدول ارزش) را دیدیم و نیز ناکارآمدی آن که برخاسته از رشد تصاعدی تعداد سطرهای جدول ارزش بر حسب افزایش تعداد گزارههای ساده متمایز (یا متغیرهای گزارهای) در استدلال (یا صورت استدلال) بود. در این قسمت یک روش کارآمد برای ساخت کوتاهترِین جدول ارزش (STTT - Shorter Truth-Table Technique) در آزمون اعتبار و بیاعتباری استدلال را ارایه و آن را توضیح میدهیم.
۹.۱۰ تکنیک کوتاهترِ جدول ارزش (STTT)
تکنیک کوتاهترین جدول-ارزش
The Shortest possible Truth Table Technique
STTT برای تعیین اینکه آیا یک استدلال (یا صورت استدلال) معتبر است یا نه به کار میرود؛ اینگونه که آیا ممکن است برای ترکیبی از مقادیر ارزش برای گزارههای ساده (یا متغیرهای گزارهای) همهی مقدمات آن درست باشند و نتیجه آن نادرست باشد؛ که در آن یا (الف) نتیجه نادرست است و یا (ب) مقدمات همه درست هستند. ۶
روشن است که برای یک استدلال نامعتبر، هیچ برهان صوری اعتبار وجود ندارد. با این وجود، اگر نتوانیم یک برهان صوری اعتبار برای آن پیدا کنیم، این نتوانستن ثابت نمیکند که استدلال بیاعتبار است و نمیتوان چنین برهانی را ساخت. ممکن است فقط این باشد که ما به اندازه کافی تلاش نکردهایم. ناتوانی ما در یافتن برهان اعتبار ممکن است ناشی از این باشد که استدلال معتبر نیست، اما میتواند ناشی از نبود توان ابتکار در ما — به علت ویژگی غیر کارآمد بودن روند ساخت برهان باشد. ناتوانی در ساختن برهان صوری برای اعتبار یک استدلال، بیاعتباری آن را ثابت نمیکند. چه چیزی میتواند ثابت کند که یک استدلال دادهشدهای بیاعتبار است؟
یک جدول ارزش میتواند تشکیل دهنده برهانی برای بیاعتباری یک استدلال باشد. روش جدول ارزش کامل (Complete Truth-Table Method / CTTM)، که در قسمت ۹.۶ به تفصیل شرح آن آمده، یک روند تصمیمگیری برای تعیین اعتبار یا عدم اعتبار در منطق گزارهای است. این یک روش مستحکم است که هرگز ناکام نمیشود. اما روشی دست و پا گیر و ناکارآمد است. ما در اینجا دنبال تکنیکی هستیم که بتواند همان نتایج کاملاً قابل اطمینان را بطور کارآمدتر ارائه دهد. این روش را تکنیک کوتاهترین جدول-ارزش ممکن (the shortest possible truth table و از این پس STTT) مینامیم.
به یاد داشته باشید که در یک استدلال استنتاجی معتبر ممکن نیست همه مقدمات درست و نتیجه نادرست باشد. در آزمون یک استدلال یا صورت استدلال با استفاده از CTTM، ما یک جدول ارزش کامل ایجاد میکنیم و سپس همه مواردی که در آن نتیجه نادرست است را بررسی میکنیم تا مشخص شود، آیا در هر یک از این حالتها همه مقدمات درست هستند یا خیر. اگر چنین موردی وجود داشت، استدلال نامعتبر است؛ وگرنه استدلال معتبر است.
انگیزه برای STTT از این جهت است که در جدول ارزش نیاز است تا فقط همه آن حالاتی بررسی شوند که در آن نتیجه نادرست است (یا همه حالاتی که در آنها همه مقدمات درست است)، بنابراین ساختن یک جدول ارزش کوتاهتر صرفاً برای آن سطرها که نتیجه در آن سطرها نادرست است (یا فقط همه آن سطرها که همه مقدمات درست است) بسیار کارآمدتر است.
برای مثال، صورت استدلالی
(P۱): p ⊃ (q • r)
(P۲): (q ⋁ r) ⊃ s
∴ p ⊃ s
دارای چهار متغیرهای گزارهای و ۲۴ یا ۱۶ سطر است. اما میتوان با استفاده از STTT و ساختن جدول ارزش کوتاهتر یک سطری زیر معین کرد که استدلال معتبر است.➥

نتیجه، p⊃s، فقط وقتی نادرست است که p درست و s نادرست باشد. ازآنجاکه، p مقدم p⊃(r•r) است، مقدمه ۱ فقط وقتی درست است که تالی آن، q•r، درست باشد. اما q•r تنها وقتی درست است که q درست و r درست باشد، بهعبارت دیگر وقتی q درست، r درست و s نادرست است، مقدمه ۲ نمیتواند درست باشد. این بجای ۱۶ سطر تنها در یک سطر ثابت میکند که استدلال معتبر است زیرا نشان میدهد بر مبنای تنها مقادیر ارزش p و s که نتیجه را نادرست میسازند دو مقدمه هر دو نمیتوانند درست باشند.
ما از STTT برای ساختن کوتاهترین جدول ارزش ممکن استفاده میکنیم تا مشخص کنیم که آیا ممکن است یک استدلال (یا صورت استدلال) دارای همه مقدمات درست و یک نتیجه نادرست باشد. در اجرای STTT ثابت میکنیم که این میتواند ممکن باشد (پس استدلال نامعتبر است) یا نمیتواند ممکن باشد (پس استدلال معتبر است).
بیاعتبار:
جدول ارزش کوتاهتر با اثبات اینکه ممکن است استدلال (یا صورت استدلال) دارای همه مقدمات درست و نتیجه نادرست باشد، ثابت میکند که استدلال (یا صورت استدلال) نامعتبر است. جدول ارزش کوتاهتر این امکان را با ساخت یک سطر از جدول ارزش ثابت میکند، سطری که در آن نتیجه نادرست است و همه مقدمات برای یک ترکیب از مقادیر ارزش برای گزارههای ساده (یا متغیرهای گزارهای) درست هستند.

اعتبار:
جدول ارزش کوتاهتر با اثبات اینکه ممکن نیست استدلال (یا صورت استدلال) دارای همه مقدمات درست و نتیجه نادرست باشد، ثابت میکند که استدلال (یا صورت استدلال) معتبر است. جدول ارزش کوتاهتر این عدم امکان را با نشان دادن اینکه همه مقدمات برای هر سطر با نتیجه نادرست درست نیستند (یا اینکه نتیجه برای هر سطر که در آن همه مقدمات درست هستند نادرست نیست) اثبات میکند. برای مثال، برای یک استدلال معتبر با یک گزاره ساده بعنوان نتیجه، جدول ارزش کوتاهتر به ضرورت دارای حداقل یک مقدمه نادرست است.

در ادامه این قسمت، ما بجای صورتهای استدلالی، استدلالها را برای اعتبار خواهیم آزمود. بنابراین در آنچه میآید، مقادیر ارزش را به گزارههای ساده یک استدلال گمارده تا مشخص کنیم آیا آن استدلال معتبر است یا نه.
آ مهارت ضروری: گمارش اجباری و غیراجباری مقادیر ارزش
برای کارزدن STTT ابتدا باید چگونگی گمارش مقادیر ارزش به گزارههای ساده و گزارههای مرکب را آموخته و افزون بر آن چگونگی گمارش اجباری مقادیر ارزش را بیاموزیم. فرض کنید میخواهیم بدانیم آیا استدلال زیر معتبر است یا نه.
(P۱): D ⊃ G
(P۲):: G ⊃ H
∴ D ⊃ H
برای کار زدن STTT ابتدا نتیجه را نادرست میسازیم. نتیجه این استدلال گزاره شرطی زیر است:
D ⊃ H
برای اینکه نشان دهیم این گزاره شرطی نادرست است در زیرِ عملگر منطقی اصلی آن یک F قرار داده:
D ⊃ H
F
اگر این گزاره شرطی که شامل گزارههای ساده H و D است نادرست باشد آنگاه باید D درست و باید H نادرست باشد. هنگامی که روند STTT را اجرا میکنیم، مقادیر ارزش را به گزارههای مرکب، همانطور که هستند، گمارده، و اغلب مقدار ارزش یک گزاره مرکب، مانند نادرستی D•H، ما را اجبار میکند تا به گزارههای ساده و در این مورد به D و H مقدار ارزش خاصی را گمارده. بنابراین، در این حالت ما مجبور هستیم تا مقدار درست (T) را به D و مقدار نادرست (F) را به H اختصاص دهیم.
D ⊃ H
T F F
گمارشهای مقدار ارزش به D و H گمارشهای مقدار ارزش اجباری هستند. آنها باتوجه به نادرستی D⊃H مجبوراند چنین باشند. با توجه به جدول ارزش تعریفشدهیِ شرطی ارائه شده در فصل ۹ چنیناند. یک گزاره شرطی تنها در صورتی نادرست است که مقدم آن درست و تالی آن نادرست باشد. بنابراین، اگر D⊃H نادرست باشد آنگاه بایی D درست و باید H نادرست باشد. ما یک گمارش اجباری مقدار ارزش را بعنوان گمارش یک مقدار ارزش به یک گزاره ساده یا مرکب اینگونه تعریف میکنیم که ناگزیر در دایره سه گانه زیر باشد:
سرشت تابع–ارزشی گزارههای ساده و مرکب،
هدف(های) ما و/یا
گمارشهای مقادیرِ ارزش از پیش گماردهشده.
در اجرای STTT، همانطور که باید نتیجه را نادرست سازیم، باید با گمارش مقادیر ارزش به گزارههای ساده تشکیل دهنده آنها، مقدمات را درست سازیم. برای مثال فرض کنید که یک استدلال دارای عطفی E•F به عنوان مقدمه است و میخواهیم آن را درست سازیم.
D • H
T
گمارش مقدار ارزش به E و F اجباری است زیرا، میدانیم که این رابط تنها در صورتی درست است که E درست و F درست باشد.
D • H
T T T
برای مثال سوم، فرض کنید که نتیجه یک استدلال، فصلی G∨J است که میخواهیم آن را نادرست سازیم.
G ∨ J
F
همانطور که از فصل ۹ میدانیم، یک فصلی تنها در صورتی نادرست است که هر دو فصل آن نادرست باشند. بنابراین، گمارشهایی که باید برای G و J انجام دهیم، گمارشهای مقدار ارزش اجباری هستند: G باید نادرست باشد و J باید نادرست باشد.
G ∨ J
F F F
در روند اجرای STTT، هر وقت به یک نتیجه یا یک مقدمه در یک گزاره ساده یک مقدار ارزش گمارده شود، باید به طور سازگار همان مقدار ارزش را به آن گزاره ساده در هر جا که در استدلال رخ میدهد، بگماریم. برای مثال، فرض کنید که STTT را برای استدلالی اجرا میکنیم که گزاره ساده M را به عنوان نتیجه دارد و یکی از مقدمات استدلال R⊃M است. هنگامی که در نتیجه مقدار نادرست (F) را به M گماردیم، باید پیوسه همان مقدار ارزش را به M در مقدمه R⊃M گمارش کنیم.
R ⊃ M
F
در این مقطع میکوشیم تا این مقدمه را دارای مقدار ارزش درست کنیم. همانطور که میدانیم یک شرطی با تالی نادرست تنها در صورتی درست است که مقدم آن نادرست باشد. بنابراین، برای دارای مقدار ارزش درست شدن این شرطی، با توجه به نادرستی تالی آن، M، مجبوریم مقدار ارزش نادرست (F) را به R بگماریم.
R ⊃ M
F T F
گمارش مقدار ارزش نادرست به R یک گمارش اجباری مقدار ارزش است: این اجبار توسط سه عامل است:
(۱). M هماکنون دارای مقدار ارزش نادرست است،
(۲). هدف ما این است که این مقدمه شرطی را دارای مقدار ارزش درست سازیم و
(۳). یک شرطی با تالی نادرست تنها در صورتی درست است که مقدم آن نادرست باشد.
فرض کنید، نتیجه یک استدلال، عطفی K•N باشد، و میخواهیم مقدار ارزش آن را نادرست سازیم.
K • N
F
در این مثال، آیا مجبوریم تا به گزارههای ساده K و N گمارش مقدار ارزش خاصی گمارده؟ خیر چنین نیست. هیچ گمارش اجباری مقدار ارزشی در کار نیست زیرا عطف گزارههای ساده از سه راه نادرست است:
T • F، F • T و F • F.➥
در این مورد، گمارشهای غیراجباری مقدار ارزش را انجام میدهیم و برای هر ترکیب مقدار ارزش که در آن ترکیب عطفی نادرست است، یک سطر جداگانه میسازیم.
K • N
TF F
FF T
FF F
برای انجام گمارش صحیح مقدار ارزش - اجباری و غیراجباری - ضروری است که جداول ارزش تعریفی برای پنج عملگر منطقی را که در فصل ۹ ارائه شد، بدانیم. توصیه میکنیم تا جداول ارزش تعریف و قوانین سرانگشتی را برای عملگرهای منطقی مرور کنید (فصل ۹ قسمت ۶ — ما برای دسترسی آسان آنها را اینجا آوردهایم.)
- ترکیب عطفی: یک ترکیب عطفی فقط وقتی درست است که هر دو عطف آن درست باشد. در غیر این صورت نادرست است.
- ترکیب فصلی: یک ترکیب فصلی فقط وقتی نادرست است که هر دو فصل آن نادرست باشد. در غیر این صورت درست است.
- ترکیب شرطی: یک ترکیب شرطی فقط وقتی نادرست است که مقدمه آن درست و تالی آن نادرست باشد. در غیر این صورت درست است.
- دو شرطی: یک دو شرطی فقط وقتی درست است که عبارتهای-گزارهای دو طرف رابطِ آن درست باشد.
- نقیض: نقیض وقتی درست است که عبارت-گزارهای نقض شده نادرست باشد. در غیر این صورت نقیض نادرست است. (یک نقیض دارای ارزش مخالف گزاره نقض شده است).
همانطور که قواعد سردستی نشان میدهند، مقادیر ارزش گزارههای مرکب، گمارش مقدار ارزش را مطابق با جداول ارزش تعریفی به راههای زیر ومیدارد.
| ترکیب عطفی | G•H درست است: | G را درست و H را درست سازید. |
| ترکیب فصلی | G∨H درست است: | G را نادرست و H را نادرست سازید. |
| ترکیب شرطی | G⊃H درست است: | G را درست و H را نادرست سازید. |
| نقیض | ~G درست است: ~G درست است: | G را نادرست سازید. G را درست سازید. |
در گمارش اجباری مقادیر ارزش است که STTT کارآمدی بالای خود را نشان میدهد. برای اطمینان از اینکه گمارش مقادیر ارزش اجباری به طور کارآمد و منظم انجام شوند، میباید در انطباق با دو راهبری (MAXIM) زیر انجام شوند.
| راهبری I | در صورت امکان، ابتدا گمارش مقادیر ارزش اجباری را به نتیجه یا مقدمه، همانطور که در گامهای ۱ از ۴ گام STTT تعیین شده است، انجام دهید (به بخش (ب)، در زیر مراجعه کنید). |
| راهبری II | گمارش مقادیر ارزش اجباری به مقدماتی که گزارههای ساده یا نقیض گزارههای ساده هستند را پیش از گمارش مقادیر ارزش اجباری به مقدمات ترکیبیتر انجام دهید. |
برای اطمینان از اینکه گمارش مقادیر ارزش غیراجباری بهطور کارآمد و سیستماتیک انجام میشوند، مطابق با راهنماهای III، IV و V انجام میشوند.
| راهبری III | اگر گمارش مقادیر ارزش اجباری یا بیشتر وجود ندارد - یا بیشتر وجود ندارد، گمارش مقادیر ارزش غیراجباری را تا پایان به نتیجه به انجام برسانید تا از هر راه ممکن نادرست شود، یا گمارش مقادیر ارزش غیراجباری را به مقدماتی انجام دهید که در کمترین تعداد راه درست است. |
| راهبری IV | اگر گمارش مقادیر ارزش به دو یا چند مقدمه به طور معادل اجباری است (مثلاً به دو گزاره ساده) یا به همان اندازه غیراجباری است، ابتدا گمارش مقادیر ارزش در سمت چپترین را انجام دهید. |
| راهبری V | در ساخت یک جدول ارزش کوتاه چند سطری، یک نتیجه نادرست (یا یک مقدمه درست) بسازید (الف) فقط با استفاده از آن دسته از ترکیبات مقادیر ارزش که مقدار ارزش دلخواه را برای آن گزاره مرکب بهدست میدهند، و (ب) آنها را به ترتیبی مرتب کنید که در یک جدول ارزش تمامشده پدیدار میشوند (به بخش ۹.۶ - آزمون اعتبار با جدول ارزش - مراجعه کنید). برای مثال، برای یک گزاره مرکب متشکل از دو گزاره ساده، به ترتیب، فقط از آن ترکیبهای TT، TF، و FT و FF استفاده کنید که مقدار ارزش مورد نظر را برای برای عبارت-گزارهای بهدست میدهند. |
گمارش مقادیر ارزش اجباری و استفاده از راهبری I تا V را (با عنوان STTT) که در بند (ب) این قسمت ارائه شده است. خواننده بهویژه و با توجه به توضیح و کارزدن آنها برای هفت استدلال متمایز که در بندهای (ج) و (د) نشان داده شده است به درک بهتر از این روش دست خواهد یافت. قدرت و کارایی بسیار بالای STTT زمانی که به STTT مسلط شوید کاملاً جاافتاده خواهد شد. مانند همیشه، تمرین راهگشا به چیرگی میشود. ما خواننده را تشویق میکنیم تا با تکمیل تمرینهای تعیین مقدار-ارزش در زیر، و سپس ۲۴ تمرین STTT در پایان بند (د) به این روش چیرگی یابد.
تمرین
گمارش مقادیر ارزش غیراجباری و اجباری
برای عبارتهای-گزارهای زیر، اگر گمارش مقادیر ارزش اجباری وجود دارد، آنها را انجام دهید. اگر هیچ گمارش مقادیر ارزش اجباری وجود ندارد، با استفاده از راهبری V، ترکیبهای مقادیر ارزش مورد نیاز را تعیین کنید که بر اساس آن، و تعداد راههایی که عبارت-گزارهای، بر حسب مورد، میتواند درست (یا نادرست) باشد، .
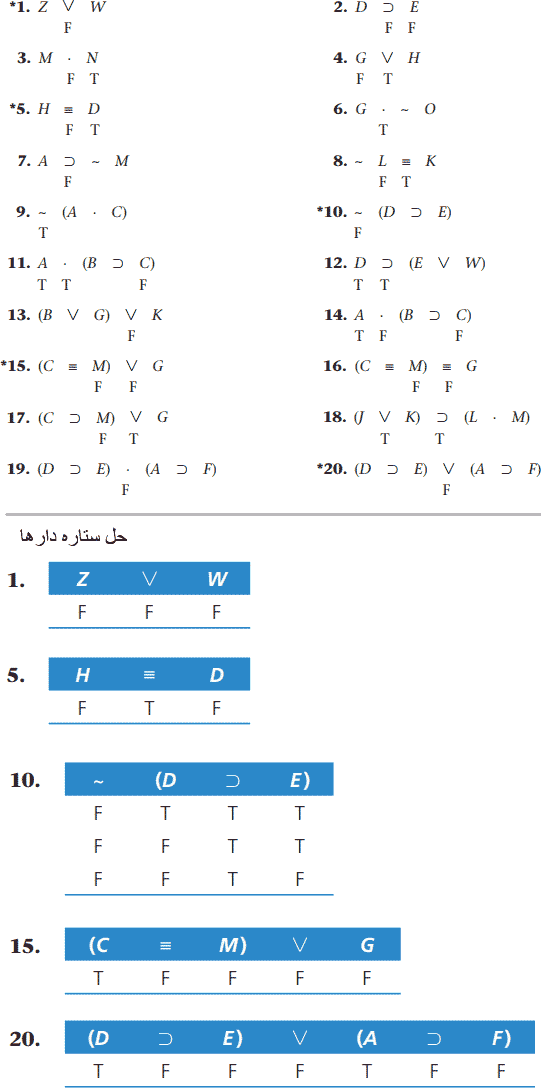
ب. چهار گام تکنیک جدول ارزش کوتاهتر
STTT یک روند چهار گامی است. این گامهای به صورت یکی از دو دنباله اعمال متمایز انجام میشوند. هر یک از این دو دنباله اعمال بطور صحیح تعیین میکنند که آیا یک استدلال داده شده معتبر است یا نه. تعیین اینکه کدام یک از دو مسیر باید دنبال شود — به عبارت دیگر، کدام یک از دو مسیر برای یک استدلال معین کارآمدتر است — در هر دو دنباله، در اولین گام یکی است، و بنابراین در هر دو یکسان است.
بیشتر گزارههای مرکب به بیش از یک راه، یعنی برای بیش از یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده خود، درست یا نادرست میشوند.➥۹
از این به بعد، وقتی از تعداد راههایی صحبت میکنیم که از آن راه یک گزاره مرکب میتواند درست (یا نادرست) باشد، منظور ما تعداد ترکیبی از مقادیر ارزش برای گزارههای ساده تشکیلدهنده آن است که آن گزاره مرکب را درست (یا نادرست) میکند. برای مثال، Q∨R به سه راه درست است: Q درست و R درست؛ Q درست است و R نادرست؛ و Q نادرست و R درست. به طور مشابه، M•N به سه راه نادرست است: M درست و N نادرست باشد؛ M نادرست و N درست باشد؛ و M نادرست و N نادرست باشد. با این حال، برخی از گزارههای مرکب تنها به یک راه درست یا نادرست هستند: برای مثال، Q⊃R فقط در صورتی نادرست است که Q درست و R نادرست باشد. و W•X فقط در صورتی درست است که W درست و X درست باشد.
چهار گام تکنیک جدول ارزش کوتاهتر
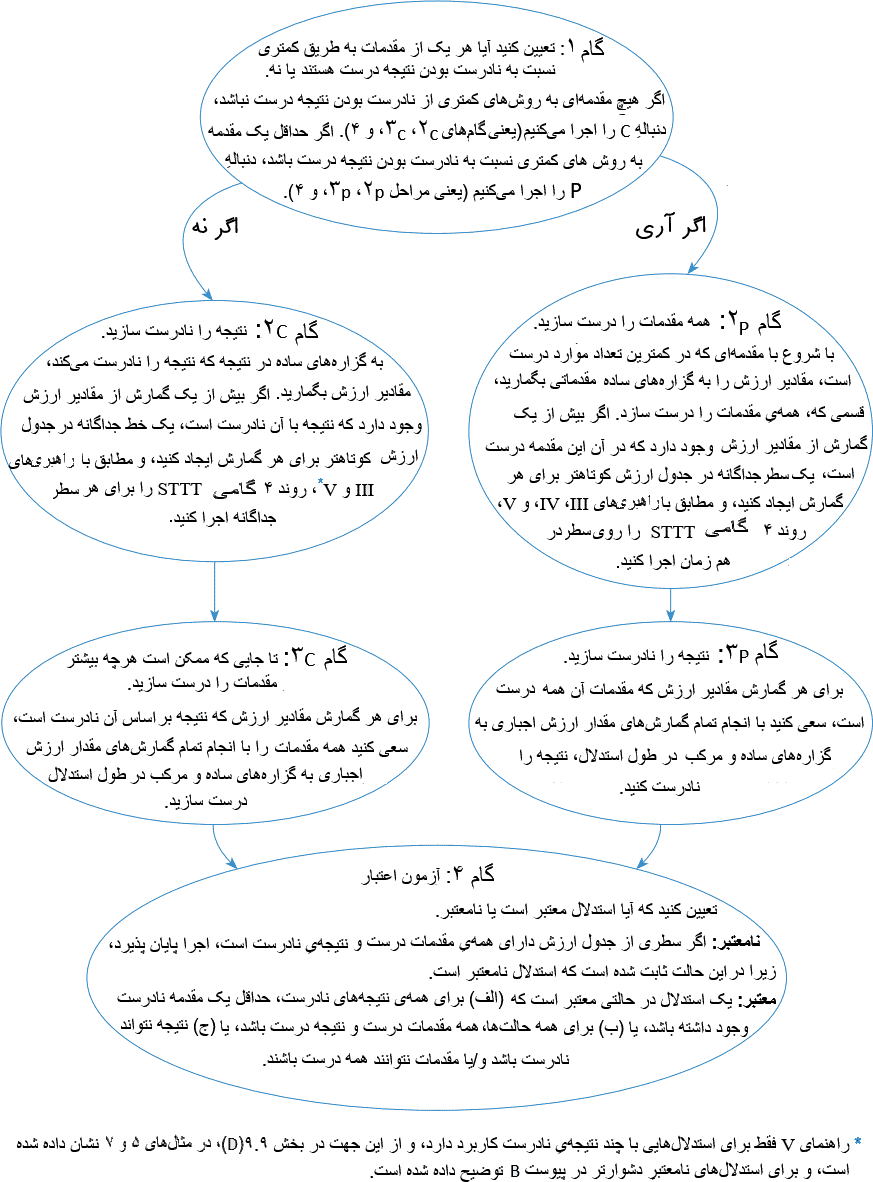
در دو بند بعدی، ما STTT را برای استدلالهایی که نتیجههای آنها فقط به یک راه نادرست است (بند ج) و برای استدلالهایی که نتیجههای آنها به روشهای متعدد نادرست است (بند د) اعمال میکنیم. خواهیم دید که گامهای ۳C، ۲C ، و ۴ کارآمدترین روش را برای استدلالهای قبلی ارائه میدهند، و زمانی که استدلالها نتایجی دارند که از چند راه نادرست هستند، انتخاب صحیح یکی از دو دنباله در گام ۱ باعث صرفه جویی در زمان و کار میشود.
ج. دنبالهِ-C در حالت ساده: نمونه برای استدلالی که نتیجه آن فقط از یک راه نادرست است
STTT زمانی بیشترین کارایی را دارد که نتیجه استدلال تنها برای یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن نادرست باشد. در این بند، گامهای ۳C، ۲C ، و ۴ را برای چهار استدلال از این گونه نشان میدهیم، و در هر مورد STTT را در یک جدول یک سطری اجرا میکنیم.
مثال ۱: یک استدلال ساده که در آن نتیجه یک گزاره ساده است.
مثال ۲: یک استدلال مرکب که در آن نتیجه یک گزاره ساده است.
مثال ۳: یک استدلال که در آن نتیجه سرطی است.
مثال ۴: یک استدلال که در آن نتیجه یک فصلی است.
مثال ۱: یک استدلال ساده که در آن نتیجه یک گزاره ساده است
استدلال ساده زیر را در نظر بگیرید.
(P۱): F ⊃G
(P۲): F
∴ G
برای ساختن یک جدول ارزش کوتاهتر، مقدمات را به ترتیب مینویسیم، هر کدام را با کاما (,) از بعدی آن جدا میکنیم، و مقدمه آخر را از نتیجه با سه نقطه برای «بنابراین» (∴) متمایز میکنیم. در سمت چپ مقدمه اول، برای هر گزاره ساده یک "ستون" راهنما ایجاد میکنیم.

گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه گزارهیِ ساده G است که تنها از یک راه نادرست است، و آن وقتی است که G نادرست باشد. از آنجا که هیچ مقدمهای نمیتواند به راههای کمتری درست باشد، گامهای ۳C، ۲C ، و ۴ را ادامه میدهیم.
گام ۲C: نتیجه را نادرست سازید.
تنها یک راه برای نادرست بودن نتیجه این استدلال وجود دارد: گزاره ساده G باید نادرست باشد. بنابراین، یک F (نادرست) را در زیر گزاره G (و یک F را در زیر G در ستون راهنما) قرار میدهیم.

نکتهای در مورد سایه زدن: در سرتاسر این قسمت، مقادیر ارزش مقدمات و نتیجه یک استدلال را سایهدار میکنیم. این ممکن میسازد تا به راحتی — با بررسی مقادیر ارزش سایهدارها — ببینیم که آیا یک سطر جدول ارزش کوتاهترِ کاملشده همهیِ مقدمات درست و نتیجه نادرست را دارد یا خیر. در ساخت جدول ارزش کوتاهتر، خواننده باید مقادیر ارزش مقدمات و نتیجه را در دایره قرار دهد.
از آنجایی که G در نتیجه نادرست است، G باید در مقدمه ۱ نادرست باشد.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
اکنون میکوشیم تا همه مقدمات را درست سازیم. به پیروی از راهبری II، ابتدا گزاره ساده F را در مقدمه ۲ درست میسازیم.

با توجه به درستی F در مقدمه ۲، بلافاصله F را در مقدمه ۱ درست میسازیم.

درستی F و نادرستی G موجب میشود مقدمه ۱، یعنی گزاره شرطی F⊃G، نادرست باشد.
گام ۴: آزمون اعتبار.
جدول ارزش کوتاهتر اکنون کامل شده است. آیا استدلال معتبر است یا نامعتبر؟
به راحتی میتوان دریافت که استدلال معتبر است، زیرا وقتی نتیجه نادرست است، مقدمات نمیتوانند همه درست باشند. گرچه مقدمه ۲، یعنی F، درست است، اما درستی F و نادرستی نتیجه، یعنی G، ایجاب میکند که مقدمه ۱، یعنی F⊃G، نادرست باشد. این استدلال همهیِ مقدماتِ درست را برای تنها ترکیبی از مقادیر ارزش ندارد که نتیجه بر اساس آن نادرست است. این ثابت میکند که استدلال نمیتواند نتیجه نادرست و همهیِ مقدمات درست داشته باشد، و این خود ثابت میکند که معتبر است.
همانطور که در مقدمه این قسمت گفته شد، و همانطور که در این مثال آشکارا میبینیم، جدول ارزش کوتاهتر برای یک استدلال معتبر با یک گزاره ساده بهعنوان نتیجه، بهضرورت دارای حداقل یک مقدمه نادرست است. زیرا، یک استدلال معتبر نمیتواند همهیِ مقدماتِ درست و یک نتیجه نادرست داشته باشد.
مثال ۲: یک استدلال مرکب که در آن نتیجه یک گزاره ساده است
اکنون STTT را با جزئیات گام به گام و با استفاده از استدلالی با پیچیدگی بیشتر از استدلال مثال ۱ توضیح خواهیم داد.
(P۱): (E ∨ F) ⊃ (G • H)
(P۲): (G ∨ H) ⊃I
(P۳): E
∴ I
از آنجا که این استدلال شامل پنج گزاره ساده متمایز است، جدول ارزش کامل آن دارای ۲۵ یا ۳۲ سطر خواهد بود. با استفاده از STTT، در یک جدول ارزش یک سطری تعیین میکنیم که آیا این استدلال معتبر است یا نامعتبر است.
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه گزاره ساده I است که تنها از یک راه نادرست است، هنگامی که I نادرست است. از آنجایی که هیچ مقدمهای نمیتواند به روشهای کمتری درست باشد، گامهای ۳C، ۲C ، و ۴ را ادامه میدهیم.
گام ۲C: نتیجه را نادرست سازید.
در گام ۲، ابتدا توسط راهبری I پیش میرویم
راهبری I : در صورت امکان، ابتدا گمارش مقادیر ارزش اجباری را به نتیجه یا مقدمه، همانطور که در گام ۱ تعیین شده است، انجام دهید.
تنها یک راه برای نادرست بودن نتیجه این استدلال وجود دارد: گزاره I باید نادرست باشد. بنابراین، ما میباید با قرار دادن یک F (نادرست) زیر گزاره I، گزاره I را نادرست کنیم.

وقتی یک مقدار ارزش به یک گزاره ساده گمارده، آن مقدار ارزش باید فوراً به آن گزاره ساده در هر جای دیگری که در استدلال رخ میدهد (و زیر آن گزاره ساده در ستون های راهنما) گمارده شود. گزاره I نیز در مقدمه ۲ رخ میدهد، بنابراین ما بلافاصله مقدار ارزش نادرست را به I در مقدمه ۲ (و همچنین به I در ستونهای راهنما) میگماریم.

مهم است بدانیم چرا این کار را انجام میدهیم. گزاره I نیز در مقدمه ۲ نادرست است زیرا یک سطر در یک جدول ارززش کوتاهتر — مانند یک سطر در یک جدول ارزش کامل — فقط ترکیب خاصی از مقادیر ارزش برای گزارههای ساده تشکیل دهنده استدلال (و مقادیر ارزش گزارههای مرکب شامل فقط از این گزارههای ساده) است. بنابراین، اگر یک گزاره، مانند I، در جایی از یک سطر معین نادرست باشد، همه رخدادهای آن گزاره در آن سطر باید دارای مقدار ارزش یکسانی باشند. به همین دلیل، وقتی به یک گزاره ساده در یک سطر در یک جدول ارزش کوتاهتر، یک مقدار ارزش میگماریم، بلافاصله همان مقدار ارزش را به آن گزاره ساده در تمام رخدادهای آن در آن سطر نیز میگماریم.
گام ۳C: تا جایی که ممکن است مقدمات را درست سازید.
اکنون که نتیجه نادرست شده است، لازم به یادآوری است که هدف ما از دنبالهِ-C این است که همه آن مقدماتِ مربوط به گمارش(های) مقادیر ارزش، که نتیجه(ها) را نادرست میسازند، درست سازیم. اگر این ممکن هست، آنگاه استدلال نامعتبر است؛ اگر ممکن نیست، استدلال معتبر است. در اجرای صحیح این روند، یا ثابت میکنیم که استدلال نامعتبر است یا ثابت میکنیم که استدلال معتبر است.
در این گام، ما راهبری II را به کار میگیریم، قاعدهای که تضمین میکند STTT را به سادهترین و کارآمدترین شکل ممکن اجرا میکنیم.
راهبری II: گمارش مقادیر ارزش اجباری به مقدماتی که گزارههای ساده یا نقیض گزارههای ساده هستند را پیش از گمارش مقادیر ارزش اجباری به مقدمات ترکیبیتر انجام دهید.
گمارش مقادیر-ارزش اجباری، یک گمارش مقدار ارزش به یک گزاره ساده یا مرکب است که ناگزیر در دایره سه گانه زیر باشد:
سرشت تابع–ارزشی گزارههای ساده و مرکب،
هدف(های) ما و/یا
گمارشهای مقادیرِ ارزش از پیش گماردهشده.
برای مثال، (ii) اولین هدف در گام ۲C ما را وامیدارد که تنها و فقط تنها آن گمارشهای مقدار ارزش را به گزارههای ساده در آن نتیجهای انجام دهیم که نتیجه را نادرست میسازد. از آنجایی که فقط یک راه برای نتیجه، یعنی گزاره ساده I، وجود دارد که نادرست باشد، ابتدا مقدار ارزش نادرست به گزاره ساده I را در همه رخدادهای آن میگماریم. هنگامی که این کار انجام شد، از آنجا که، (ii) هدف بعدی ما، در گام ۳C، درست سازی همه مقدمات است، گاهی وقتها در (iii) مقدار ارزش از پیش گمارده شده به گزارههای ساده در یک مقدمه، ما را وامیدارد تا مقدار ارزش خاصی را به سایر گزارههای ساده یا مرکب اختصاص دهیم تا در (ii) با توجه به (i)، یعنی سرشت تابع-ارزشی گزارههای مرکب، به هدف خود در درست ساختن آن مقدمه خاص برآییم.
با نگاه به راهبری II، میپرسیم آیا هر مقدمهای ساده است یا نقیض گزارههای ساده؟ در مثال ما جواب بله است. مقدمه ۳ گزاره ساده E است. بنابراین، توسط راهبری II مجبوریم، قبل از اینکه به سراغ گمارش مقدار ارزش اجباری به گزارههای مرکب برویم، ابتدا E را در مقدمه ۳ و در همه موارد دیگر آن درست سازیم. بنابراین، E را در مقدمه ۳ و در مقدمه ۱ (و در ستون راهنمای E) درست میسازیم.

با توجه به اینکه E درست و I نادرست است، آیا گمارش مقدار ارزش اجباری دیگری وجود دارد؟ پاسخ آری است و دو مورد هست. از آنجا که E درست است، مجبوریم E∨F را درست سازیم، زیرا یک فصلی درست است وقتی که حداقل یکی از فصلهای آن درست باشد. با توجه به اینکه I نادرست است، ما مجبوریم که G⊃H را نادرست سازیم، زیرا مقدمه ۲، یعنی (G∨H)⊃I یک شرطی با تالی نادرست است، که تنها در صورتی درست است که مقدم آن نادرست باشد. از آنجا که این دو گمارش مقدار ارزش - به مقدمه ۱ و مقدمه ۲ - به یک اندازه اجباری هستند، ما باید راهبری IV را اعمال کنیم.
راهبری IV: اگر گمارش مقادیر ارزش به دو یا چند مقدمه به طور معادل اجباری است (مثلاً به دو گزاره ساده) یا به همان اندازه غیراجباری است، ابتدا گمارش مقادیر ارزش در سمت چپترین را انجام دهید.
با استفاده از راهبری IV، با اجباریترین گمارش مقدار ارزش از سمت چپ، به مقدمه ۱، آغاز میکنیم. از آنجا که E در مقدمه ۱ درست است، مقدمِ مقدمه ۱، یعنی E∨F، نیز درست است. بنابراین یک T را زیر گُوِه (رابط فصل) E∨F قرار میدهیم.

با توجه به اینکه E∨F درست است، مقدمه ۱ تنها در صورتی درست است که تالی آن، G•H، درست باشد. بنابراین یک T (درست) را زیر رابط عطف در G•H قرار میدهیم.

بخشی از گمارش مقدار ارزش اجباری به این معنی است که برای اجرای گام ۳C، مقدار ارزش یک گزاره مرکب گمارش مقدار ارزش به گزارههای مرکب و/یا ساده را ومیدارد (به بند (الف) مراجعه کنید). برای مثال، از آنجایی که شرطی (E∨F)⊃(G•H) دارای مقدم درست است، تنها وقتی درست است که تالی آن، ترکیب عطفی G•H، درست باشد. به نوبه خود، ترکیب عطفی G•H تنها وقتیی درست است که هر دو عطف آن، یعنی گزاره ساده G و گزاره ساده H، درست باشند. مقدار ارزش گزارههای مرکب، گمارشهای مقدار ارزش را به روشهای زیر تحمیل میکنند.
| ترکیب عطفی | G•H درست است | G را درست و H را درست سازید. |
| ترکیب فصلی | G∨H نادرست است | G را نادرست و H را نادرست سازید. |
| ترکیب شرطی | G⊃H نادرست است | G را درست و H را نادرست سازید. |
| نقیض | ~G درست است ا~G نادرست است | G را نادرست سازید. G را درست سازید. |
بنابراین، ما اکنون مجبوریم G را درست و H را در ترکیب عطفی G•H (و در ستونهای راهنما G و H) درست سازیم.

با توجه به اینکه تالی مقدمه ۱ اکنون درست و مقدمه ۱ درست است؛ بنابراین یک T را زیر نعل اسبی (رابط شرطی) در مقدمه ۱ قرار می دهیم.

مثل همیشه، وقتی مقادیر ارزش را به گزارههای ساده G و H گماردیم، همان گمارشهای مقادیر ارزش را به G و H در همه موارد آنها انجام میدهیم. بنابراین ما G و H هر دو را در مقدمِ مقدمه ۲، یعنی G∨H درست میسازیم.

اگر G و H هر دو درست باشند، فصلی G∨H درست است. بنابراین یک T را زیر گُوِه (رابط فصل) G∨H در مقدمه ۲ قرار میدهیم.
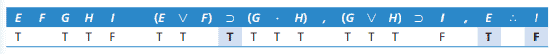
مقدمه ۲، یعنی شرطی (G∨H)⊃I، اکنون یک مقدم درست و یک تالی نادرست دارد که آن را نادرست میکند.

ما جدول ارزش کوتاهتر خود را مطابق با گامهای ۲C و ۳C تکمیل کردهایم و اکنون برای گام ۴ آماده هستیم. باید بگوییم که، ما به گزاره ساده F مقدار ارزشی نگماردهایم، چراکه بدان نیاز نبود.➥۱۱
گام ۴: آزمون اعتبار.
آیا استدلال معتبر است یا نامعتبر؟ از جدول ارزش کامل یک سطری به راحتی میتوان دریافت که استدلال معتبر است، زیرا مقدمات نمیتوانند برای هر گمارش مقدار ارزش که در آن نتیجه نادرست است درست باشند. تنها یک گمارش مقدار ارزش وجود دارد که نتیجه در مورد آن نادرست است (یعنی وقتی I نادرست است)، و تنها یک گمارشِ مقدار ارزش وجود دارد که در آن مقدمه ۳ درست است (یعنی وقتی E درست است). این گمارشهای مقدار ارزش به نوبه خود تالی مقدمه ۱ را ومیدارد که درست باشد، که به نوبه خود G و H را مجبور میکند هر دو درست باشند. این گمارشهای اجباری مقدار ارزش، مقدمِ مقدمه ۲، یعنی G∨H را درست میکند، که با توجه به نادرستی I، مقدمه ۲، (G∨H)⊃I، نادرست میشود. بنابراین، اگرچه میتوانیم با توجه به نادرست بودن نتیجه، مقدمه ۳ و مقدمه ۱ را درست کنیم، نمیتوانیم مقدمه ۲ را درست کنیم.➥۱۲
۱۲- اگر از راهبری IV پیروی نمیکردیم و در عوض سعی میکردیم مقدمه ۲ درست باشد، G∨H را در مقدمه ۲ با نادرست کردن G و H نادرست میکردیم. اگر G و H در مقدمه ۱ نادرست باشند، چون E درست است، شرطی (E∨F)⊃(G•H) نادرست خواهد بود. این ثابت میکند که استدلال نمیتواند همه مقدمات درس بنابراین، در مورد تنها گمارش مقادیر ارزش که نتیجه را نادرست میکند، مقدمات همه درست نیستند. این ثابت میکند که این استدلال نمیتواند نتیجه نادرست و همه مقدمات درست داشته باشد که این اعتبار آن را ثابت میکند.➥۱۳
کار ما به سرانجام رسیده است و به جای ساختن جدول ارزش کامل ۳۲ سطری، STTT را در یک سطر اجرا کردیم و مشخص کردیم که استدلال معتبر است. البته برهان این استدلال تنها از پنج استنتاج (Add. M.P.، Simp.، Add.، و M.P.) تشکیل شده است، STTT بیشتر از برهان زمان نمیبرد. برای استدلالهایی که نیاز به برهانهای دشوارتر و طولانیتر دارند، STTT معمولاً بسیار کارآمدتر خواهد بود. وقتی تلاش نافرجام برای برهان یک استدلال نامعتبر است، STTT تقریباً همیشه بسیار کارآمدتر از CTTM است.➥۱۴
مثال ۳: یک استدلال که در آن نتیجه یک گزاره شرطی است
مثالهای ۱ و ۲ نشان میدهند که در STTT وقتی نتیجهیِ یک استدلال یک گزاره ساده (یا نقیض یک گزاره ساده) باشد چقدر کارآمد است. اکنون خواهیم دید که اگر در STTT نتیجه استدلال یک گزاره مرکب پیچیدهتر باشد، بقسمی که فقط برای یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن نادرست باشد، به همان اندازه کارآمد است. استدلال زیر را در نظر بگیرید.
(P۱): (B ⊃ W) • (G ⊃ ~S)
(P۲): (~B • ~G) ⊃ (C • P)
(P۳): ~W
(P۴): P
∴ C ⊃ ~G
از آنجا که این استدلال شامل شش گزاره ساده متمایز است، جدول ارزش کامل آن ۲۶ یا ۶۴ سطر خواهد داشت. با این حال، با استفاده از STTT، در یک سطر معین میکنیم که آیا این استدلال معتبر است یا نامعتبر است.
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
با توجه به اینکه نتیجه استدلال، C⊃~G، فقط برای یک ترکیب از مقادیر ارزش برای C و G نادرست است (یعنی زمانی که C درست است و G درست است)، ما با گامهای ۳C، ۲C ، و ۴ ادامه میدهیم و میتوانیم آزمون اعتبار بسیار آسان و خیلی سریع را در یک جدول ارزش کوتاهتر یک سطری به سرانجام برسانیم.
گام ۲C: نتیجه را نادرست سازید.
در اجرای گام ۲، راهبری I را دنبال میکنیم و ابتدا گمارش اجباری مقادیر ارزش را برای نتیجه انجام میدهیم. از آنجایی که عملگر منطقی اصلی نتیجه، یعنی C⊃~G، نعل اسبی (رابط شرط) است، ابتدا یک F را زیر نعل اسبی در C⊃~G قرار میدهیم.

از آنجا که نتیجه یک گزاره شرطی است، با درست ساختن مقدم آن، یعنی C، و نادرست ساختن تالی آن، یعنی ~G، آن را نادرست میکنیم.

این گمارشهای اجباری مقدار ارزش، گمارش T (درست) را به G نیز وامیدارد.➥۱۵

در انجام این گمارشهای مقدار ارزش به C و G در نتیجه، باید همان گمارشهای ارزش به C و G را در همه موارد آنها انجام دهیم. C در مقدمه ۲ و G در مقدمه ۱ و در مقدمه ۲ رخ میدهد.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
به پیروی از راهبری II، ما ابتدا گمارش اجباری مقدار ارزش را به مقدماتی گمارده که گزارههای ساده یا نقیض گزارههای ساده هستند. از آنجایی که ما مجبوریم برای نقیض یک گزاره ساده در مقدمه ۳ و به یک گزاره ساده در مقدمه ۴ یک گمارش مقدار ارزش انجام دهیم، راهبری III را به کار میزنیم و اول ~W را در مقدمه ۳ درست میسازیم.

این گمارش مقدار ارزش ، W را وامیدارد تا نادرست باشد.

اکنون باید مقدار ارزش نادرست را به W در هر جای دیگری که رخ دهد بگماریم. W در مقدمه ۱ رخ میدهد، بنابراین ما W را در مقدمه ۱ نادرست میکنیم.

در ادامه پیرو راهبری II، از ~W به سمت راست حرکت میکنیم و گمارش اجباری مقدار ارزشِ درست را به گزاره ساده P را در مقدمه ۴ انجام میدهیم.

با توجه به اینکه P در مقدمه ۴ درست است، باید فوراً در تنها رخداد دیگر آن، در مقدمه ۲، درست شود.

این گمارش مقدار ارزش ، C•P را در مقدمه ۲ درست میکند.

و از آنجایی که C•P درست است، کل شرطی در مقدمه ۲، یعنی (~B•~G)⊃(C•P) صرف نظر از مقدار ارزشِ مقدمِ شرطی، یعنی ~B•~G درست است.

این به این معنی است که B میتواند هر دو مقدار ارزش را در مقدمه ۲ داشته باشد. B نیز در مقدمه ۱ رخ میدهد. آیا مجبوریم یک مقدار ارزش خاصی را به B در مقدمه ۱ اختصاص دهیم؟ پاسخ آری است. از آنجایی که مقدمه ۱ یک ترکیب عطفی است، تنها در صورتی درست است که هر دو عطف آن درست باشند. عطف سمت چپ مقدمه ۱، یعنی B⊃W، شرطی است که W تالی آن نادرست است. بنابراین ما مجبوریم B را نادرست کنیم تا B⊃W درست شود.

از آنجا که B در مقدمه ۱ نادرست است، باید آن را در تنها رخداد دیگر آن، در مقدمه ۲، نادرست کنیم.

باز هم، از آنجا که مقدمه ۱ یک ترکیب عطفی است، تنها وقتی درست است که عطف راست آن نیز درست باشد. عطف راست مقدمه ۱ شرطی G⊃~S است و مقدمِ آن، گزاره G، درست است. بنابراین، برای درست کردن G⊃~S، ما باید تالی آن، ~S را درست کنیم، که به نوبه خود ما را مجبور میکند که S را نادرست کنیم.

اکنون که هر دو عطف مقدمه ۱ درست است، با قرار دادن T در زیر نقطه (رابط عطف)، مقدمه ۱ را درست میکنیم.

از آنجا که در مقدمه ۲ یک مقدار ارزش به B گماردهایم، باید مقدار ارزش ~B•~G را در مقدمه ۲ حساب کنیم.

جدول ارزش کوتاهتر اکنون کامل است، زیرا در گمارشهای اجبارییِ مقدارِ ارزش به نتیجه و مقدمات ۳، ۴، ۲، و ۱ (به ترتیب)، همه مقدمات درست و نتیجه نادرست شده است.
گام ۴: آزمون اعتبار.
گام ۴ به ما میگوید که اگر برای هر نتیجهیِ نادرست، کمارشهای مقدار-ارزش بهطور سازگار همه مقدمات را درست میکنند، آنگاه باید اجرا پایان پذیرد، زیرا ثابت شده است که استدلال نامعتبر است. در نادرست ساختن نتیجه و درست ساختن مقدمه ۳ و مقدمه ۴، مقدمه ۲ درست شد و ما مجبور شدیم B را نادرست و نیز S را نادرست کنیم تا مقدمه ۱ درست باشد. در این گمارشهای مقدار-ارزش، همه مقدمات درست و نتیجه نادرست است، که این ثابت میکند استدلال نامعتبر است. ما ثابت کردیم استدلال نامعتبر است و این را با نشان دادن اینکه، این استدلال میتواند دارای همهیِ مقدمات درست و نتیجهیِ نادرست باشد، انجام دادیم. گمارش مقادیر ارزش به گزارههای ساده که در زیر آمده نشان میدهد در چه ترکیب از مقادیر ارزش همه مقدمات درست و نتیجه نادرست است.

مثال ۴: یک استدلال که در آن نتیجه یک ترکیب فصلی است
مثال چهارم ما استدلال زیر است که نتیجهیِ آن یک ترکیب فصلی است
(P۱): (X ∨ Y) ⊃ (X • Y)
(P۲): ~(X ∨ Y)
∴ ~X ∨ ~Y
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
از آنجایی که نتیجه، ~X∨~Y، تنها در یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن نادرست است (یعنی زمانی که X درست است و Y درست است)، ما با گامهای ۳C، ۲C ، و ۴ ادامه میدهیم و با نادرست کردن نتیجه شروع میکنیم.
گام ۲C: نتیجه را نادرست سازید.
در اجرای گام ۲، راهبری I را دنبال میکنیم و ابتدا گمارش اجباری مقادیر ارزش را برای نتیجه انجام میدهیم. از آنجایی که نتیجه ترکیب فصلی ~X∨~Y است، ابتدا یک F را زیر گُوِه (رابط فصل) قرار میدهیم.

ترکیب فصلی ~X∨~Y فقط وقتی نادرست است که هر دو فصل آن یعنی ~X و ~Y نادرست باشند.

این گمارش مقدار ارزش به ~X و ~Y ما را وامیدارد تا X و Y هر دو را درست سازیم.

از آنجایی که X را درست و Y را در نتیجه درست ساختهایم، باید همان گمارشهای مقدار ارزش را به X و Y در هر جای دیگری که در استدلال رخ میدهند، انجام دهیم. X و Y هر کدام سه رخداد دیگر در مقدمات استدلال دارند.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
اکنون ما باید به دنبال گمارش اجباری مقادیر ارزش به گزارههای ساده در مقدمات بگردیم. با این حال، در این مورد، گمارشهای اجباری مقدار ارزش به X و Y در نتیجه، تمام گمارشهای مقدار ارزش به گزارههای ساده، X و Y را در مقدمات تکمیل کردهاند. بنابراین، راهبری IV را به کار میزنیم و مقدار ارزش مقدمه سمتِ چپترین، یعنی مقدمه ۱، را تعیین میکنیم. با توجه به اینکه X درست است و Y درست است، مقدمِ مقدمه ۱، یعنی ~X∨~Y، درست است.

و از آنجایی که X درست است و Y درست است، تالی مقدمه ۱، یعنی X•Y، درست است.

در مقدمه ۲، X∨Y درست است زیرا هر دو فصل آن درست هستند.

با توجه به اینکه X∨Y در مقدمه ۲ درست است، مقدمه ۲، یعنی ~(X∨Y)، نادرست است.

گام ۴: آزمون اعتبار.
نتیجه این استدلال، ~X∨~Y، تنها در صورتی نادرست است که X درست و Y درست باشد. در این ترکیب از مقادیر ارزش برای X و Y، مقدمه ۱ درست است، اما مقدمه ۲ نادرست است. این نشان میدهد این استدلال نمیتواند همهیِ مقدمات درست و نتیجه نادرست را داشته باشد، بنابراین ثابت میشود استدلال معتبر است.
د. نتیجههایی که در ترکیبهای چندگانه مقدار-ارزش نادرست هستند
تا اینجا، ما STTT را برای چهار استدلال بهکار بردهایم، که همه آنها نتایجی دارند که تنها در یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیلدهندهشان، نادرست هستند. زمانی که تنها یک گمارش از مقادیر ارزش به گزارههای ساده نتیجه، نتیجه را نادرست میکند، STTT بیشترین کارآمدی را دارد. در تمام این موارد، گامهای ۳C، ۲C ، و ۴ را اجرا میکنیم و از STTT برای ساختن یک جدول ارزش کوتاهتر یک سطری بهره خواهیم برد.
با این حال، زمانی که نتیجه یک استدلال در مورد ترکیبهای چندگانه مقادیر ارزش در گزارههای ساده تشکیلدهنده آن نادرست است، وضعیت تا حدودی پیچیدهتر میشود. ما ممکن است نیاز به اجرای STTT برای چندین سطر از یک جدول ارزش کوتاهتر داشته باشیم.➥۱۶
۱۶- اگر هیچ مقدمهای از راههای کمتر از نادرست بودن نتیجه درست نباشد، اگر برای اولین نتیجه نادرست، همه مقدمات درست باشند، نیازی به بررسی چند نتیجه نادرست نیست. در آن و تنها در آن مورد، ما نیازی به بررسی هیچ یک از نتایج نادرست دیگر نداریم، زیرا با استفاده از گمارش مقدار ارزش برای اولین نتیجهی نادرست ثابت میکنیم که استدلال نامعتبر است.برای به حداکثر رساندن کارایی در چنین مواردی، در گام ۱ تعیین میکنیم که آیا دنباله-C یا دنباله-P در STTT باید اجرا شود، به این ترتیب که معین میکنیم کدام مقدمه، به راههای کمتری نسبت به راههایی که نتیجه نادرست است، درست است.
در این بخش، سه استدلال که در پی میآیند را با استفاده از STTT خواهیم آزمود و نشان میدهیم که چگونه گام ۱ تعیین میکند که آیا از دنباله-C یا دنباله-P استفاده شود.
مثال ۵: استدلالی که در آن نتیجه ترکیب عطفی از گزارههای ساده است.
مثال ۶: استدلالی که در آن نتیجه ترکیب عطفی از گزارههای ساده است.
مثال ۷: استدلالی که در آن نتیجه ترکیب دو شرطی از گزارههای ساده است
در مثال ۶ نشان خواهیم داد که چه زمانی و چگونه گامهای ۳P، ۲P ، و باید برای به حداکثر رساندن کارایی مورد استفاده قرار گیرند.
مثال ۵: استدلالی که در آن نتیجه ترکیب عطفی از گزارههای ساده است
نتیجه در استدلال زیر یک عطفی است.
(P۱): M ∨ N
(P۲): (M ∨ N) ⊃O
(P۳): (M ∨ N) ⊃P
∴ O • P
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه، O•P، در مورد سه ترکیب از مقادیر ارزش: F•T، T•F، و F•F برای گزارههای ساده تشکیل دهنده آن، O و P نادرست. با این حال، هر مقدمه حداقل از سه راه درست است: مقدمه ۱ از سه راه درست است (یعنی F∨T، T∨F، T∨T)، مقدمه ۲ از پنج راه درست است، و مقدمه ۳ از پنج راه درست است. از آنجا که هیچ مقدمهای از راههای کمتر از نادرست بودن نتیجه درست نیست، گامهای ۳C، ۲C ، و ۴ را ادامه میدهیم.
گام ۲C: نتیجه را نادرست سازید.
در نادرست ساختن یک نتیجه برای ترکیبهای چندگانه مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن، یا در درست ساختن یک مقدمه برای ترکیبهای چندگانه مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن، ما همیشه طبق راهبری V پیش خواهیم رفت:
راهبری V: در ساخت یک جدول ارزش کوتاه چند سطری، یک نتیجه نادرست (یا یک مقدمه درست) بسازید (الف) فقط با استفاده از آن دسته از ترکیبات مقادیر ارزش که مقدار ارزش دلخواه را برای آن گزاره مرکب بهدست میدهند، و (ب) آنها را به ترتیبی مرتب کنید که در یک جدول ارزش تمامشده پدیدار میشوند (به بخش ۹.۶ - آزمون اعتبار با جدول ارزش - مراجعه کنید). برای مثال، برای یک گزاره مرکب متشکل از دو گزاره ساده، به ترتیب، فقط از ترکیباتی که TT، TF، و FT و FF استفاده کنید که مقدار ارزش مورد نظر را برای عبارت-گزارهای بهدست میدهند.
از فصل ۹ (قسمت ۹.۶) روش ساختن جداول ارزش کامل، و نحوه تعیین تعداد سطرها و نحوه پر کردن ستونهای راهنما با T و F را به یاد بیاورید. در آنجا دیدیم که برای یک گزاره مرکب که از n گزاره ساده تشکیل شده است، ۲n ترکیب مقداز ارزش وجود دارد. بنابراین، برای یک گزاره مرکب متشکل از دو گزاره ساده، ۲۲ یا ۴ ترکیب مقداز ارزش وجود دارد: TT، TF، FT، و FF. بطور مشابه، برای یک گزاره مرکب متشکل از سه گزاره ساده، ۲۳ یا ۸ ترکیب مقداز ارزش وجود دارد. و برای یک گزاره مرکب متشکل از چهار گزاره ساده متمایز، ۲۴ یا ۱۶ ترکیب مقداز ارزش وجود دارد و مانند آنها.
راهبری V ما را به ساختن (الف) فقط آن دسته از ترکیبهای مقدار ارزش را هدایت میکند که مقدار ارزش مورد نظر را برای یک گزاره مرکب به دست میدهند، و ما را به ساختن (ب) به ترتیبی که در یک جدول ارزش کامل نشان داده خواهند شد، هدایت میکند. به عنوان مثال، فرض کنید که نتیجه یک استدلال، Q•R است، و ما میخواهیم آن را نادرست کنیم. چهار ترکیب مقدار ارزش برای دو گزاره ساده، Q و R وجود دارد: T•T، T•F F•T، و F•F. با این حال، ما یک جدول ارزش چند سطری را فقط برای ترکیبهای T•F، F•T و F•F (به ترتیب) درست میسازیم ، زیرا فقط آنها عطفی Q•R را نادرست میکنند (یعنی T•T را حذف میکنیم، زیرا Q•R درست است اگر Q درست باشد و R درست باشد).

همینطور، اگر یک جدول ارزش چند سطری برای مقدمه H•(I⊃J) بسازیم، که شامل سه گزاره ساده است، هشت ترکیب مقدار ارزش برای H، I و J وجود دارد: TTT، TTF، TFT، TFF، FTT. ، FTF، FFT و FFF. به پیروی راهبری V، ما یک سطر جدول ارزش را فقط برای آن دسته از ترکیبات مقدار ارزش برای گزارههای ساده H، I، و J میسازیم که این مقدمه را درست میکنند. از هشت ترکیب ممکن از مقادیر ارزش برای این سه گزاره ساده، تنها سه مورد (یعنی TTT، TFT، TFF) گزاره مرکب H•(I⊃J) را درست میکنند. بنابراین، ما سه سطر را برای مقدمه H•(I⊃J) میسازیم، با استفاده از این سه ترکیب مقدار ارزش (به ترتیب) - TTT، TFT، TFF - زیرا این ترتیبی است که آنها در یک جدول ارزش کامل ظاهر میشوند.

ما پنج ترکیب دیگر (یعنی TTF، FTT، FTF، FFT، و FFF) را حذف میکنیم زیرا H•(I⊃J) در این ترکیبهای مقدار ارزش نادرست است.
در کاربرد راهبری V به استدلال در دست، از آنجا که نتیجه عطفی O•P برای T•T نادرست نیست، جدول ارزش کوتاهتر سه سطری زیر را برای سه ترکیب T•F، F•T و F•F درست میکنیم.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
در یک جدول ارزش کوتاهتر چند سطری، گام ۳C را با در نظر گرفتن هر یک از مجموعهای از گمارشهای مقدار ارزش که تحت آن نتیجه نادرست است، اجرا میکنیم. اگر برای هر نتیجه نادرستی، بتوانیم همه مقدمات را درست کنیم، اجرا را پایان میدهیم، زیرا در آن صورت ثابت کردهایم که استدلال نامعتبر است. با این حال، برای اثبات اعتبار یک استدلال از راه گام ۳C، باید همه ترکیبهای مقادیر ارزش را برای گزارههای سادهای که نتیجه را نادرست میکنند، در نظر بگیریم، و باید برای هر یک از این ترکیبها نشان دهیم که استدلال نمیتواند همه مقدمات درست را داشته باشد. اگر یک استدلال معتبر باشد، حداقل یک مقدمه نادرست اجباری برای هر نتیجه نادرست وجود خواهد داشت.
از آنجایی که نتیجه این استدلال، O•P، از سه راه نادرست است، ما با اولین گمارش مقدار ارزش آغاز میکنیم و گام ۳C را با گمارش مقدار ارزش اجباری اجرا میکنیم تا زمانی که یا موفق به درست سازی همه مقدمات، یا مجبور به ایجاد یک مقدمه نادرست، شویم. در این صورت به سطر بعدی در این جدول ارزش سه سطری میرویم.
با توجه به اینکه در سطر اول جدول ارزش کوتاهتر، O درست و P نادرست است، ما بطور سازگار آن مقادیر ارزش را به ترتیب به O و P، در هر جای دیگری که رخ میدهند، نسبت میدهیم. O بعنوان تالی مقدمه ۲ رخ میدهد، بنابراین ما O را در آنجا درست میسازیم. P به عنوان تالی مقدمه ۳ رخ میدهد، بنابراین ما در آنجا P را نادرست میسازیم.

با توجه به اینکه O، تالی مقدمه ۲ درست است، این موجب میشود که مقدمه ۲ درست شود.

گام ۳C اکنون مستلزم آن است تا بکوشیم همه مقدمات را تحت این گمارش مقدار ارزش درست کنیم. در این فصلی، تنها یک گمارش مقدار ارزش اجباری وجود دارد: با توجه به نادرست بودن P در مقدمه ۳، مقدمه ۳ تنها در صورتی درست است که مقدم آن، M∨N، نادرست باشد.

نادرستی M∨N در مقدمه ۳ ما را مجبور میکند که M و N را در مقدمه ۳ نادرست کنیم، که این موجب میشود مقدمه ۳ درست شود.

از آنجا که M و N هر دو در مقدمه ۳ نادرست هستند، باید هر جا که رخ دهند نادرست باشند. از آنجا که M و N هر دو در مقدمه ۱ و در مقدمه ۲ رخ میدهند، در گام بعد، M و N را در هر دو مقدمه نادرست میسازیم.

نادرست بودن M و N هر دو در مقدمههای ۱ و ۲ باعث نادرست بودن M∨N در هر دوی این مقدمات میشود.

سطر ۱ در جدول ارزش کوتاهتر اکنون کامل است. درستی O و نادرستی P مقدمه ۲ را درست میکند و M و N را مجبور میکند هر دو نادرست باشند تا مقدمه ۳ درست باشد. این گمارش مقدار ارزش، مقدمه ۱ را نادرست میکند، که نشان میدهد وقتی O درست و P نادرست است، همه مقدمات نمی توانند درست باشند.
از آنجا که نتوانستیم همه مقدمات را برای اولین نتیجه نادرست درست سازیم، به سطر ۲ میرویم و نادرست را به O و درست را به P میگماریم. درستی P موجب میشود که مقدمه ۳ درست باشد.

نادرست بودن O در مقدمه ۲، برای ارزش مقدمه ۲، مستلزم آن است که مقدمِ مقدمه ۲، یعنی M∨N، نادرست باشد. باز هم، این بدان معنی است که M∨N در هر جای دیگری که رخ دهد نادرست است. مقدمه ۲ و ۳ بازهم درست هستند، ولی مقدمه ۱ هم باز نادرست است.

قبل از اینکه به آخرین سطر بپردازیم، باید بدانیم که تا اینجا نه اعتبار و نه بیاعتباری ثابت نشده است. ممکن است سطر آخر جدول ارزش سه سطری ما بتواند همه مقدمات درست و یک نتیجه نادرست داشته باشد، که در این صورت استدلال نامعتبر باشد. همچنین ممکن است در این آخرین حالت از نتیجهیِ نادرست، درستی همه مقدمات ممکن نباشد، که در این حالت استدلال معتبر خواهد بود. این بدان معنی است که تا آنجا که ما از این ترکیب فصلی میدانیم، این استدلال میتواند معتبر یا نامعتبر باشد. برای تعیین معتبر یا نامعتبر بودن استدلال، باید مقادیر ارزش مقدمات، وقتی که O نادرست و P نادرست است، را هم تعیین کنیم.

بار دیگر، نادرستی O در مقدمه ۲ برای درستی مقدمه ۲، مستلزم آن است که مقدمِ مقدمه ۲، M∨N، نادرست باشد؛ که نیز، این بدان معنی است که M∨N در هر جای دیگر که رخ دهد نادرست است. مقدمه ۲ و ۳ دوباره درست است، ولی مقدمه ۱ دوباره نادرست است.

سطر ۳ نشان میدهد که گرچه مقدمات ۲ و ۳ میتوانند، وقتی O نادرست و P نادرست است، درست باشند، ولی مقدمه ۱ نمیتواند در آن گمارشهای مقدار ارزش درست باشد.
گام ۴: آزمون اعتبار.
با توجه به اینکه این سه سطر همهیِ ترکیبهای ممکنِ مقادیر ارزش را برای O و P، که در آن نتیجه نادرست است، دربر میگیرد، پس ثابت کردهایم، که برای هر ترکیبی از مقادیر ارزش برای گزارههای ساده استدلال، مقدمات نمیتوانند همگی درست و نتیجه نادرست باشد. این ثابت میکند که این استدلال معتبر است.
مثال ۶: استدلالی که در آن نتیجه ترکیب عطفی از گزاره های ساده است
مانند مثال ۵، استدلال زیر یک نتیجه عطفی دارد.
(P۱): J ∨ K
(P۲): ~J
(P۳): G ⊃ H
(P۴): G
∴ H • K
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه، H•K، در سه ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن، H و K نادرست است.

آیا هر یک از مقدمات از کمتر از سه راه درست است؟ آری چنین است. مقدمه ۲ تنها از یک راه درست است (یعنی اگر J نادرست باشد) و مقده ۴ فقط از یک راه درست است (یعنی G درست است). بنابراین، گامهای ۳P، ۲P، و ۴ (یعنی دنباله-P) را اجرا می کنیم و ابتدا همه مقدمات را درست میسازیم. این کار را به این دلیل انجام میدهیم که اگر با گام ۲C شروع کنیم و استدلال معتبر باشد، باید هر سه نتیجه نادرست را بررسی میکردیم. اما اگر با گام ۲P شروع کنیم، فقط باید یک جدول ارزش کوتاهتر یک سطری بسازیم و آن را بررسی کنیم. گامهای ۲ و ۳ و دنباله-C و دنباله-P برای به حداکثر رساندن کارایی STTT با اطمینان از اجرای STTT در کمترین تعداد سطرها تدوین شدهاند.
گام ۲P: همه مقدمات را درست بسازید.
درست ساختن همهیِ مقدمات را با گمارش مقادیر ارزش اجباری آغاز میکنیم. با استفاده از راهبری II، ابتدا به دنبال مقدماتی میگردیم که گزارههای ساده یا نقیض گزارههای ساده باشند. دو گمارش اجباری مقدار ارزش این چنینی، در مقدمه ۲ (~J) و در مقدمه ۴ (G)، وجود دارد. بنابراین راهبری IV را بهکار میزنیم و با انجام دادن گمارش اجباری مقدار ارزش به سمت چپترین، یعنی ابتدا به مقدمه ۲ آغاز میکنیم.

مقدمه ۲، ~J، فقط در صورتی درست است که J نادرست باشد، بنابراین ما J را نادرست میکنیم.

با ادامه راهبری II، اکنون مقدمه ۴ را با درست کردن G درست میسازیم.

در گام بعد، G را در هر جای دیگری که در استدلال وجود دارد، درست میسازیم. G مقدمِ مقدمه ۳ است، بنابراین G را در آنجا درست میسازیم.

با استفاده از راهبری IV، با گمارش اجباری مقادیر ارزش که با سمت چپترین مقدمه شروع میشوند، ادامه میدهیم. از آنجا که هدف ما در ۲P درست سازی همه مقدمات است، از آنجایی که J نادرست است، با درست کردن K، مقدمه ۱ را درست میکنیم و یک T را زیر گوه J∨K قرار میدهیم.

ما اکنون مجبوریم بطور سازگار مقدار T (درست) را، هر جا K رخ دهد، به K بگماریم. از آنجا که K در نتیجه نیز وجود دارد، K را در نتیجه درست میسازیم.

با ادامه راهبری II، اکنون به سمت راست به سوی مقدمه ۳ میرویم. با توجه به اینکه G درست است، باید H را درست کنیم تا G⊃H درست باشد.

از آنجا که H در مقدمه ۳ درست است، باید در نتیجه نیز درست باشد.

با توجه به اینکه H درست و نیز K درست است، نتیجه، یعنی H•K، درست است.

اکنون جدول ارزش کوتاهتر کامل شده است.
گام ۳P: تنتیجه را نادرست بسازید.
آشکار است که نمیتوان نتیجه را نادرست کرد، زیرا در تنها ترکیب از مقادیر ارزش برای گزارههای ساده که همه مقدمات را درست میکنند، درست است. به ترتیب، J به اجبار نادرست، G به اجبار درست، K به اجبار درست، و سرانجام، H به اجبار درست شدهاند.
گام ۴: آزمون اعتبار.
در مورد تنها ترکیبی از مقادیر ارزش برای گزارههای ساده تشکیلدهنده که مقدمات آن همه درست است، نتیجه نیز درست است. این ثابت میکند که استدلال معتبر است، زیرا ثابت میکند که استدلال نمیتواند همه مقدمات درست و نتیجه نادرست داشته باشد.
مثال ۷: استدلالی که در آن نتیجه یک دو شرطی از گزاره های ساده است
سرانجام، استدلال زیر را در نظر بگیرید که نتیجه آن یک دو شرطی است.
(P۱): T • (U ∨ V)
(P۲): T ⊃ [U ⊃ (W • X)]
(P۳): (T • V) ⊃ ~ (W ∨ X)
∴ W ≡ X
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه، W≡X، در دو ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن نادرست است: W درست است و X نادرست است، W نادرست است و X درست است. آیا هر مقدمه فقط برای یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده آن درست است؟ مقدمه ۱ عطف T•(U∨M) است که به سه راه درست است: T درست است، U درست است و V درست است. T درست است، U درست است و V نادرست است. و T درست است، U نادرست است و V درست است. مقدمه ۲ از چند راه درست است، و همین نیز در مورد مقدمه ۳ برقرار است. بنابراین، گامهای ۳C، ۲C ، و ۴ را ادامه می دهیم.
گام ۲C: نتیجه را نادرست سازید.
ابتدا یک F را در زیر سه-خطی نتیجه دوشرطی، یعنی W≡X، قرار میدهیم.

در گام بعد، با پیروی از راهبری V، هر ترکیب از مقادیر ارزش را ایجاد میکنیم که در آن نتیجه نادرست است. این کار را با برشمردن چهار ترکیب ممکن انجام میدهیم — T≡T، T≡F، F≡T، و F≡F — و سپس آن ترکیبهایی را حذف میکنیم که نتیجه را نادرست نمیکنند. روند راهبری V به ترتیب: T≡F و F≡T را به دست میدهد.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
مانند همه جداول ارزش کوتاه چند سطری، با اولین ترکیب مقادیر ارزش که نتیجه آن نادرست است آغاز میکنیم (سطر ۱): W درست است و X نادرست است. با کارزدن این گمارشهای مقدار ارزش به W و X در بقیه استدلال، گمارشهای مقدار ارزش زیر را در مقدمات ۲ و ۳ خواهیم داشت.

راهبری II کاربرد ندارد زیرا هیچ مقدمهای وجود ندارد که گزارههای ساده یا نقیض گزارههای ساده باشند. بنابراین، راهبری IV را به کار میزنیم و با اجبار گمارش مقدار ارزش از سمت چپتری آغاز میکنیم. از آنجا که مقدمه ۱ فقط در صورتی درست است که هر دو عطف آن درست باشد، T را درست می کنیم و T را زیر گوه (رابط فصل) U∨V قرار میدهیم.

با توجه به اینکه T درست است، باید T را در مقدمه ۲ و در مقدمه ۳ درست سازیم.

در این ترکیب فصلی، دو گمارش اجباری مقدار ارزش وجود دارد، یکی در مقدمه ۲ و دیگری در مقدمه ۳. با استفاده از راهبری IV، ما گمارش اجباری مقدار ارزش را در سمت چپترین انجام میدهیم. از آنجایی که T به عنوان مقدمِ مقدمه ۲ درست است، نتیجه، U⊃(W•X)، باید درست باشد. با توجه به اینکه نتیجه شرطی U⊃(W•X) نادرست است، این شرطی تنها در صورتی درست است که مقدم آن، U، نادرست باشد. بنابراین یک F زیر U و یک T زیر نعل اسبی (رابط شرطی) U⊃(W•X) قرار می دهیم. و از آنجاکه U در مقدمه ۲ نادرست است، U را نیز در مقدمه ۱ نادرست میکنیم.

مقدمه ۲ اکنون درست است زیرا مقدم و نتیجه آن هر دو درست است.

با کار زدن دوباره راهبری IV، کنون ناچاریم یک گمارش مقدار ارزش در مقدمه ۱ انجام دهیم. با توجه به نادرستی U در مقدمه ۱، U∨V فقط وقتی درست است که V درست باشد.

مقدمه ۱ اکنون درست است، بنابراین ما یک T را زیر عملگر منطقی اصلی، نقطه (•)، در مقدمه ۱ قرار میدهیم.

مقدمه ۱ و ۲ اکنون درست هستند. اگر بتوانیم مقدمه ۳ را درست کنیم، استدلال نامعتبر میشود. از آنجایی که به V در مقدمه ۱ درست گمارده شده تا مقدمه ۱ درست باشد، باید در مقدمه ۳ نیز به V نیز درست بگماریم.

این موجب میشود که مقدمِ مقدمه ۳، یعنی T•V، درست باشد.

با توجه به اینکه W∨X درست است، تالی مقدمه ۳، ~(W∨X)، باید نادرست باشد.

مقدمه ۳، شرطی (T•V)⊃~(W∨X)، اکنون یک مقدم درست و یک تالی نادرست دارد که این موجب میشود مقدمه ۳ نادرست باشد.

اکنون سطر ۱ جدول ارزش کوتاهتر ما کامل است.
ما همیشه باید مراقب جداول ارزشِ کوتاه چند سطری باشیم تا نتیجه میانی صحیح را بدست آوریم. ما هنوز ثابت نکردیم که این استدلال معتبر است، زیرا هنوز نتیجه نادرست دوم را بررسی نکردهایم. آنچه تاکنون نشان دادهایم این است که وقتی W درست و X نادرست است، استدلال همه مقدمات درست و نتیجه نادرست ندارد. همانطور که میدانیم، ممکن است که استدلال بتواند همه مقدمات درست و یک نتیجه نادرست داشته باشد، مانند وقتی که W نادرست و X درست است. بنابراین اکنون باید دومین و آخرین نتیجه نادرست را بررسی کنیم.

ابتدا، W را نادرست و X را در هر جای دیگری که رخ دهد درست میکنیم. هر دو در مقدمه ۲ و در مقدمه ۳ رخ دادهاند.

باز هم، راهبری II، کارزدنی نیست زیرا هیچ مقدمهای نیست که گزاره هایساده یا نقیض گزارههای ساده باشند. بنابراین، راهبری IV، را کار میزنیم و با اجباری گمارش مقدار ارزش در سمت چپترین آغاز میکنیم. از آنجا که مقدمه ۱ فقط وقتی درست است که هر دو عطف آن درست باشد، T را درست ساخته و T را زیر گُوِه در َU∨V قرار میدهیم.

با توجه به اینکه T درست است، باید T را در مقدمه ۲ و در مقدمه ۳ درست کنیم.

مانند سطر ۱، اکنون دو گمارش اجباری مقدار ارزش، یکی در مقدمه ۲ و دیگری در مقدمه ۳ وجود دارد. با کارزدن راهبری IV، ما گمارش اجباری مقدار ارزش را در سمت چپترین انجام میدهیم. از آنجا که T به عنوان مقدمِ مقدمه ۲ درست است، نتیجه، U⊃(W•X)، باید درست باشد. با توجه به اینکه تالی شرطی U⊃(W•X) نادرست است، این شرطی تنها در صورتی درست است که مقدم آن، U، نادرست باشد. بنابراین یک F زیر U و یک T زیر نعل اسبی U⊃(W•X) قرار می دهیم.

مقدمه ۲ اکنون درست است زیرا مقدم و تالی آن هر دو درست هستند.

از آنجا که U در مقدمه ۲ نادرست است، U را باید در مقدمه ۱ نادرست ساخت.

با کارزدن دوباره راهبری IV، اکنون مجبوریم یک گمارش مقدار ارزش در مقدمه ۱ انجام دهیم. با توجه به نادرستی U در مقدمه ۱، َU∨V فقط وقتی درست است که V درست باشد.

مقدمه ۱ اکنون درست است، بنابراین ما یک T را زیر عملگر منطقی اصلی، نقطه (•)، مقدمه ۱ قرار میدهیم.

از آنجا که V در مقدمه ۱ درست شده است تا مقدمه ۱ درست باشد، باید درست را به V در مقدمه ۳ بگماریم.

این موجب میشود که مقدم ِ مقدمه ۳، T•V درست شود.

با توجه به اینکه W∨X درست است، تالی مقدمه ۳، ~(W∨X)، باید نادرست باشد.

مقدمه ۳، شرطی (T•V)⊃~(W∨X)، اکنون یک مقدم درست و یک تالی نادرست دارد که موجب میشود مقدمه 3 نادرست باشد.

سطر ۲ جدول ارزش کوتاهتر ما اکنون کامل شده است.
گام ۴: آزمون اعتبار.
اکنون ما سطر ۲ را تکمیل کردیم. در این روند تکمیل چه چیزی را نشان دادیم؟ تنها در سطر ۲، نشان دادهایم که وقتی W نادرست و X درست است، استدلال دارای همهیِ مقدمات درست و نتیجه نادرست نیست. اما این دومین ترکیب از تنها دو ترکیب مقادیر درست است که در آن نتیجه، W≡X، نادرست است، و در هر دو مورد، استدلال همهیِ مقدمات درست و نتیجهیِ نادرست را ندارد (یعنی نمیتواند داشته باشد).➥۱۷
۱۷- در مواردی مانند این، که در گمارشهای اجباری مقدار ارزش برای همه نتیجههای نادرست ممکن، همه مقدمات درست نیستند، این واقعیت که یک استدلال همه مقدمات درست را برای هر نتیجه نادرست ندارد، ثابت میکند که استدلال نمیتواند همه مقدمات درست را داشته باشد. برای هر نتیجه نادرست تنها چهار سطر در جدول ارزش ۳۲ سطری (خطوط ۱۲-۹) وجود دارد که در آنها مقدمه ۱ و مقدمه ۲ درست است (یعنی وقتی T درست است، U نادرست است و V درست است) و تنها در دو حالت از آنهادرست است. در این دو حالت (سطرهای ۱۰ و ۱۱) نتیجه نادرست است. جدول ارزش کوتاهتر ما این دو ترکیب مقدار ارزش را در جدول ارزش کامل (یعنی خطوط ۱۰ و ۱۱) نشان میدهد و بررسی میکند. نشان میدهد که تنها در دو حالتی که نتیجه نادرست است و مقدمات ۱ و ۲ درست است، مقدمه ۳ نادرست است. از آنجایی که این دو ترکیب مقادیر ارزش برای W و X تنها ترکیبهای مقدار ارزش هستند که نتیجه را نشان میدهند، W≡X، نادرست است، این ثابت میکند که استدلال نمیتواند همه مقدمات درست و یک نتیجه نادرست داشته باشد، که این ثابت میکند استدلال معتبر است..
■ حلاصه STTT
ما اکنون STTT را برای هفت استدلال مختلف به کار زدهایم. چهار استدلال اول را در جداول ارزش یک سطری آزمودیم زیرا نتیجه در آنها تنها از یک راه نادرست بود. در مثالهای ۵ و ۷، که نتیجه از چند راه نادرست است، تعیین کردیم که دنباله-C کارآمدتر است و سپس از گامهای ۳C، ۲C، و ۴ برای تعیین اعتبار استدلالها، به ترتیب در جداول سه سطری و دو سطری، استفاده کردیم. در مثال ۶، جایی که نتیجه از چند راه نادرست است، ما تعیین کردیم که دنباله-P کارآمدتر است، و بنابراین از گامهای ۳P، ۲P، و ۴ برای اثبات کارآمد اعتبار استدلال در یک سطر استفاده کردیم.
گام ۱: تعیین کنید که آیا هر مقدمه به راههای کمتر نسبت به نادرست بودن نتیجه درست است یا خیر.
گام ۲: با (C) نتیجه را نادرست کنید یا با (P) همهیِ مقدمات را درست کنید.
گام ۳: با (C) تا جایی که ممکن است مقرمات را درست سازید یا (P) نتیجه را نادرست کنید.
گام ۴: آزمون برای اعتبار را اجرا کنید.
راهبری I: در صورت امکان، ابتدا گمارش اجباری مقادیر ارزش را برای نتیجه یا یک مقدمه انجام دهید، همانطور که در گام ۱ از STTT چهار (۴) مرحلهای تعیین شده است (به بند (B) مراجعه کنید).
راهبری II: قبل از گمارش مقدار ارزش اجباری به مقدماتی که گزاره های ساده یا نقیض گزارههای ساده هستند، گمارش اجباری مقدار ارزش به مقدمههای ترکیبیتر را انجام دهید.
راهبری III: اگر گمارش مقدار ارزش اجباری وجود ندارد یا دیگر وجود ندارد، گمارشهای مقدار ارزش غیراجباری را به نتیجه انجام دهید تا از هر راه ممکن نادرست شود، یا گمارشهای مقدار ارزش غیراجباری را در کمترین راهها به مقدمات انجام دهید که در کمترین تعداد راه ممکن درست است.
راهبری IV: اگر گمارش مقدار ارزش به دو یا چند مقدمه به طور معادل (مثلاً به دو گزاره ساده) اجباری است یا به همان اندازه غیراجباری است، ابتدا گمارش مقدار ارزش در سمت چپترین را انجام دهید.
راهبری V: در ساخت یک جدول ارزش کوتاه چند سطری، یک نتیجه نادرست (یا یک مقدمه درست) بسازید
(الف) فقط با استفاده از آن دسته از ترکیبات مقادیر ارزش که مقدار ارزش دلخواه را برای آن گزاره مرکب بهدست میدهند، و
(ب) اینها را به ترتیبی مرتب کنید در یک جدول ارزش تمامشده پدیدار میشوند (به بخش ۹.۶ - آزمون اعتبار با جدول ارزش - مراجعه کنید). برای مثال، برای یک گزاره مرکب متشکل از دو گزاره ساده، به ترتیب، فقط از ترکیباتی که TT، TF، و FT و FF استفاده کنید که مقدار ارزش مورد نظر را برای عبارت-گزارهای بهدست میدهند.
بیاعتباری: ما بیاعتباری یک استدلال را با ساختن یک سطر جدول ارزش برای یک ترکیب از مقادیر ارزش برای گزارههای ساده تشکیل دهنده که در آن مقدمات همه درست و نتیجه نادرست است، ثابت میکنیم.
اعتبار: ما اعتبار یک استدلال را با اثبات اینکه مقدمات نمیتوانند برای هر نتیجه نادرست (یعنی دنباله-C در STTT) درست باشند، یا با اثبات اینکه نتیجه نمیتواند برای هر مجموعهای از مقدمات درست نادرست باشد (یعنی دنباله-P در STTT) اثبات میکنیم.
مطالب تکمیلی در مورد STTT در ضمیمه های B، A و C در پشت این کتاب ارائه شده است.
تمرین
برای هر یک از استدلالهای زیر، از STTT برای تعیین اعتبار یا بیاعتبارین استدلال استفاده کنید. برای برخی از این استدلال ها، گامهای ۳C ،۲C، و ۴ (یعنی دنباله-C) کارآمدترین خواهند بود. برای برخی از این آرگومان ها، گامهای ۳P ،۲P، و ۴ (یعنی دنباله-P) بسیار کارآمد خواهند بود. (پاسخ تمرینهای ستارهدار بعد از صورت تمرینها آمده است.)
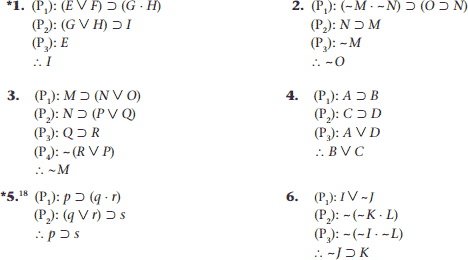
اگر در تمرین ۵ متغیرهای گزارهای p، q، r و s را به ترتیب با گزارههای ساده T, U, V و W جایگزین کنیم، استدلال زیر به دست میآید.
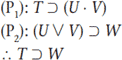
[۱۸]- این مثال با استفاده از (Complete Truth-Table Method / CTTM) در فصل ۹ قسمت ۶ ( آزمون اعتبار استدلال بر پایه جدول ارزش) آزمون شده است.
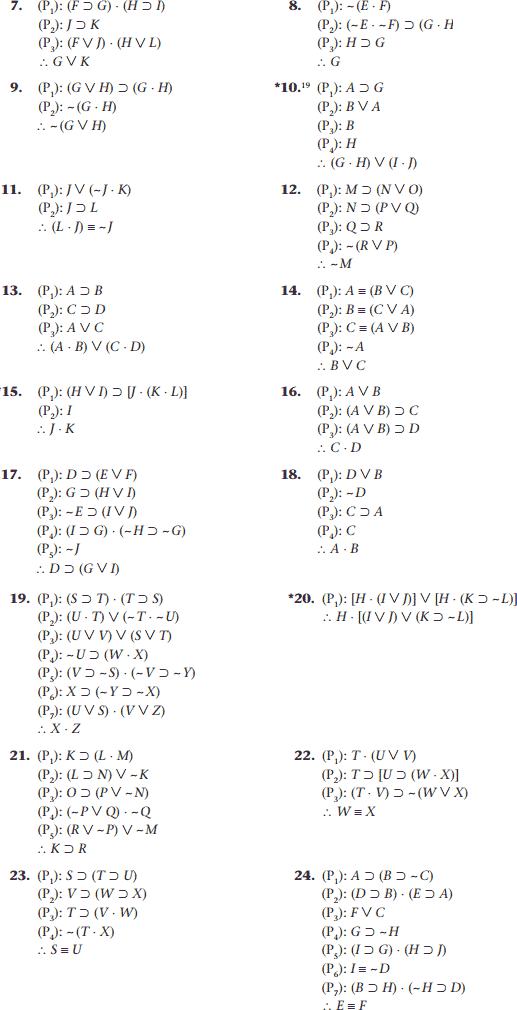
پاسخ تمرینهای ستارهدار
۱-
نتیجه این استدلال گزاره ساده I است، بنابراین با مرحله ۲C شروع می کنیم.
نتیجه، یعنی I، نادرست است. مقدمه ۳، یعنی E، درست است. از آنجا که E درست است، E∨F نیز درست است، به این معنی که مقدمه ۱ تنها در صورتی درست است که G•Hدرست باشد؛ و این وامیدارد که G درست باشد و نیز H درست باشد. که این به نوبه خود، G∨H را درست میسازد، و این با توجه به نادرستی I، مقدمه ۲ را نادرست میکند . پس استدلال معتبر است.

۵-
این مثال در مقدمه این قسمت (۱۰.۹) آمده است و با استفاده از CTTM (جدول ارزش کامل) در قسمت ۹.۶ از فصل ۹ به آزمون درآمده است.
(P۱): p ⊃ (q • r)
(P۲): (q ∨ r) ⊃ s
∴ p ⊃ s
اگر متغیرهای گزارهای p، q، r و s را به ترتیب با گزارههای ساده T، U، V و W در صورت استدلال بالا جایگزین کنیم، زیر به دست میآید.
(P۱): T ⊃ (U • V)
(P۲): (U ∨ V) ⊃ W
∴ T ⊃ W
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
نتیجه T⊃W شرطی است که تنها از یک راه، وفتی که T درست و W نادرست است، نادرست است. از آنجا که هیچ مقدمهای نمیتواند به راههای کمتری درست باشد، ما با گامهای ۳C، ۲C ، و ۴ را ادامه میدهیم.
گام ۲C: نتیجه را نادرست سازید.
نتیجه، یعنی شرطی T⊃W است، بنابراین ما با قرار دادن یک F زیر نعل اسبی در T⊃W آغاز میکنیم.

نتیجه، یعنی T⊃W، تنها از یک راه میتواند نادرست باشد: مقدم آن T درست باشد و W تالی آن نادرست باشد. بنابراین، ما باید این گمارش اجباری مقادیر ارزش را به T و W در نتیجه انجام دهیم.

به محض اینکه در نتیجه T را درست و W را نادرست کنیم، باید همان گمارش مقدار ارزش را بطور سازگار به T و W در هر جای دیگری که رخ دهند، انجام دهیم. T در مقدمه ۱ و W در مقدمه ۲ رخ میدهد.

گام ۳C: تا جایی که ممکن است مقدمات را درست بسازید.
به پیروی از راهبری I، میپرسیم آیا گمارش مقدار ارزش اجباری دیگری وجود دارد؟
پاسخ آری است. دو گمارش اجباری مقدار ارزش وجود دارد: (۱) با توجه به اینکه تالی مقدمه ۲ نادرست است، مقدمه ۲ تنها وقتی میتواند درست باشد که مقدم آن نادرست باشد. و (۲) با توجه به اینکه مقدمِ مقدمه ۱ درست است، مقدمه ۱ تنها در صورتی میتواند درست باشد که تالی آن درست باشد. با توجه به اینکه اینها به یک اندازه گمارشهای مقدار ارزش اجباری هستند، ما راهبری III، را پی میگیریم و سمت چپترین گمارش مقدار ارزش اجباری را به U•V اعمال میکنیم.

اگر ترکیب عطفی U•V در مقدمه ۱ درست باشد، هم U و هم V باید درست باشند، بنابراین آنها را در مقدمه ۱ درست میسازیم.

مانند همیشه، باید همان مقدار ارزش را به U و V در هر جای دیگری که رخ دهند بگماریم، که هر دو در مقدمه ۲ رخ میدهند.

این گمارش مقدار ارزش به U و V در مقدمه ۲ موجب میشود که فصلی U∨V در مقدمه ۲ درست باشد.

و اگر U∨V درست و W نادرست باشد، مقدمه ۲ نادرست است.

گام ۴: آزمون اعتبار.
در گمارش اجباری مقدار ارزش به T و W در نتیجه استدلال، سپس به U و V در مقدمه ۱ و سپس به U و V در مقدمه ۲، میتوانیم نتیجه را نادرست و مقدمه ۱ را درست کنیم، اما مقدمه ۲ نادرست است. با توجه به اینکه اینها تنها گمارشهای مقدار ارزش هستند که نتیجه با آنها نادرست است و نیز مقدمه ۱ درست است، ما ثابت کردهایم که استدلال نمیتواند همه مقدمات درست و یک نتیجه نادرست داشته باشد، و این ثابت میکند استدلال معتبر است.
۱۰-
STTT برای نتیجهای که در گمارشهای متعدد مقدار-ارزش نادرست است را برای این استدلال (تمرین ۱۰) را با استدلال آمده در پیوست A مقایسه کنید.
همانند استدلال مشابه در پیوست A، این استدلال به یک جدول ارزش کامل ۶۴ سطری نیاز دارد. و اگر گام ۲C را به اشتباه به کار ببندیم و ابتدا نتیجه را نادرست کنیم، STTT در صورت معتبر بودن استدلال به ۹ سطر نیاز دارد. با این حال، بر خلاف استدلال پیوست A، ما نمیتوانیم به آسانی راهی برای اثبات اعتبار این استدلال بیابیم.
گام ۱: تعیین کنید آیا مقدمهای به تعداد راه کمتر از نتیجه نادرست است.
همانند استدلال پیوست A، ابتدا تعیین میکنیم که مقدمه ۳ (یعنی B) و مقدمه ۴ (یعنی H) هر کدام تنها برای یک ترکیب از مقادیر ارزش برای گزاره(های) ساده تشکیل دهنده خود درست هستند، و بنابراین، در ادامه مرحله ۲P و راهبری II و III، ابتدا یک گمارش اجباری مقدار ارزش به گزاره ساده B و سپس به گزاره ساده H انجام میدهیم.
گام ۲P: همه مقدمات را درست سازید.

در این حالت، ما خود انتخاب کردهایم که ابتدا همه مقدمات را درست سازیم، زیرا میدانیم که دو گمارش مقدار ارزش اجباری برای گزارههای ساده در مقدمات وجود دارد: مقدمه ۳ فقط در صورتی درست است که B درست باشد و مقدمه ۴ فقط درست است.اگر H درست باشد.

از آنجا که B در مقدمه ۳ درست است، باید B را در مقدمه ۲ درست کنیم.

درستی B در مقدمه ۲، فصلی B∨A را درست میسازد.

از آنجا که H در مقدمه ۴ درست است، باید H را در نتیجه درست کنیم.

در این ترکیب فصلی، میپرسیم آیا گمارش مقدار ارزش اجباری دیگری وجود دارد؟ پاسخ خیر است. به همین دلیل، ما ابتدا سمت چپترین گمارش مقدار ارزش را انجام میدهیم و مقدمه ۱، یعنی A⊃G، را درست میسازیم. از آنجا که سه راه برای درستی A⊃G وجود دارد (T. T، F. T و F. F) راهبری IV را اعمال می کنیم و ابتدا A را درست و G را درست میکنیم.

این هر چهار مقدمه را درست میکند، اما درستی G موجب میشود G•H درست باشد که نتیجه را درست میکند.

بنابراین، ما باید یک سطر دوم ایجاد کنیم و با اعمال دوباره راهبری IV، مقدمه ۱ را به راه دوم درست کنیم، یعنی با نادرست کردن A و درست کردن G.

اکنون هر چهار مقدمه درست است. از آنجاکه، G در مقدمه ۱ درست است، G باید در نتیجه درست باشد، و این G•H و نیز نتیجه، یعنی (G•H)∨(I•G)، را درست میکند.

باز هم، ما نتوانستیم همه مقدمات را درست و نتیجه را نادرست کنیم. آیا این ثابت میکند که استدلال معتبر است؟ خیر، زیرا ما هنوز همه ترکیبهای مقادیر-ارزش، که همه مقدمات را درست میکند، را بررسی نکردهایم. ما باید یک بار دیگر راهبری IV را برای مقدمه ۱ اعمال کنیم و آخرین ترکیب مقدار ارزش را امتحان کنیم که در آن مقدمه ۱ درست است: یعنی A نادرست است و G نادرست است.

از آنجا که G در مقدمه ۱ نادرست است، G باید در نتیجه نادرست باشد، تا G•H را نادرست کند.

گام ۳P: نتیجه را نادرست سازید.
ما اکنون موفق شدهایم همه مقدمات را درست و فصلی در یال چپ نتیجه را نادرست کنیم! اگر بتوانیم فصلی سمت راست نتیجه را نادرست کنیم، آنگاه ثابت خواهیم کرد که استدلال نامعتبر است.
البته سه راه برای ایجاد فصلی سمت چپ نتیجه، I•J، وجود دارد تا آن را نادرست کرد، و با توجه به اینکه نه I و نه J در جای دیگری از استدلال رخ نمیدهند، طبق راهبری IV پیش میرویم و اولین گمارش مقدار ارزش را انجام میدهیم که I•J را نادرست، یعنی T•F، میسازد.

اکنون و سرانجام، با توجه به اینکه هر دو فصل، G•H و I•J، نادرست هستند، نتیجه، (G•H)∨(I•G)، نادرست است.

گام ۴P: آزمون اعتبار.
کار به پایان رسیده. ما گمارشهای اجباری مقدار ارزش را به B و H انجام دادیم، و سپس برای درست کردن مقدمه ۲، راهبری IV را پی گرفتیم و در سومین تلاش، هر چهار مقدمه را درست و فصلی چپ نتیجه را نادرست کردیم. نادرست ساختن فصلی سمت راست نتیجه و در پی آن نادرست ساختن نتیجه کار آسانی بود. جدول ارزش کوتاهتر سه سطری ما اکنون دارای تمام مقدمات درست و یک نتیجه نادرست است که این ثابت میکند این استدلال نامعتبر است.
درست ساختن تمام مقدمات در این استدلال، STTT بسیار کارآمدتر از CTTM با ۶۴ سطر است و بسیار کارآمدتر از نادرست ساختن نتیجه در ابتدا (گام ۲C) است، که ممکن است نیاز به یک جدول ارزش کوتاهتر ۹ سطری نیازمند باشد (گرچه بیاعتباری این استدلال در سطر ۲ آشکار میگردد).
۱۵-
نتیجه یک عطفی است که از به سه راه نادرست است. مقدمه ۲ گزاره ساده I است که از یک راه درست است. بنابراین، ما گام ۲P را دنبال میکنیم: درستی I وامیدارد که J، K و L در مقدمه ۱ درست باشند، که این خود وامیدارد نتیجه درست باشد.

این ثابت میکند که استدلال نامعتبر است.
۲۰-
نتیجه یک عطفی مرکب از یک گزاره ساده و یک یک فصلی پیچیده است.
نتیجه از سه راه نادرست است: T•F، F•T و F•F.
مقدمه از سه راه درست است: T∨T، T∨F و F∨T. در هر یک از این سه را، H باید درست باشد. اما عطفی سمت چپ هر فصل میتواند از چند راه نادرست باشد. بنابراین ما گام ۲C را به کار میزنیم.

