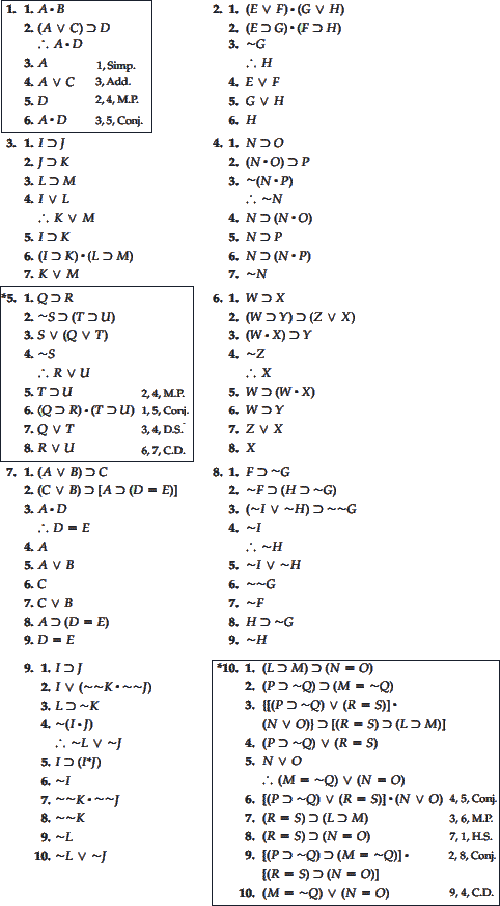نمایانسازی برهان صوری اعتبار
روشهای استنتاج
درآمد به منطق فصل ۱۰ قسمت ۳
در فصل پیشین توضیح ۹ صورت استدلال معتبر ابتدایی بعنوان ۹ قاعده استنتاج را به قرار: ۱- قیاس استثنایی ۲- قیاس اقترانی ۳- قیاس شرطی ۴- قیاس فصلی ۵- دو لِمّی ساختی ۶- جذب ۷- ساده گردانی ۸- پیوست ۹- افزایش دیدیم. قواعد استنتاج پیوند دهنده اجزای استدلال هستند و برای چیرگی در ساختن برهان باید در آغاز به تمامی با شکل و ضرب آهنگ آنها آشنا شد. این قسمت به نمایان سازی چنین روندی میپردازد.
۳.۱۰ نمایانسازی برهان صوری اعتبار
ما، برهان صوری اعتبار یک استدلال داده شده را همچون دنبالهای از عبارتهای-گزارهای بهگونهای تعریف کردیم که هر یک از این عبارتهای گزارهای خود:
آ- یک مقدمه آن استدلال باشد یا
ب- از عبارتهای گزارهای قبلی دنباله بطور معتبر دست آمده باشد،
آنگونه که آخرین عبارت گزارهای این دنباله، نتیجه استدلال مورد اثبات باشد.
بنابراین باید برای اثبات اعتبار استدلالهایی که با آن مواجه میشویم چنین دنبالههایی را بسازیم.
انجام این کار میتواند چالش برانگیز باشد. بنابراین بهتر است قبل از تلاش برای ساختن چنین دنبالههایی، بکوشیم تا با ظاهر و ویژگیهای برهانهای صوری آشنا شویم. در این قسمت تعدادی برهان صوری کامل را بررسی میکنیم تا ببینیم آنها چگونه کار میکنند و نیز "درک و حس" از آنها را برای ساختنشان بدست آوریم.
قدم اول ما ساختن فوری چنین برهانهایی نیست، بلکه ابتدا کوشش به فهم و ارزشمندی آنها خواهیم کرد. در هر حالت دنبالهای از عبارتهای گزارهای در مقابل ما قرار داده خواهد شد. هر عبارت-گزارهای در این دنباله یک مقدمه است یا از عبارتهای-گزارهای قبلی و یکی از صورتهای استدلال معتبر مقدماتی بدست آمده _ درست مانند مثال آمده در قسمت ۱۰.۱. وقتی ما با چنین برهانی، البته بدون اشاره به قاعده استنتاج که هر مرحله را موجه میسازد، روبرو میشویم، متوجه هستیم (ازآنجاکه به ما گفتهشده این برهان کامل است) هر خط در برهان که خود یک مقدمه نیست باید از خطوط قبلی نتیجهشده باشد. برای فهم این نتیجه شدنها میباید نه استدلال معتبر مقدماتی در ذهن آماده باشند.
اکنون بجاست تا به بعضی برهان که این استواری ستودنی را به نمایش میگذارند نگاهی انداخته. اولین مثال تمرین یکم از مجموعه تمرینی است که در پایان این قسمت آمده.
مثال ۱
۱. A • B
۲. (A ∨ C) ⊃ D
∴ A • D
۳. A
۴. A ∨ C
۵. D
۶. A • D
همانطور که میتوان دید دو خط اول برهان مقدمه هستند، زیرا قبل از نماد "بنابراین"، یعنی ∴، ظاهرشدهاند؛ آنچه بلافاصله در سمت راست این نماد آمده، یعنی A•D، نتیجه این مقدمه است. آخرین خط دنباله نیز همان نتیجه است (چراکه اگر برهان صوری صحیح باشد باید اینگونه هم باشد). چه میتوان درباره گامهای بین مقدمات و نتیجه گفت؟ خط ۳ یعنی A را میتوانیم از خط ۱ یعنی A•B بوسیله ساده گردانی استنتاج کنیم. بنابراین در سمت راست خط ۳ شمار خط و قاعدهای که این خط از آن نتیجه شده یعنی "۱,Simp." را مینویسیم. خط ۴ عبارت گزارهای A∨C است. چگونه این خط از خطهای بالاتر آن استنتاج شده؟ نمیتوان آن را از خط ۲ بوسیله سادهگردانی نتیجه بگیریم. اما میتوان آن را از خط ۴ بوسیله افزایش استنتاج کرد. افزایش به ما میگوید اگر p درست باشد آنگاه p∨q، هرچه q باشد، درست است. با کاربرد دقیق این الگوی منطقی میتوانیم از اینکه A برقرار است نتیجه گرفت A∨C درست است. بنابراین در سمت راست خط ۴ عبارت "۳, Add."را قرار میدهیم. خط ۵ همان D است. D در خط ۲ بهعنوان تالی یک عبارت-گزارهای شرطی، A∨C)⊃D)، ظاهرشده. ما در خط ۴ ثابت کردیم که A∨C درست است؛ اکنون با کار زدن قیاس استثنائی این را با شرطی خط ۲ ترکیب میکنیم تا D را ثابت کنیم. بنابراین سمت راست خط ۵ عبارت "۲, ۴, M.P." را قرار میدهیم. اکنون ثابت شد که D درست است (در خط ۳) و نیز ثابت شد که A درست است (در خط ۵). پس میتوانیم آنها را بهطور معتبر باهم پیوست کنیم، و این همان A•D است که در خط ۶ تصدیق شده. بنابراین در سمت راست خط ۶ عبارت "۵, ۳, Conj." را قرار میدهیم. این خط، A•D، نتیجه استدلال است و بنابراین این خط آخرین عبارت-گزارهای در دنباله عبارتهای-گزارهای است که این برهان را تشکیل میدهند. اکنونکه این برهان ارائه شده به ما کامل است میتوان آن را بوسیله مشخص کردن توجیه هر مرحله در آن "فربه" نیز کرد.
در این مثال و تمرینانی که خواهد آمد، هر خط هر برهان میتواند بوسیله یک صورت استدلال معتبر مقدماتی توجیه شود. هیچ استنتاج دیگری از هیچ نوع گرچه به نظر مقدماتی هم بیاید مجاز نیست. وقتی در وضعی هستیم که میخواهیم به یک صورت استدلال که دارای دو مقدمه است رجوع کنیم (مانند M.P. یا D.S.) در قسمت توجیه ابتدا شماره خطهای بکار بسته را به ترتیبی که در صورت معتبر مقدماتی ظاهرشدهاند میآوریم. ازاینجهت است که خط ۵ مثال ۱ با "۲, ۴, .M.P" دارای توجیه گردیده.
برای چیره شدن در ساختن برهانهای صوری باید کاملاً با شکل و ضرب آهنگ نُه صورت استدلال مقدماتی آشنا شویم— نُهگانه اول از قواعد استنتاج که بسیار زیاد آنها را بکار خواهیم زد.
تمرین
هریک از تمرینات زیر یک برهان صوری بیعیب و نقص را برای استدلال اشارهشده نشان میدهد. برای هرکدام از خطهای شمارهدار که مقدمه نیست توجیه آن را قرار دهید.