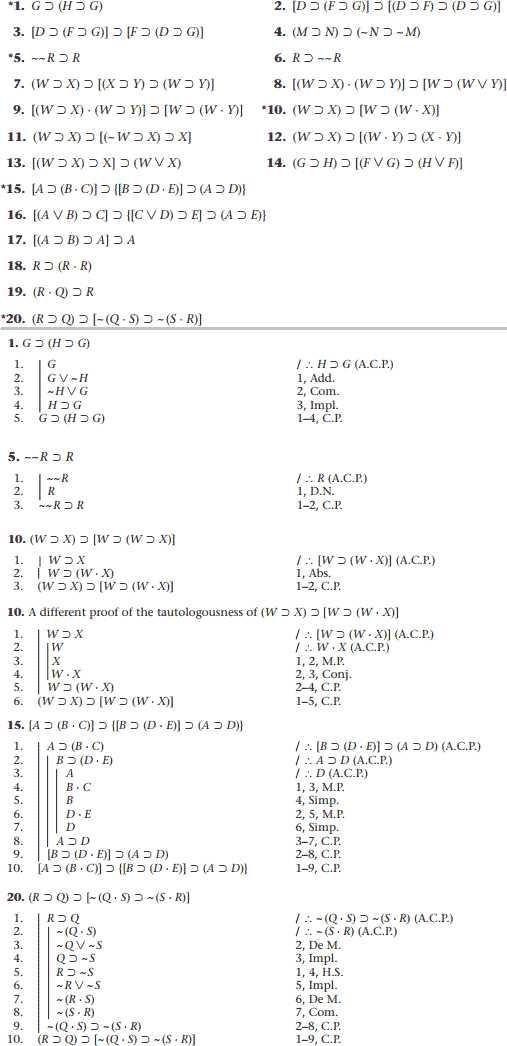
برهان شرطی
روشهای استنتاج
درآمد به منطق فصل ۱۰ قسمت ۱۰۱
در قسمت پیشین، به ناسازگاری در منطق پرداختیم و توضیح دادیم، هر صورت استدلال با مقدمات ناسازگار معتبر است ولی استوار نیست؛ نیز از هر مجموعه مقدمات ناسازگار هر نتیجهای دست آمدنی است. موضوع این قسمت روش (قاعده) برهان شرطی در برهان آوری برای استدلال است. کارزدن این روش بهعنوان یک قاعده استنتاج، افزون بر نوزده قاعده استنتاج، برهان آوری را هم ساده و هم کوتاه میکند. کارزدن این قاعده در زبان (دانسته، ندانسته و بجا، نابجا) بسیار رایج است. بنابراین، این قسمت موشکافی این قاعده است.
۱۰۱.۱۰ برهان شرطی
برهان شرطی
Conditional Proof
برهانی که در آن، گزارهای مانند p فرض گرفته میشود، سپس با کارزدن تعداد محدود قواعد استنتاج، برخی گزاره مانند q استنتاج میشود، و در پایان، از طریق قاعده «برهان شرطی (.C.P)»، گزاره اثباتشده «p⊃q» (یعنی، اگر p آنگاه q) اندریافت میشود.
نوزده قاعده استنتاج (همانطور که در ۱۰.۷ دیدیم) تمام هستند. یعنی، برای هر استدلالِ تابع-ارزشِ معتبر، میتوان فقط با استفاده از این نوزده قاعده برهان آورد. با این حال، برخی برهانها طولانی و دشوارند. در این قسمت، قاعده جدیدی، به نامِ قاعده برهان شرطی (C.P.)، را معرفی میکنیم که بسیاری از برهانها را کوتاه و ساده میکند. این قاعده دارای پیکربندی چندان سادهای نیست و از همین جهت با بقیه متفاوت است. قاعده برهان شرطی در واقع یک تکنیک است و توسط آن میتوان یک گزاره شرطی را با فرض گرفتن فرضیِ مقدم آن و استنتاج تالی آن از آن فرضِ فرضی اثبات کرد. صورت استدلال فرضیِ یک برهان شرطی به قرار زیر است:
p ... ... ... q | /∴ q (C.P. فرض) |
| p ⊃ q |
همانطور که خواهیم دید، گزاره q را در تعداد محدود از مراحل از گزاره فرض گرفتهیِ p (و معمولاً نیز، از مقدمات و/یا گزارههای دست آمده) استنتاج میکنیم و سپس p⊃q را نتیجه میگیریم. از قاعده برهان شرطی (C.P.) میتوان برای استنتاج معتبر هر گزاره که از مقدمات به دست میآید بهره برد و تنها به دستآوردن یک نتیجه شرطی محدود نمیشود. در واقع، همانطور که در ادامه (ه) خواهیم دید، میتوان با استفاده از C.P. و بدون هیچ مقدمه ثابت کرد که آیا یک عبارت گزارهای یک توتولوژی است یا نه.
آ. توضیح و موجه کردن برهان شرطی
برهان شرطی (C.P.) را میتوان با ارجاع به اصل واگردان و تناظر (آمده در قسمت ۹.۸ - د) بین صورت استدلالی معتبر و توتولوژی به بهترین وجه توضیح داد و آن را موجه کرد.
هر استدلال معتبر با یک گزاره شرطی توتولوژیک مطابقت دارد که مقدم آن، ترکیب عطفی مقدماتِ استدلال است و تالی آن، نتیجه آن استدلال است. فرض کنید استدلالی پیش روی ما است که دارای یک نتیجه شرطی با نماد A⊃C است. همچنین فرض کنید که عطف مقدمات آن را با P➥۲۲ نشان دهیم. این استدلال را I مینامیم.
(P۱): P
∴ A ⊃ C استدلال I
استدلال I معتبر است اگر و تنها اگر گزاره شرطی متناظر آن
P ⊃ ( A ⊃ C) (۱)
یک توتولوژی باشد. اگر بتوانیم نتیجه A⊃C را از مقدمات عطف شده در P بوسیله دنبالهای متناهی از گزارههای و با استفاده از نوزده قاعده استنتاج بهدست آوریم، آنگاه ثابت کردهایم که استدلال I معتبر است و شرطی مرتبط با آن (۱) یک توتولوژی است. اکنون میگوییم (۱) بوسیله واگردان منطقاً همارز (۲) است.
(P • A) ⊃ C (۲)
و (۲) یک شرطی است که با استدلالی تا اندازهای متفاوت، یعنی استدلال II، مرتبط است.
(P۱): P
(P۲): A
∴ Cاستدلال II
این استدلال دوم، به عنوان مقدمات خود، همهیِ مقدمات استدلال I به اضافه یک مقدمه اضافی، یعنی عبارت-گزارهای A، را دارد، که تالیِ نتیجهیِ استدلال I است. و نتیجه استدلال II تالیِ نتیجه استدلال I است. اگر نتیجه استدلال II، یعنی عبارت-گزارهای C، را از مقدمات عطفشده در P•A با دنبالهای از گزارههای بهدستآمده با استفاده از قواعد نوزده گانه نتیجه بگیریم، بدین ترتیب ثابت میکنیم که گزاره شرطی مرتبط با آن (۲) یک توتولوژی است. اما از آنجایی که (۲) و (۱) همارز منطقی هستند، برای اثبات اینکه (۲) یک توتولوژی است، ثابت کردیم که (۱) یک توتولوژی است، که از آن، استدلال اصلی، استدلال I - با یک مقدمه کمتر نتیجه میشود و از این، نتیجه شرطی، یعنی A⊃C، نیز معتبر است.
بطور کلی، برای هر مجموعهای از مقدماتِ P، و برای هر عبارت-گزارهای A و C، استدلال I معتبر است، اگر و تنها اگر استدلال II معتبر باشد. بنابراین، میتوان اعتبار استدلال I
(P۱): P
∴ A ⊃ C استدلال I
را با افزودن A به مقدمات P در استدلال I اثبات کرد و سپس C را بوسیله دنبالهای متناهی از گزارهها که با کارزدن نوزده قاعده استنتاج بهدست آورد. به این ترتیب، اعتبار استدلال دوم
(P۱): P
(P۲): A
∴ Cاستدلال II
را اثبات میکنیم.
این دلیلآوری «برهان شرطی (C.P.)» را به تمامی موجه میکند.
ب. روند برهان شرطی
اکنون روند کلی برای برهان شرطی را نشان میدهیم. استدلال زیر را در نظر بگیرید.
(P۱): (A ∨ B) ⊃ (C • D)
(P۲): (D ∨ E) ⊃ F
∴ A ⊃ F
برای اثبات اعتبار این استدلال با استفاده از C.P.، ابتدا، طبق معمول، دو مقدمهِ استدلال را در سطرهای ۱ و ۲ نوشته، سپس نتیجه آن را در ستون توجیهی در سطر ۲، مقدمشده با یک کجخط و نماد نتیجه (یعنی، /∴)، مینویسیم.
۱. (A ∨ B) ⊃ (C • D)
۲. (D ∨ E) ⊃ F /∴ A ⊃ F
از آنجا که نتیجه یک گزاره شرطی است، برهان شرطی را با فرضِ مقدمِ گزاره شرطی A⊃F، یعنی A آغاز میکنیم. با قرار دادن یک خط عمودی، به نام خط قلمرو در سمت چپ، نشان میدهیم که گزاره A یک فرض است.
۱. (A ∨ B) ⊃ (C • D)
۲. (D ∨ E) ⊃ F /∴ A ⊃ F
۳. A /∴ F (C.P فرض)
در ستون توجیهی، "/∴" را مینویسیم، در پی آن نتیجه مورد نظر برای زیر-برهان C.P.، یعنی F، و به دنبال آن "(فرض، C.P.)" را مینویسیم تا نشان دهیم که گزاره A فرضِ برهان شرطی است. هر گزاره که با استفاده از این فرض استنتاج شود در قلمرو آن خواهد بود، بنابراین خط قلمرو عمودی به سمت پایین گسترش مییابد تا این را نشان دهد.
اثبات استدلال فوق فقط با استفاده از نوزده قاعده استنتاج نیاز به ۲۰ سطر است، حال آنکه، برهانِ شرطی برای آن بس کوتاهتر و سادهتر است.
| ۱. | (A ∨ B) ⊃ (C • D) | |
| ۲. | (D ∨ E) ⊃ F | /∴ A ⊃ F |
| ۳. | A | /∴ F (C.P فرض) |
| ۴. | A ∨ B | ۳, Add. |
| ۵. | C • D | ۱, ۴, M.P. |
| ۶. | D • C | ۵, Com. |
| ۷. | D | ۶, Simp. |
| ۸. | D ∨ E | ۷, Add. |
| ۹. | A | ۲, ۸, M.P. |
| ۱۰. | A ⊃ F | ۳ - ۹, C.P. |
وقتی گزارهای که باید در برهان شرطی نتیجه شود، یعنی F در سطر ۹ بهدست آمد، این فرض را تخلیه میکنیم و خط قلمرو را برای برهان شرطی پایان میدهیم، که این نشان میدهد ما برهان شرطییِ F را از دو مقدمه و فرض اضافی، یعنی عبارتِ-گزارهای A، به پایان رساندهایم. این برهان شرطی ثابت می کند که گزاره شرطی A⊃F به تنهایی از این دو مقدمه بطور معتبر نتیجه میشود. برای نشان دادن آشکار این موضوع، عبارت A⊃F را بلافاصله زیر خط قلمرو برهان شرطی مینویسیم. در ستون توجیهی، محدوه قلمرو سطرها را در برهان شرطی نشان میدهیم، یعنی (سطرهای) "۹-۳"، و "C.P." را نوشته تا نشان دهیم این سطر A⊃F با استفاده از برهان شرطی استنتاج شده است.
این برهان شرطی ثابت میکند که اگر علاوه بر دو مقدمه درست، گزاره A نیز درست باشد، F نیز درست است، یعنی، اگر دو مقدمه درست باشند A⊃F (اگر A آنگاه F) باید درست باشد. به عبارت دیگر، A⊃F بطور معتبر به وسیله یک برهان شرطی، تنها از دو مقدمه اندریافت میشود. اکنون، اعتبار این استدلال با استفاده از چهار قاعده استنتاج و برهان شرطی (C.P.) به اثبات رسیده است.
هرگز نباید از یاد برد، فرضی که برای برهان شرطی معرفی میشود قلمرو محدودی دارد. خط عمودی برای یادآوری همین موضوع است. اندریافتهای انجام شده در قلمرو آن فرض، در تمام درازنای برهان شرطی (C.P.)، محدود به زیر-برهان شرطی C.P. است و نمیتواند بیرون از قلمرو برهان شروطی (یعنی پس از تکمیل برهان شرطی استفاده شود). برای مثال، در سطر ۶، عبارت D•C از دو فرض و فرض اضافی C.P. ("بطور موقت")، یعنی عبارت-گزارهای A استنتاج میشود. ترکیب عطفی D•C تنها از دو مقدمه بهدست نمیآید. بلکه، از ترکیب دو مقدمه و فرض C.P.، عبارت-گزارهای A، نتیجه میشود. از آنجایی که قلمرو فرض برهان شرطی و خود زِبَر-برهان شرطی با خط قلمرو عمودی نشان داده میشود، آن خط دامنه وقتی پایان مییابد که این فرض تخلیه شود و برهان شرطی پایان رسیده باشد. پس از آن، نتیجه برهان شرطی زیر-برهان شرطی، خارج از برهان شرطی و خط قلمرو آن نوشته میشود.
به همین دلیل، گزارههای نتیجهشدهیِ درون یک برهان شرطی - درون قلمرو فرض آن (یعنی در محدوده خط قلمرو آن) - نمیتوانند بیرون از (پس از) برهان شرطی استفاده شوند، زیرا چنین گزارههای استنتاجی لزوماً از مقدمات به تنهایی بهدست نمیآیند. برای نمونه، D∨E که در سطر ۸ بهدست میآید، نمیتواند با مقدمه ۲ برای استنتاج F در سطر ۱۱ توسط قیاس استثنایی استفاده شود.
| ۱. | (A ∨ B) ⊃ (C • D) | |
| ۲. | (D ∨ E) ⊃ F | /∴ A ⊃ F |
| ۳. | A | /∴ F (C.P فرض) |
| ۴. | A ∨ B | ۳, Add. |
| ۵. | C • D | ۱, ۴, M.P. |
| ۶. | D • C | ۵, Com. |
| ۷. | D | ۶, Simp. |
| ۸. | D ∨ E | ۷, Add. |
| ۹. | A | ۲, ۸, M.P. |
| ۱۰. | A ⊃ F | ۳ - ۹, C.P. |
| ۱۱. | F خطا | ۲, ۸, M.P. |
استنتاج F در سطر ۱۱ نادرست است زیرا بخشی از استنتاج آن از D∨E است که در دامنه خط قلمرو (و گزاره فرض شده A) قرار دارد. D∨E تنها از مقدمات استنتاج نشده است. در واقع، D∨E صرفاً از مقدمات بطور معتبر بهدست نمیآید. چرا که D∨E به ضرورت و تنها از مقدمات نتیجه نشده و نمیتوان آن را در استنتاجهای خارج از قلمرو (یعنی بعد از) برهان شرطی و فرض آن بهکار برد. هیچ عبارت-گزارهای که در سمت راست خط قلمرو قرار میگیرد را نمیتوان پس از پایان خط قلمرو (یعنی پس از تخلیه فرض) در استنتاج بهکار برد. ولی، میتوان از گزارههایی استفاده کرد که قبل و بعد از برهان شرطی (یعنی زیر انتهای خط قلمرو) رخ میدهند. بنابراین، میتوان (~D⊃E)⊃F را در سطر ۱۱ از (D∨E)⊃F در سطر ۲ با استفاده از استلزام مادی، و میتوان ~F⊃~A را در سطر ۱۲ از A⊃F، در سطر ۱۰ توسط ترانهش استنتاج کرد.
هنگام استفاده از روش برهان شرطی، هر مقدمهِ اصلی قلمرو نامحدود خود را تا پایان برهان نگاه میدارد. مقدمات اصلی ممکن است با مفروضات اضافی تکمیل شود، اما هر چنین فرضی، قلمرو محدودی خواهد داشت که تا پایان برهان گسترش نمییابد. نتیجهِ یک برهان شرطی، که از دنبالهِ استنتاجها درون یک برهان شرطی بهدست میآید، گزارهای است که از مقدمات استنتاج میشود، درست مانند گزارهای که مستقیماً از مقدمات، بدون هیچ گونه کاربرد C.P.، بهدست آمده باشد، برای مثال، (~D⊃E)⊃F فقط از مقدمات بهدست میآید، یعنی وقتی توسط استلزام مادی در سطر ۱۱ از (D∨E)⊃F و از سطر ۲ استنتاج شده است.
میتوان با تمرین به روش برهان شرطی به بهترین وجه چیره شد. هر چه شخص برهانهای بیشتری را با روش برهان شرطی به انجام رساند، آشکارا خواهد دید که چگونه در زمینههای مختلف میتواند از آن بهره گیرد.
به همین جهت، اکنون نمونههای دیگری از برهان شرطی (C.P.) را بررسی میکنیم، و طول و دشواری برهانها را با و بدون C.P. مقایسه میکنیم، ابتدا توجه داشته باشید که برهان استدلال بالا بهوسیله C.P. تنها به ۱۰ سطر نیاز دارد، حال آنکه با برهان خطی و فقط با نوزده قاعده استنتاج به ۲۰ سطر نیاز دارد.

ضرورت دارد تا بر قواعد نوزدهگانه چیرگی داشته باشید. چنین چیرگی شخص را توانا میکند تا حتی برهانهای بسیار دشوار را، با یا بدون .C.P، بکار گیرد. با این حال، وقتی برهان ۲۰ سطری بالا را با برهان شرطی ۱۰ سطری که قبلا ارائه شد مقایسه میکنیم، میبینیم که برهان شرطی نه تنها نصف طول دیگری است، بلکه برهان طولانیتر به سه کاربرد پخش پذیری نیاز دارد و نیز به نگاهی در لایهای ژرفتر که برهان شرطی به آن نیاز ندارد. هنگامی که گزاره A را در برهان شرطی فرض میگیریم، بلافاصله روند اجرای برهان شرطی را میتوان دید: با افزایش ممیتوان A∨B را استنتاج کرد، که به ما امکان میدهد C•D را استنتاج کنیم. جابجایی و ساده کرده C•D به D، کمک میکند تا D∨E را با افزایش استنتاج کنیم، و سپس تالی نتیجه شرطی، یعنی F، را توسط قیاس استثنایی استنتاج کنیم. روند برهان شرطی طبیعی است، به راحتی قابل درک و نمایش است، اما برهان ۲۰ سطری چنین نیست. برهان شرطی جایگزین چیرگی بر قواعد نوزده گانه نمیشود، اما پس از چیرگی به آن، افزودهای توانمند به جعبه ابزار منطقی ما خواهد بود.
در اینجا یک استدلال معتبر وجود دارد که برهان آن با قواعد نوزده گانه بسیار دشوار است و به ۱۸ سطر نیاز دارد.
(P۱): (H ⊃ P) • (S ⊃ W)
/∴ (H ∨ S) ⊃ (P ∨ W)

ولی با C.P برهان این استدلال بسیار آسان است و تنها در ۴ سطر قابل اجرا است!
| ۱. | (H ⊃ P) • (S ⊃ W) | /∴ (H ∨ S) ⊃ (P ∨ W) |
| ۲. | H ∨ S | /∴ P ∨ W (C.P فرض) |
| ۳. | P ∨ W | ۲, ۱, C.D. |
| ۴. | (H ∨ S) ⊃ (P ∨ W) | ۲ - ۳, C.P. |
اکنون، استدلال دیگری را در نظر بگیرید که بدون .C.P، تا اندازهای دشوار است.
(P۱): (L ⊃ H) • (Q ⊃ S)
/∴ (L • Q) ⊃ (H • S)
برهان این استدلال با قواعد نوزده گانه مستلزم ۱۷ سطر است.
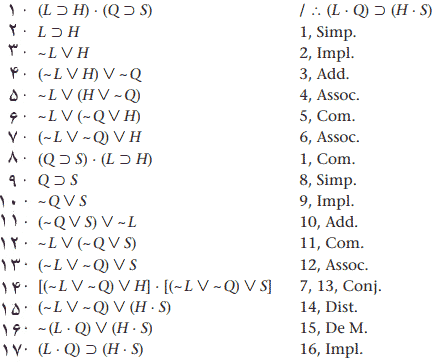
با C.P. ممیتوان این استدلال را در ۱۲ سطر به قرار زیر اثبات کرد.
| ۱. | (L ⊃ H) • (Q ⊃ S) | /∴ (L • Q) ⊃ (H • S) |
| ۲. | L • Q | /∴ H • S (C.P فرض) |
| ۳. | L | ۲, Simp. |
| ۴. | Q • L | ۲, Com. |
| ۵. | Q | ۴, Simp. |
| ۶. | L ⊃ H | ۱, Simp. |
| ۷. | H | ۶, ۳, M.P. |
| ۸. | (Q ⊃ S) • (L ⊃ H) | ۱, Com. |
| ۹. | Q ⊃ S | ۸, Simp. |
| ۱۰. | S | ۹, ۵, M.P. |
| ۱۱. | H • S | ۷, ۱۰, Conj. |
| ۱۲. | (L • Q) ⊃ (H • S) | ۲ - ۱۱, C.P |
باز هم، نه تنها برهان شرطی بطور قابل توجهی کوتاهتر از برهانی است که فقط از قواعد نوزدهگانه استفاده میکند، بلکه برهان شرطی نیز بسیار راحتتر اجرا میشود. به محض اینکه L•Q را فرض گرفتیم، خواهیم دید H را میتوان از L⊃H و L بهدست آورد، نیز S را میتوان از Q⊃S و Q بهدست آورد. H و S را میتوان به آسانی عطف کرد، تا تالی گزاره شرطی که دنبال آن بودیم را به ما بدهد.
ج. زیر-برهانهایِ شرطییِ تو در تو
قاعده برهان شرطی را میتوان درون یک برهان شرطی به کار برد، به قسمی که یک زیر-برهان شرطی (تودرتو) و خط قلمرو آن در حصار یک برهان شرطی و خط قلمرو آن باشد. برای مثال، برهان شرطی اعتبار برای استدلالِ
(P۱): A ⊃ (B ⊃ C)
(P۲): B ⊃ (C ⊃ D)
∴ A ⊃ (B ⊃ D) III استدلال
برهان اعتبار برای استدلال زیر نیز است؛
(P۱): A ⊃ (B ⊃ C)
(P۲): B ⊃ (C ⊃ D)
(P۳): A
∴ (B ⊃ D) IV استدلال
و از آنجا که دومی خود دارای نتیجه شرطی است، برای آن میتوان یک برهان شرطی بهوسیله اثبات اعتبار استدلال زیر
(P۱): A ⊃ (B ⊃ C)
(P۲): B ⊃ (C ⊃ D)
(P۳): A
(P۴): B
∴ D V استدلال
ارایه کرد.
اگر A⊃(B⊃D) بهطور معتبر از دو مقدمه اصلی برهان III بهدست آید، میتوان این را با فرض A و استنتاج B⊃D در یک برهان شرطی ثابت کرد. هنگامی که برهان شرطی اول را آغاز کردیم، میتوانیم B را به نوبت خود در یک زیر-برهان شرطیِ تودرتو نیز فرض بگیریم و ثابت کنیم که D بهطور معتبر بهدست میآید. این برهان شرطی دوگانه، متشکل از یک برهان شرطی اصلی و یک زیر-برهان C.P.، بهقرار آمده در زیر است.
| ۱. | A ⊃ (B ⊃ C) | ||
| ۲. | B ⊃ (C ⊃ D) | /∴ A ⊃ (B ⊃ D) | |
| ۳. | A | /∴ B ⊃ D (C.P فرض) | |
| ۴. | B | /∴ D (C.P فرض) | |
هر کاربردِ C.P. باید با خط قلمرو عمودی خود نشان داده شود. برای مثال، خط قلمرو عمودی در کنار فرض B، خودش در سمت راست خط قلمرو قرار دارد، که نشان میدهد که قلمرو برهان شرطی با فرض B، خود درون یک برهان شرطی (یا غیر مستقیم➥) متفاوت است.برهان غیرمستقیم را در همین فصل ببینید. هر برهان شرطی نیز در ستون توجیهی با کج-خط خود (/)، یعنی نشانه «بنابراین» (∴)، عبارت-گزارهای که باید از فرضِ گرفتهشده استنتاج شود، و «(فرض C.P.)» یا «(A.C.P.)» نشان داده میشود. برهان شرطی دوگانه کامل استدلال III در بالا، حاوی یک زیر-برهان C.P. تو در تو، به شرح زیر است.
| ۱. | A ⊃ (B ⊃ C) | ||
| ۲. | B ⊃ (C ⊃ D) | /∴ A ⊃ (B ⊃ D) | |
| ۳. | A | /∴ B ⊃ D (C.P فرض) | |
| ۴. | B | /∴ D (C.P فرض) | |
| ۵. | B ⊃ C | ۱, ۳, M.P. | |
| ۶. | C | ۵, ۴, M.P. | |
| ۷. | C ⊃ D | ۲, ۴, M.P. | |
| ۸. | D | ۷, ۶, M.P. | |
| ۹. | B ⊃ D | ۴ - ۸, C.P. | |
| ۱۰. | A ⊃ (B ⊃ D) | ۳ - ۹, C.P | |
در اجرای دومین برهان شرطی تودرتو، ما ثابت میکنیم که D بهطور معتبر از چهار مقدمه در استدلال V بهدست میآید. این اثبات نشان میدهد که استدلال IV معتبر است — یعنی، B⊃D بهطور معتبر از سه مقدمه استدلال IV بهدست میآید — با اثبات اینکه اگر دو مقدمه اصلی استدلال III درست باشند، و A نیز درست باشد، آنگاه اگر B (درست است) آنگاه D (درست است) (یعنی، B⊃D را به دنبال دارد). این برهان شرطی تودرتو اولین برهان شرطی را کامل میکند، زیرا ما ثابت کردهایم که اگر دو مقدمه اصلی درست باشند، و همچنین درستی عبارت-گزارهای A را فرض کنیم، آنگاه B⊃D بهطور معتبر بهدست خواهد آمد. برهان شرطی اصلی و زیر-برهان C.P. آن، اعتبار استدلال III را با اثبات اینکه A⊃(B⊃D) بهطور معتبر از دو فرض اصلی برهان C.P. بهدست میآید، اثبات میکند.
برهان این استدلال تنها با قواعد نوزده گانه نیز تنها ۱۰ سطر است، اما اجرای آن به آسانی اثبات شرطی نیست.
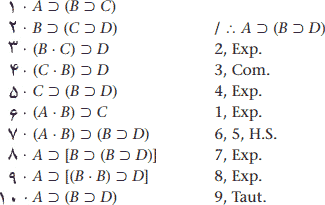
این دو برهان نشان میدهند که توان برهان شرطی تنها در کوتاه کردن برهان نیست. در اینجا دو برهان به یک اندازه هستند، اما، برهان دوم مستلزم نگاه ژرفتر یا پشتکار و چیرگی ویژه بر کارزدن واگردانی در هر دو جهت است، حال آنکه، برهان شرطی بسیار آشکارا است. هنگامی که شخص دو فرض را برای دو اثبات شرطی گرفت، چهار کاربرد خودکار قیاس استثنایی (M.P.) بعداً هر دو فرض را تخلیه و اثبات را تکمیل میکند.
مثال دیگری از استدلالی که میتوان اعتبار آن را با کاربردهای متعدد و تودرتوی برهان شرطی اثبات کرد، استدلال زیر است.
(P۱): [(D ∨ E) • F] ⊃ G
(P۲): (F ⊃ E) ⊃ (H ⊃ I)
(P۳): H
∴ D ⊃ I
اثبات این استدلال تنها با استفاده از قواعد نوزده گانه در ۱۶ سطر به قرار زیر قابل اجرا است:
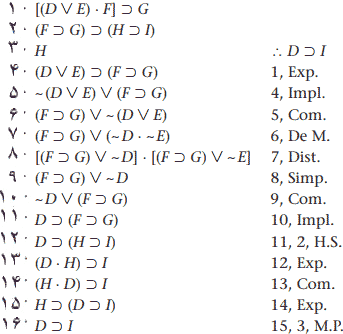
با این حال، با در دست داشتن C.P.، میتوانیم برهان را بسیار کارآمدتر اجرا کنیم. در واقع، اگر C.P. را آغاز کنیم و عبارت-گزارهای D را مقدمِ نتیجهیِ شرطی D⊃I فرض کنیم، بلافاصله میببینیم که گزاره مورد نظر، یعنی I، فقط در H⊃I به عنوان تالییِ یک شرطی رخ داده است. از آنجایی که ما H را به عنوان مقدمه داریم، اگر بتوانیم H⊃I را بهدست آوریم، میتوانیم I را با .M.P استنتاج کنیم. برای استنتاج H⊃I از مقدمه ۲ توسط M.P، ابتدا باید مقدم فرض دوم یعنی F⊃G را استخراج کنیم. برای این منظور، یک C.P. تودرتویِ دوم را با فرض مقدم F⊃G (یعنی، F) برقرار میکنیم.
لطفاً توجه داشته باشید: اکنون که سرشت یک فرضِ برهان شرطی را کاملاً درک کردهایم، از این پس از آن بجای «فرض، C.P»، از کوتاه شده آن با «.A.C.P» یاد خواهیم کرد.
| ۱. | [(D ∨ E) • F] ⊃ G | ||
| ۲. | (F ⊃ G) ⊃ (H ⊃ I) | ||
| ۳. | H | /∴ D ⊃ I | |
| ۴ | D | /∴ I (A.C.P.) | |
| ۵. | F | /∴ G (A.C.P.) | |
هنگامی F⊃G را با C.P. بهدست آوردیم، H⊃I را با .M.P استنتاج میکنیم و سپس عبارت I را از H⊃I و H را با .M.P بهدست میآوریم، بنابراین برهان شرطی اصلی خود را با نتیجه دلخواه، D⊃I، به پایان میبریم.
| ۱. | [(D ∨ E) • F] ⊃ G | ||
| ۲. | (F ⊃ G) ⊃ (H ⊃ I) | ||
| ۳. | H | /∴D⊃ I | |
| ۴. | D | /∴I (A.C.P.) | |
| ۵ | F | /∴G (A.C.P.) | |
| ۶. | D ∨ E | ۴ Add | |
| ۷. | (D ∨ E) • F | ۶, ۵, Conj. | |
| ۸. | G | ۷, ۱, M.P | |
| ۹. | F ⊃ G | ۵ - ۸, C.P | |
| ۱۰. | H ⊃ I | ۲, ۹, M.P. | |
| ۱۱. | I | ۱۰, ۳, M.P. | |
| ۱۲. | D ⊃ I | ۴ - ۱۱, C.P | |
این برهان توان C.P. را هنگامی که با درک محکمی از تکنیکِ برهان ترکیب شود نمایان میکند. در این مورد، توجه داریم که باید یک برهانِ شرطیِ تودرتویِ دومی را برقرار کنیم، زیرا متوجه عبارت-گزارهای مورد نیاز، یعنی I، در مقدمات شده بودیم.
د. برهان شرطی برای استدلالهایی که نتیجه آنها گزاره شرطی نیست
از برهان شرطی میتوان برای اثبات اعتبار همه استدلالهایی که نتیجه آنها گزارههای شرطی نیستند استفاده کرد. استدلالهایی که نتیجه آنها منطقاً همارز گزارههای شرطی است، نمونههای آشکاری هستند. دو استدلال زیر را در نظر بگیرید.
(P۱): (A ∨ B) ⊃ (C • D)
(P۲): (D ∨ E) ⊃ F
∴ ~A ∨ F
(P۱): (A ∨ B) ⊃ (C • D)
(P۲): (D ∨ E) ⊃ F
∴ ~(A • ~F)
از آنجایی که هر دو ~A∨F و ~(A•~F) منطقاً همارز A⊃F هستند، اثبات این استدلالها را میتوان با گسترش برهان ۱۰ سطری موجود در همین قسمت (ب) بالا، به ترتیب با یک و سه استنتاج ایجاد کرد. بنابراین، یک برهان برای استدلال اول بهقرار زیر است:
| ۱. | (A ∨ B) ⊃ (C • D) | |
| ۲. | (D ∨ E) ⊃ F | /∴ ~A ∨ F |
| ۳. | A | /∴ F (A.C.P) |
| ۴. | A ∨ B | ۳, Add. |
| ۵. | C • D | ۱, ۴, M.P. |
| ۶. | D • C | ۵, Com. |
| ۷. | D | ۶, Simp. |
| ۸. | D ∨ E | ۷, Add. |
| ۹. | F | ۲, ۸, M.P. |
| ۱۰. | A ⊃ F | ۳ - ۹, C.P. |
| ۱۱. | ~A ∨ F | ۱۰, Impl. |
و برهان استدلال دوم در بالا دقیقاً دو سطر طولانیتر است:
| ۱. | (A ∨ B) ⊃ (C • D) | |
| ۲. | (D ∨ E) ⊃ F | /∴ ~(A • ~~F) |
| ۳. | A | /∴ F (A.C.P) |
| ۴. | A ∨ B | ۳, Add. |
| ۵. | C • D | ۱, ۴, M.P. |
| ۶. | D • C | ۵, Com. |
| ۷. | D | ۶, Simp. |
| ۸. | D ∨ E | ۷, Add. |
| ۹. | F | ۲, ۸, M.P. |
| ۱۰. | A ⊃ F | ۳ - ۹, C.P. |
| ۱۱. | ~A ∨ F | ۱۰, Impl. |
| ۱۲. | ~A ∨ ~~F | ۱۱, D.N. |
| ۱۳. | ~(A • ~~F) | ۱۲, DeM. |
این دو برهان سودمندی و توان برهان شرطی را نشان میدهند. در هر نقطهای از برهان، اگر بخواهیم یک ترکیبِ فصلی یا نقیضِ ترکیب عطفی را استنتاج کنیم، میتوانیم برهان شرطی را برقرار کنیم. برای مثال، در آخرین استدلالی که دقیقاً در بالا ثابت شد، اگر همارزیهای منطقی، یعنی قواعد جایگزینی را بدانیم، بلافاصله خواهیم دانست که
~(A • ~~F)
با کارزدن نقض دوگانه و قضیه دمورگان همارز منطقیِ
~A ∨ F
است. و سرانجام آنکه ~A∨F توسط استلزام مادی منطقاً همارزِ
A ⊃ F
است. با تشخیص این همارزیهای منطقی، برهان شرطی را برای اثبات گزاره شرطی A⊃F ترقرار میکنیم، و پس از استنتاج معتبر، A⊃F عبارت ~A∨F را با استلزام مادی و سپس ~(A•~F) را با نقض دوگانه و قضیه دمورگان بهدست میآوریم.
به استدلال زیر نگاه کنید.
(P۱): (J ∨ A) ⊃ [(S ∨ K) ⊃ (~I ∨ Y)]
(P۲): (~I ∨ ~M) ⊃ E
∴ J ⊃ (~S ∨ E)
همانطور که برهان زیر نشان میدهد، این استدلال به آسانی قابل اثبات نیست.
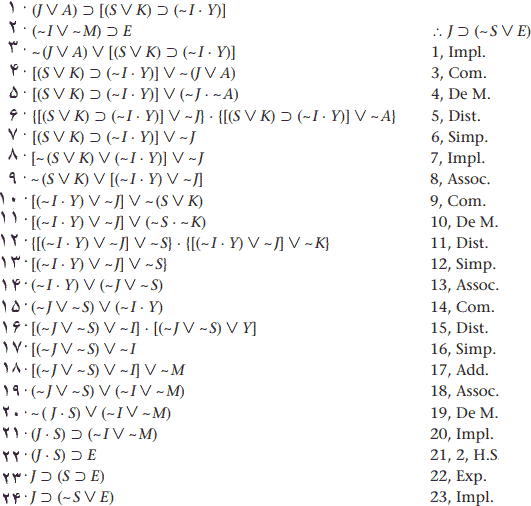
با این حال، برهان شرطی این استدلال بسیار راحتتر به انجام میرسد. یک بار در اجرای .C.P دیدیم که تالییِ نتیجهِ شرطی، ~S∨E است. اگر نتیجه J⊃(S⊃E) بود، بلافاصله به فکر انجام برهان شرطی دوگانه به قرار زیر میشدیم:
| ۱. | (J ∨ A) ⊃ [(S ∨ K) ⊃ (~I ∨ Y)] | ||
| ۲. | (~I ∨ ~M) ⊃ E | ∴ J ⊃ (~S ∨ E) | |
| ۳. | J | /∴ S ⊃ E (A.C.P.) | |
| ۴. | S | /∴ E (A.C.P.) | |
| ۵. | J ∨ A | ۱, Add.. | |
| ۶. | (S ∨ K) ⊃ (~I ∨ Y) | ۱, ۵, M.P. | |
| ۷. | S ∨ K | ۴, Add. | |
| ۸. | ~I ∨ Y | ۶, ۷, M.P. | |
| ۹. | ~I | ۸, Simp. | |
| ۱۰ | ~I ∨ ~M | ۹, Add. | |
| ۱۱ | E | ۲, ۱۰, M.P. | |
| ۱۲. | S ⊃ E | ۴ - ۱۱, C.P. | |
| ۱۳. | J ⊃ (S ⊃ E) | ۳ - ۱۲, C.P. | |
| ۱۴. | J ⊃ (~S ∨ E) | ۱۳, .Impl | |
هنگامی که ما E را در سطر ۱۱ توسط .M.P استنتاج کردیم، دومین فرض .C.P را تخلیه میکنیم و S⊃E را در سطر ۱۲ بهدست میآوریم. از آنجا که، S⊃E نتیجه اولین برهان شرطی ما است، بلافاصله اولین فرضِ .C.P را تخلیه و J⊃(S⊃E) را در سطر ۱۳ استنتاج میکنیم. به یاد آورید که ما برای اثبات، .C.P تودرتو را با آگاهی از اینکه J⊃(S⊃E) منطقاً همارز با J⊃(~S∨E) است آغاز کردیم. بنابراین، باید J⊃(~S∨E) را در سطر ۱۴ بهدست بیاوریم و سپس است که اثبات ما کامل است.
سرانجام، برهان شرطی در اثبات اعتبار استدلالهایی که نتایج آنها گزارههای دو شرطی هستند نیز بسیار مفید است. برای مثال، استدلال زیر یک نتیجه دو شرطی دارد.
(P۱): (C ∨ D) ⊃ (E ⊃ F)
(P۲): [E ⊃ (E • F)] ⊃ G
(P۳): G ⊃ [(~H ∨ ~~H) ⊃ (C • H)]
∴ C ≡ G
همانطور که میدانیم دوشرطی زیر
C ≡ G
منطقاً همارز با ترکیب عطفی دو گزاره شرطی است:
(C ⊃ G) • (G ⊃ C).
بنابراین، برای استنتاج دو شرطی میتوانیم دو گزاره شرطی را با دو برهان شرطی متوالی بهدست آوریم و سپس نتایج آنها را با استفاده از ترکیب عطفی به هم پیوند دهیم.
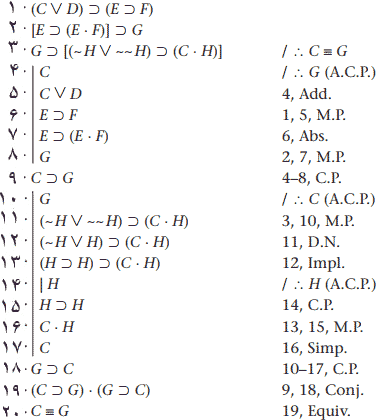
ساختار این برهان دربردارِ دو برهانِ شرطی مجزا و متوالی است، که در پی آن ترکیب عطفی نتیجههای آنها آمده است. توجه به این نکته ضروری است که استنتاج (C⊃G)•(G⊃C) در سطر ۱۹ محدودیتهای قلمرو را نقض نمیکند: C⊃G در سطر ۹ پس از یک برهان شرطی و G⊃C درسطر ۱۸ پس از دومین برهان شرطی اصلی استنتاج شده است. هنگامی که این دو عبارت شرطی در سطر ۱۹ به هم پیوستند، نتیجهِ استدلال، C≡G، در سطر ۲۰ با همارزی مادی بهدست آمده است.
آنطور که در این قسمت دیدیم، برهان شرطی یک افزونه قدرتمند و بسیار انعطاف پذیر به جعبه ابزار منطقی ما است. هنگامی که .C.P به قواعد نوزده گانه استنتاج اضافه شود، میتوانیم به راحتی و کارآمدی اعتبارِ انواعِ استدلال را اثبات کنیم. علاوه بر این، هر زمان که بخواهیم میتوانیم .C.P را برای استنتاج یک گزاره شرطی، یا به خاطر خود آن یا به منظور استنتاج یک دو شرطی، به کار بریم.
تمرین
برای اثبات اعتبار استدلالهای زیر از برهان شرطی استفاده کنید.

ه برهان شرطی برای توتولوژیها
از برهان شرطی نیز میتوان برای اثبات اینکه یک عبارت گزارهای یک توتولوژی است استفاده کرد. در این حالت، از آنجا که اعتبار یک «استدلال» مورد اثبات نیست، در واقع یک توتولوژی بدون آغاز از مقدمات مورد اثبات خواهد بود. در چنین حالتی، ما مقدم گزاره موردنظر را فرض میگیریم، تالی آن را استنتاج میکنیم و سرانجام توتولوژی شرطی را استنتاج میکنیم. در اثبات، از اینکه نتیجه باید درست باشد اگر مقدم درست است، استفاده کرده و ثابت میکنیم که گزاره شرطی یک توتولوژی است، زیرا نممیتواند نادرست باشد.
توتولوژی شرطی زیر را نگاه کنید.
(Q ⊃ R) ⊃ [(P ⊃ Q) ⊃ (P ⊃ R)]
این عبارت گزارهای با برهان شرطی زیر ثابت میشود.
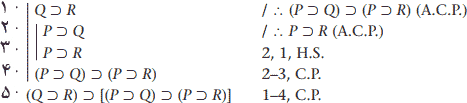
ما Q⊃R را در برهان شرطی اصلی فرض میکنیم، و بلافاصله P⊃Q را در یک زیر-برهان تودرتویِ .C.P دوم فرض میگیریم، زیرا P⊃Q مقدم تالیِ توتولوژیای است که باید اثبات شود. سپس P⊃R را با .H.S استنتاج میکنیم، فرض دوم را تخلیه میکنیم و با اندریافت زیر:
(P⊃Q)⊃(P⊃R)،
زیر-برهان شرطی را تمام میکنیم، سپس و بلافاصله اولین فرض اصلی را تخلیه میکنیم و
(Q⊃R)⊃[(P⊃Q)⊃(P⊃R)]
را توسط .C.P اندریافت میکنیم.
در بخش ۱۰.۱۴ (۶)، خواهیم دید که اثبات شرطی کارآمدترین روش برای اثبات توتولوژیهای شرطی است.
برهانی که در آن، گزارهای مانند p فرض گرفته میشود، سپس با کارزدن تعداد محدودی قواعد استنتاج، برخی گزاره مانند q استنتاج میشود، و در پایان، از طریق قاعده «اثبات شرطی (.C.P)»، گزاره اثباتشده «p⊃q» نتیجه گرفته میشود. (به عنوان مثال، اگر p، سپس q).
تمرین
برای اثبات اعتبار توتولوژیهای زیر از برهان شرطی استفاده کنید.